
Учебное пособие 2003
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
0 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
nv |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
-2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
- |
|
|
- |
|
|
|
- |
|
|
|
|
|
|
10 |
|
|||||||
-1 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
10 |
|
|
- |
|
|
|
- |
|
|
|
|
|
|
18 |
|
|||||||
0 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
32 |
|
|
3 |
|
|
|
9 |
|
|
|
|
|
|
44 |
|
|||||||
1 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
4 |
|
|
12 |
|
|
|
6 |
|
|
|
|
|
|
22 |
|
|||||||
2 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
- |
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nu |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
46 |
|
|
16 |
|
|
|
20 |
|
|
|
|
|
n = 100 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2. Найдем U иV : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ( |
2) |
|
14 ( |
1) |
46 0 |
16 1 |
|
20 2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
U |
|
|
|
|
|
|
0,34 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
10 ( |
|
2) |
|
|
18 ( |
1) |
44 0 |
22 1 |
6 2 |
|
|
0,04 . |
|
||||||||||||||||||||
|
|
|
|
V |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 : |
|
|
|
||||||||||||||||||||||||
3. Найдем вспомогательные величины U |
2 |
иV |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n U 2 |
4 4 14 1 46 0 16 1 20 4 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
U 2 |
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 26 |
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n V 2 |
10 4 18 1 44 0 22 1 6 4 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
V 2 |
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 04 . |
|
||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. Найдем |
|
U |
и |
V : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
U 2 |
|
|
(0, 34)2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
U |
|
|
|
|
|
U |
1, 26 |
1, 07 ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0, 04 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
V |
|
|
|
|
|
|
|
V |
1, 04 |
1, 02 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
|
|
Составляем |
расчетную таблицу |
для |
|
нахождения |
|||||||||||||||||||||||||||||||||||||
nUV |
UV по следующей схеме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
а) в каждой клетке, в которой частота nUV |
0 , записывают |
|||||||||||||||||||||||||||||||||||||||||||
в правом верхнем углу произведение частоты nUV |
|
на варианту |
||||||||||||||||||||||||||||||||||||||||||
U. Например, в правых верхних углах клеток первой строки |
||||||||||||||||||||||||||||||||||||||||||||
записаны произведения: 4 ( |
2) |
8 ; 6 ( 1) |
|
6 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
171 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

б) складываем все числа, помещенные в правых верхних углах клеток одной строки, и их сумму записываем в клетку
этой же |
строки-столбца V. Например, для первой |
строки:V |
8 ( 6) 14 . |
в) умножаем варианту V на U и полученное произведение записываем в последнюю клетку той же строки, то есть в клетку столбца VU. Например, в первой строке таблицы V = -2,
U = -14, следовательно,VU |
( 2) ( 14) 28. |
|
|
||||||||||
г) наконец, сложив все числа столбца VU, получаем |
|||||||||||||
сумму VU , которая равна |
искомой |
сумме |
nUV |
UV . |
|||||||||
Например, |
для |
данной |
таблицы |
имеем |
VU |
82 , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
следовательно, nUV |
UV |
|
82 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
V |
|
-2 |
|
-1 |
|
0 |
|
1 |
2 |
U |
nUV U |
VU |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
-6 |
|
|
|
|
|
|
|
|
|
-2 |
|
|
6 |
|
- |
|
- |
- |
|
-14 |
28 |
||
|
4 |
|
|
|
|
||||||||
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
0 |
|
|
|
|
|
|
|
-1 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
- |
|
8 |
|
|
- |
- |
|
-8 |
|
8 |
||
|
|
|
|
- |
|
|
|
||||||
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
- |
|
- |
|
0 |
|
3 |
18 |
|
21 |
|
0 |
|
|
|
32 |
|
3 |
9 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
1 |
|
- |
|
- |
|
0 |
|
12 |
12 |
|
24 |
24 |
|
|
|
|
|
|
|
4 |
|
12 |
6 |
|
|
|
|
172

|
|
|
|
|
4 |
12 |
6 |
|
|
|
|
2 |
|
- |
- |
- |
1 |
10 |
11 |
|
22 |
|
|
1 |
5 |
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
10 |
|
|
|
V |
nUV |
V |
|
- |
|
|
|
|
|
VU 82 |
-8 |
-6 |
14 |
16 |
|
|
V |
||||
20 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UV 82 |
|
↑ |
|
UV |
|
16 |
20 |
0 |
14 |
32 |
|
← |
|
|
|
V |
|
контроль |
||||||
|
|
|
|
|
|
|
|
|
||
|
Для |
контроля |
расчета |
аналогичные |
вычисления |
|||||
производят по столбцам: произведения nUV V записывают в
левый нижний угол клетки, содержащей частоту; все числа, помещенные в левых нижних углах одного столбца, складывают и их сумму помещают в «строку V»; наконец, умножают каждую варианту U на V и результат записывают в клетках последней строки. Сложив все числа последней
строки, получают сумму UV , которая также равна искомой
U
сумме |
nUV UV . |
Например, |
для данной таблицы UV 82 , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
U |
следовательно, |
nUV UV |
82 . |
|
|
||||||||
6. Находим искомый выборочный коэффициент |
||||||||||||
корреляции: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rв |
nUV |
UV |
nUV |
|
|
82 100 0, 34 0, 04 |
0, 76 . |
||||
|
|
n |
U V |
|
|
|
|
100 1, 07 1, 02 |
||||
|
|
|
|
|
|
|
|
|||||
Итак rb |
0, 76 . |
|
|
|
|
|
|
|
|
|
|
|
После того, как разобрали метод вычисления выборочного коэффициента корреляции, приведем пример на отыскание уравнения прямой линии регрессии.
Пример 3. Найти выборочное уравнение прямой линии Y на X по данным корреляционной таблицы.
173
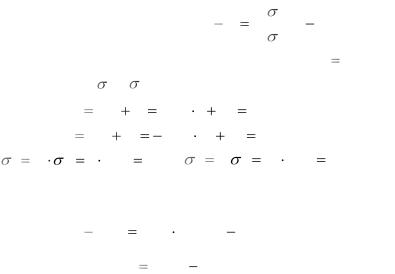
Искомое уравнение имеет вид: y |
|
y |
|
r |
|
y |
(x x ) . (*) |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
в |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент корреляции rв уже |
вычислен: rв |
0, 76 . |
||||||||||||||
Остается найти x , |
y , x |
и y : |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
31,70 ; |
|
|||||
|
x Uh1 |
c1 |
0,34 5 |
30 |
|
|
||||||||||
|
|
|
|
|
|
|
35,60 ; |
|
||||||||
y |
Vh2 |
c2 |
0,04 10 |
36 |
|
|||||||||||
x h1 U |
5 1, 07 |
5, 35 ; y |
|
h2 |
V |
|
10 1,02 |
10, 2 . |
||||||||
Подставляя найденные величины в уравнение (*), получим искомое уравнение прямой линии регрессии Y на X:
yx 35, 6 |
0, 76 |
10, 2 |
(x 31, 7) или |
||
|
5,35 |
||||
|
|
|
|||
yx |
1, 45x 10, 36 . |
||||
Вопросы для самопроверки.
1.В чем состоит различие между функциональной и статистической зависимостью между двумя переменными? Какую зависимость называют корреляционной?
2.Что называется уравнением регрессии Y на X? Напишите выборочное уравнение прямой линии регрессии Y на X?
3.Перечислите свойства выборочного коэффициента корреляции. Как найти этот коэффициент?
Содержание задания.
1. Усвоить различие между функциональной и статистической зависимостью между двумя переменными. Корреляционная зависимость.
2.Разобрать уравнение регрессии Y на X, написать выборочное уравнение прямой линии регрессии Y на X.
3.Научиться находить выборочный коэффициент корреляции. Изучить его свойства.
174

4. Дана корреляционная таблица с результатами измерений предела текучести X и предела прочности Y 60 марок стали.
|
|
|
|
xi (кг/мм2) |
|
|
|
|
yj |
|
|
|
|
|
|
|
|
(кг/мм2) |
|
|
|
|
|
|
|
|
60 |
5 |
|
|
|
|
|
|
5 |
80 |
3 |
3 |
4 |
|
|
|
|
10 |
100 |
|
1 |
7 |
6 |
|
|
|
14 |
120 |
|
|
1 |
8 |
4 |
|
|
13 |
140 |
|
|
1 |
1 |
5 |
2 |
|
9 |
160 |
|
|
|
|
|
5 |
2 |
5 |
180 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
||
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
8 |
4 |
13 |
15 |
9 |
7 |
4 |
n = 60 |
Определить меру линейной зависимости между пределом текучести и пределом прочности стали, то есть вычислить коэффициент корреляции.
5. Решить задачи [5], № 536 (а, б)
Тема 5.
Построение законов распределения.
Литература [2], стр. 245-252, 333
1. Выравнивание частот.
Пусть имеется генеральная совокупность, в ней изучается случайная величина Х выборочным методом. Взята выборка объема n:
xi |
x1 |
x2 |
… |
xk |
k |
|
ni n . |
||||||
ni |
n1 |
n2 |
… |
nk |
||
i 1 |
||||||
|
|
|
175 |
|
||

называются эмпирическими частотами – это фактически наблюдаемые частоты.
Рассмотрим два случая:
1) Случайная величина Х является дискретной величиной. Будем предполагать, что закон распределения случайной величины Х известен: значения xi случайная величина Х принимает с вероятностью pi, i=1, 2,…, k. В силу закона больших чисел при больших n относительные частоты
ni/n появления значения xi |
с большой |
вероятностью |
|||||||
приблизительно равны соответствующим pi: |
|
|
|||||||
|
|
|
|
|
ni |
|
pi . |
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
||
Введем числа ni', для которых будет выполняться строгое |
|||||||||
равенство |
ni |
' |
pi или ni' = npi. |
|
|
|
|||
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Числа |
|
ni' |
называют |
теоретическими |
или |
||||
выравнивающими частотами. |
|
|
|
||||||
Эмпирические |
и теоретические частоты |
должны |
быть |
||||||
близки, если закон распределения случайной величины Х отгадан правильно.
Выравниванием частот называется процесс замены эмпирических частот теоретическими.
Пример. Измерялась некоторая величина Х, в результате чего имеется выборка
xi |
0 |
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
ni |
120 |
|
167 |
|
130 |
69 |
27 |
5 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
объема n |
ni 520 . |
|
|
|
|
|
|
|||
|
i |
0 |
|
|
|
|
|
|
|
|
Предположим, что случайная величина Х подчиняется закону Пуассона. Найдем выравнивающие частоты при этом
предположении
176

ni' = npi.
Вероятности pi находим по закону Пуассона
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
e |
, i |
0, |
1, |
..., |
7 , |
||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
i! |
|
|
|
|
|
|
|
|
где |
M X |
xB - выборочное среднее. |
|
|
||||||||||
|
По выборке находим |
|
|
1 |
|
7 |
|
|
. |
|||||
|
xB |
|
|
|
ni xi |
1,5 |
||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n i 0 |
|
|
|
||
|
|
1,5 |
i |
|
|
|
|
|
|
|
|
|
||
|
Тогда p |
|
|
e 1,5 , |
i |
0, 1, |
..., |
7 . |
|
|
||||
|
|
|
|
|
||||||||||
|
i |
i! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти значения находятся по таблице. Выравнивающие частоты после округления можно принять равными
n0' = 116; n1' = 174; n2' = 131; n3' = 65; n4' = 25; n5' = 7; n6' = 2; n7' = 0.
Близость выравнивающих и эмпирических частот говорит в пользу предположения о верности распределения по закону Пуассона.
2) Пусть случайная величина Х является непрерывной величиной. В этом случае вероятности появления отдельных значений равны нулю. Поступаем следующим образом: интервал, на который попадают все значения случайной величины, делят на конечное число s непересекающихся частичных интервалов. Вычисляют вероятности pi попадания значений случайной величины Х в i-тый частичный интервал, а затем, как и для дискретного распределения, умножают объем выборки n на эти вероятности и получают выравнивающие частоты.
Таким образом, выравнивающие или теоретические частоты ni' для непрерывно распределенной случайной величины вычисляется по формуле:
ni' = npi, i=1, 2,…, s,
где n – объем выборки, pi – вероятность попадания случайной величины Х в i-тый интервал, вычисленная в предположении, что Х имеет предполагаемое распределение.
177

Пусть f(x) – плотность предполагаемого распределения случайной величины Х. Тогда вероятность попадания значений случайной величины Х в i-тый частичный интервал с использованием теоремы о среднем для определенного интеграла, определяется следующим образом:
|
xi |
hi |
|
|
|
|
|
|
|
2 |
|
hi |
|
hi |
|
|
|
|
|
|
|
|
|
|||
pi |
|
|
f x dx f xi xi |
xi |
f xi |
hi |
||
|
|
2 |
2 |
|||||
|
xi |
hi |
|
|
|
|||
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, pi |
|
f xi hi , а следовательно, ni ' |
npi nhi f |
xi . |
||||
Выравнивающие частоты можно выразить так же через функцию распределения случайной величины F(x). Если
обозначим i-тый интервал xi , xi 1 , |
то pi F xi 1 F xi , |
откуда следует, что ni ' n F xi 1 F |
xi . |
2. Построение кривой нормального вида по эмпирическим данным.
Пусть нормальная величина Х подчиняется нормальному закону распределения, тогда плотность распределения имеет вид
|
|
|
1 |
|
|
|
x |
a 2 |
|
||
|
f |
x |
|
|
e 2 |
2 . |
|||||
|
|
|
|
|
|
||||||
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
Параметры |
и |
a |
нам |
неизвестны, заменим их |
|||||||
статистическими оценками: математическое ожидание a выборочной средней xв , среднее квадратическое отклонение 
исправленным |
выборочным |
|
|
|
средним |
квадратическим |
||||||||
отклонением S': a |
xB , |
|
|
S '. |
|
|
|
|
|
|
||||
Величины xв |
и S' |
найдем по данным выборки. Тогда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
x xB |
|
|
|
|||
f x |
|
|
|
|
e |
2S 2 |
|
, и, следовательно, |
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
S |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
178 |
|
|
|
|
|||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nhi |
|
|
|
xi |
|
xB |
|
|
|
|||||
|
ni |
' |
|
nhi |
f |
xi |
|
|
|
|
|
|
|
|
l |
|
2 S 2 |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
S |
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Чтобы |
|
|
|
для |
|
|
подсчета |
|
|
|
|
воспользоваться |
||||||||||||||||||||
|
|
|
1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
xB |
|
|
|
|
|||||
функцией |
x |
|
|
l 2 |
, сделаем замену: |
|
|
|
t |
. Тогда |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
nhi |
|
1 |
|
|
|
|
t 2 |
|
|
nhi |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ' |
|
|
|
|
|
|
|
|
|
e 2 |
|
|
|
|
|
|
t |
i |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i |
|
|
|
S |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для |
функций |
|
|
|
x |
|
|
имеются |
|
|
таблицы. |
Можно |
||||||||||||||||||||
воспользоваться формулой, выражающей выравнивающие частоты через функцию распределения:
|
|
|
|
|
ni ' n Ф t2i Ф t1i |
, |
|
где t |
|
x1i xB |
, t |
|
x2i xB |
. |
|
1i |
|
|
|
2i |
|
||
|
|
|
|||||
|
|
Ф(х) – функция Лапласа, значения которой находят по |
|||||
|
|
|
|
|
|
таблице. |
|
|
Вычислив выравнивающие частоты |
ni', строят точки с |
|||||
координатами (xi, ni'), где xi – середина i-го интервала разбиения.
Содержание задания
1.Разобрать понятия:
а) эмпирических частот; б) выравнивающих (теоретических частот
дискретного распределения); в) выравнивающих частот непрерывного
распределения.
2.Разобрать методику вычисления теоретических частот нормального распределения.
3.Научиться строить нормальную кривую по опытным данным.
4.Научиться проводить оценку отклонения эмпирического распределения от нормального.
179
Заключение
Содержание и стиль изложения пособия определялись с точки зрения их практических приложений в различных областях инженерной практики. Ряд приведенных задач и примеров ориентирован на дальнейшее изучение вероятностных дисциплин, таких, как теория случайных процессов, математическая теория надежности и т.д. Применяемый в пособии математический аппарат основан на втузовском курсе высшей математики и не использует сложных понятий функционального анализа, теории меры, интеграла Лебега. Тем не менее принят современный способ изложения теории вероятностей на основе введения пространства элементарных событий и системы аксиом А.Н.Колмогорова. Однако аксиомы вводятся лишь после рассмотрения классического, геометрического и статистического определений как естественное распространение получающихся при таких определениях свойств вероятностей случайных событий
Основное внимание авторы уделяют не строгим формальным доказательствам, а единству методического подхода, иллюстрируемого многочисленными приложениями. Дополнение пособия рекомендациями для самостоятельного изучения пяти тем не вошедших в пособие, позволит организовать глубокое всестороннее изучение курса. Именно такой подход к изучению теории вероятностей и математической статистики более всего полезен тем, кто ставит перед собой цель решение конкретных задач.
Библиографический список
1. Румшиский Л.З. Элементы теории вероятностей. М., 1976. 234 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.,1977.
180
