
Учебное пособие 2003
.pdf
|
p11 |
p12 ... |
p1l |
|
|
P = |
p21 |
p22 ... |
p2l |
, |
|
... ... ... ... |
|||||
|
|
||||
|
pl1 |
pl 2 ... |
pll |
|
|
составленной из вероятностей перехода, которую называют матрицей перехода. Отметим, каким условиям должны удовлетворять элементы матрицы перехода.
Прежде всего как вероятности они должны быть неотрицательными числами, то есть при всех i и j
0≤pij≤1.
Далее, из того, что при переходе из состояния ei система переходит в одно и только одно из состояний еj (j=1,2,...,l), следует равенство
l
pij 1 |
i 1, 2,...,l , |
i
то есть сумма элементов каждой строки матрицы перехода равна единице.
Первая задача, которую нам надо решать для теории цепей Маркова, состоит в определении вероятности того, что система через п шагов будет находиться в состоянии еj, если ранее она находилась в состоянии ei. Обозначим эту вероятность через pij(п).
Через п-1 шагов система обязательно будет находиться в одном из состояний ek (k=1,2,...,l), причем в еk она будет c вероятностью pik(n-1). После этого за оставшийся шаг из состояния п-1 она перейдет в состояние j c вероятностью pkj(1). Используя формулу полной вероятности, получаем
|
e |
|
pij n |
pik n 1 pkj (1), pkj (1) pkj . |
(1) |
k |
1 |
|
Формула (1) называется равенством Маркова. Легко видеть, что матрица P (n) , составленная из чисел pij(п), равна
произведению матрицы составленной из чисел pij(п-1) на матрицу P , составленную из чисел pij ; иными словами
121

P (n) P (n 1) P = P n-1 P = P n .
Это означает, что вероятности pij(п) образуют матрицу, равную п –ой степени матрицы P . В частности, при п =2, имеем
P (2) P (1) P = P 2 .
Пример. Задача о стопке книг.
На столе лежит стопка книг. Если обозначить каждую книгу соответствующим номером, то порядок их расположения сверху вниз можно описать перестановкой из m чисел (i1, i2,…, im), где i1 - номер книги, лежащей сверху, i2 - номер следующей и так далее, im - номер книги, лежащей в самом низу. Предположим, что каждая книга берется с определенной вероятностью, скажем, книга c номером k берется c вероятноcтью pk (k=1,2,…,m), причем при возвращении она кладется сверху.
Возьмем произвольное cоcтояние (i1, i2,…, im). На следующем шаге оно либо остается неизменным, что происходит с вероятностью pii при выборе лежащей сверху книги с номером i1, либо меняется на одно из т-1 состояний вида (ik, i1,…, im), что происходит c вероятностью pik при
выборе книги с номером ik. Перед нами |
цепь Маркова с |
|||
соcтояниями, |
каждое |
из |
которых |
описывается |
соответствующей перестановкой (i1, i2,…, im) и указанными переходными вероятностями.
Остановимся на случае двух книг (т=2). Тогда имеются лишь два состояния е1=(1,2) и е2=(2,1).
Переходные вероятности имеют вид
p 11=p21=α, p12=p22=β, α+β=1
и матрица переходных вероятностей есть
P .
Вероятности перехода за два шага
p11(2)=p21(2)=α·α+β·α=α(α+β)=α, p 12(2)=p22(2)=α·β+β·β=β(α+β)=β,
122

P (2) |
p11 |
2 |
p12 |
2 |
. |
|
p21 |
2 |
p22 |
2 |
|||
|
|
|||||
Видно, что P (2) |
P 2 |
P |
|
и вообще в этом случае |
||
P (n) = P .
14. 2. Теорема о предельных вероятностях
Состояние еj. называется достижимым из еj, если за некоторое число m шагов система с положительной вероятностью переходит из еi в еj, то есть pij(m)>0 при некотором т.
Рассмотрим цепь Маркова с конечным чиcлом состояний e1, e2, …,em, каждое из которых достижимо из любого другого состояния. Более того, предположим, что существует такие п шагов, что система с положительной вероятностью может перейти из каждого состояния ei в любое другое состояние еj, то есть
min pij n |
0 . |
(2) |
i, j |
|
|
Теорема. Если при некотором l>0 все элементы матрицы перехода Pl положительны, то существуют такие постоянные
числа p j j |
1, 2,...,l |
, что независимо от индекса i имеют место |
равенства |
lim pij n |
p j , j 1, 2,3,..., m . |
|
n |
|
Теорема принимается без доказательства. Теорема о предельных вероятностях утверждает, что при выполнении условий теоремы вероятность того, что система находится в некотором состоянии ej, практически не зависит от того, в каком состоянии она находилась в далеком прошлом.
Предельные (финальные) вероятности p j , j 1,2,...,m являются решением следующей системы линейных уравнений:
|
m |
|
m |
p j |
pk pkj , |
j 1, 2,3,..., m. |
p j 1 |
|
k 1 |
|
j 1 |
|
|
123 |
|

Эти уравнения получаются, если в формуле (1) перейти к пределу при п→∞.
14.3. Стационарное распределение
Рассмотрим произвольную цепь Маркова с состояниями
е1, е2,… и числа |
p0 |
, i=1,2,..., такие, что p0 |
0 , |
p0 |
1, |
|||
|
|
i |
|
|
i |
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
p0 |
p0 p |
, j=1, 2,…. |
|
|
|
|
|
|
j |
i 0 j |
|
|
|
|
Взяв p0 |
, |
i=1,2,... в качестве начального распределения |
||||||
i |
|
|
|
|
|
|
|
|
вероятностей, получим следующие вероятности pj(n) для нахождения в соответствующих состояниях е через п шагов:
p |
j |
1 |
p0 p |
p0 , |
p |
j |
2 |
|
p 1 p |
p0 . |
||
|
|
i |
ij |
j |
|
|
|
i |
ij |
j |
||
|
|
|
i |
|
|
|
|
|
i |
|
|
|
Видно, что вероятности |
p j |
n |
p0j |
, |
j 1, 2,.... |
|||||||
Цепь Маркова называется стационарной, если |
||||||||||||
вероятности рj(п), j |
1, 2,...остаются неизменными при всех |
|||||||||||
п=1,2,3,... . |
|
|
|
|
|
|
|
|
|
|
|
|
Стационарными |
называются |
и |
соответствующие |
|||||||||
распределения |
вероятности p0j |
|
n , |
j |
1, 2,... . |
Согласно |
||||||
формуле (1) |
распределение |
вероятности |
pj , |
j 1, 2,... |
||||||||
является стационарным тогда и только тогда, когда оно удовлетворяет системе уравнений (3).
Если при любом начальном распределении существуют одни и те же предельные вероятности p j , то стационарное распределение единственно:
|
p0j p j , j |
1, 2,... . |
|
Обобщая |
полученные |
результаты, |
можно |
сформулировать следующее утверждение. |
|
||
При условии min pij n |
0 предельные вероятности |
||
|
i, j |
|
|
p j , j 1, 2,3,..., m |
являются |
единственным |
решением |
|
124 |
|
|

системы линейных уравнений (2), удовлетворяющим дополнительному требованию вида
p j 0, |
p j 1, |
|
j 1 |
и образуют стационарное распределение вероятностей. Пример. Задача о стопке книг (m=2). Как показывают
проведенные ранее расчеты стационарное распределение вероятностей возникает уже на первом шаге p1(n)=α , р2(п)=β при всех п=1,2,... и любом начальном распределении вероятностей.
15. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
15.1. Основные определения
Математической статистикой называется наука,
которая основывается на методах теории вероятностей, занимается систематизацией, обработкой и использованием экспериментальных данных для получения научных и практических выводов.
Одним из основных методов исследования случайных явлений в математической статистике является выборочный метод. Рассмотрим основные понятия этого метода.
Пусть рассматривается некоторый случайный эксперимент £, связанный с СВ X, имеющей ФР F(х). Полный набор всех возможных результатов измерений СВ X в
эксперименте £ называют генеральной совокупностью с ФР
F(х).
Число членов n, образующих генеральную совокупность, называют объемом генеральной совокупности.
Отметим, что объем генеральной совокупности может быть как конечным, так и бесконечным.
Выборкой (выборочной совокупностью (ВС)) объемом п из N генеральной совокупности (ГС) называется последовательность х1,х2,...,хп наблюдаемых значений СВ X,
125

соответствующих п независимым повторениям эксперимента
£.
Аналогично определяется выборка в случае, когда случайный эксперимент £ связан с несколькими СВ. Например, выборка объемом п из ГС с ФР F(х,у) есть последовательность (х1,y1),(x2,у2),…,(xn,уn) пар значений СВ X и Y, принимаемых ими в п независимых повторениях случайного эксперимента £.
Метод, состоящий в том, что на основании изучения характеристик и свойств выборки х1,х2,...,хп даются заключения о числовых характеристиках и законе распределения СВ X, называется выборочным методом. Выборка может быть записана в виде вариационного ряда или в виде статистического ряда.
Вариационным рядом выборки х1,х2,...,хп называется способ ее записи, при котором элементы xi упорядочиваются
по величине, то есть записываются в виде последовательности
х1,х2,...,хп , причем х1≤х2≤...≤хп.
Разность между максимальным и минимальным элементами выборки хп-х1=ω называется размахом выборки.
Пусть в выборке объемом п элементр xi встречается ni раз. Число ni называется частотой элемента xi. Очевидно, что
k
nni .
i1
Статистическим рядом называется последовательность пар (xi,ni), которая записываетоя обычно в виде таблицы
xi |
|
x1 |
x2 |
… |
xk |
ni |
|
n1 |
n2 |
… |
nk |
k |
|
|
|
|
|
ni |
n . |
|
|
|
|
i 1 |
|
|
|
|
|
Отношение ωi=ni/n называется относительной частотой, или частностью элемента xi выборки.
Статистическим распределением СВ X называется последовательность пар (x,ni/n), которая также записывается в
126

виде таблицы
xi |
x1 |
|
x2 |
|
… |
|
xk |
|
||||
|
ni |
n |
|
n |
|
|
… |
|
n |
|
|
|
ωi= n |
n |
|
n |
|
|
n |
|
|||||
|
|
|
1 |
|
|
2 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
||
k |
k |
|
|
|
|
|
|
|
|
|
||
ni / n 1 |
i |
|
|
|
|
|
|
|
|
|
||
i 1 |
i 1 |
|
|
|
|
|
|
|
|
|
||
Пример. Дана выборка из некоторой ГС
11,15,12,9,13,12,6,11,12,13,15,8,9,14,9,11,6. Определить объем,
размах выборки, а также построить вариационный и статистический ряды.
Решение. Объем п=17.Вариационный ряд 6,6,8,9,9,11,11, 11,12,12,12,13,13,14,15,15. Размах ω=12-6=6.
Статистический ряд и статистическое распределение имеют вид
xi |
6 |
|
8 |
9 |
|
11 |
12 |
13 |
14 |
15 |
n |
2 |
|
1 |
3 |
|
3 |
3 |
2 |
1 |
2 |
ωi |
2/17 |
|
1/17 |
3/17 |
|
3/17 |
3/17 |
2/17 |
1/17 |
2/17 |
|
ni |
n; |
|
i |
1 |
|
|
|
|
|
При большом объеме выборки ее элементы объединяют в группы (разряды), представляя результаты опытов в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки, разбивается на k частичных непересекающихся интервалов.
Обычно выбирают частичные интервалы одинаковой длины b=ω/k. После того, как частичные интервалы выбраны,
определяют частоты -количество ni элементов выборки,
попавших в i-тый интервал (элемент, совпадающий c верхней границей интервала, относится к следующему интервалу ). В группированный статистический ряд в верхнюю cтроку
записываются середины xi интервалов группировки, а в нижний - частоты ni .
127

В зависимости от объема выборки число k интервалов группировки берется от 6 до 20. Наряду с частотами ni удобно
одновременно |
подсчитывать |
также |
накопленные |
|||
i |
|
|
|
|
|
|
частоты |
nj |
, относительные частоты и накопленные |
||||
j |
1 |
|
|
|
|
|
|
|
i |
|
|
|
|
относительные частоты |
j |
, |
i 1, 2,..., k . |
|
||
|
|
|
|
|
|
|
|
|
j |
1 |
|
|
|
Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки.
Следует отметить, что группировка выборки вносит погрешность в последующие вычисления, которая становится
тем больше, чем меньше выбирается число интервалов. |
|
||||||||
Пример. Время решений контрольной работы |
|||||||||
студентами 2-го курса дается выборкой |
|
|
|
|
|||||
38 |
60 |
41 |
51 |
33 |
42 |
45 |
21 |
53 |
60 |
68 |
52 |
47 |
46 |
49 |
49 |
10 |
57 |
54 |
59 |
79 |
47 |
28 |
48 |
58 |
32 |
42 |
58 |
61 |
30 |
61 |
35 |
47 |
72 |
41 |
45 |
44 |
55 |
30 |
40 |
67 |
65 |
39 |
48 |
43 |
60 |
54 |
42 |
59 |
50 |
|
Построить выборку в виде таблицы частот |
||||||||||
группированной |
выборки, |
используя |
7 |
интервалов |
|||||||
группировки. |
|
|
|
|
|
|
|
|
|
||
|
Решение. Размах выборки 79-10=69. Длина интервала |
||||||||||
b=69/7 |
10. |
|
|
|
|
|
|
|
|
|
|
Инт. |
|
[10- |
[20- |
[30- |
[40- |
[50- |
[60- |
[70- |
|
|
|
|
20[ |
30[ |
40[ |
50[ |
6-[ |
70[ |
80[ |
|
|
|
|
|
|
|
|
|
|||||||
xi |
|
15 |
25 |
35 |
45 |
55 |
65 |
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
1 |
2 |
7 |
18 |
12 |
8 |
2 |
ni 50 |
|
|
ni |
|
1 |
3 |
10 |
28 |
40 |
48 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
0,02 |
0,04 |
0,14 |
0,36 |
0,24 |
0,16 |
0,04 |
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
0,02 |
0,06 |
0,20 |
0,56 |
0,80 |
0,96 |
1,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
128 |
|
|
|
|
|
|

15.2. Графическое представление выборки
Для наглядности сгруппированные статистические ряды представляются графиками и диаграммами.
Полигоном частот группированной выборки называется ломаная с вершинами в точках ( xi , ni ), i=1, 2,...,k.
Полигоном относительных частот группированной выборки называется ломаная с вершинами в точках ( xi , i ).
Гистограммой частот группированной выборки называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах так, что
площадь каждого прямоугольника равна частоте ni , i=1, 2,...,k.
Отсюда следует, что площадь гистограммы частот равна объему выборки п. В том случае, когда длины всех интервалов
одинаковы |
и |
равны b, |
высоты |
прямоугольников |
|||
равны hi |
ni / b , i=1, 2,...,k. Аналогично строится гистограмма |
||||||
относительных |
частот. |
Площадь |
гистограммы |
||||
относительных частот равна единице. |
|
|
|
||||
Полигоном |
накопленных |
частот |
группированной |
||||
выборки |
называется |
ломаная |
с |
вершинами |
в точках |
||
i |
|
|
|
|
|
|
|
( xi b / 2; |
nj ). |
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
Полигоном |
относительных |
накопленных |
частот |
||||
(кумулятивной кривой, кумулятой) называется ломаная с |
|||||||
|
|
|
|
i |
|
|
|
вершинами в точках ( xi |
b / 2; ( |
nj ) / n ). |
|
|
|||
|
|
|
j |
1 |
|
|
|
Замечание. Перечисленные графические представления аналогичным образом определяются и в случае негруппированной выборки.
Пример. Для выборки примера 2 построить гистограмму, полигон частот и кумулятивную кривую.
129
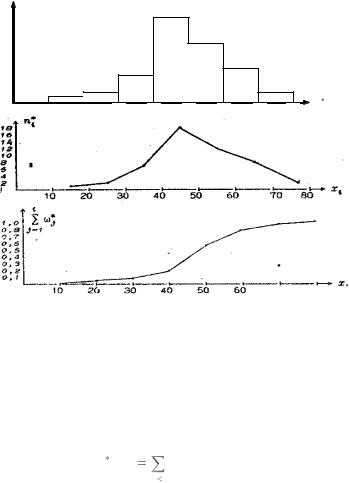
|
ni/10 |
|
|
|
|
|
|
|
|
|
1,8 |
|
|
|
|
|
|
|
|
|
1,6 |
|
|
|
|
|
|
|
|
Гисто- |
1,4 |
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
грамма |
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
xi |
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
|
Полигон
Кумулята
15.3. Эмпирическая функция распределения (ЭФР)
Эмпирической функцией распределения СВ X называется функция F*(x), определяющая для каждого значения х относительную частоту события (Х<х) F*(x)=nx/n, где nx - число выборочных значений, меньших х, a n - объем выборки.
По значениям накопленных относительных частот ЭФР определяется следующим образом:
F x |
ni / n . |
xi |
x |
В отличие от ЭФР, функция распределения генеральной совокупности F(x)=P(X<х) называется теоретической функцией распределения (ТФР).
Отметим, что разница между ТФР и ЭФР состоит в том, что ТФР определяет вероятность события (Х<х), а ЭФР определяет относительную частоту этого же события.
ЭФР обладает всеми свойствами ТФР, то есть: 1) значения F*(х) принадлежат отрезку [0,1];
130
