
Учебное пособие 2003
.pdf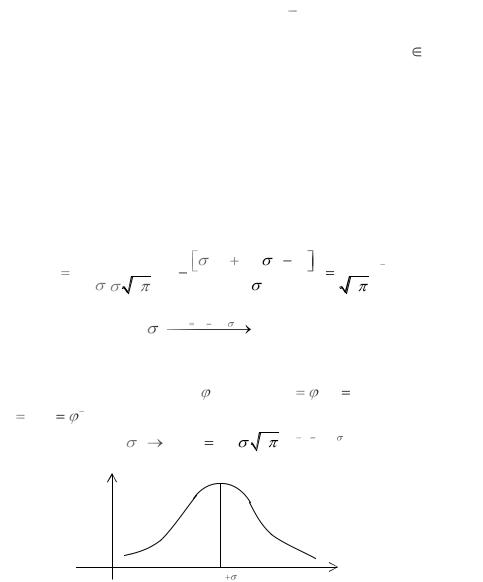
плотностями распределения [ |
1 |
f ( |
x b |
) ], где |
f(x) |
- |
|
|
|
||||||
|
|
a |
|
a |
|
|
|
фиксированная плотность раcпределения вероятностей, b |
R, |
||||||
а>0, является видом распределения. |
|
|
|
|
|
||
Используя |
введенные |
|
определения, |
можно |
|||
сформулировать утверждение. |
|
|
|
|
|
|
|
Линейное преобразование Y=aX+b СВ не меняет вида распределения.
Пример. Найти закон распределения СB. Y=(Х-т)/ζ, если СВ X подчиняется нормальному закону N(m,ζ).
В нашем случае Y=(1/ζ)Х-т/ζ, т.е. а=1/ζ, b=-т/ζ.
Вспоминая формулу для плотности распределения нормального закона N(m,ζ) и учитывая формулу (3), получаем
|
|
|
|
|
|
|
|
y |
m / |
m |
2 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
2 |
|
|||||||||
f |
y |
|
exp |
|
|
|
|
e y |
/ 2 , |
||||||||
m / |
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|||||
2 |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
т.е. |
СВ Y распределена по закону N(0,1). |
|
|
|
|
|
|
|
|
||||||||
|
Отсюда N m, |
|
Y X m / |
N 0,1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Логарифмически нормальное распределение. CB
X распределена нормально по закону N(m,ζ). Найти плотность
распределения |
СB. |
Y== |
(Х); |
|
y |
(x) ex отсюда |
|
x ln y |
1 ( y) |
и следовательно, |
|
|
|
||
|
|
|
|
|
|
||
|
N m, |
f x |
1/ |
2 e x m / 2 . |
|||
f(y)
0 |
em / 2 |
y |
Функция ех – монотонно возрастающая всюду. Используя формулу (3), находим
101

f y |
|
1 |
|
|
1 |
e ln y m / 2 . |
|
|
|
|
|
|
|||
|
|||||||
|
|
|
2 y |
||||
M y em / 2 , |
|
D y e2m e 1 . |
|||||
А.Н. Колмогоровым показано, что логарифмически нормальному закону подчиняются размеры частиц при дроблении.
Теорема. Пусть Х1 и Х2 – независимые СВ, а 1(х) и 2(х), х R – произвольные функции, тогда независимы и СВ.
Y1= 1(X1) и Y2= 2(X2).
Другими словами, функции от независимых СВ являются также независимыми СВ.
11.2. Системы функций нескольких СВ. Совместные законы распределения.
Снова для наглядности ограничимся случаем двух случайных величин. Пусть на вероятностном пространстве (Ω, ,Р) определены СВ Х1=Х1(ω) и Х2=Х2(ω), ω Ω, и пусть
F(x1,x2) – их совместная функция распределения. Рассмотрим некоторые функции от СВ X1 и Х2, т.е. новые СВ Y1 и Y2, связанные функциональными зависимостями с X1 и Х2:
Y1= |
1(X1,Х2)= |
1[X1(ω),Х2(ω)]=Y1(ω), |
|
Y2= |
2(X1,Х2)= |
2[X1(ω),Х2(ω)]=Y2(ω). |
|
Количество функций Yi может быть любым. Здесь |
|||
предполагается, |
что неслучайные функции 1 и 2 |
таковы, |
|
что Y1 и Y2 вновь являются СВ, определенными на том же |
|||
вероятностном пространстве (Ω, ,Р). Таким образом, |
Y1, Y2 |
||
являются сложными функциями ω, заданными на Ω. Основная задача, как и в случае функции одной СВ, состоит в том, чтобы, зная функцию совместного распределения F(x1,x2) и функции 1 и 2, найти функцию совместного распределения
СВ Y1 и Y2. Указанная задача решается легко. Действительно,
F(y1,y2)=P(Y1<y1, Y2<y2)=P( 1(X1,X2)<y1, 2(X1,X2)<y2) |
(4) |
102 |
|

Пусть теперь:
а) (Х1,Х2) - двумерная дискретная случайная величина и x1i, x2j - значения соответственно СВ X1 и X2, а рij=P(X1=x1i, Х2=x2j) - вероятности, с которыми принимаются эти значения
(i, j=1,2,…).
Тогда по формуле (4)
F y , y |
2 |
|
pij , |
1 |
i |
j |
|
|
|
i, j u
где суммирование проводится по всем индексам i, j, определяемым из условия
(i, j) u, u=((i,j)| 1(x1i,x2j)<y1, 2(x1i,x2j)<y2);
б) (Х1,Х2) – непрерывная двумерная случайная величина, f(x1,x2) – соответствующая плотность вероятности, тогда согласно (4) и формуле для вероятности попадания двумерной СВ в область, получим
F y1, y2 |
f x1, x2 dx1dx2 , |
|
D |
где область D определяется условием |
|
D=((x1,x2)| |
1(x1,x2)<y1, 2(x1,x2)<y2). |
При этом предполагается, что функции 1, 2 таковы,
что область D квадратируема.
Приведем формулы для функции распределения в том случае, когда имеется одна функция (Х,Y)=Z:
|
|
pij , |
если X,Y |
дискр. СВ, |
|
i j |
|
|
|
F z P Z z |
xi , x j |
z |
|
(5) |
|
|
|
||
|
|
f |
x, y dxdy, если |
X,Y непр. СВ, |
|
x, y |
z |
|
|
Зная ФР F(z), по известным правилам можно найти закон распределения в случае дискретной СВ. В случае непрерывной СВ плотность распределения вероятностей f(z) находится дифференцированием F(z) по переменной z если в точке z функция F(z) дифференцируема.
103

Пример. Найти функцию распределения и распределения СВ Z=XY, если двумерная СВ распределена по закону, определенному таблицей
xi |
yj |
-1 |
0 |
1 |
|
|
0 |
0,1 |
0,2 |
0,1 |
|
|
|
|
|
|
|
|
1 |
0,2 |
0,3 |
0,1 |
pij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
закон
(X,Y)
1.
Решение. По формуле (5) |
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
z |
1; |
|
|
F z |
pij или F z |
P Z |
z |
0,2 |
-1 |
z |
0; |
|||
0,9 |
0 |
z |
1; |
|||||||
i j |
|
|
|
|
||||||
|
xi y j |
z |
|
|
1 |
1 |
z. |
|
||
|
|
|
|
|
|
|
||||
Закон распределения СВ Z имеет вид |
|
|
|
|||||||
zi |
|
-1 |
|
0 |
|
1 |
|
|
|
|
pi |
|
0,2 |
|
0,7 |
|
0,1 |
pi |
1 |
|
|
Пример. (ФР произведения). Пусть (X,Y) – двумерная непрерывная СВ с плотностью вероятностей f(x,y). Найти ФР произведения Z=XY. По той же формуле (5) имеем
|
|
0 |
F z P XY z |
f x, y dxdy |
dx f x, y dy |
xy z |
|
z / x |
z / x
dx f x, y dy.
0
 y
y
z>0
z y= x
 x
x
z<0
Отсюда, дифференцируя по переменной z, получаем выражение для плотности распределения f(z)
104

0 |
1 |
|
1 |
f x, z / x dx . |
|
f z F z |
|
f x, z / x dx |
|
||
x |
x |
||||
|
0 |
|
Пример (ФР частного). Пусть (X,Y) – двумерная непрерывная СВ с плотностью вероятности f(x,y). Найти ФР и плотность распределения вероятностей частного Z=X/Y.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F z |
P X/Y |
|
z |
|
f |
x, y |
dxdy |
|
|
|
dy f |
x, y dx |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x / y |
z |
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|||||||
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
f |
x, y |
dx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f |
z |
|
F |
z |
yf |
yz, y |
|
dy |
|
yf |
|
yz, y |
dy . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||
1) z>0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)z<0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a)y>0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a)y>0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
|
|
|
|
|
|
|
|
|
x=zy |
|
|
|
|
y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) y<0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б)y<0; |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x=zy |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
11.3.Задача композиции
Водном из важных частных случаев функциональной зависимости Z= (Х,Y)=X+Y возникает задача определения
закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент.
Пусть (Х,Y) - двумерная непрерывная СВ с известной плотностью совместного распределения компонент f(x, у) и
Z=X+Y. Тогда
105

F z |
P Z z P X |
Y |
z |
f x, y dxdy |
|
|
|
x |
y z |
z |
x |
z |
y |
|
dx |
f x, y dy |
dy |
f x, y dx. |
|
y
x+y=z
0 |
x |
Cделав в интеграле замену переменной х=х; х+у=t и учтя, что якобиан отображения (x,y)→(x,t) равен 1, получим
|
z |
|
F z |
dt f x,t x dx. |
(6) |
Из формулы (6) следует, что СB Z имеет плотность вероятности
f z F z |
f |
x, z x dx . |
(7) |
Таким образом, если двумерное распределение |
|||
слагаемых X и Y имеет плотность |
f (x, y) , то и их сумма |
||
Z=X+Y также имеет плотность, определяемую равенством (2).
Если СВ X и Y независимы, то |
f (x, y) f (x) f ( y) и |
|
записывается в виде свертки функций f(х) и f(y): |
||
f z |
f x f z x dx |
f y f z y dy . |
Задача определения закона распределения суммы независимых случайных величин носит название задачи композиции.
Формула (6) дает решение этой задачи для случая двумерной непрерывной случайной величины. Аналогично рассматривается случай двумерной дискретной СВ.
106

Если (Х,Y) - двумерная дискретная СВ, то закон распределения Z=X+Y записывается в виде
P Z zk |
i |
P(X = xi , Y = y j ) , |
|
j |
|
|
xi |
y j zk |
где суммирование распространяется на все значения i и j, для которых выполняется условие xi+yj=zk.
В частности, если (X,Y) – двумерная дискретная СВ с независимыми компонентами, то
P Z zk |
P X xi P Y z xi . |
||
|
i |
|
|
12. РАСПРЕДЕЛЕНИЕ |
2 |
||
n |
|||
|
|
||
(Хи - КВАДРАТ С п СТЕПЕНЯМИ СВОБОДЫ) |
|||
12. 1. Определение |
2 -распределения. Плотность |
||
|
n |
|
|
распределения |
2 |
|
n |
||
|
n2 -распределение широко используется в разделе курса
теории вероятностей, называемом математической статистикой.
Пусть X1, Х2,…,Хn- независимые СВ, каждая из которых имеет стандартное нормальное распределение Хi N(0,1). n2 - распределением называется распределение CВ
|
|
|
2 |
X2 |
|
X2 ... |
X2 . |
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
Найдем |
плотность |
распределения |
2 . |
В дальнейшем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
будем писать вместо F 2 |
x |
и f 2 x |
просто F(х) и f(x). Для |
||||||||||||||
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
2 |
имеем ФР: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|||
|
F x P X2 |
x |
P |
|
x X |
x |
|
|
|
|
|
e t |
/ 2dt . |
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
1 |
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
Дифференцируя по переменной х, получаем плотность
107

распределения |
f x |
|
|
1 |
|
|
x1/ 2 e |
x / 2 , |
x 0 . |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
2 |
X2 |
X2 |
находим |
|
|
|||||||||||
|
|
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
1 |
|
|
|
|
|
|
|
1 |
|
|
x t 1/ 2 e 1/ 2 x t dt |
||
f |
|
x |
|
|
t 1/ 2e t / 2 |
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
1 |
x |
|
e x / 2 |
||
2 |
||
0 |
|
dt |
|
|
1 e |
x / 2 |
|
dt |
||
|
|
|
|
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
||
|
xt t2 |
|
0 |
|
x2 / 4 |
t x / 2 2 |
|||
1 |
e x / 2 arcsin |
t |
x / 2 |
2 |
|
x / 2 |
|
|
|
x |
e |
x / 2 |
|
|
|
||
|
|
|
|
|
|
|
. |
0 |
|
2 |
|
|
|
||
Продолжая такие вычисления дальше, можно получить
для |
2 |
формулу, |
справедливость которой устанавливается |
|
n |
||||
|
|
|
||
индукцией по п: fn |
x cn xn / 2 1 e x / 2 . |
|||
Для п = 1 формула справедлива. Допустив, что это соотношение выполняется для некоторого п, покажем, что оно справедливо и для п + 1:
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
cn |
|
x n |
1e t / 2 x t 1/ 2 e x t / 2dt |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f |
n |
1 |
x |
|
|
f |
n |
t f x t dt |
|
t 2 |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
cn |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
t |
|
xz; |
dt |
xdz |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
e x / 2 tn / 2 1 x t 1/ 2 dt |
t |
|
0; z 0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
t |
|
x; |
|
z |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
cn |
|
|
|
|
x |
xz n / 2 1 |
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
e x / 2 |
|
|
x xz |
xdz |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x / 2 cn |
|
x |
|
|
|
|
1/ 2 |
|
|
n 1 / 2 1 |
|
|
||||||
|
|
|
n / 2 1 |
|
1/ 2 |
|
|
|
|
n / 2 1 |
|
|
|
|
|
x / 2 |
|
||||||||||||
|
|
x |
|
|
|
|
x |
|
xe |
|
|
|
|
z |
|
1 |
|
z |
|
|
|
|
dz |
x |
|
e |
|
const. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, предположение индукции доказано. Постоянные сп найдем из условия нормировки
108

|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2z; |
dx |
2dz |
|
|
1 |
|
f |
n |
x dx c xn / 2 1e x / 2dx |
x 0; |
z 0 |
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
t |
x; |
z 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
c 2n / 2 1 zn / 2 1e z 2dz 2n / 2 c zn / 2 1e |
z dz 2n / 2 c |
n / 2 . |
|||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cn |
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2n / 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n / 2 |
|
|
|
|
|||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
fn x |
|
|
|
1 |
|
|
xn / 2 1e x / 2 , |
x 0 ; |
|
|
|||||
|
|
|
|
2 |
n / 2 |
n / 2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
n, |
D |
2 |
|
2n . |
|
|
|
||||||
|
|
|
|
|
|
n |
n |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь |
воспользовались известным |
соотношением |
|||||||||||||||||
1/ 2 |
|
|
|
, Г(1)=1, Г(п+1)=п!, Г(z+1)=zГ(z). |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
0
5 |
10 |
15 |
Раньше были даны определения числовых характеристик (в частности, математического ожидания и дисперсии) для одной случайной величины. Теперь рассмотрим вопрос о некоторых числовых характеристиках для функций СВ и случайных векторов.
12.2. Математическое ожидание функций случайных величин.
Теорема. Пусть Х – дискретная СВ, принимающая
109

значения х1, х2,… соответственно с вероятностями р1, р2,…, Y= (X) ( (X) – неслучайная функция) – новая СВ. Тогда
M(Y) M |
X |
xk pk , если |
ряд, |
стоящий |
справа, |
|
k |
1 |
|
|
|
абсолютно сходится.. |
|
|
|
|
|
Так |
как X - |
дискретная СВ, |
то |
Y= (X) |
- также |
дискретная СВ и ее значениями являются числа у1, у2,..., где множество (у1, у2,...) совпадает с множеством всех различных значений ( (х1), (х2),...), а вероятность каждого значения уj, равна
|
P Y y j |
P X y j |
|
pi . |
|
|
||
|
|
|
|
|
i: xi |
y j |
|
|
M Y |
y j P Y y j |
y j |
|
pi |
|
|
pi |
|
|
j 1 |
|
j 1 |
i: xi |
y j |
j 1 i: xi |
y j |
. |
|
|
|
|
|
|
|
|
|
|
xi pi |
|
xk |
pk |
|
|
|
|
j 1 i: xi |
y j |
k |
1 |
|
|
|
|
|
Так же можно получить формулу для вычисления |
||||||||
математического ожидания функции |
(Х, Y) двух дискретных |
|||||||
СВ X и Y: |
|
|
|
|
|
|
|
|
|
M X,Y |
|
|
xi , y j |
P X |
xi , Y |
|
y j . |
|
|
|
i 1 j 1 |
|
|
|
|
|
Аналогично может быть рассмотрен случай функций непрерывных СВ.
Теорема. Пусть Х – непрерывная СВ, имеющая плотность распределения вероятностей f(x), Y = (X). Тогда
M Y M |
X |
x f x dx , |
если интеграл абсолютно сходится. |
|
|
Для функции |
(Х,Y) двух |
непрерывных СВ с |
совместной плотностью распределения f(х,y) математическое ожидание имеет вид
110
