Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1439

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.16 Mб

Скачать

☆

1 / 131 2 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

А.И. БАРСУКОВ, М.Ю. ГЛАЗКОВА, В.И. МИНАКОВ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

ИАНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

ВЗАДАЧАХ И УПРАЖНЕНИЯХ ПОВЫШЕННОЙ СЛОЖНОСТИ

Учебное пособие

для студентов бакалавриата и специалитета 1-2 курсов

всех направлений подготовки

Воронеж 2017

УДК 517+514.12 (07) ББК 22.161+22.151.5я73

Б261

Рецензенты:

О.И. Канищева, к.ф.-м. н., доцент кафедры № 206 ВУНЦ ВВС «ВВА» им. проф. Жуковского Н.Е. и Гагарина Ю.А.;

кафедра математики и физики ФГБОУ ВО ВГАУ (зав. каф., докт. тех. наук, профессор В.П. Шацкий)

Барсуков, А.И.

Математический анализ и аналитическая геометрия в задачах и упражнениях повышенной сложности: учебное пособие для студентов Б261 бакалавриата и специалитета 1-2 курсов всех направлений подготовки / А.И. Барсуков, Глазкова М.Ю., В.И. Минаков; ВГТУ. – Воронеж,

2017. – 124 с.

ISBN 978-5-7731-0538-1

Пособие содержит теоретический материал по теории числовых и функциональных рядов, векторной алгебры и аналитической геометрии. Представлены решения задач повышенной сложности по этим темам.

Предназначено для подготовки студентов к олимпиадам по высшей математики, а также углубленного изучения высшей математики.

Ил.28. Библиогр.: 6 назв.

УДК 517+514.12 (07) ББК 22.161+22.151.5я73

Утверждено учебно-методическим советом ВГТУ в качестве учебного пособия

ISBN 978-5-7731-0538-1	©	Барсуков А.И., Глазкова М.Ю.,
		Минаков В.И., 2017
	©	ВГТУ, 2017
	2

ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ..................................................................................................................	4
1. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ .......................................................................	5
1.1. Первообразная и неопределенный интеграл...............................................	5
1.2. Определенный интеграл................................................................................	9
1.2.1.Определение. Условия интегрируемости..............................................	9
1.2.2. Вычисление определенных интегралов..............................................	15
1.2.2.1.Определенный интеграл и первообразная........................................	15
1.2.3. Теоремы о среднем и оценка интеграла .............................................	34
1.3. Несобственный интеграл.............................................................................	41
1.3.1. Вычисление несобственных интегралов.............................................	42
2. РЯДЫ......................................................................................................................	51
2.1. Числовые ряды .............................................................................................	51
2.1.1. Ряды. Сходимость ряда.........................................................................	51
2.1.2. Абсолютная и условная сходимость ряда. .........................................	59
2. 2. Функциональные ряды ...............................................................................	75
3. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.....................	91
3.1. Векторы в геометрических задачах............................................................	91
3.2. Аналитическая геометрия линейных .......................................................	102
геометрических объектов.................................................................................	102
3.2.1. Прямая на плоскости ..........................................................................	102
3.2.2. Плоскость и прямая в пространстве..................................................	107
3.3. Кривые второго порядка............................................................................	111
ЗАКЛЮЧЕНИЕ .......................................................................................................	124
БИБЛИОГРАФИЧЕСКИЙ СПИСОК....................................................................	124

ВВЕДЕНИЕ

В пособии рассмотрены два важных раздела курса математики: аналитическая геометрия и элементы математического анализа, включающие интегрирование функций одной переменной и теорию рядов. Основной целью издания является подготовка студентов к решению нестандартных задач, предлагаемых на различных олимпиадах для студентов технических и экономических специальностей и направлений подготовки.

Каждый раздел пособия снабжен кратким теоретическим материалом, характеризующим основные идеи и используемые методы. По большей части приводимые факты выходят за рамки стандартных курсов математики для нематематических специальностей. Основные приемы иллюстрируются примерами с решениями. Многие из представленных в пособии задач входили в те или иные студенческие олимпиады по математике, некоторые задачи составлены авторами пособия. При отборе задач и их решений авторы опирались на свой опыт по подготовке студентов к участию в региональных и всероссийских олимпиадах по математике. Кроме того, мы использовали свой опыт по организации и проведению подобных олимпиад.

1.ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

1.1.Первообразная и неопределенный интеграл

Определение 1. Функция F(x) называется первообразной (точной) для функции f (x) на промежутке X, если F'(x) = f (x) x X .

Имеют место следующие утверждения о существовании первообразной у функции f (x) , которые будут обоснованы далее в п.5.2.2.

Утверждение 1. Всякая непрерывная на промежутке X функция имеет

на X точную первообразную.

Соотношение F'(x) = f (x) определяет первообразную F(x) неоднознач-

но. Следующее утверждение устанавливает основное свойство первообразных.

Утверждение 2. Если F1 (x) и F2 ( x) – две первообразные функции f (x) на одном и том же промежутке, то их разность F1 (x) − F2 (x) постоянна на

этом промежутке.

Определение 2. Неопределенным интегралом для функции f (x) на про- межутке X называется множество всех ее первообразных на этом проме- жутке и обозначается ∫ f (x) dx .

Таким образом, если F(x) – какая-либо первообразная для функции f (x) на промежутке X , то

∫ f ( x) dx = F ( x) + c.

Нахождение неопределенного интеграла заключается в проведении преобразований подынтегрального выражения, позволяющих свести исходный интеграл к табличному или к сумме табличных интегралов. При этом использу-

ются следующие правила вычисления неопределенных интегралов:

1. ∫ a f ( x) dx = a∫ f ( x) dx,

a = const.

2. ∫ ( f1 (x) + f 2 ( x)) dx = ∫ f1 ( x) dx + ∫ f 2 ( x) dx.

3. Если

∫ f (x) dx = F ( x) + c

и ϕ(x)

- непрерывно

дифференцируемая

функция, то

∫ f (ϕ( x)) d (ϕ( x)) = F (ϕ(x))+ c .

(1.1)

Примеры решения задач

Пример 1.1. Найти интеграл ∫ e−

dx.

Решение. Функция

f (x) = e−

непрерывна на всей числовой оси R, по-

этому она имеет на R точную первообразную.

, x ≤

e x dx, x ≤ 0,

+ c, x ≤ 0,

e −

∫ e − x

∫

− x , x > 0.

dx =

e − x dx, x > 0.

− x + c , x > 0.

∫

− e

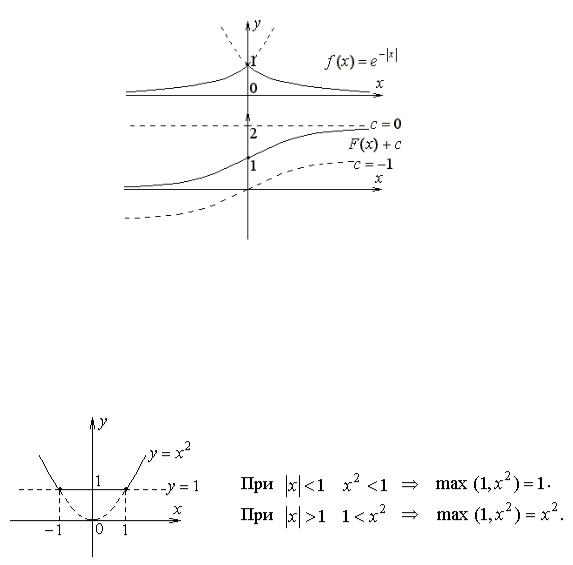
Так как по определению первообразная должна быть непрерывной функцией, то постоянные с и с1 не должны быть независимыми. Связь между ними получается из условия непрерывности в точке x = 0 :

lim (e x + c) = lim (−e		−x + c ),
x→−0	x→+0	1

которое дает равенство

1 + c = −1 + c1 c1 = 2 + c .

Окончательно получаем

		−	x	e x + c, x ≤ 0,
				e x + c, x ≤ 0,

∫	e			dx =	− e− x + c, x > 0.
	e			dx =
				2

Для наглядности можно сравнить графики подынтегральной функции и ее первообразных (рис. 1.1).

		Рис. 1.1.
Отметим, что первообразная F(x) дифференцируема при x=0.
Пример 1.2. Найти интеграл		∫ max (1, x 2 ) dx.
Решение. Для	наглядности	изобразим на одном графике функции
f1 (x) = 1 и f2 (x) = x2	(рис. 1.2).

Рис. 1.2.

+ c1,

x < −1,

1 dx,

< 1,

∫ max (1, x

∫

+ c,

< 1,

) dx =

> 1.

= x

∫ x2 dx,

+ c2 ,

x > 2.

Условие непрерывности первообразной в точке x = −1 дает

	x	3					1				2
lim			+ c	=	lim	(x + c) −		+ c	= −1 + c, c	= c −
	3
x→−1−0			1		x→−1+0	3		1	1	3

и в точке x = 1

		x3					1						2
lim (x + c) =	lim			+ c	2	1 + c =		+ c	2	c	2	= c +		.

x→1−0			3				3						3
	x→1+0

Итак, окончательно получаем

		x		3	−	2	+ c,	x < −1,


	2	3				3
∫ max (1, x	2			+ c,			−1 ≤ x ≤ 1,
∫ max (1, x		) dx = x		+ c,			−1 ≤ x ≤ 1,
				3		2
			x		+	2	+ c,	x > 1.
					+	3	+ c,	x > 1.
		3				3

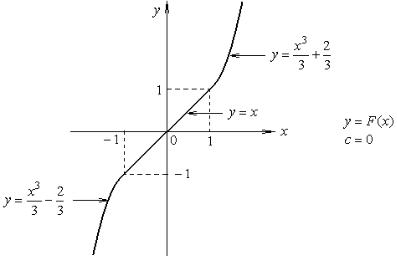
График первообразной при c = 0 (рис. 1.3):

Рис. 1.3.

Первообразная F(x) дифференцируема всюду на R , то есть является точ-

ной первообразной.

Рассмотрим далее нестандартные приемы нахождения неопределенных интегралов для некоторых функций.

Известно, что рациональные дроби всегда интегрируются в элементарных функциях путем разложения их на простейшие дроби. Но такой способ часто требует проведения большого объема вычислений. Иногда этого можно избежать, проводя некоторые преобразования и используя формулу (1.1.).

∫

Пример 1.3. Найти

dx .

Решение.

−1

∫

x 4 + 1

dx =

∫

x 4 − 2x 2 + 1 + 2x 2

dx = ∫

(x 2 − 1)2 + 2x 2

dx =

− 1

( x

− 1)(x

+ x

+ 1)

− 1)(x

+ x

−

(x 2 − 1) dx

x 2 dx

dx3

∫

+ 2∫

∫

+ x

+ 1

)

− 1

+ 1 +

− 1

x 2

d x +

= ∫

∫

d (x

3 )

x + x

−1

3 −1

+ c

3 +

−1

(x3 )2 −1

x +

x 2 − x + 1

x3 − 1

+ c .

x 2 + x + 1

x3 + 1

Аналогичный прием можно использовать и при нахождении неопределенных интегралов от некоторых иррациональных функций.

∫

Пример 1.4. Найти

−1

x4 +1

Решение.

x 2 + 1

d x

x 2

d x

∫

= ∫

x − 1

+ 1

−

− 2 + 2

x x 2

x 2

d x −

d t

= ∫

= =

x −

= t

= ∫

1 2

t 2 + 2

x −

+ 2

d t

= ∫

= −

∫

= −

+ 1 +

+ c =

t 2 1 +

1 +

t 2

x +

+ c .

= −

2 x

+ 1+

2 x2

+ c = −

x4 +1

2 −1)2

x2 −1

Задачи для самостоятельного решения

1. Пусть f : X → Y ратная.

Пусть ∫ f (x)

– непрерывная монотонная функция, а f −1 : Y → X – ее об- dx = F ( x) + c . Найти ∫ f −1 (x) dx.

Найти интегралы:

∫ x

x − 1

dx .

∫ min{5 − x 2 , 1, x 2 }dx .

Pn (x) dx

где

Pn (x) - многочлен степени n.

∫ (x − a)n+1

5. ∫

− x

∫

x 2 − 1

d x .

x8 + 1

(x 2 + x + 1)2

−1

7. ∫

d x .

∫

d x .

∫

d x

10.

∫

d x

1+ x

)

(2 + x

−1

d x

x 4 + 1

11.

∫

12.

∫

d x .

x4 +1

x 4 − 1

13. При каком соотношении между параметрами a, b, c, d интеграл

∫	a x	3 + b x		2 + c x + d
					dx
		x 2
			(x − 1) 2

представляет собой рациональную функцию?

1.2.Определенный интеграл

1.2.1.Определение. Условия интегрируемости

Определение 3. Если	функция f (x) определена	на [a, b] и
a = x0 < x1 < x2 <L< xn−1 < xn = b	(разбиение этого отрезка с	отмеченными
	9

точками

ξk [xk −1; xk ]=

k ,

k = 1, 2, K, n

то интегралом

(Римана) от

функции f (x) на [a, b] называется число

∫ f (x) d x =

max

lim

→0

∑ f (xk ) Dxk ,

Dxk = xk - xk −1 ,

k =1

если предел существует и не зависит от способа разбиения отрезка

[a, b] и от выбора точек

ξk

k .

Критерий интегрируемости функции. Для того, чтобы ограниченная

функция f (x) была интегрируема (по Риману) на отрезке [a, b],

необходимо и

достаточно, чтобы выполнялось равенство

max

lim

→0

∑wk ( f ; Dk ) Dxk = 0,

k =1

где

ωk ( f , k ) = sup

f (x') − f (x ')

колебание функции на частичном

x',x ' k

отрезке

k .

Из этого критерия следует, что а) непрерывная функция,

б) ограниченная монотонная функция, в) ограниченная функция, имеющая конечное число точек разрыва на

[a, b], интегрируемы (по Риману) на [a, b].

Примеры вычисления интегралов по определению

Пример 1.5. Вычислить интеграл ∫ (1 + x) d x

по определению.

Решение. Разобьем отрезок интегрирования [0, 1] на n

равных частей точ-

ками

, k = 0, 1, 2, K, n,

тогда

xk =

k . Выберем в качестве точек

ξ k

правые концы частичных промежутков,

то есть

, Kξ

= 1.

Нетрудно заметить,

что точки ξk

, k = 1, 2, K, n

образуют арифметическую

прогрессию.

f (x) = 1+ x

Интегральная сумма

S n для функции

имеет вид

Sn = ∑ 1

k =1

Преобразуем

S n следующим образом:

1 / 131 2 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.16 Mб2Учебное пособие 1434.pdf
#
30.04.20221.16 Mб16Учебное пособие 1435.pdf
#
30.04.20221.16 Mб4Учебное пособие 1436.pdf
#
30.04.20221.16 Mб111Учебное пособие 1437.pdf
#
30.04.20221.16 Mб2Учебное пособие 1438.pdf
#
30.04.20221.16 Mб15Учебное пособие 1439.pdf
#
30.04.2022300.67 Кб2Учебное пособие 144.pdf
#
30.04.20221.16 Mб3Учебное пособие 1440.pdf
#
30.04.20221.17 Mб4Учебное пособие 1441.pdf
#
30.04.20221.17 Mб1Учебное пособие 1442.pdf
#
30.04.20221.17 Mб6Учебное пособие 1443.pdf