
- •Рецензенты:
- •Некрасова, Н. Н.
- •ISBN 978-5-7731-0774-3
- •ОГЛАВЛЕНИЕ
- •4. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
- •4.1. Свойства и графики показательной и логарифмической функций
- •Показательную функцию также называют экспонентой по основанию a.
- •Сформулируем основные свойства показательной функции:
- •5º. Производная функции:
- •А также часто используемые на практике свойства степеней
- •Сформулируем основные свойства логарифмической функции:
- •7º. Производная функции:
- •4.2. Определение логарифма и его свойства
- •Из определения логарифма можно записать показательное уравнение
- •Пример. Записать с помощью знака логарифма:
- •б) согласно определению логарифма получаем уравнение
- •Свойства логарифмов
- •1º. Логарифм единицы равен нулю:
- •3º. Основное логарифмическое тождество:
- •5º. Формула для логарифма частного:
- •6º. Формула для логарифма степени:
- •8º. Формула перехода к новому основанию:
- •4.3. Тождественные преобразования показательных
- •Преобразование показательных и логарифмических выражений основаны на применении основных свойств соответствующих функций, показателя степени и свойств логарифмов.
- •Решение. Используя свойства степеней и основные логарифмические тождества, получим
- •Решение. Используя свойства логарифмов (3º, 9º), получим
- •Тогда получим
- •тогда
- •Решение. Логарифмируя обе части равенства, получим
- •Решение. Воспользовавшись свойствами логарифмов и потенцируя обе части равенства, получим
- •4.4. Показательные уравнения и неравенства
- •Решение показательных уравнений и неравенств основано на свойствах и монотонности показательной функции.
- •Пример. Решить уравнение
- •откуда
- •из которого находим
- •Ответ:
- •Полученное уравнение удобнее всего решать, введя новую переменную
- •Тогда уравнение сводится к квадратному относительно новой переменной
- •Ответ:
- •Введем новую переменную
- •придем к квадратному уравнению
- •откуда
- •Пример. Решить неравенство
- •Откуда
- •Ответ:
- •Решая последнее неравенство методом интервалов, получим
- •Ответ:
- •4.5. Логарифмические уравнения и неравенства
- •4.4. Вычислить:
- •4.5. Упростить выражение:

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Н. Н. Некрасова, В. В. Горяйнов, А. С. Чесноков, С. С. Сумера
МАТЕМАТИКА: УРАВНЕНИЯ И НЕРАВЕНСТВА
Учебное пособие
Воронеж 2019
УДК 512.13(075.8)
ББК 22.141я7 М34
Рецензенты:
кафедра математического моделирования Воронежского государственного университета
(зав. кафедрой д-р физ.-мат. наук, профессор В. А. Костин); канд. физ.-мат. наук, доц. кафедры высшей математики Воронежского
государственного педагогического университета И. Ю. Покорная
Некрасова, Н. Н.
Математика: уравнения и неравенства: учебное пособие /
М34 Н. Н. Некрасова, В. В. Горяйнов, А. С. Чесноков, С. С. Сумера; ФГБОУ ВО «Воронежский государственный технический
университет». – Воронеж: Изд-во ВГТУ, 2019. – 101 с.
ISBN 978-5-7731-0774-3
Учебное пособие содержит подробное изложение материала по некоторым разделам элементарной математики. Теоретический материал сопровождается подробными решениями примеров и задач. По каждой теме представлено большое количество задач для самостоятельного решения.
Предназначено для вводного адаптационного этапа преподавания математики на русском языке для иностранных граждан института международного образования и сотрудничества.
Ил. 42. Табл. 1. Библиогр.: 13 назв.
УДК 512.13(075.8)
ББК 22.141я7
Печатается по решению учебно-методического совета Воронежского государственного технического университета
ISBN 978-5-7731-0774-3 |
© Некрасова Н. Н., Горяйнов В. В., |
|
Чесноков А. С., Сумера С. С., 2019 |
|
© ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2019 |
2
ОГЛАВЛЕНИЕ |
|
Введение……………………….……………………………………….. |
4 |
1. АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА ………………………… |
5 |
1.1. Основные понятия и определения.............................................. |
5 |
1.2. Линейные неравенства …………...……………………………. |
6 |
1.3. Неравенства второй степени…………………………………... |
7 |
1.4.Рациональные неравенства…………………………………….. 12
1.5.Неравенства, содержащие знак модуля……………………….. 17
1.6.Иррациональные неравенства…………………………………. 23
1.7. Задания для самостоятельной работы………………………… 26
2.СИСТЕМЫ УРАВНЕНИЙ ……………………………………….. 28
2.1.Линейные системы двух уравнений с двумя
неизвестными…………………………………………………… |
29 |
2.2. Методы решения линейных систем уравнений…………...…. |
30 |
2.2.1.Метод подстановки…………………………………….. 30
2.2.2.Метод алгебраического сложения
(линейного преобразования) ………………………….. 31
2.2.3. Графический способ решения линейных систем…….. |
33 |
2.3. Методы решения нелинейных систем уравнений…………..... |
36 |
2.3.1. Метод подстановки……………………………………... |
36 |
2.3.2. Метод алгебраического сложения уравнений………… |
36 |
2.3.3.Метод разложения на множители……………………... 38
2.3.4.Метод замены переменных…………………………….. 39
2.4. Задания для самостоятельной работы ………………...……… |
43 |
3. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ……..…….. |
45 |
3.1. Задания для самостоятельной работы…………………….…... |
55 |
4.ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ... 57
4.1.Свойства и графики показательной и логарифмической
функций………………………………………………………… 57
4.2.Определение логарифма и его свойства………………………. 62
4.3.Тождественные преобразования показательных и
логарифмических выражений…………………………………. 64
4.4. Показательные уравнения и неравенства………………........... 66
4.5.Логарифмические уравнения и неравенства………………….. 72
4.6.Системы показательных и логарифмических уравнений……. 78
4.7. Задания для самостоятельной работы ………………...……… |
81 |
5. ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ……………………………… |
86 |
Ответы к заданиям для самостоятельной работы………………... |
90 |
Заключение……………………………………………………………. |
101 |
Библиографический список…………………..…………………….. |
101 |
3
ВВЕДЕНИЕ
Учебное пособие по математике предназначено для иностранных граждан, готовящихся к поступлению в высшие учебные заведения России. Пособие содержит краткое изложение курса математики по следующим темам:
алгебраические неравенства, системы уравнений и неравенств, показательные и логарифмические уравнения (неравенства). Настоящее пособие является продолжением учебного пособия Н.Н. Некрасовой, В.В. Горяйнова и В.А. Поповой «Математика: вводный курс» (издательство ВГТУ, 2017).
При составлении пособия авторы стремились учесть неоднородность математической и языковой подготовки, полученной иностранными гражданами на родине. В основу структуры пособия положен принцип компактности, доступности и наглядности изучаемого материала.
Изложение материала ориентировано на овладение иностранными учащимися необходимой элементарной математической терминологией, а также успешного усвоения последующих разделов курса математики на русском языке.
В данном учебном пособии при раскрытии содержания вводимых понятий и терминов широко используется международный символический язык математики: обозначения, рисунки, таблицы и т.д. Посредством знакомой учащимся математической символики создается смысловая опора, облегчающая понимание и усвоение материала.
Работа с пособием рассчитана на второй семестр. Однако авторы предусмотрели возможность его использования уже в конце начального этапа обучения. Пособие содержит теоретический материал и примеры с ответами, как для аудиторных занятий, так и для самостоятельной работы.
Предлагаемое учебное пособие поможет иностранным учащимся в подготовке к сдаче экзамена по математике первого сертификационного уровня.
Все приведенные в пособии иллюстрации выполнены авторами.
Авторы выражают благодарность кандидату физ.-мат. наук, доценту А.Б. Кущеву, внимательно прочитавшему рукопись. Его ценные замечания и рекомендации помогли улучшить содержание пособия.
4
1.АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА
1.1.Основные понятия и определения
Выражение вида
R(x) > Q(x) или R(x) < Q(x) , |
(1.1) |
где R(x) и Q(x) – многочлены относительно неизвестной x , называется
алгебраическим неравенством с одним неизвестным.
Поскольку областью определения многочленов R(x) и Q(x) состоит из множества действительных чисел, то задачу о решении неравенства (1.1)
можно сформулировать так: найти все числовые значения буквы x , каждое из которых обращает (1.1) в верное числовое неравенство. Каждое такое числовое
значения называется решением неравенства (1.1) . Решить неравенство (1.1)
значит найти множество всех его решений. В случае, если множество всех решений неравенства (1.1) есть пустое множество, то говорят, что (1.1) не
имеет решений.
Два алгебраических неравенства R(x) >Q(x) и T (x) < S(x) называются
равносильными, если любое решение первого неравенства является решением второго, и, наоборот, любое решение второго неравенства является решением первого. В силу этого определения любые два неравенства, не имеющие решений, равносильны. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Равносильный переход принято обозначать двойной стрелкой . Запись
R(x) >Q(x) T (x) < S(x)
обозначает, что неравенства R(x) >Q(x) и T (x) < S(x) равносильны.
Приведем некоторые утверждения, при помощи которых совершаются равносильные переходы:
1. Неравенства R(x) > Q(x) и R(x) −Q(x) > 0 равносильны.
2. Неравенства R(x) >Q(x) и R(x) + a >Q(x) + a равносильны для любого
действительного числа а .
3. Для любого числа а > 0 неравенства R(x) >Q(x) и aR(x) > aQ(x) ‒ равносильны, для числа а < 0 неравенства R(x) >Q(x) и aR(x) < aQ(x) будут
равносильными.
4. Пусть известно, что для любого действительного числа x справедливо неравенство R(x) =T (x) , тогда равносильны неравенства R(x) >Q(x) и
T (x) >Q(x) .
5
1.2. Линейные неравенства
Линейным неравенством называется неравенство вида
|
a1x +b1 > a2 x +b2 или a1x +b1 < a2 x +b2 , или a1x +b1 ≥ a2 x +b2 , |
|
||||||||||||
|
|
или a1x +b1 ≤ a2 x +b2 , |
|
(a1 ≠ a2 ) |
|
|
|
|
(1.2) |
|||||
где a1, a2 , b1, b2 – некоторые числа, причем a1 ≠ 0, a2 ≠ 0 . |
|
|
|
|
|
|
||||||||
Если |
a1 = a2 = a |
и b1 = b2 |
= b , то |
неравенства |
|
(1.2) |
примут |
более |
||||||
простой вид |
ax > b (ax < b, |
ax ≥ b, |
|
ax ≤ b). |
|
|
|
|
|
′ |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
(1.2 ) |
|||||||
В зависимости от знака a решение (1.2 ) будет иметь вид: |
|
|
||||||||||||
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
1) если a > 0, то решение имеет вид x |
> |
b |
|
|
b |
;+∞ |
|
|
||||||
a |
|
или x |
|
; |
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|||
2) если a < 0, то решение будет вида |
x |
< |
b |
или |
x |
|
|
b |
|
|||||
a |
−∞; |
. |
|
|||||||||||
Если |
a =0 , то неравенство |
|
|
|
|
|
|
|
|
a |
|
|||
(1.2 ) примет вид |
0 x >b. |
Причем, если |
||||||||||||
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
b ≥ 0 оно не имеет решения, а если |
b < 0 оно верно при x R. |
|
|
|||||||||||
Пример. Решить неравенство 15 −6x ≥ 0. |
|
|
|
|
|
|
|
|
||||||
Решение. ОДЗ: |
x R. Перенесём |
в правую |
часть |
число |
15 с |
|||||||||
противоположным знаком, получим |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−6x ≥ −15 . |
|
|
|
|
|
|
|
|
|
||
Затем, разделим обе части неравенства на (–6), при этом |
знак |
|||||||||||||
неравенства изменится на противоположный: |
|
|
|
|
|
|
|
|
|
|||||
|
|
x ≤ 15 , |
x ≤ |
5 или |
x ≤ 2,5 . |
|
|
|
|
|
|
|||
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Ответ: x (−∞; 2,5].
Пример. Решить неравенство 2x +3 >1−4x .
Решение. ОДЗ: x R. Перенесем в левую часть неравенства неизвестные, а в правую часть − числа, изменив их знаки на противоположные:
2x + 4x >1−3 или 6x > −2.
Разделим обе части полученного неравенства на 6, при этом знак неравенства не изменится:
6

x > −62 или x > −13 .
Ответ: x −1;+∞ .3
Пример. Решить неравенство 3 + x + |
2 − x < 0 . |
|
|
|
4 |
3 |
|
Решение. ОДЗ: x R. Умножаем обе части неравенства на 12: |
|
||
3(3 + x) + 4(2 − x) < 0 |
или |
9 +3x +8 −4x < 0 . |
|
После преобразований получим |
|
|
|
−x +17 < 0 |
или |
−x < −17 , |
|
откуда |
|
|
|
x >17. |
|
|
|
Ответ: x (17;+∞) . |
|
|
|
1.3. Неравенства второй степени |
|
||
Рассмотрим квадратное неравенство |
|
|
|
ax2 +bx +c > 0 , (a ≠ 0) |
(1.3) |
||
Для решения неравенства (1.3) применим метод интервалов, |
который |
||
состоит в следующем: |
|
|
|
1) на числовую ось наносят корни уравнения ax2 +bx + c = 0 , |
причем |
||
отмечают их на числовой оси либо закрашенным, когда неравенство нестрогое, (т.е. корни удовлетворяют данному неравенству), либо светлыми кружками, когда неравенство строгое (корни не удовлетворяют ему);
2) определяют знак |
соответствующего выражения для значения x в |
|||
каждом полученном интервале. |
|
|
||
Изменение |
знаков |
удобно |
иллюстрировать с |
помощью параболы |
y = ax2 +bx +c. |
Для неравенства (1.3) схематическое расположение параболы |
|||
относительно оси Ox при a > 0 изображено на рис. 1.1. |
Решение неравенства |
|||
имеет вид (−∞; x1) (x2 ;+∞), где x1 |
и x2 ‒ корни квадратичной функции. |
|||
+ +
x1 x2 х
Рис. 1.1. Геометрическая иллюстрация решения неравенства (1.3) при a > 0
7
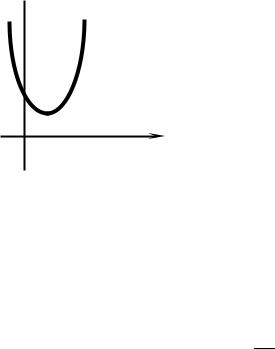
Применяя тождественное преобразование «выделение полного квадрата», получим
|
2 |
|
b 2 |
D |
|
, |
||
ax |
|
+bx + c = a x + |
|
|
− |
|
|
|
|
|
4a2 |
||||||
|
|
|
2a |
|
|
|
||
|
|
|
|
|
|
|
|
|
где D =b2 − 4ac . Поэтому неравенство (1.3) |
равносильно неравенству |
|
||||||||||||
|
|
b 2 |
|
D |
|
|
> 0, (a ≠ 0). |
(1.4) |
||||||
a x + |
|
|
|
− |
|
|
|
|
|
|
||||
|
|
4a |
2 |
|
||||||||||
|
|
2a |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим два случая когда a > 0 и когда a < 0. |
|
|||||||||||||
1. Пусть a > 0. Тогда неравенство (1.4) равносильно неравенству |
|
|||||||||||||
|
|
b 2 |
|
|
D |
|
|
> 0, (a > 0) . |
|
|||||
x + |
|
|
|
− |
|
|
|
|
|
(1.5) |
||||
|
|
4a |
2 |
|
|
|||||||||
|
2a |
|
|
|
|
|
|
|
|
|||||
Если D < 0 , то при любом числовом значении неизвестного x = x0 в левой
части неравенства (1.5) |
|
|
|
b 2 |
||
стоит сумма неотрицательного |
x0 |
+ |
|
|
и |
|
|
||||||
|
|
|
|
2a |
|
|
положительного числа |
|
− |
D |
|
, т.е. неравенство |
(1.5) |
превращается в верное |
|
|
|
|
|
|||||
4a |
2 |
|||||||
|
|
|
|
|
|
|
|
|
числовое неравенство (см. рис. 1.2).
y 
0 |
х |
Рис. 1.2. График квадратичной функции (a > 0, D < 0)
Следовательно, неравенство (1.5) справедливо при любом x . Другими словами, множество всех решений неравенства (1.5) в этом случае есть
множество всех действительных чисел.
Если D = 0 , то очевидно, что неравенство (1.5) превращается в верное числовое неравенство для любого числа x , кроме x0 = −2ba . Следовательно,
8

множество всех решений неравенства (1.5) в этом случае есть множество
|
|
b |
|
|
b |
|
|
|
|
−∞;− |
|
|
|
− |
|
;+∞ . |
|
|
2a |
|
||||||
|
|
2a |
|
|
|
|
||
Если D > 0 , то неравенство (1.5) равносильно неравенству |
|
|||||||
(x − x1)(x − x2 ) > 0, (a > 0) , |
(1.6) |
|||||||
где x = |
−b − |
D |
|
, |
|
|
|
||
1 |
2a |
|
|
|
|
|
|
||
метод интервалов,
(−∞; x1) (x2 ;+∞).
x = |
−b + |
D |
|
. Очевидно, |
что |
x < x , поэтому, |
применяя |
||
|
|
|
|||||||
2 |
2a |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
множество |
всех |
решений |
(1.6) |
в виде |
||
2. Пусть a < 0. Тогда неравенство (1.4) равносильно неравенству
|
b 2 |
D |
< 0 , (a < 0) . |
|
|||
x + |
|
|
− |
|
|
(1.7) |
|
|
4a |
2 |
|||||
|
2a |
|
|
|
|
||
Если D < 0 , то очевидно, что для любого числа x это неравенство превращается в неверное числовое неравенство, т.е. неравенство (1.7) не имеет
решений (см. рис. 1.3).
y
0 |
х |
Рис. 1.3. График квадратичной функции (a <0, D <0)
Если D = 0 , то очевидно, что неравенство (1.7) не имеет решений. Если D > 0 , то (1.7) равносильно неравенству
|
|
|
|
|
|
|
(x − x1)(x − x2 ) < 0 , (a < 0) , |
|
(1.8) |
|||
|
−b − |
|
|
|
|
|
−b + |
|
|
. Очевидно, что x > x , |
|
|
где x = |
D |
|
, x |
|
= |
D |
поэтому, применяя |
|||||
1 |
2a |
|
|
|
2 |
|
2a |
1 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
метод интервалов, получим, что множество всех решений неравенства (1.8) есть интервал (x1; x2 ) .
9

Аналогично проводится решение неравенства ax2 +bx + c < 0 (a ≠ 0).
Приведенные выше рассуждения можно отобразить в таблице.
Отметим, что запоминать эту таблицу не надо, для решения конкретного квадратного неравенства лучше каждый раз решать соответствующее квадратное уравнение, затем применить либо метод интервалов, либо графический метод для данного квадратичного трехчлена.
В таблице подразумевается, что корни x = −b − |
D |
и x = −b + |
D |
||
1 |
2a |
2 |
2a |
||
|
|
||||
расположены в порядке возрастания: x1 < x2 .
Решение неравенств второй степени
|
a |
D |
Неравенство |
|
|
Решение неравенства |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
D > 0 |
ax2 +bx + c > 0 |
|
|
(−∞; x1 ) (x2 ;+∞) |
|
|
|||||||
|
|
ax2 +bx + c < 0 |
|
|
|
(x1; x2 ) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
−∞;− |
b |
|
|
b |
|
;+∞ |
|
|
|
|
|
ax2 +bx + c > 0 |
|
|
|
|
− |
|
|
|
|
|||
|
|
|
|
2a |
2a |
|
|||||||||
|
a > 0 |
D = 0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ax2 +bx + c < 0 |
|
|
нет решений |
|
|
|
|
|||||
|
|
D < 0 |
ax2 +bx + c > 0 |
|
|
|
(−∞;+∞) |
|
|
|
|
||||
|
|
ax2 +bx + c < 0 |
|
|
нет решений |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
D > 0 |
ax2 +bx + c > 0 |
|
|
|
(x1; x2 ) |
|
|
|
|
|
|||
|
|
ax2 +bx + c < 0 |
|
|
(−∞; x1 ) (x2 ;+∞) |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
ax2 +bx + c > 0 |
|
|
нет решений |
|
|
|
|
|||||
|
a < 0 |
D = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞;− |
b |
|
|
b |
|
;+∞ |
|
|
||
|
|
|
ax2 +bx + c < 0 |
|
|
|
|
− |
|
|
|
|
|||
|
|
|
|
2a |
2a |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
D < 0 |
ax2 +bx + c > 0 |
|
|
нет решений |
|
|
|
|
|||||
|
|
ax2 +bx + c < 0 |
|
|
|
(−∞;+∞) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример. Решить неравенство x2 − x −6 < 0 . |
|
|
|
|
|
|
|
|
||||||
|
Решение. |
ОДЗ: |
x R. Применим метод интервалов. |
Поскольку корни |
|||||||||||
квадратного трехчлена |
f (x) = x2 − x −6 |
есть x =3 и x |
= −2 , то |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
10

f (x) = (x −3)(x + 2) .
Значит исходное неравенство равносильно неравенству
(x −3)(x + 2) < 0 .
Определим знак последнего неравенства в каждом интервале (рис. 1.4),
+ |
|
+ |
-2 |
3 |
х |
Рис. 1.4. Иллюстрация знаков, соответствующих данному неравенству
получим, что множество всех решений исходного неравенства есть интервал
(−2;3) .
Ответ: x (−2;3).
Пример. Решить неравенство −x2 − 2x +3 > 0 .
Решение. ОДЗ: x R. Применим графический метод. Решив уравнение
−x2 − 2x +3 = 0,
получим
x1 = −3, x2 =1.
Графиком функции
y = −x2 − 2x +3
является парабола, ветви которой направлены вдоль отрицательных значений оси OY (т.е. вниз). При x (−3;1) график функции лежит выше оси абсцисс
(см. рис. 1.5).
y
−3 |
0 |
1 |
х |
|
|
|
|
Рис. 1.5. График функции y = −x2 − 2x +3
11

Следовательно, решением исходного неравенства будет множество значений x , заключённое в интервале между корнями уравнения.
Ответ: x (−3;1).
1.4. Рациональные неравенства
Рациональной функцией называется отношение двух многочленов
f (x) = Pn (x) ,
Qm (x)
где Pn (x) и Qm (x) − многочлены соответственно степеней n или m, т.е.
P |
(x) = a |
n |
xn +... + a x + a |
, |
Q |
(x) = b xm +... +b x +b . |
|||
n |
|
1 |
0 |
|
m |
m |
1 |
0 |
|
Соответственно рациональными неравенствами называются неравенства, содержащее рациональные функции. Такими будут неравенства вида:
Pn (x) > 0 или Pn (x) < 0, |
(при |
Qm (x) ≡1) |
||
|
Pn (x) |
> 0 или |
Pn (x) |
< 0, |
|
|
|||
|
Q (x) |
|||
|
Q (x) |
|||
|
|
|
||
|
m |
|
m |
|
Неравенства часто решаются методом интервалов. Этот метод основан на одном важном свойстве рациональной функции: в интервале между двумя соседними нулями рациональная функция сохраняет знак. Если рассматривается дробно-рациональная функция, то те значения переменной x, при котором функция обращается в нуль, будем называть нулями функции (точки числителя), а точки, при которых знаменатель дроби обращается в нуль − точками разрыва функции.
На числовой оси отмечают все нули и точки разрыва функции f (x) (если
они есть). При этом числовая ось разбивается на конечное число интервалов, на каждом из которых левая часть неравенства сохраняет постоянный знак. Чтобы установить этот знак, достаточно взять любую точку из интересующего нас промежутка и определить знак функции в этой точке. Что касается самих точек, то в случае строгого неравенства точки обозначают светлыми кружками. Это означает, что сами точки не входят во множество решений данного неравенства. В случае нестрогого неравенства точки нулей функции наносят на числовую прямую закрашенными кружками, а это означает, что сами точки также входят во множество решений данного неравенства. Понятно, что во всех случаях точки разрыва функции обозначают светлыми кружками.
Следует отметить, что наибольшие трудности в методе интервалов возникают при определении знаков на соответствующих промежутках.
Сформулируем правило расстановки знаков, которое поможет нам
12
определять знаки в каждом из промежутков. Рассмотрим рациональное неравенство вида:
(x −α )k1 |
(x −α |
2 |
)k2 |
... (x −α |
n−1 |
)kn−1 |
(x −α |
n |
)kn > 0, |
(1.9) |
1 |
|
|
|
|
|
|
|
где k1, k2 ,..., kn−1, kn − фиксированные натуральные числа, α1, α2 ,...,αn−1, αn − фиксированные действительные числа, среди которых нет равных, и такие, что
α1 <α2 <... <αn−1 <αn .
Неравенство (1.9) решается обобщённым методом интервалов. Рассмотрим многочлен
P(x) = (x −α )k1 |
(x −α |
2 |
)k2 |
...(x −α |
n−1 |
)kn−1 |
(z −α |
n |
)kn . |
(1.10) |
1 |
|
|
|
|
|
|
|
|||
Очевидно, что для любого числа x0 , такого, что x0 > an , |
соответствующее |
|||||||||
числовое значение любого сомножителя в произведении (1.10) положительно, поэтому числовое значение P(x0 ) многочлена P(x) также положительно.
Для любого числа x1 , взятого из интервала (an−1,an ), соответствующее
числовое значение любого сомножителя, кроме последнего, положительно; соответствующее числовое значение последнего сомножителя положительно, если kn − четное число, и отрицательно, если kn − нечетное число. Поэтому
число P(x1) − положительно, если kn − четное число, и P(x1) − отрицательно, если kn − нечетное число. Обычно в этих случаях говорят, что многочлен P(x) при переходе через точку an меняет знак, если kn − нечетное число, и не меняет знака, если kn − четное число.
Аналогично показывается, что если известен знак многочлена P(x) на интервале (ai ;ai+1) , то на интервале (ai−1,ai ) знак определяется по правилу: многочлен P(x) при переходе через точку ai меняет знак, если ki − нечетное число, и не меняет знака, если ki − четное число. На этом рассуждении и
основан обобщенный метод интервалов.
На числовую ось наносятся числа α1, α2 ,..., αn−1, αn . Над лучом справа от наибольшего из этих чисел, т.е. справа от an , ставят знак плюс, над следующим за ним справа налево интервалом ставят знак плюс, если kn − четное число, и знак минус, если kn − нечетное число. Н ад следующим за ним справа налево интервалом ставят знак, пользуясь правилом: многочлен P(x) при переходе через точку an−1 меняет знак, если kn−1 − нечетное число, затем рассматривается
следующий за ним справа налево интервал. В нем ставят знак, пользуясь тем же правилом, таким образом, рассматриваются все промежутки.
Решением неравенства (1.9) будет объединение всех промежутков, в которых поставлен знак плюс.
13
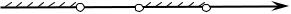
Пример. |
Решить неравенство (x +1)(x + 6)(x − 4) < 0. |
Решение. |
ОДЗ: x R. Рассмотрим функцию f (x) = (x +1)(x + 6)(x − 4). |
Найдем нули функции, для чего решим уравнение
f (x) = 0
или
(x +1)(x + 6)(x − 4) = 0 ,
откуда
x1 = −1, x2 = −6, x3 = 4.
Отметим эти точки на числовой прямой. Так как мы решаем строгое неравенство, то все точки отмечаем светлыми кружками. На полученных промежутках каждый из множителей (x +1), (x +6) и (x − 4) сохраняет знак, и,
следовательно, сохраняет знак все выражение.
Для определения знаков в промежутках достаточно знать какой знак имеет функция в одном из промежутков, и, используя свойство чередования знаков, определим их во всех остальных промежутках. При этом удобно начинать с крайнего справа промежутка (4;+∞) , так как в нём значение
функции заведомо положительно. Объясняется это тем, что при значениях |
x , |
|
взятых правее |
наибольшего из нулей функции, каждый |
из |
множителей(x +1), |
(x +6) и (x −4) положителен. |
|
Определим теперь, используя свойство определения знаков на числовой прямой, знаки данной функции в каждом из остальных промежутков (рис . 1.6).
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
−6 |
|
−1 |
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 1.6. Геометрическая |
иллюстрация решения неравенства |
|
|||||||||||||
|
|
|
(x +1)(x + 6)(x − 4) < 0 |
|
|
|
|
|
|||||||
Как видно |
из рис. |
1.6, те |
значения x , при |
которых |
f (x) < 0 |
||||||||||
(заштрихованы), |
лежат в |
промежутках(−∞;−6),(−1;4) . |
Решение |
данного |
|||||||||||
неравенства представляет собой объединение указанных промежутков.
Ответ: x (−∞;−6) (−1;4).
Пример. Решить неравенство x3 ≥ 9x .
Решение. ОДЗ: x R. Запишем неравенство в виде x3 −9x ≥ 0 .
Разложим кубический многочлен на множители и вынесем общий множитель за скобки:
14
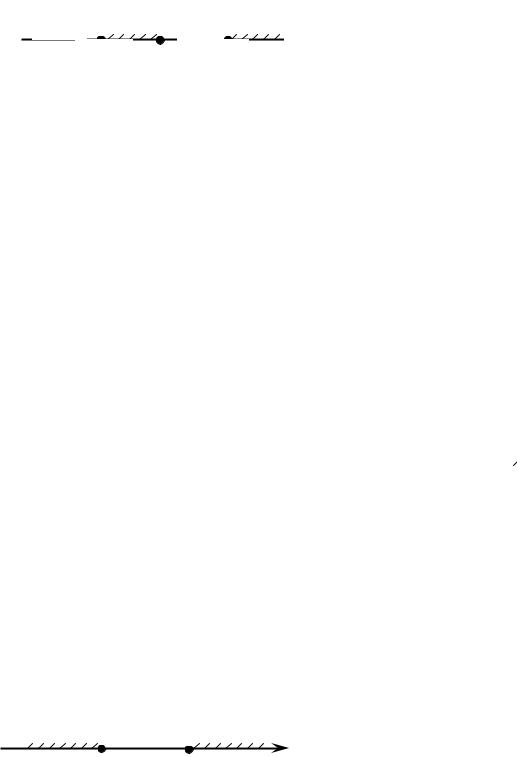
x(x2 −9) ≥ 0 или |
x(x −3)(x +3) ≥ 0. |
|
Функция обращается в нуль |
при |
x1 = 0, x2 = 3, x3 = −3. Решая |
неравенство методом интервалов, получим решение, соответствующее кривой знаков на рис. 1.17.
+ +
−3 |
0 |
3 |
x |
|
Рис. 1.7. Геометрическая иллюстрация решения неравенства x3 ≥ 9x
Ответ: x [−3;0] [3;+∞) .
Пример. Решить неравенство 2x2 −52x − 2 ≤1. 3x − x −7
Решение. ОДЗ: 3x − x2 −7 ≠ 0. Перенесём единицу из правой части в левую и упростим полученное выражение:
|
|
2x2 −5x − 2 |
−1≤ 0 |
|
|
|
|
|
|||||||||||
|
|
3x |
− x2 −7 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
3x2 −8x +5 |
|
|
|
|
|
|||||
2x2 −5x − 2 −3x + x2 + 7 |
≤ 0 |
, |
|
|
|
≤ 0 |
|
|
|
||||||||||
3x − x2 −7 |
|
|
|
|
|
−(x2 −3x +7) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3x2 −8x +5 |
≥ 0. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x2 −3x + 7 |
|
|
|
|
|
|
|
|
|
|||||||
Заметим, что x2 −3x +7 > 0 |
|
при любом |
|
x R, так |
как |
дискриминант |
|||||||||||||
D < 0 (a =1 > 0). Тогда имеем равносильное неравенство |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
3x2 −8x +5 ≥ 0 . |
|
|
|
|
|
|||||||||
Решая уравнение 3x2 −8x +5 = 0, найдем |
|
его корни x |
|
= 5 |
, x |
2 |
=1, затем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
методом интервалов определим решение неравенства (см. рис. 1.18). |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
− |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
5/3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.8. Геометрическая иллюстрация решения неравенства 3x2 −8x +5 ≥ 0
15

Ответ: x (−∞;1] |
|
2 |
|
|
|
1 |
3 |
;+∞ . |
|
|
|
|
|
|
|
|
|
Пример. Решить неравенство |
(6x −5)(2 + x2 ) |
≤ 0. |
|||
|
|
|
|
(4 − x2 )x |
|
Решение. ОДЗ: (4 − x2 )x ≠ 0. Запишем неравенство в виде
(6x −5)(2 + x2 ) ≤ 0. −(x2 −4)x
Умножим обе части полученного неравенства на (-1), при этом знак неравенства изменится на противоположный
(6x −x25)(2 +xx2 ) ≥ 0. ( − 4)
Заметим, что |
множитель 2 + x2 > 0 |
|
при |
всех |
|
x R . |
В |
этом |
случае |
||
полученное неравенство равносильно неравенству |
|
|
|
|
|
|
|||||
|
|
6x −5 |
|
≥ 0. |
|
|
|
|
|
|
|
|
|
(x − 2)(x + 2)x |
|
|
|
|
|
|
|
||
Откуда нули |
функции получаются |
при |
x = |
5 |
, |
а при |
x |
= ±2 |
x = 0 |
||
|
|
|
|
|
1 |
6 |
|
|
2,3 |
4 |
|
функция не существует. Выпишем решение неравенства, используя метод интервалов, геометрическая иллюстрация которого приведена на рис. 1.19.
+ |
|
|
+ |
|
+ |
− |
2 |
0 |
5/6 |
2 |
x |
|
|||||
|
|
|
|
|
Рис. 1.9. Геометрическая иллюстрация решения исходного неравенства
|
|
0; |
5 |
|
|
|
|
|
|
|
|
Ответ: x (−∞;−2) |
6 |
(2;+∞). |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Пример. Решить неравенство |
(x −2)3 (x +1)4 (x +3)5 (x −6) |
|
≤ 0. |
|
|||||||
|
|
||||||||||
|
|
|
|
|
|
x2 (x −4) |
|
|
|
|
|
Решение. |
ОДЗ: x2 (x −4) ≠ 0. |
Нули функции: x = 2, |
x |
2 |
= −1, |
x = −3, |
|||||
x4 = 6. Точки разрыва функции: |
|
|
1 |
|
|
|
3 |
||||
x5 = 0, x6 = 4. |
|
|
|
|
|||||||
На кривой |
знаков (рис.1.10) |
нули функции отметим |
закрашенными |
||||||||
16

кружками, а точки разрыва – светлыми. Будем определять знак функции в каждом интервале, пользуясь обобщенным методом интервалов. При переходе через x2 = −1 и функция знак не меняет, так как множители, откуда
найдены эти корни стоят в чётной степени.
+ |
− |
− |
+ |
|
|
+ |
− |
− |
0 |
2 |
4 |
6 |
x |
3 |
1 |
|
|
|
||
Рис. 1.10. Геометрическая иллюстрация решения данного неравенства |
||||||
Ответ: x [−3;0) U(0;2] U(4;6].
1.5. Неравенства, содержащие знак модуля
Неравенства вида
| f (x) |≤ g(x)
равносильно двойному неравенству
|
f (x) ≤ g(x), |
(1.11) |
−g(x) ≤ f (x) ≤ g(x) или системе |
|
f (x) ≥ −g(x).
Заметим, что в системе должны выполняться оба неравенства, что соответствует союзу «и».
Неравенства вида
| f (x) |≥ g(x)
равносильно объединению неравенств
|
f (x) ≥ g(x), |
(1.12) |
|
|
|
f (x) ≤ −g(x). |
|
|
Объединение неравенств означает, что должно выполняться хотя бы одно из неравенств, что соответствует союзу «или».
Пример. Решить неравенство x − 2 < 3.
Решение. ОДЗ: x R. Решим это неравенство тремя способами.
17

Способ 1
Известно что a 2 = a2 . Учитывая, что обе части данного неравенства
неотрицательны при всех x , то возведение в квадрат обеих частей не меняет знака неравенства, поэтому получим равносильное неравенство вида
(x −2)2 <32 ,
или
x2 − 4x −5 < 0.
Найдем корни x1 = −1 и x2 = 5, а затем определим решение неравенства методом интервалов, которое проиллюстрировано на рис. 1.11.
+ +
−1 5 х
Рис. 1.11. Графическая иллюстрация решения неравенства
Следовательно, −1< х <5 .
Ответ: х (−1; 5).
Способ 2
По определению модуля |
|
|
|
|
|
|
x −2 |
|
x −2, |
если |
x −2 ≥ 0 |
|
|
= |
|
|
|
|
|
|
2 − x, |
если |
x −2 < 0 |
|
|
|
|||
Следовательно, данное неравенство равносильно совокупности двух систем:
x −2 ≥ 0,x −2 < 3;x −2 < 0,2 − x < 3.
Решая первую систему, получим
x ≥ 2,x <5;
откуда 2 ≤ x <5.
18

Решая вторую систему, получим
x < 2,x > −1;
т.е. −1< x ≤ 2.
Объединяя найденные решения двух систем, находим решение исходного неравенства: −1< х <5 (рис. 1.12).
−1 |
2 |
5 |
х |
|
Рис. 1.12. Графическая иллюстрация решения данного примера
Ответ: −1< х <5 .
Способ 3
Заметим, что геометрически x − 2 можно рассматривать как расстояние на числовой прямой между точками x и 2 (см. рис. 1.13).
|
3 |
3 |
|
−1 |
2 |
5 |
х |
|
Рис. 1.13. Геометрическое представление x −2 < 3
Следовательно, нужно найти все такие точки x , которые находятся от точки с координатой 2 меньше, чем на 3 единицы. Из рис. 1.13 очевидно, что искомое решение есть интервал (−1; 5).
Ответ: −1< х <5 .
Замечание. Из приведённых способов решения в общем случае наиболее предпочтительным является первый (хотя второй способ является наиболее универсальным, но с технической точки зрения он относительно сложен) в данном примере для линейной функции проще всего геометрический способ.
Пример. Решить неравенство 4x −3 ≤ 2x +3 .
Решение. ОДЗ: x R. Так как обе части неравенства неотрицательны, возведем обеих частей неравенства в квадрат. Получим
(4x −3)2 ≤ (2x +3)2 ,
или после преобразований
12x2 −36x ≤ 0,
19

|
|
|
|
x2 −3x ≤ 0, |
|
|
|
x(x −3)≤ 0. |
|
|
|
|||||||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
0 ≤ x ≤3 , |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
так как ветви параболы направлены вверх, то она расположена ниже оси ОX |
||||||||||||||||||||||||||||
между корнями |
x1 = 0 и x2 |
= 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: x [0; 3]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Решить неравенство |
|
2x −5 |
|
|
≥1. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. ОДЗ: x ≠ −1. |
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Данное неравенство равносильно неравенству |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2x −5 |
2 |
≥1, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2x −5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1≥ 0. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разлагая левую часть на множители, имеем |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2x −5 |
|
|
|
|
|
|
2x −5 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
+ |
1 |
≥ 0 |
, |
|
|
||||||
|
|
x +1 |
|
|
|
|
x +1 |
|
|
|||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
|
|
|||||
|
|
x −6 |
|
3x − 4 |
|
|
|
|
|
|
|
|
3 x − |
3 |
(x − |
|
|
|||||||||||
|
|
|
≥ 0, |
|
|
|
|
|
|
|
|
|
|
≥ 0, |
|
|||||||||||||
|
|
|
|
x +1 |
|
|
|
|
|
|
(x +1)2 |
|
|
|
||||||||||||||
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Функция обращается в нуль при |
|
|
|
|
|
|
x = |
4 , |
x |
2 |
= 6 и |
не существует в |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
точке x3 = −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расставим |
их в порядке возрастания |
и согласно знаку |
||||||||||||||||||||||||||
неравенства на числовой оси (см. рис. 1.14). |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||
|
|
|
−1 |
|
|
|
|
|
4 3 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
х |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Рис. 1.14. Графическая иллюстрация решения |
|
||||||||||||||||||||||||||
Ответ: x (−∞;−1) |
−1; 4 |
[6;∞). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Решить неравенство |
|
x2 − 4x +3 |
|
≤3x − x2 . |
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
20

Решение. ОДЗ: x R. Перейдём к равносильной системе по формуле
(1.11):
x2 |
−4x +3 ≤ 3x − x2 , |
|
2 |
−4x +3 −3x + x |
2 |
≤ 0, |
|||
|
|
|
|
x |
|
|
|||
|
−4x +3 ≥ −(3x − x2 ); |
|
2 −4x +3 +3x − x2 ≥ 0; |
||||||
x2 |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−7x +3 ≤ 0, |
|
|
2 |
−7x +3 ≤ 0, |
|
|
|
2x |
|
2x |
|
|
|
|||
|
−x +3 ≥ 0; |
x ≤ 3. |
|
|
|||||
Отдельно найдем решение первого неравенства методом интервалов:
|
|
|
= 1 |
2x2 −7x +3 ≤ 0 . |
Точки x = 3, |
x |
2 |
‒ нули функции. Решение неравенства показано на |
|
1 |
|
2 |
|
|
|
|
|
|
рис. 1.15.
+ +
1 |
3 |
х |
|
||
2 |
|
|
Рис. 1.15. Графическая иллюстрация решения неравенства 2x2 −7x +3 ≤ 0
Следовательно, |
|
1 |
|
x |
2 |
;3 . |
|
|
|
|
Тогда система неравенств примет вид
1 ≤ x ≤ 3,2
x ≤ 3.
Изобразим на рис. 1.16 пересечение решений.
1 |
3 |
2 |
|
Рис. 1.16. Решение системы неравенств
х
1 ≤ x ≤ 3,2
x ≤ 3.
21
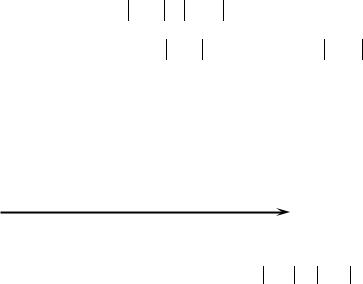
Таким образом, решение системы |
1 |
≤ x ≤3. |
||
|
1 |
|
2 |
|
|
|
|||
Ответ: x |
2 |
;3 . |
|
|
|
|
|
|
|
Пример. Решить неравенство x +1 − x − 2 < 3.
Решение. ОДЗ: x R. При x = −1, x +1 = 0; при x =2, x − 2 = 0. Точки −1 и 2 разбивают числовую прямую на три промежутка. Определим знаки
подмодульных выражений на образовавшихся промежутках. При |
x < −1 оба |
|||||
модуля раскрываются со знаком «−». |
|
|
При −1 ≤ x ≤ 2 |
первый модуль |
||
раскрывается со знаком «+», а второй со знаком «−». При |
х > 2 |
оба модуля |
||||
раскрываются со знаком «+» (см. рис. 1.17). |
|
|
|
|
|
|
|
+ − |
|
|
+ + |
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
−1 |
2 |
|
|
|||
|
|
|
||||
Рис. 1.17. Знаки подмодульных выражений x +1 и x −2
Решим данное неравенство на каждом из промежутков:
1.Пусть x < −1, тогда имеем
−x −1+ x −2 <3
или
−3 <3,
значит, x R и данное неравенство выполняется при х < −1;
2. |
Пусть −1 ≤ x < 2, тогда |
|
откуда |
х +1+ х −2 <3, |
2 x <4, |
х < 2. |
|
|
|
|
|
Значит, −1≤ x < 2; |
|
|
3. |
Пусть х ≥ 2 , тогда |
|
|
х +1− х + 2 <3, |
3<3. |
Это неверно, значит, при х ≥ 2 данное неравенство не имеет решений. |
||
Объединяя полученные решения, получим |
x < 2 . |
|
Ответ: x (−∞; 2).
22
1.6. Иррациональные неравенства
Иррациональным неравенством называется неравенство, содержащее неизвестную величину под знаком корня (радикала).
При решении иррациональных неравенств используются те же приемы, что и при решении иррациональных уравнений. Если при решении иррациональных уравнений можно проверить найденные корни, то при решении иррациональных неравенств проверка подстановкой, как правило, невозможна, так как обычно решением неравенства является бесконечное множество.
Вместе с тем всякое иррациональное неравенство, содержащее переменное под знаком квадратного корня, после преобразований приводится к
одному из видов: |
|
|
|
(1.13) |
||||
|
|
|
|
< g(x) |
|
|
||
|
|
f (x) |
|
|
||||
или |
|
|
|
(1.14) |
||||
|
f (x) |
> g(x). |
|
|
||||
Неравенство вида (1.13) равносильно системе неравенств |
||||||||
|
|
|
|
|
||||
f (x) ≥ 0, |
|
|
|
(1.15) |
||||
g(x) > 0, |
|
|
|
|||||
|
2 |
. |
|
|
||||
f (x) < (g(x)) |
|
|
||||||
Аналогично нестрогое неравенство |
|
≤ g(x) |
равносильно системе |
|||||
f (x) |
||||||||
неравенств |
|
|
|
|
||||
f (x) ≥ 0,g(x) ≥ 0,
f (x) ≤ (g(x))2.
Неравенство вида |
(1.14) |
равносильно |
совокупности |
||||
неравенств: |
|
|
|
|
|
|
|
|
|
f (x) ≥ 0, |
|
f (x) ≥ 0, |
|
|
|
|
а) |
б) |
g(x) ≥ 0, |
|
|
||
|
|
|
|
|
|||
|
|
g(x) < 0; |
|
|
2 |
. |
|
|
|
|
|
|
f (x) > (g(x)) |
|
|
двух систем
(1.16)
Пример. Решить неравенство 
 3x −1 < x + 4 .
3x −1 < x + 4 .
Решение. Данное неравенство имеет вид (1.13), следовательно, оно равносильно системе неравенств (1.15)
23

или
x ≥ 13
3x −1 ≥ 0, |
|
|
|||||
|
|
|
|
|
|
|
|
x +4 > 0, |
|
|
|||||
|
|
|
|
|
|
2 |
; |
3x −1< (x +4) |
|
||||||
|
|
|
1 |
|
|
|
|
x |
≥ |
3 |
, |
|
|
||
|
|
|
|
|
|
|
|
x > −4, |
|
|
|||||
|
2 |
+ |
5x +17 > |
0. |
|||
x |
|
||||||
|
|
|
|
|
|
|
|
Откуда |
|
|
1 |
|
|
|
|
|
≥ |
, |
|
|
|||
x |
3 |
|
|
||||
|
|
|
|
|
|
||
|
2 |
+ |
5x +17 > |
0. |
|||
x |
|
||||||
Но x2 +5x +17 > 0 верно при любом x R , так как D < 0 и a =1 > 0. Тогда есть решение данного неравенства.
Ответ: x 1 ; +∞ .3
Пример. Решить неравенство 
 x2 − x −6 > x .
x2 − x −6 > x .
Решение. Данное неравенство имеет вид (1.14), значит, оно равносильно совокупности систем неравенств (1.16):
|
2 |
− x −6 ≥ 0, |
x |
2 |
− x −6 |
≥ 0, |
|
|
б) x ≥ 0, |
|
|
|
|||||
а) x |
|
|
|
|
||||
x < 0; |
|
2 |
− x −6 |
> x |
2 |
. |
||
|
|
|
x |
|
|
|||
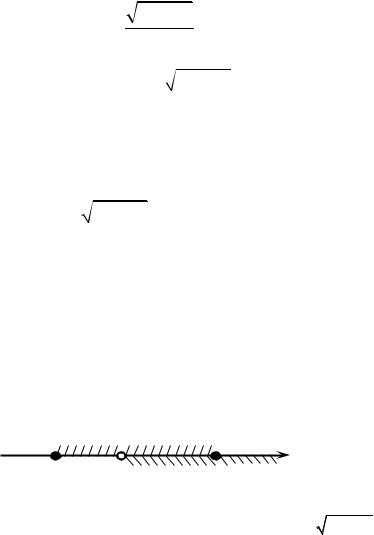
Решая систему а), для квадратного неравенства имеем x1 = 3, x2 = −2 ‒ нули функции. Пересечение решений системы а) изображено на рис. 1.18.
+ |
|
|
+ |
−2 |
0 |
3 |
х |
|
Рис. 1.18. Графическое изображение решение системы а)
Следовательно, x ≤ −2 .
При решении системы б) надо учесть, что первое неравенство является
24
следствием третьего неравенства, тогда система б) равносильна системе
x ≥ 0,
x2 − x −6 > x2 ;
или
x ≥ 0,x < −6;
которая не имеет решений.
Следовательно, решение системы а) будет и решением исходного неравенства.
Ответ: x (−∞; −2].
Пример. Решить неравенство 
 3x2 + 4 ≥ 4. x −1
3x2 + 4 ≥ 4. x −1
Решение. ОДЗ: x ≠ −1. Так как 
 3x2 + 4 > 0 при любом x R , то из
3x2 + 4 > 0 при любом x R , то из
данного неравенства имеем
х −1 > 0, т.е. х >1.
Умножив обе части неравенства на х −1 > 0, запишем данное неравенство в виде

 3x2 + 4 ≥ 4(x −1).
3x2 + 4 ≥ 4(x −1).
Так как обе части неравенства положительны, то, возведя в квадрат, получим равносильное неравенство
|
|
3x2 + 4 ≥16x2 −32x +16 , |
|
|
|
|
|
|
|
|
|||
|
|
|
13x2 −32x +12 ≤ 0. |
|
|
|
|
|
|
6 |
|
||
Решая полученное неравенство методом интервалов, имеем |
≤ x ≤ 2. |
||||||||||||
13 |
|||||||||||||
Учитывая, что х >1, решение неравенства показано на рис. 1.19. |
|
||||||||||||
|
|
|
|||||||||||
6 |
1 |
2 |
х |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
13 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.19. Графическое изображение решения неравенства |
|
3x2 |
+ 4 |
|
≥ 4 |
|
|||||||
|
x −1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Ответ: x (1; 2].
25

1.7.Задания для самостоятельной работы
1.1.Решить линейные неравенства:
1. 2x −3 ≤ 0. |
|
|
|
2. 5x −6 > 4 −6x. |
|
3. 2(x −3) > 4 +5x. |
|||||||||||||||||||||||||
4. 5(x −2) < 6x −13. |
|
|
5. |
|
x −3 |
<1. |
|
|
|
6. |
|
4 −3x |
≥ −1. |
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
||||
7. 5x + 9 > (8x + 3) −(3x −1). |
8. 5x −8 + 3 −2x |
> 0. |
9. |
|
x +1 |
−2x +2 1 |
≥ 0. |
||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|||||
10. |
|
x |
−3 |
1 |
>1 3 |
|
− 5 x. |
|
|
11. |
|
|
x +1 |
− 2x +5 |
≤ 0. |
12. |
2x −1 |
≤ 3 − x . |
|
||||||||||||
|
5 |
|
|
3 |
4 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|
8 |
|
6 |
|
|||
13. |
|
x −1 |
|
x +3 |
|
x |
14. |
|
|
x |
|
|
|
x |
|
4. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
+ |
|
|
>1− |
|
. |
|
|
− |
|
< |
|
15. |
3x −1 ≤8 +2x. |
|||||||||||||||
4 |
|
2 |
|
6 |
2 |
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
17. |
|
|
x |
|
|
|
x |
|
x |
|
18. |
2x +1 |
|
|
||||||
16. |
3 −2x < x −9. |
|
|
|
|
− |
|
|
− |
|
≤ 5. |
|
|
≥1. |
|
||||||||||||||||
|
|
4 |
|
2 |
6 |
7 |
|
|
|||||||||||||||||||||||
19. |
2 −5x ≥14 − x. |
20. |
2 − x |
+1< |
2x −1 |
− |
2x −3 |
. |
|
|
||
4 |
10 |
6 |
|
|
||||||||
|
1.2. Решить неравенства: |
|
|
|
|
|
|
|
|
|
||
1. 3(x −5)2 ≤ 0. |
2. |
x2 ≥ −1. |
|
|
|
3. |
x2 < 9. |
|||||
4. x2 ≥ 25. |
5. |
3x2 <8. |
|
|
|
|
6. |
(x −1)2 <16. |
||||
7. (2x +1)2 ≥ 25. |
8. |
(2x −1)2 > −3 |
|
|
9. |
3x2 + x −2 ≥ 0. |
||||||
10. |
x2 + x +12 > 0. |
11. |
−x2 − x +20 ≥ 0. |
|
|
12. |
(3x −4)2 ≥13. |
|||||
13. |
2x2 +7x +3 ≤ 0. |
14. |
x2 − x + 6 < 0. |
|
|
15. |
−x2 +2x +8 ≤ 0. |
|||||
16. |
x2 + x > 0. |
17. |
x2 −5x +4 ≤ 0. |
|
|
18. |
x2 +2x −6 ≤ 2. |
|||||
19. |
(6x −7)2 ≤ 3. |
20. |
2x2 −3x −2 > 0. |
|
|
|
|
|
||||
1.3.Решить неравенства,
1.xx −+23 < 0.
3. (x −1)(x + 3)(x − 4) < 0.
5. x +2 9 < x −x 6 .
используя обобщенный метод интервалов:
2.2x −−8x ≤1.
4.x(x −2) < 0.
x+4
6.x12+x2 − 7xx −−153 < 0.
26
7. |
|
x −8 |
> |
2 |
|
. |
8. x3 |
−6x2 +11x −6 < 0. |
|||||
x2 −5x +4 |
x +1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
9. |
|
x −5 |
< x. |
|
|
|
|
10. |
|
1−6x |
|
< 2. |
|
|
|
|
|
|
|
2x2 −3x |
−2 |
||||||
|
|
x +5 |
|
|
|
|
|
|
|||||
11. |
|
x3 −3x2 + x +1 ≥ 0. |
|
12. |
|
x2 (x +1)3 > 0. |
|
|
|
|
|
|||||
13. |
(x +4)5 (x −1)4 (x −2)7 < 0. |
14. |
(x +5)7 (x −1)4 (x +3)2 (7 − x)3 ≤ 0. |
|||||||||||||
15. |
|
x(x +2)5 |
|
≤ 0. |
|
16. |
|
x2 (x +3)5 |
|
|
≥ 0. |
|
|
|
||
|
(x −1)3 (x −3)6 |
|
|
(x −1)(x −2)4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
17. |
|
x4 −2x2 −8 |
< 0. |
|
18. |
|
x2 − x −2 |
|
|
|
≤ |
0. |
|
|||
|
(x2 +2x +1)3 |
|
|
(x +1)(x2 − x |
+1) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(x +1)(x2 +1) |
|
|
|
(x −1)(x + |
|
|
|
|
|
|||||
19. |
|
≥ 0. |
20. |
|
3)(x − |
2) ≥ 0. |
||||||||||
|
(x −3)(2 − x)(−4 − x2 ) |
|
(2x +1)(5x −7) |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1.4. Решить неравенства содержащие знак модуля: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
|
|
|
−3x |
|
|
≤ 0. |
|
2. |
|
|
|
|
x −3 |
|
≥ 5. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
x2 −9x |
|
> 0. |
|
|
5. |
|
|
|
|
2x −1 |
|
< |
|
3x +1 |
|
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
7. |
|
|
|
x +3 |
|
≥ |
|
x |
|
. |
|
|
|
|
8. |
|
|
|
|
x −1 |
|
+ |
|
|
|
x +1 |
|
< 4. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
10. |
|
x2 + x −6 |
|
≥ −x2 − x +6. |
|
11. |
|
2x +5 |
|
<1. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13. |
|
x2 −3x |
|
|
|
|
|
|
|
|
14. |
|
4x +1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
< 2. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2x −1 |
|
− |
|
x −4 |
|
> 4. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1.5. Решить иррациональные неравенства: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
≤ 0. |
2. |
|
|
|
|
≥ 0. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 −2x |
|
x +3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
≤ −2. |
5. |
|
|
|
< 3 − x. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2x −4 |
|
x −1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
7. |
|
|
|
|
x2 −4 ≥ x. |
8. |
|
x2 −3x −10 <8 − x. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
10. |
|
|
|
x2 +2x −8 > x −1. |
11. |
|
|
−x2 −3x +4 > x +1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
13. |
|
|
|
≤ x −5. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
11− x |
14. |
|
|
2x2 −3x −5 < x −1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3x −5 > −3.
6.3x −5 > 9x +1.
9. |
|
2x2 −12x +13 |
|
≥ 3. |
|||||||||||
|
|
||||||||||||||
12. |
|
|
|
x |
|
− |
|
x +2 |
|
> 1. |
|||||
|
|
|
|
|
|||||||||||
15. |
|
|
|
|
|
|
|
|
|
3 |
|||||
|
|
|
|
||||||||||||
|
|
|
x2 + x −6 |
|
< x. |
||||||||||
|
|
|
|
||||||||||||
3. |
|
|
2 + x |
≥ 4. |
||||||
6. |
|
|
|
|
|
≤ x −1. |
||||
|
x +5 |
|||||||||
9. |
|
|
|
|
|
|
|
|||
|
|
3x − x2 < 4 − x. |
||||||||
12. |
|
|
|
|
|
|
> 2 − x. |
|||
|
|
|
5x − x2 |
|
||||||
|
|
|
< x +4. |
|||||||
15. 2 4 − x2 |
|
|||||||||
27
2. СИСТЕМЫ УРАВНЕНИЙ
Пусть заданы два уравнения
F1(x, y) = 0 и F2 (x, y) = 0 .
Будем считать, что первое из уравнений задает на плоскости XOY линию Г1 , а второе – линию Г2 . Чтобы найти точки пересечения этих линий, надо
найти все пары чисел (x0 ; y0 ) такие, что при подстановке x0 и y0 в каждое
уравнение, получаются верные числовые равенства. Если поставлена задача об отыскании всех таких пар чисел, то говорят, что задана система уравнений, и записывают эту систему с помощью фигурной скобки в следующем виде:
F (x, y) = 0, |
(2.1) |
1 |
|
F2 (x, y) = 0. |
|
Решить систему (2.1) – это значит найти все пары чисел (x; y) , такие, что
при подстановке их в каждое уравнение системы (2.1), они обращаются в истинные равенства или доказать, что таких пар чисел не существует.
Аналогично определяется понятие системы уравнений с тремя и большим числом неизвестных.
Определение. Две системы уравнений
F (x, y) = 0, |
и |
F (x, y) = 0, |
1 |
3 |
|
F2 (x, y) = 0; |
|
F4 (x, y) = 0; |
называют равносильными (эквивалентными), если любая пара чисел (x0 ; y0 ) ,
удовлетворяющая первой системе, удовлетворяет и второй, а любая пара чисел, удовлетворяющая второй системе, удовлетворяет первой. То есть системы уравнений равносильны, если множество их решений совпадает.
Решение системы не изменится, если:
1) изменить порядок уравнений в системе (т.е. поменять уравнения местами);
2)если обе части какого-либо уравнения умножить (разделить) на ненулевой множитель;
3)если одно из уравнений заменить его суммой с другим уравнением, при этом оба уравнения могут быть умножены на нулевые множители.
Преобразования 1‒3 называют элементарными. Равносильные
(эквивалентные) системы получаются одна из другой с помощью
элементарных преобразований.
28

2.1. Линейные системы двух уравнений с двумя неизвестными
Система линейных уравнений с двумя переменными имеет вид
a x +b y = c , |
(2.2) |
||
1 |
1 |
1 |
|
a2 x +b2 y = c2 , |
|
||
где a1, a2 , b1, b2 , c1, c2 − некоторые числа, x и y − переменные.
Для решения системы (2.2) можно воспользоваться одним из следующих методов:
1)метод подстановки;
2)метод алгебраического сложения;
3)графический способ.
Число решений системы уравнений (2.2) можно определить по коэффициентам при соответствующих переменных x и y :
1. Если коэффициенты при неизвестных x и y не пропорциональны, т.е.
a1 ≠ b1 , то система имеет единственное решение. Графически это означает, что a2 b2
прямые, соответствующие графикам уравнений, пересекаются в точке (x0 ; y0 )
(рис.2.1).
 y a1x + b1y = c1
y a1x + b1y = c1
y0
a2 x + b2 y = c2
x0 0 |
х |
Рис. 2.1. Графическая иллюстрация единственного решения системы
2. Если a1 = b1 ≠ c1 , то система не имеет решений. В этом случае прямые, a2 b2 c2
являющиеся графиками уравнений системы, параллельны (рис. 2.2).
3. Если a1 = b1 = c1 , то система имеет бесконечное множество решений. a2 b2 c2
Графически это означает, что соответствующие уравнениям графики (прямые) совпадают (рис. 2.3).
29
 y
y
0 |
х |
Рис. 2.2. Графическая иллюстрация, когда система не имеет решения
 y
y
0 |
х |
Рис 2.3. Графическое изображение множества решений системы
В последних трех соотношениях записаны не дроби, а пропорции – они имеют смысл и в том случае, когда некоторые из знаменателей равны нулю.
2.2. Методы решения линейных систем уравнений
Основными методами решения таких систем являются метод подстановки и метод линейного преобразования (называемые также методом исключения и методом алгебраического сложения уравнений соответственно). Эти методы основаны на утверждениях о равносильности (эквивалентности) систем уравнений (преобразования 1‒3, стр. 28).
2.2.1. Метод подстановки
Методом подстановки удобно решать такие системы линейных уравнений с двумя неизвестными, у которых хотя бы один из коэффициентов при неизвестном x или y равен ±1.
2x + y =9,
Пример. Решить систему уравнений
3x −2y =10.
30
Решение. Выразим y через x из первого уравнения системы: |
y =9 − 2x . |
||||
Полученное выражение подставим |
вместо |
y во второе уравнение данной |
|||
системы: |
|
3x − 2(9 − 2x) =10 . |
|
||
|
|
|
|||
Получили уравнение, содержащее одну переменную x . Откуда находим x : |
|||||
|
|
3x −18 + 4x =10 , |
|
||
|
|
7x =10 +18, 7x = 28 x = 4. |
|
||
А затем, |
учитывая подстановку, определим соответствующее значение y : |
||||
|
|
y = 9 −2 4 y =9 −8 =1. |
|
||
Итак, пара (4;1) является решением данной системы. |
|
||||
Ответ: x = 4, |
y =1. |
|
|
|
|
|
|
|
x + y =1, |
|
|
Пример. Решить систему уравнений |
|
|
|||
|
|
|
4x −3y =11. |
|
|
Решение. Из первого уравнения системы выразим неизвестное |
x через y |
||||
(можно и наоборот, |
так как коэффициенты |
при неизвестных x и |
y равны |
||
единице) |
|
|
|
|
|
|
|
x =1− y , |
|
|
|
тогда второе уравнение системы будет иметь вид |
|
||||
|
|
4(1− y) −3y =11 или 4 − 4y −3y =11, |
|
||
|
|
−7 y =11− 4 , |
−7 y = 7 y = −1, |
|
|
тогда |
|
x =1−(−1) x = 2. |
|
||
|
|
|
|||
Получим пару чисел (2;−1), которая является решение исходной системы. |
|||||
Ответ: x = 2, |
y = −1. |
|
|
|
|
2.2.2. Метод алгебраического сложения (линейного преобразования)
Этот способ основан на третьем утверждении из преобразований 1‒3 о равносильности системы уравнений.
x + y =8,
Пример. Решить систему уравнений
x − y = 4.
31
Решение. Складывая и вычитая уравнения системы, получим:
2x =8 +4, |
|
2x =12, |
|
x = 6, |
|
|
|
|
|
2 y =8 −4; |
|
2y = 4; |
|
y = 2. |
Пара чисел (6;2) является решением данной системы уравнений.
Ответ: x = 6, y = 2 .
5x −3y =9,
Пример. Решить систему уравнений
2x +3y =12.
Решение. В уравнениях данной системы коэффициенты при неизвестном y − противоположные числа. Если сложить почленно левые и правые части
уравнений, то получим уравнение с одной переменной x :
5x + 2x =9 +12 ,
или
7x = 21,
откуда
x =3.
Подставив значение x в одно из уравнений данной системы, например во второе, найдем y :
2 3 +3y =12 , 3y = 6 y = 2.
Пара чисел (3;2) ‒ решения исходной системы.
Ответ: x = 3, y = 2 .
Пример. Решить систему уравнений x +2 y =5,
3x − y =1.
Решение. Умножим второе уравнение на 2 и сложим с первым получим:
x +2 y =5, |
x +2 y =5, |
|
|
|
7. |
6x −2 y = 2; |
7x = |
|
Выразим x из второго уравнения системы и подставим в первое уравнение. Откуда определим соответствующее значение y :
y = 2,x =1.
32
Итак, пара (1; 2) является решением данной системы.
Ответ: x =1, y = 2.
2.2.3. Графический способ решения линейных систем
Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты точки пересечения графиков (x0 ; y0 ) и
будут являться решением данной системы уравнений.
Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Сравните с алгебраическими условиями 1-3 на стр. 29.
x + 2y =3,
Пример. Решить графически систему уравнений
2x − y =1.
Решение. Чтобы решить графически систему уравнений, выразим в каждом уравнении y через x и составим таблицу значений (см. таблицу). Так как графиком линейного уравнения с двумя неизвестными является прямая линия, то для построения последней, достаточно двух точек.
|
|
y = 12 (3 − x) |
|
|
y = 2x −1 |
|
|
|||
|
x |
1 |
|
3 |
x |
|
0 |
|
1 |
|
|
y |
1 |
|
0 |
y |
|
−1 |
|
1 |
|
Как видно |
из рис. 2.4, |
прямые |
пересекаются |
в точке |
(1;1), значит, |
|||||
исходная система имеет единственное решение.
33
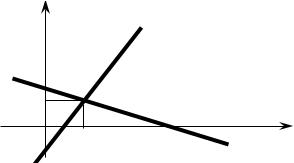
y |
y = 2x −1 |
1 |
|
y = |
1 |
(3 − x) |
||
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
х |
_ |
1 2 3 |
|
|
|||
1 |
|
|
|
|
|
|
Рис 2.4. Пересечение графиков прямых в точке (1;1)
1+2 = 3, |
3 = 3, |
‒ верно. |
|
Сделаем проверку: |
|
=1; |
|
2 −1 =1; |
1 |
|
|
Ответ: x = y =1.
Рассмотрим примеры решения систем разными методами.
4x + 2y =10,
Пример. Решить систему уравнений
6x +3y =15.
Решение. Разделим обе части первого уравнения на 2 , а второго на 3. Получим следующую систему равносильную исходной
2x + y =5,2x + y =5.
Эта система состоит из двух одинаковых уравнений. Полагая y = m , где
m R |
находим, что x = |
1 |
(5 −m) . Следовательно, решением |
последней, а |
||
|
|
2 |
|
|
|
|
значит и исходной системы является множество решений 1 |
( |
5 −m); m |
, где |
|||
|
|
|
2 |
|
|
|
m R .
Решим эту систему графически. Каждое из уравнений системы является линейной функцией. Как видно на рис. 2.5., графики этих функций совпадают. Каждую точку графика можно рассматривать как общую точку обеих прямых. Это означает, что исходная система уравнений имеет бесконечное множество
решений. Выразим x через y (из любого уравнения системы): |
x = |
1 |
(5 − y); |
|||
тогда решением системы будет любая пара чисел вида |
1 |
(5 −m); m |
|
2 |
|
|
, где m R . |
||||||
|
2 |
|
|
|
|
|
34

y
3
2
1
0 |
|
|
|
|
х |
1 2 3 |
|||||
Рис. 2.5. Две прямые, имеющие множество общих точек
Ответ: любая пара чисел вида |
1 |
(5 −m); m |
, m R . |
|
2 |
|
|
x +3y =1,
Пример. Решить систему уравнений
3x +9y =5.
Решение. Разделим второе уравнение системы на 3, получим равносильную исходной системе систему вида
x +3y =1,
x +3y = 5.3
|
Последняя |
система противоречива, поскольку не существует чисел x0 |
и |
|||
y |
таких, чтобы |
выражение x +3y |
0 |
равнялось одновременно и |
1 и |
5 . |
|
0 |
0 |
|
|
3 |
|
|
|
|
|
|
|
|
Следовательно, исходная система решений не имеет.
Графически решение данной системы представлено на рис. 2.6.
 y
y
1
0 |
|
|
х |
1 |
|||
Рис. 2.6. Графическая иллюстрация
Ответ: .
35
2.3. Методы решения нелинейных систем уравнений
2.3.1. Метод подстановки
Метод подстановки и линейного преобразования так же могут применяться и при решении нелинейных систем уравнений. Метод подстановки в основном применяется при решении тех систем, в которых в каком то уравнении одна из неизвестных входит линейно (то есть в первой степени).
|
|
xy = 2, |
|
|
|
Пример. Решить систему уравнений |
|
|
|
||
|
|
x2 + y2 =5. |
2 |
|
|
Решение. Из |
первого уравнения |
находим |
y = |
( x ≠ 0, так как в |
|
противном случае |
при x = 0 первое |
уравнение |
не |
x |
обращается в верное |
|
|||||
равенство ни при каких значениях y ), подставляя |
это выражение для y во |
||||
второе уравнение исходной системы, получим систему, равносильную исходной
y = 2 |
, |
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
4 |
|
|||
|
2 |
|
|
|
|
||
x |
|
+ |
|
x |
2 |
=5. |
|
|
|
|
|
|
|
||
Умножив второе уравнение на x2 , получим биквадратное уравнение x4 −5x2 + 4 = 0,
корнями которого являются x1 =1; |
x2 = −1; x3 = 2 ; |
x4 = −2 . |
Им соответствуют значения |
y1 = 2 ; y2 = −2 ; y3 =1; y4 = −1. |
|
Ответ: {(1;2), (−1;−2), (2;1), (−2;−1)}. |
|
|
Замечание. Если в системе при замене x ↔ y |
оно не меняется, то есть у |
|
нее будет решение (a; b) , то и (b; a) тоже будет решением.
2.3.2.Метод алгебраического сложения уравнений
Вследующем примере проиллюстрируем использование метода алгебраического сложения уравнений.
Пример. Решить систему уравнений x2 y2 − 2x2 +3xy =36,
4x2 y2 − x2 − 2xy =123.
Решение. Как видно из условия, левые части уравнений системы
36
содержат одни и те же комбинации неизвестных. Поэтому целесообразно
исключить из системы одно из неизвестных, а именно x2 . Для этого умножим обе части второго уравнения на (−2) и сложим с первым
−7x2 y2 + 7xy = −210
или
(xy)2 − xy −30 = 0 ,
Сделав замену z = xy , получим квадратное уравнение
z2 − z −30 = 0 ,
корнями которого (например, по теореме Виета) будут z1 = 6 и z2 = −5 .
Откуда
xy = 6
или
xy = −5.
Таким образом, исходная система распадается на две системы
|
|
xy = 6, |
|
xy = −5, |
|
|
|
|
36. |
|
|
|
|
x2 y2 −2x2 +3xy = |
x2 y2 −2x2 +3xy =36. |
||
Найдем решение первой системы: |
|
|
|||
1) |
xy = 6, |
xy = 6, |
xy =6, |
x = ±3, |
|
36 −2x2 |
+18 =36. x2 =9. |
x = ±3. |
y = ±2. |
||
|
|
|
|
|
|
Найдем решение второй системы: |
|
|
|||
2) |
xy = −5, |
xy = −5, |
|
|
|
|
|
|
|
|
|
|
−2x2 = 26. x2 = −13. |
|
|
|
|
Уравнение |
x2 = −13 не имеет действительных корней, а значит, вторая |
||||
система не имеет решений. Следовательно, решением исходной системы являются решение первой системы: (3;−2), (−1;−2), (3;2).
Ответ: x1 = 3, y1 = −2; x2 = −1, y2 = −2; x3 = 3, y3 = 2.
37
2.3.3. Метод разложения на множители
Нередко для понижения степени уравнений входящих в систему, используется приём разложения одного из уравнений на множители. Тогда исходную систему уравнений заменяем равносильной ей совокупностью более простых систем уравнений.
Рассмотрим применение данного метода на примерах.
x3 − y3 = 3(x − y),
Пример. Решить систему уравнений
2x2 + xy +2 y2 =10.
Решение. Преобразуем первое уравнение системы, для этого воспользуемся формулой a3 −b3 =(a −b)(a2 + ab +b2 ):
x3 − y3 −3(x − y)= 0 ,
(x − y)(x2 + xy + y2 )−3(x − y), (x − y)(x2 + xy + y2 −3)= 0.
Тогда исходная система равносильна совокупности систем
x − y = 0,
2x2 + xy +2 y2 =10;
x2 + xy + y2 −3 = 0,2x2 + xy +2 y2 =10.
Решить совокупность систем – значит найти все пары чисел (x0 , y0 ),
каждая из которых является решением хотя бы одной из систем, входящих в совокупность.
Из первой системы совокупности следует:
x = y,
5y2 =10.
Откуда получаем y1,2 = ±
 2 . Таким образом, решение первой системы совокупности являются (
2 . Таким образом, решение первой системы совокупности являются (
 2;
2;
 2 ),(−
2 ),(−
 2;−
2;−
 2 ).
2 ).
Для решения второй системы совокупности умножим первое уравнение на 2 и вычтем из него второе уравнение. Получим уравнение
xy = −4.
38

Откуда
y = − 4x .
Подставим y во второе уравнение второй системы, приходим к уравнению
x2 −7 + |
16 |
= 0 |
x4 −7x2 +16 = 0, |
|
x2 |
|
|
которое не имеет решений (проверьте самостоятельно). Следовательно, вторая система уравнений совокупности решений не имеет. Решением всей совокупности являются лишь решения первой системы.
Ответ: x1 = 
 2, y1 =
2, y1 = 
 2; x2 = −
2; x2 = −
 2, y2 = −
2, y2 = −
 2.
2.
2.3.4. Метод замены переменных
При решении систем уравнений часто применяется метод замены переменных, в результате чего получается более простая система уравнений относительно новых переменных. После решения такой системы необходимо найти значения исходных переменных.
Общего правила выбора переменных не существует. Имеется несколько видов систем, для которых можно указать подходящую замену:
1)в системах встречаются одинаковые выражения с переменными;
2)системы симметрических уравнений;
3)системы уравнений, одно из которых однородно.
Рассмотрим примеры замены переменных.
|
|
|
|
8 |
|
+ |
|
|
20 |
= 3, |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3x +2 y |
|||||||
|
|
|
x −2 y |
|
|
|
||||||
Пример. Решить систему уравнений |
12 |
|
|
|
|
40 |
|
|||||
|
|
|
|
|
|
− |
|
|
=1. |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
3x +2 y |
|
|||
|
|
|
x −2 y |
|
|
|
||||||
Решение. Обозначим |
1 |
= u, |
|
|
2 |
|
= v, |
тогда данная система |
||||
x −2 y |
3x +2 y |
|||||||||||
|
|
|
|
|
|
|
||||||
примет вид
8u +20v = 3,12u −40v =1.
Уравняем коэффициенты при v , для чего умножим обе части первого уравнения системы на 2 и сложим со 2-м уравнением:
39

16u +40v = 6,12u −40v =1.
Или
16u +12v = 7 28u = 7,
откуда
u = 14 .
Значение v найдём из первого уравнения решаемой системы:
8 14 +20v = 3,
2 + 20v = 3,
20v =1,
v = 201 .
Учитывая подстановки, получим равносильную систему уравнений для неизвестных x и y :
|
1 |
= 1 , |
|
|
||
|
|
x −2y = 4, |
||||
|
4 |
|
||||
x −2 y |
|
|||||
|
1 |
|
|
1 |
|
или |
|
|
= |
; |
3x + 2y = 20. |
||
|
|
|
||||
|
3x +2 y 20 |
|
||||
|
|
|||||
Складывая почленно левые и правые части уравнений системы, получим
x + 3x = 24,
4x = 24,
откуда
x = 6.
Тогда значение y найдём из первого уравнения исходной системы:
6 −2y = 4,
2y = 2,
откуда y =1.
Итак, пара чисел (6;2) − решение исходной системы.
Ответ: x = 6, y = 2 .
40
Многочлен называется симметрическим, если при любой перестановке входящих в него переменных получается тождественно равный ему многочлен. Если оба уравнения системы являются симметрическими многочленами от x и y , то система называется симметрической.
Вэтом случае за новые переменные обозначают
x+ y =u, x y =ν .
Если пара чисел (x0 , y0 ) является решением симметрической системе, то пара (y0 , x0 ) так же является решением системы.
Для симметричных систем полезны следующие представления:
1)x2 + y2 = (x + y)2 −2xy =u2 −2ν;
2)x3 + y3 = (x + y)(x2 − xy + y2 )= u (u2 −3ν );
3)x4 + y4 = (x2 + y2 )2 −2x2 y2 =(u2 −2ν )2 −2ν2 .
Эти выражения не обязательно помнить, но нужно уметь выводить их самостоятельно.
x2 + xy + y2 = 21,
Пример. Решить систему уравнений
x + xy + y =9.
Решение. При замене x на y , а y на x система не изменит своего вида.
Следовательно, данная система – симметрическая. Введём новые переменные x + y =u, x y =ν и выразим через них левые части уравнений
x2 + xy + y2 = (x + y)2 − xy =u2 −ν x + xy + y =(x + y) + xy =u +ν .
Тогда исходная система примет вид
u2 −ν = 21,u +ν =9.
Сложив уравнения этой системы, получим квадратное уравнение u2 +u −30 = 0.
Откуда находим u1 =5 и u2 = −6. Так как ν = 9 −u, то ν1 = 4 ν2 =15 . Таким образом, получены две пары (5;4) и (−6;15), удовлетворяющие системе
разрешённой относительно u и ν . Переходя к исходным переменным, получаем совокупность двух систем
41

x + y =5,xy = 4;
x + y = −6,xy =15.
Решая первую методом подстановки, |
|
находим (1;4), (4;1). Вторая |
||
система решений не имеет. |
|
|
|
|
Ответ: x1 =1, y1 = 4; x2 = 4, y2 =1. |
|
|
|
|
|
2 |
+ 2y |
2 |
=17, |
x |
|
|
||
Пример. Решить систему уравнений |
2 |
− 2xy = −3. |
||
x |
||||
Решение. Умножим первое уравнение на 3, а второе на 17 и сложим. Приходим к однородному уравнению
20x2 −34xy + 6y2 = 0.
Разделив его на 2y2 ( y ≠ 0, так как при y = 0 первоначальная система не имеет решений), получим квадратное уравнение относительно замены t = xy :
10t2 −17t +3 = 0.
Откуда t1 = 15 и t2 = 32.
Тогда исходная система равносильна совокупности систем
|
x |
= |
1 |
, |
||||
|
|
|
|
|
5 |
|||
|
|
|
||||||
|
y |
|
|
|||||
|
|
2 |
−2xy +3 = 0; |
|||||
x |
|
|
||||||
|
x |
|
3 |
|
||||
|
= |
, |
||||||
|
|
|
|
|
2 |
|||
|
|
|
||||||
y |
|
|
||||||
|
x2 |
−2xy +3 = 0; |
||||||
|
||||||||
|
|
|
|
|
|
|
||
y =5x,
x2 −2xy +3 = 0;
2x = 3y,
x2 −2xy +3 = 0.
Решая каждую систему известными нам методами, найдём решение системы.
Ответ: x = − |
1 |
|
, y = − |
5 |
|
; |
x |
|
= |
1 |
|
, y |
|
= |
5 |
|
; x |
= −3, y = −2; |
x |
|
= 3, y |
|
= 2. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
3 |
1 |
|
3 |
|
|
2 |
|
3 |
|
2 |
|
3 |
3 |
1 |
|
4 |
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
42

2.4. Задания для самостоятельного решения
2.1. Решить системы способом подстановки:
x = 2 + y, |
|
2. |
y =11−2x, |
|
1. |
9. |
|
8. |
|
3x −2y = |
|
5x −4y = |
||
2x + y =8, |
5. |
3x − y =5, |
||
4. |
|
|
23. |
|
3x + 4y = 7. |
|
5x + 2y = |
||
2.2. Решить системы способом сложения:
2х +11y =15, |
9x −17y = −14, |
1. |
2. |
10x −11y =9. |
−9x +15y =12. |
13x −8y = 28, |
40x +3y =10, |
4. |
5. |
11x −8y = 24. |
20x −7 y =5. |
x −3y =12,
3.2x + 4y =90.
5x +6y =13,
6.7x +8y = 21.
4x −7y =30,
3.4x −5y =90.
5x −2y =1,
6.15x −3y = −3.
2.3. Решить графически системы уравнений:
x +5y = 7, |
2. |
2x +10y =13, |
x + y =9, |
1. |
|
3. |
|
3x −2y = 4. |
|
x +2 y =5. |
x − y =3. |
x − y = 4, |
|
x + y =3, |
x +3y =14, |
4. |
5. |
6. |
|
3x + 2y = 7. |
|
2x −3y = −4. |
2y − x = 6. |
2.4. Решить системы уравнений, используя метод подстановки или метод алгебраического сложения:
1. |
3x + 4y = −3, |
2. |
5x + 2y = 25, |
|
|
||
|
y −3x =18. |
|
3x + 4y = 29. |
4. |
2x +5y =1, |
5. |
6x +5y = −8, |
|
|
||
|
4x +3y =9. |
|
4x +7y = 2. |
7. |
3x = −2, |
8. |
10x −3y = 67, |
|
|
||
|
9x + y = 2. |
|
7 y −5x = 27. |
4x +9y =1,
3. 5x −18y = −28.
x − y =14,
6. 2 3
x + y =3.
18 12
5x −3y = 4, 9. 3x + 2y = 29.
43

10. |
7x +3y =1, |
|
||||||
|
|
|
|
|
|
|||
|
14x −6y = 2. |
|
||||||
13. |
2x + y = 4, |
|
||||||
|
|
|
|
|
|
|||
|
5x −3y = −1. |
|
||||||
16. |
x − y = 4, |
|
||||||
|
|
|
|
|
|
|||
|
3x + 2y = 7. |
|
||||||
|
x + y |
+ |
|
x − y |
= −5, |
|||
19. |
|
8 |
6 |
|||||
|
|
|
||||||
|
|
x + y |
− |
|
x − y |
=10. |
||
|
|
|
4 |
|
3 |
|||
|
|
|
|
|
||||
11. |
x −3y =12, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2y +7 = 0. |
|
|
|
|
|
||||
14. |
x +3y =14, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2y − x = 6. |
|
|
|
|
|
||||
17. |
4(x + 2y) −8 =5x −2, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3(2x − y) +6 = 24y +12. |
|||||||||
|
3x +1 |
− |
2x − y |
= |
2 y − x |
, |
||||
20. |
|
7 |
|
2 |
|
|
|
8 |
|
|
|
4x −2 |
− |
|
4 y −5x |
|
= |
x + y |
. |
||
|
|
3 |
2 |
|
|
5 |
||||
|
|
|
|
|
|
|
||||
3x + y = −2, 12. 4x −6y = −10.
15. y +3x =11,2x − y =9.
5(x −3y) −6 = 2x +1, 18. 3(x +6y) + 4 =9y +19.
2.5. Решить системы уравнений:
1. |
x + 2xy + y =10, |
2. |
x +5y = 26, |
|
|
|
156. |
||
|
x −2xy + y = −2. |
|
x2 −25y2 = |
|
4. |
x + y = 6, |
5. |
x2 − xy −3y =5, |
|
|
|
|
||
|
xy =8. |
|
y −2x = 0. |
|
x2 + xy = 2,
3.y −3x = 7.
xy + x + y = 29,
6.xy − 2(x + y)= 2.
2.6. Решить систему уравнений используя метод замены переменных:
|
3 |
+ |
|
1 |
= |
2 |
, |
||
|
|
|
|
|
|||||
2x + y |
2x − y |
5 |
|||||||
1. |
|
|
|
|
|||||
|
|
7 |
+ |
|
2 |
= 3. |
|||
|
|
|
|
||||||
|
2x + y |
|
|
2x − y |
|
5 |
|
||
|
|
|
|
|
|||||
x + y + x − y =13, 4. x − y x + y 6
xy =5.
|
|
3 |
|
|
− |
|
|
2 |
= |
11 |
, |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
− xy |
y |
2 |
− xy |
|
|
|
|||||||||
2. x |
|
|
|
|
|
|
12 |
|
|
|||||||||
|
|
|
4 |
|
|
+ |
|
|
3 |
|
= − |
2 |
. |
|||||
|
|
2 |
− xy |
|
y |
2 |
− xy |
|
3 |
|||||||||
x |
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
+ y = 2, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
5. x |
+ 2y |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y |
= −3. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x + 2y |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x + y = 34 , 3. y x 15
x2 + y2 =34.
4xy − xy =30,
6.
x
3xy + 2 y = 28.
|
|
|
2.7. Решить симметрические системы уравнений: |
|
|
|
||||||||
1. |
|
|
2 + |
y |
2 = |
34, |
2. |
x +3xy + y =9, |
3. |
x3 |
+ y3 |
= 7, |
||
x |
|
|
|
x2 |
+ y2 + xy = 7. |
|
|
|
||||||
|
|
x + y + 2xy =38. |
|
|
|
(xy +5)(x + y)=3. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
44
4. |
x |
+ xy + y =11, |
|
5. |
(x2 + y2 )xy = 78, |
6. |
2x + 2y − xy = 6, |
|||||||||||||||||||
|
2 y + xy2 =30. |
|
|
|
|
+ y4 =97. |
|
|
|
2 + y2 −3xy =5. |
||||||||||||||||
|
x |
|
|
x4 |
|
|
|
|
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.8. Решить системы уравнений, левые части которых однородны |
|||||||||||||||||||||||
относительно x и y : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1. |
|
|
2 |
+ xy −6y |
2 |
= 0, |
2. |
|
2 |
−3xy + y |
2 |
= −5, |
3. |
|
2 |
−3xy + y |
2 |
= −1, |
||||||||
2x |
|
|
x |
|
|
x |
|
|
||||||||||||||||||
|
x2 |
−4xy +3y2 = −3. |
|
2x2 |
− xy + 2y2 = 20. |
|
3x2 − xy +3y2 =13. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
2 |
−5y |
2 |
= −1, |
|
|
|
|
|
2 |
−4xy + |
3x |
2 |
=17, |
6. |
|
|
2 |
+2xy + y |
2 |
= 20, |
||||
x |
|
|
|
5. 2 y |
|
|
5x |
|
|
|||||||||||||||||
|
3xy +7 y2 =1. |
|
|
y2 |
− x2 =16. |
|
|
|
x2 |
+2xy +2 y2 = 25. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
Пусть дано m неравенств f1(x) > g1(x) , f2 (x) > g2 (x) ,…, fm (x) > gm (x). Обозначим через M область, являющуюся пересечением областей допустимых
значений всех этих неравенств, если стоит задача: найти все числа α из области M , каждое из которых является решением каждого из этих неравенств, то говорят, что дана система неравенств
f (x) > g (x), |
|
|
1 |
1 |
|
f2 (x) > g2 (x), |
(3.1) |
|
....................... |
||
|
|
|
fm (x) > gm (x).
Область M называется областью допустимых значений (ОДЗ) этой системы.
Число α из ОДЗ системы неравенств (3.1) называется решением этой системы, если оно является решением каждого из неравенств.
Решить систему неравенств (3.1) – это значит найти множество всех ее решений. Если это множество оказывается пустым множеством, то система неравенств (3.1) не имеет решений.
Решают систему неравенств (3.1) обычно следующим образом. Сначала находят решение каждого неравенства на ОДЗ этой системы, то есть находят
N1, N2 ,..., Nm |
− множества |
всех решений |
соответствующих неравенств |
fi (x) > gi (x) |
(i =1, 2,K ,m) , |
принадлежащих |
области M. Затем находят |
45
множество N0 , являющееся пересечением всех этих множеств N1, N2 ,..., Nm , то есть N0 = N1 ∩ N2 ∩... ∩ Nm . Множеством всех решений системы неравенств (3.1) и будет множество N0 .
Пусть числа а и b таковы, что a <b и пусть задана системы неравенств
f (x) > a, |
(3.2) |
|
|
f (x) < b; |
|
Тогда систему неравенств (3.2) можно записать в виде |
двойного |
неравенства: |
|
a < f (x) <b. |
(3.3) |
Отметим, что если y = f (x) − основная элементарная функция, то часто проще решить двойное неравенство (3.3) чем систему неравенств (3.2).
Пусть теперь дано k систем неравенств
f11(x) > g11(x),f21(x) > g21(x),
.........................
fn1(x) > gn1(x),
f |
(x) > g (x), |
f |
(x) > g |
(x), |
|
12 |
12 |
1k |
1k |
|
|
f22 (x) > g22 (x), |
f2k (x) > g1k (x), |
(3.4) |
|||
......................... |
......................... |
||||
|
|
|
|
|
|
|
|
|
(x) > glk (x). |
|
|
fm2 (x) > gm2 (x), |
flk |
|
|||
Обозначим через Q область, являющуюся пересечением областей
допустимых значений всех этих систем неравенств.
Если стоит задача: найти в области Q все числа α , каждое из которых
является решением хотя бы одной из этих систем, то говорят, что дана совокупность k систем неравенств и область Q называется областью
допустимых значений (ОДЗ) этой совокупности.
Число α из ОДЗ совокупности систем неравенств (3.4) называется решением этой совокупности, если оно является решением хотя бы одной системы неравенств из совокупности (3.4).
Решить совокупность систем неравенств (3.4) – это значит найти множество всех ее решений. Если это множество оказывается пустым множеством, то совокупность систем неравенств (3.4) не имеет решений.
Совокупность систем неравенств (3.4) обычно решают следующим образом. Сначала решают каждую систему неравенств на ОДЗ совокупности (3.4), т.е. находят M1, M2 ,..., Ml ‒ множество всех решений системы
46
f |
(x) > g |
(x), |
|||
1l |
1l |
|
|
|
|
f2l (x) > g2l (x), |
|||||
........................ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fpl (x) > gpl (x); l =1, k; p =1, n |
|||||
в области Q . Затем находят множество M0 , являющееся объединением всех
этих множеств |
M0 = M1 M2 ... Mk . Тогда множество |
M0 |
и будет |
множеством всех решений совокупности систем неравенств (3.4). |
|
||
Заметим, |
что если каждая из k систем совокупности |
(3.4) |
содержит |
только одно неравенство, то говорят, что дана совокупность k неравенств. |
|||
При k =1 |
совокупность (3.4) является обычной системой неравенств. |
||
Пример. Решить систему и совокупность неравенств:
4x −3 ≥5, |
4x −3 ≥5, |
a) 5x −2 >10; |
б) 5x −2 >10. |
|
|
Решение. а) очевидно, что ОДЗ: |
x R . Из первого неравенства системы |
имеем |
|
4x ≥5 +3,
4x ≥8 , x ≥ 2.
Решая второе неравенство системы, получим
5x >10 + 2 ,
5x >12, x > 2,4 .
Получили равносильную систему неравенств:
x ≥ 2,
x > 2,4..
Отметим полученные промежутки на координатной прямой в виде штриховки (рис. 3.1), причем решение I неравенства отметим над прямой, а II - под прямой:
2 |
2,4 |
х |
|
||
Рис. 3.1. Иллюстрация решения системы |
x ≥ 2, |
|
|
||
|
|
x > 2,4. |
47
Тогда решением системы неравенств будет пересечение множеств решений неравенств системы x > 2,4 .
б) решением совокупности неравенств является объединение решений неравенств совокупности, т.е. промежуток, на котором имеется хотя бы одна штриховка. Из рис. 3.1 видно, что решением совокупности неравенств б) является полуинтервал x ≥ 2.
Ответ: а) x (2,4;+∞) ; б) x [2; + ∞).
Замечание. Если в системе, состоящей из нескольких неравенств, одно является следствием другого (или других), то неравенство-следствие можно отбросить.
2x −3 > x +0,5,
Пример. Решить систему неравенств 4 −3x >5 −4x,
0,5x +1< x.
Решение. Из I неравенства системы имеем
2x − x > 0,5 + 3 ,
или
x > 3,5 ;
из II неравенства получим −3x + 4x >5 −4 , откуда x >1.
Наконец, из III неравенства имеем
x − 0,5x >1
или
0,5x >1,
откуда
x > 2.
Следовательно, получили равносильную систему
x >3,5,
x >1,x > 2.
Откуда x > 3,5 − решение исходной системы.
Ответ: x (3,5; +∞).
48

|
5 + x |
<1 |
|
9 − x |
, |
|||||
2 − |
|
7 |
|
− |
|
14 |
||||
Пример. Решить систему неравенств |
|
|
|
60 |
|
|||||
|
|
1 |
|
47 − |
|
> 3. |
||||
12 − |
3 |
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Решение. Упростим I неравенство системы, для чего умножим обе части на 14:
28 − 2(5 + x) <14 −(9 − x) ,
или
28 −10 −2x <14 −9 + x ,
или
−3x < −13,
откуда
x >133 .
или
или
или
оси
Упростим II неравенство системы:
12 − 473 + 13 60x >3,
20x > 473 −9,
20x > 203 ,
1x > 13 ,
33−xx > 0,
3 −x x > 0.
Получили равносильную систему неравенств
x >13,
3 (3.5)
3 − x > 0.x
Решим неравенство 3 −x x > 0 методом интервалов. Отложим на числовой x1 = 3, x2 = 0 и определим знаки в каждом из интервалов (рис. 3.2).
49

+
0 |
3 |
х |
|
|
|
||
Рис. 3.2. Иллюстрация решения неравенства |
3 − x |
> 0 |
|
|
|
x |
|
Т.о. все множество решений неравенства 3 −x x > 0 заключено в интервале
0 < x <3.
Тогда решением системы (3.5), а значит, и данной системы неравенств будет пересечение соответствующих множеств решений.
Как видно из рис. 3.3, эти множества не пересекаются, значит, система (3.5), а, следовательно, и данная система решений не имеет.
0 |
3 13 / 3 |
х |
|
Рис. 3.3. Пересечение множеств решений системы неравенств (3.5)
Ответ: .
|
|
|
|
|
|
2 |
+ |
2x −4 |
|
|
|
|
|
|
x |
|
< 2, |
||||
|
|
|
|
|
|
x |
||||
Пример. Решить систему неравенств |
|
|
|
|
|
|||||
|
|
|
|
|
2 |
≤ |
16. |
|
||
|
|
|
x |
|
|
|
||||
Решение. Упростим I неравенство системы: |
|
|||||||||
|
|
x2 + 2x − 4 |
− 2 < 0, |
|
|
|||||
|
|
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 2x − 4 − 2x |
< 0 , |
|
|||||||
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x2 x− 4 < 0
или
(x − 2)(x + 2) < 0. x
Проиллюстрируем метод интервалов для полученного неравенства на рис. 3.4.
50
|
+ |
+ |
−2 |
0 |
2 х |
Рис. 3.4. Иллюстрация решения неравенств (x −2)(x + 2) < 0 x
Множество решений для данного неравенства соответствует интервалам: x < −2, 0 < x < 2.
Решим теперь II неравенство системы: x2 −16 ≤ 0 или (x − 4)(x + 4) ≤ 0, x1 = 4, x2 = −4. Решением II неравенства системы будет отрезок −4 ≤ x ≤ 4
(рис. 3.5).
+ |
− |
+ |
−4 |
4 |
х |
Рис. 3.5. Иллюстрация решения неравенства (x − 4)(x + 4) ≤ 0 |
||
Отметив найденные решения |
I и II |
неравенств на общей числовой |
прямой, найдем пересечение решений исходной системы неравенств (рис. 3.6).
− |
4 |
− |
2 |
0 |
2 |
4 |
х |
|
|
|
|
Рис. 3.6. Иллюстрация решений исходной системы неравенств
Множества решений имеют пресечения на интервалах
−4 ≤ x < 2; 0 < x < 2.
Ответ: −4 ≤ x < 2; 0 < x < 2.
x +3 < 2,3 − x
Пример. Решить систему неравенств x3 <16x,
4 ≥ x2.
Решение. Преобразуем I неравенство системы:
3x −+x3 −2 < 0,
51

или
x +3 −6 + 2x < 0 ,
3 − x
3x −3 < 0,
3 − x
3(x −1) > 0 . x −3
или
xx −−13 > 0.
Геометрическая иллюстрация метода интервалов для данного неравенства показана на рис. 3.7.
+ |
+ |
|
1 |
3 |
х |
Рис. 3.7. Иллюстрация решения I |
неравенства |
|
Решением данного неравенства является: x <1, x > 3. Решим II неравенство заданной системы
x3 −16x < 0 .
Преобразуем его к виду
x (x −4)(x + 4)< 0,
и используя метод интервалов, определим решение (рис.3.8).
+ |
|
+ |
|
−4 |
0 |
4 |
х |
Рис. 3.8. Иллюстрация решения II неравенства |
|||
Как видно из рис. 3.8, x < −4, |
|
0 < x < 4, |
x > 4 являются решением |
неравенства x (x −4)(x + 4)< 0.
Наконец, решим III неравенство системы
4 ≥ x2
52

или
x2 −4 ≤ 0,
(x −2)(x + 2) ≤ 0.
Решением является отрезок −2 ≤ x ≤ 2 (рис. 3.9).
+ +
−2 |
2 |
х |
|
Рис. 3.9. Иллюстрация решения III неравенства
Отметив найденные решения неравенств на общей числовой прямой (рис. 3.10), найдем пересечение полученных решений.
−4 |
−2 |
0 |
1 |
2 3 4 х |
Рис. 3.10. Пересечение полученных решений
Ответ: 0 < x <1.
Пример. Решить двойное неравенство −2 <5 +3x ≤ 6 . Решение. Данное неравенство равносильно системе
5 +3x > −2,5 +3x ≤ 6,
3x > −2 −5,3x ≤ 6 −5,
3x > −7,3x ≤1,
x > −73 ,x ≤ 1 ,3
откуда −73 < x ≤ 13 .
53

Замечание. Этот пример проще решить напрямую как двойное неравенство:
−2 < 5 + 3x ≤ 6, −2 −5 < 3x ≤ 6 −5,
−7 < 3x ≤1,
или
|
|
|
− |
7 |
< x ≤ |
1 . |
|
|
|
|
|
7 |
|
1 . |
3 |
|
3 |
|
|
|
|
Ответ: − |
< x ≤ |
|
|
|
|
|
|
|
||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 ≥100x, |
|
|||
Пример. Решить совокупность неравенств |
(x +9)(7x − x2 −13) |
≥ 0. |
||||||||
|
|
|
|
|
|
|
x |
2 |
−18x +45 |
|
|
|
|
|
|
|
|
|
|
||
Решение. Упростим первое неравенство совокупности:
x(x2 −100)≥ 0,
или
x(x −10)(x +10)≥ 0, x1 = 0, x2 =10, x3 = −10.
Отрезок 10 ≤ x ≤ 0 является решением данного неравенства (рис. 3.11).
+ |
|
|
+ |
−10 |
0 |
10 |
х |
Рис. 3.11. Иллюстрация решения I неравенства
Упростим второе неравенство совокупности:
(x +9)(7x − x2 −13) |
≥ 0, |
|
x2 −18x + 45 |
|
|
или |
|
|
(x +9)(x2 −7x +13) |
≤ 0 . |
|
x2 −18x + 45 |
|
|
Заметим, что x2 −7x +13 >0 при любом |
x R , так как D < 0 |
и a =1 > 0. |
Кроме того, так как по теореме Виета, корни знаменателя x1 =15 и |
x2 = 3, то |
|
x2 −18x + 45 = (x −15)(x −3),
54

следовательно, разделив обе |
части неравенства на x2 −7x +13, получим |
|||
равносильное неравенство: |
|
|
|
|
|
x +9 |
|
|
|
|
|
≤ 0. |
|
|
|
(x −15)(x −3) |
|
|
|
На рис. 3.12 проиллюстрировано решение второго неравенства x ≤ −9 и |
||||
3 < x <15. |
|
|
|
|
+ |
|
|
+ |
|
−9 |
3 |
|
15 |
х |
|
|
|||
Рис. 3.12. Иллюстрация решения II |
неравенства |
|||
Объединяя найденные решения каждого из неравенств в совокупности, получим
−10 −9 |
0 |
3 |
10 15 |
х |
|
Рис. 3.13. Решение данной совокупности неравенства
Полуинтервалы |
(−∞;0] (3;15) (15; + ∞) удовлетворяют решению |
данной совокупности неравенств. |
|
Ответ: x ≤ 0, |
3 < x <15, x >15. |
3.1. Задания для самостоятельной работы
3.1. Решить систему неравенств:
1. |
1< 2x −1< 9, |
|
2. |
x2 |
≥ 9, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
−1 ≤1− x ≤ 4. |
|
|
0 < 2x +9 <17. |
|||||||||||
|
0 < (x −2)2 < 25, |
|
|
|
|
4 |
|
|
|
|
<1, |
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(x −2) |
2 |
|
|||||||||||
4. x2 |
+4x +4 |
≥ |
0. |
5. |
|
|
|
||||||||
|
|
|
|
|
|
|
x2 |
≥ |
1. |
||||||
|
|
x +1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
−1 |
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||
|
9 |
≥1, |
|
||||
|
|
|
|
||||
3. x2 |
|
|
|
|
|||
|
1 |
|
|
≤ 0. |
|
||
|
|
|
|
|
|
||
x −2 |
|
|
|||||
|
|
|
2 |
> 0, |
|||
1− x |
|
|
|||||
6. |
|
|
|
|
|
|
|
|
x −1 |
|
+ 1 |
> 0. |
|||
|
|||||||
|
2 − x |
2 |
|
||||
55
4x2 +5x −6 > 0, 7. x > 0.
10.x2 −4x < 0,x2 − x −6 ≥ 0.
|
|
1− x |
2 |
|
≥ 0, |
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|||
13. x |
|
+2x −8 |
|
|
|
|||
(x +2)(x2 −2x +7) |
≤ 0. |
|||||||
|
|
|
9 |
− x |
2 |
|||
|
|
|
|
|
||||
2x −1 >5x −4, 16. 8x +6 > 3x −4,
11x −9 <15x +3.
|
|
4 |
|
|
4 |
|
x + |
3 |
≥ |
3 x, |
|
19. |
|
|
|
|
|
9x2 −9x +1< 0, |
|||||
|
|
1 |
|
|
|
|
1 > |
|
|
. |
|
|
3x |
|
|||
|
|
|
|
||
8. x |
|
−2x −8 < 0, |
9. (x |
|
|
|
+1)(x |
|
−2)≥ 0, |
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
||
x2 +4x −5 > 0. |
|
x < 3. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +1 > 0, |
|
|
|
|
|||||||||
|
|
|
2 |
−144 > 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11. |
|
|
12. 1 |
− x > 0, |
|
|
|
||||||||||||||
x |
|
|
|
|
|||||||||||||||||
|
x −3 < 0. |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
4 < 0. |
|
|
||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x −3 >8 −3x, |
x −2 |
|
+ |
x |
≥ |
3 −2x |
, |
|
||||||||||||
14. |
|
3 |
|
|
|
|
|
|
15 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||
|
6 − x < 9 +4x. |
|
5x −1 |
|
|
7x |
|
|
1−3x |
|
|||||||||||
|
|
|
|
|
|
|
|
− |
≤ |
. |
|||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
12 |
|
|||||
|
2x +3 < 2, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
(x −5)< 0, |
|
|
||||||||||||||||
17. 3x −2 |
18. |
x +4 |
|
|
|
|
|
|
|||||||||||||
|
|
x +3 |
|
<1. |
|
|
≤ |
0. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x −2 |
|
|
|
|
|
|
||||||||
|
x −3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
20. |
(x2 +12x +35)(1+2x)(3−2x)≥0, |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
−2x −8)(1− |
2x)≤0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2. Решить совокупность неравенств:
1. |
−1< x <1, |
2. |
0 < x ≤ 3, |
||
|
|
|
|
||
|
0 ≤ x ≤5. |
|
−2 ≤ x ≤ 0. |
||
4. |
−1< 2x −1<1, |
5. |
1< 3x −2 ≤ 4, |
||
|
|
|
|
||
|
0 < x +2 < 4. |
|
−3 < 4x +5 <1. |
||
7. |
2x −1 > 3, |
8. |
x2 −2x −8 < 0, |
||
|
|
2 |
+4x −5 > 0. |
||
|
3x −2 ≥11. |
|
x |
|
|
|
3x −5 <1, |
|
3x −2 > 4, |
||
10. |
11. |
|
|
||
|
2x +3 > 4. |
|
4x −8 ≥16. |
||
x < 2, 3. x >1.
5x +6 ≤1, 6. 2x +1 ≥ 3.
x > 2,
9. x ≥ 13.3
12.4 − x2 ≥ 0,
x2 −4x +3 ≥ 0.
56
