Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1439

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.16 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

	π	π
	2	2
3.	∫sin n x ×sin n x d x .	4. ∫ cos n x sin n x d x .
	0	0
	1	1
5.	∫ x m (1 - x ) n d x .	6. ∫ x m× ln n x d x .
	0	0
	1
7.	∫ (1 - x 2 ) n d x . Используя результат вычисления, получить следующую
	0

формулу суммирования:

n	(-1)	k		( 2 n )!!
∑			C nk =		,
	2k +1
k =0				( 2n +1)!!
где C nk - биномиальные коэффициенты.
Утверждение 2. ( Замена переменной в определенном интеграле). Ес-
ли функция f ( x ) непрерывна на отрезке [а ; b] , а функция ϕ(t )						непрерывна
вместе со своей производной ϕ ' ( t ) на				отрезке [ α ; β ] , причем		ϕ(α) =a ,
ϕ(β) =b , то справедливо равенство			β
b
∫ f ( x ) d x = ∫ f ( j (t )) j¢( t ) dt .
a			α

Некоторые следствия из утверждения 2

В случае, когда подынтегральная функция положительна на отрезке интегрирования, приводимые ниже утверждения допускают наглядную геометрическую иллюстрацию.

а) Интеграл от «сдвинутой» функции.

Если функция f ( x) интегрируема на отрезке[ a;b ], то «сдвинутая» функ-

ция f ( x − h ) интегрируема на отрезке [a + h; b + h]		и справедливо равенство
(рис.1.5.)	b+h
b	b+h
∫	f ( x ) d x = ∫ f ( x - h ) d x.	(1.5)
a	a+h

Рис. 1.5.

б) Интеграл от периодической функции.
Если периодическая с периодом T функция		f ( x) интегрируема на пе-
риоде, то справедливо соотношение (рис. 1.6.)
a+T	T
∫	f ( x ) d x =∫ f ( x ) d x a R.	(1.6)
a	0

Рис. 1.6.

в) Интеграл от «сдвинутой и деформированной» функции.

Если функция f ( x) непрерывна на отрезке [ a;b ] , то имеет место равенство (рис. 1.7.)

b	1
∫	f ( x ) d x =( b − a ) ∫ f (a + ( b − a ) x)d x.	(1.7)
a	0

Рис.1.7.

г) Интеграл от функции f ( x) , «отраженной» относительно прямой

x = a + b (рис. 1.8.)

b	b
∫	f ( x ) d x =∫ f ( a + b − x ) d x.	(1.8)
a	a
	22

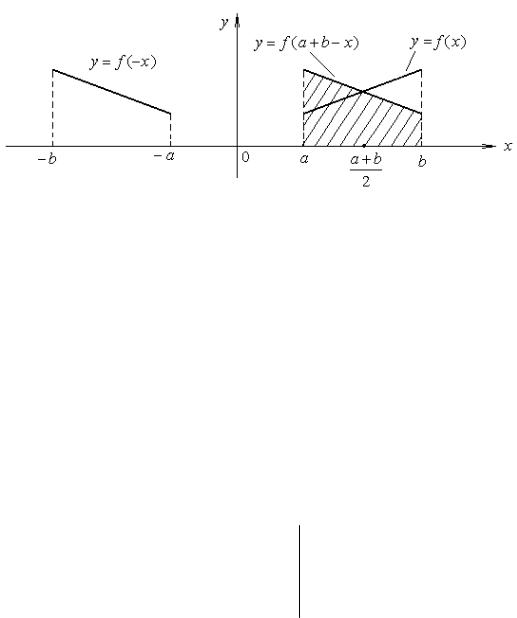
Рис.1.8.

Упражнение. Доказать соотношения а, б, в, г.

Примеры решения задач

Пример 1.15. Доказать, что если f ( x) [0;1] , то

	π	π
	2	2
1)	∫ f (sin x ) d x =∫ f (cos x) d x ;
	0	0
2)	π		π π
2)	∫ x f (sin x ) d x =		2	∫ f (sin x) d x.
	0		2	0
	0			0

Решение

π	π
2	2

1) ∫ f (sin x ) d x =∫

0 0

π
cos		− x d x =
	2

π − x = t; d x = −d t.
π − x = t; d x = −d t.
2	; x = π		=
x = 0 →t = π	; x = π	→t = 0.
2	2

	π	π
0	2	2
= −∫ f (cost) dt =∫ f (cost) d t = ∫ f (cos x) d x.
π	0	0
2

π	π				π − x = t;	d x = −d t,	=
π	π
2) I = ∫ x f (sin x ) d x = ∫ x f (sin(π − x ) d x =
0	0				x = 0 → t = π; x = π → t = 0.
0	0
0	π			π		π
= −∫ (π − t) f (sin t) d t = π ∫ f (sin t ) d t − ∫ t f (sin t ) d t = π ∫ f (sin x ) d x − I.
π	0			0		0
π	f (sin x) d x и	I =	π	π
Отсюда 2 I = π ∫	f (sin x) d x и	I =	2	∫ f (sin x) d x.
0			2	0
0				0

Замечание. Равенства 1 и 2 примера 1 являются частными случаями ра-

венства из пункта г, первое при a = 0, b = π , второе при a = 0, b = π.

В следующем примере мы покажем, что соотношения, подобные приведенным в примере 1 справедливы и в более общем случае.

Пример 1.16.	Пусть				функция ϕ(x) [ 0;l ] и удовлетворяет условию
ϕ(l − x ) = ϕ( x ), а функция					f ( x ) непрерывна на образе ϕ( [0;l ] ) отрезка [ 0;l ] .
Доказать, что
				l
l
l	2
1 ) ∫ f ( ϕ ( x ) ) d x = 2 ∫ f ( ϕ ( x ) ) d x ,
0	0
l			l		l
2) ∫ x f ( ϕ ( x ) ) d x =			l		∫ f ( ϕ ( x ) ) d x .
2) ∫ x f ( ϕ ( x ) ) d x =					∫ f ( ϕ ( x ) ) d x .
0	2				0
0					0
Решение.
		l
l						l
l	2					l
1) ∫ f ( ϕ ( x ) ) d x = ∫ f ( ϕ ( x ) ) d x + ∫ f ( ϕ ( x ) ) d x =
0	0					l
					2

=	x = l − t ; t = l − x , d x = −dt

	x =	l	→ t =	l	; x = l	→ t = 0


	2		2

= ∫ f ( ϕ ( x ) ) d x − ∫ f ( ϕ (l − t ) ) dt =

l		l		l
2		2		2

= ∫ f ( ϕ ( x ) ) d x + ∫ f ( ϕ ( t ) ) d t = 2∫ f ( ϕ ( x ) ) d x.

0	0	0
l		x = l − t ; d x = −dt		=
l
2) ∫ x f ( ϕ ( x ) ) d x =
0		x = 0 → t = l ; x = l →t = 0
0
0		l	l

= −∫ ( l − t ) f ( ϕ (l − t ) ) dt = l ∫ f ( ϕ ( t ) ) d t − ∫t f ( ϕ ( t ) ) d t.

Перенося второе слагаемое в левую часть и деля на два, получаем равенство 2.

Рекомендуем рассмотреть геометрическую интерпретацию полученных соотношений.

Пример 1.17. Функция f ( x ) непрерывна на R и x R

x+T

∫ f ( t ) ) d t = ∫ f ( t ) ) dt.

	x	0
Доказать, что f ( x ) - периодическая с периодом T функция.
Решение. Из условия задачи имеем
x+T	T
Ф( x ) = ∫ f ( t ) dt − ∫ f ( t ) dt ≡0 x R .
x	0
Отсюда
Ф′ ( x ) = f (x + T ) − f ( x ) ≡ 0 .
Или f (x + T ) = f ( x )	x T , а это означает , что f ( x ) – периодиче-

ская с периодом Т функция.

Пример 1.18. Доказать, что: а) любая первообразная нечетной функции является четной функцией; б) среди первообразных четной функции есть, и

притом только одна, нечетная функция.
Решение . Если функция f ( x )		интегрируема на симметричном проме-
жутке Х, то любая ее первообразная на этом промежутке имеет вид
	x
	F ( x ) = ∫ f ( t ) d t + C, a X .
	a
а) Пусть функция	f ( x ) – нечетная , то есть f (− x ) = − f ( x ) , тогда
− x		t = − y ; dt = −d y		=

F (−x ) = ∫ f ( t ) dt + C =
a		t = a → y = −a ; t = −x → y = x

x	a	x	x
− ∫ f (− y ) d y + C = ∫ f ( y ) d y + ∫ f ( y ) d y + C = ∫ f ( y ) d y + C = F (x) .
−a	−a	a	a
Итак, получим F ( − x ) = F ( x )		при любом С, а это означает, что F ( x )-

четная функция					f (−x ) = f ( x ) , тогда
б) Пусть функция f (x) –		четная, то есть			f (−x ) = f ( x ) , тогда
	− x				x
F (−x ) = ∫ f ( t ) d t + C =			t = − y	= − ∫ f (− y ) d y + C =
F (−x ) = ∫ f ( t ) d t + C =			t = − y	= − ∫ f (− y ) d y + C =
	a				−a
a	x		x		a
= − ∫ f ( y ) d y − ∫ f ( y ) d y + C = −∫ f ( y ) d y + C − 2∫ f ( y ) d y.
−a	a		a		0

Отсюда следует, что только при единственном выборе C = 2∫ f ( y ) d y

выполняется условие F (−x ) = −F ( x ) нечетности функции F ( x ).

Задачи для самостоятельного решения

1. Доказать равенство

1		1
∫ 4	1 − x 4	d x = ∫ 4	1 − ( x −1)4	d x.
0	0

Вычислить интеграл

sin x

cos x

∫

x d x .

+ cos

1 + sin

Функция f ( x ) непрерывна на отрезке

≤

a 2 + b 2

. Доказать, что

2π

∫ f ( a cos x + b sin x ) d x = 2∫ f (

a 2 + b2

cos x ) d x.

Функция f ( x ) – непрерывная периодическая с периодом T. Доказать,

что функция F ( x ) = ∫ f ( x ) d x

в общем случае есть сумма линейной и перио-

дической с периодом T функций. Найти условие того , чтобы F ( x ) была периодической с периодом T.

Рассмотрим далее вычисление интегралов в симметричных пределах

Утверждение 3. Если интегрируемая на отрезке [ − a; a ] функция		f ( x )
четная, то есть f ( − x ) = f ( x ) x [−a; a ], то
a	a
∫ f (x) d x = 2 ∫ f (x) d x,		(1.9)
−a	0
если f ( x ) - нечетная функция, то есть f ( − x ) = − f ( x ) x [−a; a ], то
a
∫ f (x) d x = 0.	(рис. 1.9)	(1.10)
−a

Упражнение. Доказать утверждение 3.

Рис. 1.9.

Известно, что любую функцию

f ( x ) , определенную на симметричном

промежутке, можно представить в виде

f (x) = f ч (x) + fн (x),

где

f (x) + f (− x)

f (x) − f (− x)

f ч (x) =

fн (x) =

Функцию f ч (x) называют четной, а

fн (x) -

нечетной частью функции

f ( x ) .

Используя такое представление и утверждение 1, получаем

∫ f (x) d x = ∫ fч (x) d x + ∫ fн (x) d x = ∫ fч (x) d x = 2 ∫ fч (x) d x.

−a

Итак, имеет место соотношение

∫

f (x) d x = 2 ∫ f ч (x) d x.

(1.11)

−a

d x

Пример 1.19. Вычислить интеграл ∫

−1 1 + x 3 + 1 + x 6

Решение. Здесь

f (x) =

, а ее удвоенная четная часть

1+ x 3 + 1+ x 6

2 × f ч (x) =

1 - x 3 + 1 + x 6

1 + x 3 + 1 + x 6

2 (1 +

)

1 - x 3

+ 1 + x 6 +1 + x 3 + 1 + x

1 + x

= 1.

(1 +

)2 - (x3 )2

1 + 2 1 + x 6 +1 + x6 - x6

1 + x 6

Согласно формуле (1.11) получаем

d x

∫

= ∫1× d x = x

10 = 1.

−1 1 + x 3

+ 1 + x 6

Замечание. Конечно, этот интеграл можно вычислить и без использова-

ния

соотношения

(1.11),

разбивая

отрезок

интегрирования

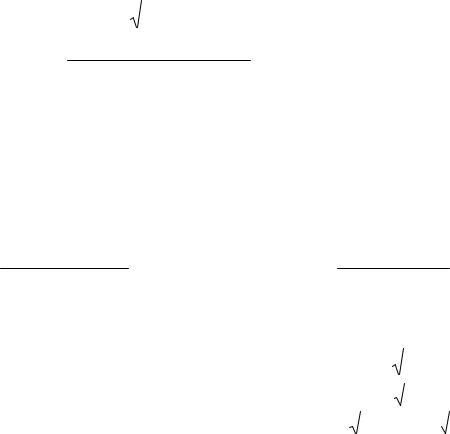
[-1; 1] = [-1; 0] U [0; 1] и производя в интеграле по отрезку [-1; 0] замену пере-

менной x на – x. (Рекомендуем проделать это читателю).
Утверждение 4. Пусть	f ( x ) – четная функция, а функция ϕ( x) удовле-
творяет условию ϕ( x ) + ϕ( − x ) = C, тогда справедливо соотношение
a	a
∫ ϕ (x) f (x) d x = C ∫ f (x) d x.		(1.12)
−a	0

Упражнение. Доказать соотношение (1.12).

Замечание. Функция φ( x), удовлетворяющая условию ϕ( x ) + ϕ( − x ) = C

, имеет график, симметричный относительно точки с координатами (0; C/2). Ниже приведены примеры таких функций.

ϕ( x ) =	1		,		α R, b > 0,
ϕ( x ) =		1 + bd x	,		α R, b > 0,
ϕ( x ) =				1		, n − нечетноечисло,

	1 + x n +
	1 + x n +				1 + x 2 n

ϕ ( x ) = ln ( b − x )α , α R, ln ( b − x )α + ln ( b + x )α

ϕ( x ) = arcctgx.

Задачи для самостоятельного решения

Вычислить интегралы

	1					d x
	−∫1					d x
1.	−∫1		(eα x + 1 )(1 + x 2 ).
	1						2 + x
3.	∫ sin 2 x ln						2 + x		d x.
3.	∫ sin 2 x ln								d x.
	−1						2 − x
	−1
	π
	4			arcctg x
5.	∫							d x.
5.	∫			cos	2			d x.
	−	π		cos		x
	−	4
		4

d x

∫π

(2 x + 1 )cos 2 x

−

x 2 d x

= 2 k − 1.

∫

, n

+ x n

−1 1

+ 1 + x 2 n

ln 3 3 − x

∫

d x.

−1 ln 3 3

+ x + ln 3 3 − x

Примеры решения различных задач

1	ln (1 + x)
Пример 1.20. Вычислить интеграл ∫			d x.
	1 + x	2
0

Решение.

1	ln (1 + x )		x = tg t,
1	ln (1 + x )	d x =	x = 0 → t = 0,
∫		d x =	x = 0 → t = 0,
∫	1 + x 2
0			x = 1 → t = π .
			x = 1 → t = π .
			4

π		π		sin t + cos t
4		4
= ∫	ln (1 + tg t ) dt =∫		ln		dt =
= ∫	ln (1 + tg t ) dt =∫		ln		dt =
0		0		cos t
0		0
	π	π

										p		1			4		4					p


	=		sin t + cost =			2		sin t	+		=			ln 2 ∫ dt +			∫ ln sin t +					d t -
	=		sin t + cost =			2		sin t	+	4	=	2		ln 2 ∫ dt +			∫ ln sin t +					d t -
										4		2			0		0					4
					π										0		0
															p

					4
					- ∫ ln cost dt =				Замена				t =		4 - y			=
					0				во втором						интеграле
							π								π
	=				p	4			p						4					p
	=				ln 2	+ ∫ ln sin			2	- y d y -∫ ln cos t dt =										ln 2.
					8	0			2						0					8
						0									0
												1		arctg x
	Пример 1.21. Вычислить интеграл ∫													arctg x		d x.
	Пример 1.21. Вычислить интеграл ∫															d x.
												0		1 + x
												0
	Решение. Проведем интегрирование по частям
1		arctg x			1														1	1	ln (1 + x )
∫				d x = ∫ arctg x d ( ln (1 + x ) ) =arctg x × ln (1 + x )															0	- ∫				d x =
																					1	+ x	2	d x =
																							2
0		1 + x			0															0

= π ln 2 − π ln 2 = π ln 2. 4 8 8

Здесь использовалось значение интеграла, вычисленного в предыдущем примере.

Пример 1.22. Вычислить интеграл 2 min {x , max{1; x} }d x .

∫ 2

−2

Решение. Легче всего записать подынтегральную функцию, нарисовав ее график (рис. 1.10.)

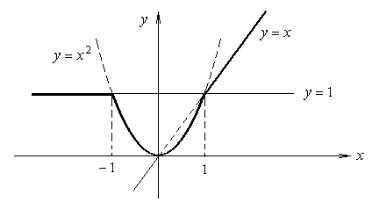
Рис. 1.10.

	1,
		2	,
f (x) = x			,
	x,
	x,

−2 ≤ x ≤ −1,

−1 ≤ x ≤ 1,

1 ≤ x ≤ 2.

		∫	d x = x + C1 ,
		∫

				2			x		8
F (x) = ∫	f (x) d x =	∫ x			d x =					+ C,
F (x) = ∫	f (x) d x =	∫ x			d x =			3		+ C,
								3
		∫ x d x =				x		2		+ C2 ,
						x

							2

−2 ≤ x ≤ −1,

−1 ≤ x ≤ 1,

1 ≤ x ≤ 2.

Постоянные C1 , C, C2 на каждом промежутке должны быть согласованы

с требованием непрерывности первообразной на отрезке интегрирования. Требование непрерывности в точке x = −1 дает

−1+ C =				(−1) 3			+ C, отсюда C =									2		+ C.
−1+ C =							+ C, отсюда C =											+ C.
		1			3									1	3
Из условия непрерывности в точке x = 1 получаем
13		+ C =	12		+ C2 , отсюда C2 = −										1		+ C.
	3	+ C =			+ C2 , отсюда C2 = −												+ C.
	3	2													6
Таким образом, при С = 0					получаем первообразную
					x +					2	,			− 2 ≤ x ≤ −1,
					x +						,			− 2 ≤ x ≤ −1,
							3

		F (x) =				x	3	,						−1 ≤ x ≤ 1,
		F (x) =						,						−1 ≤ x ≤ 1,
					3
					x		2		−		1		,	1 ≤ x ≤ 2.
									−			6	,	1 ≤ x ≤ 2.
					2							6
											30

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.16 Mб3Учебное пособие 1434.pdf
#
30.04.20221.16 Mб16Учебное пособие 1435.pdf
#
30.04.20221.16 Mб4Учебное пособие 1436.pdf
#
30.04.20221.16 Mб114Учебное пособие 1437.pdf
#
30.04.20221.16 Mб2Учебное пособие 1438.pdf
#
30.04.20221.16 Mб15Учебное пособие 1439.pdf
#
30.04.2022300.67 Кб2Учебное пособие 144.pdf
#
30.04.20221.16 Mб4Учебное пособие 1440.pdf
#
30.04.20221.17 Mб4Учебное пособие 1441.pdf
#
30.04.20221.17 Mб1Учебное пособие 1442.pdf
#
30.04.20221.17 Mб7Учебное пособие 1443.pdf