
Учебное пособие 1439
.pdf
Задачи для самостоятельного решения
1. Показать, что если плоскость отсекает на осях координат отрезки, соответственно равные a, b, c , то длина p перпендикуляра, опущенного на эту
плоскость из начала координат, удовлетворяет соотношению
1 + 1 + 1 = 1 . a2 b2 c2 p2
2.В каком отношении плоскость, проходящая через концы трех ребер параллелепипеда, исходящих из одной точки, делит диагональ, исходящую из этой же точки?
3.Вершинами тетраэдра являются точки A(1;2; 3), B(−2;8; 9), C(5; 0;7),
D(3; 4; 2) . Найти радиусы и координаты центров вписанной и описанной
сфер.
4. При каком необходимом и достаточном условии прямая с уравнениями x − x0 = y − y0 = z − z0
l m n
пересекает треугольник с вершинами в точках M k ( xk ; yk ; zk ), k = 1, 2, 3 ?
5.Найти кратчайшее расстояние между диагональю куба и не пересекающей ее диагональю грани, если длина ребра куба равна 1.
6.Найти кратчайшее расстояние между двумя скрещивающимися прямыми, заданными каноническими уравнениями.
7. Даны пять точек A (3; 5;1), B (2; 7; 4), C (1; 0; − 2), D (5; 10;10), E (0; 0; − 5) . Ка-
кие две из данных пяти точек нужно соединить отрезком, чтобы он пересек треугольник, имеющий своими вершинами остальные три точки?
8. При каком необходимом и достаточном условии четыре плоскости Ak x + Bk y + C k z + Dk = 0, k = 1, 2, 3, 4, образуют тетраэдр?
9. Расстояние от точки А до прямой x = y = z равно 
 6 . Найти координаты точки А, если известно, что она лежит на прямой x − y − 3 = 0,
6 . Найти координаты точки А, если известно, что она лежит на прямой x − y − 3 = 0,
2 y + z = 0 .
3.3. Кривые второго порядка
Далее предполагается, что на плоскости введена прямоугольная система координат Оxy, и рассматриваются кривые второго порядка, заданные каноническими уравнениями.
Эллипс имеет каноническое уравнение
x |
2 |
+ |
y |
2 |
= 1, |
(3.3) |
|
a |
2 |
b |
2 |
||||
|
|
|
где а и b – большая и малая полуоси эллипса a ³ b > 0 (рис. 3.12).
111

Точки F1 (c; 0) и F2 (−c; 0) , |
где |
||||
c = |
|
|
|
|
|
a 2 − b 2 |
, называются |
фо- |
|||
кусами эллипса. |
|
||||
Величина |
e = |
c |
называется |
||
|
|||||
|
|
|
a |
|
|
эксцентриситетом эллипса
(0 ≤ e < 1).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояния от |
любой точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M ( x; y) эллипса до фокусов на- |
|||
|
Рис. 3.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зываются ее фокальными ради- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ус-векторами r1 и r2 , при этом |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 = a − e x, |
r2 = a + e x, |
r1 + r2 = 2 a. |
|||||||||
Прямые с уравнениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x = |
a |
, |
|
x = − |
a |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
e |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
||||||||
называются директрисами эллипса, соответственно правой и левой. |
|||||||||||||||||||||||||||
Имеют место равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
r1 |
|
= e |
|
и |
|
r2 |
= e, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
d1 |
|
|
|
|
d 2 |
|
|
|||||||||||||||||
где d 1 и d 2 – расстояния от точки M ( x; y) |
|
эллипса до соответствующей дирек- |
|||||||||||||||||||||||||
трисы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Касательная L к эллипсу в точке M 0 ( x 0 ; y0 ) имеет уравнение |
|||||||||||||||||||||||||||
|
|
|
|
|
x0 x |
|
|
y 0 y |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= 1. |
|
|
|
(3.4) |
||||||||
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
||||||||||||||||
Гипербола имеет каноническое уравнение |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
− |
y 2 |
|
= 1, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a 2 |
b2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где a > 0 – |
действительная полуось, |
b > 0 – мнимая полуось гиперболы. Точки |
|||||||||||||||||||||||||
F (c; 0) и F (−c; 0) , где c = |
|
|
|
, |
|
|
|
||||||||||||||||||||
a2 |
+ b2 |
называются фокусами гиперболы |
|||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 3.13). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямые с уравнениями |
y = |
b |
x и y = − |
b |
x |
являются асимптотами ги- |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|||||||
перболы.
Эксцентриситетом гиперболы называется величина
e = c > 1. a
112

Рис. 3.13.
называются директрисами гиперболы, при этом
Фокальные радиус-
векторы гиперболы вычис-
ляются по формулам
r1 = e x − a, r2 = e x + a
для точек правой ветви и по формулам
r1 = −e x + a, r2 = −e x − a
для точек левой ветви гиперболы, при этом имеет место равенство
r1 − r2 = 2 a.
Прямые с уравнениями
x = |
a |
и |
x = − |
a |
|
e |
|||
|
e |
|
||
|
|
r 1 |
|
= e , |
|
|
r |
2 |
|
|
= e, |
|
|
|
||
|
|
d1 |
|
|
d 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где d 1 – расстояние от точки M ( x; y) |
гиперболы до правой, а d 2 – |
расстояние от |
||||||||||||||
точки M ( x; y) до левой директрисы гиперболы. |
|
|
|
|||||||||||||
Касательная L к гиперболе в точке M 0 ( x 0 ; y0 ) имеет уравнение |
||||||||||||||||
|
x0 x |
− |
y 0 y |
= 1. |
|
(3.5) |
||||||||||
|
|
|
|
|
||||||||||||
|
a2 |
b2 |
||||||||||||||
Парабола имеет каноническое уравнение |
|
|
|
|||||||||||||
|
|
y 2 = 2 p x, |
|
|
|
|
(3.6) |
|||||||||
где p > 0 называется фокальным параметром пара- |
||||||||||||||||
болы (рис. 3.14). |
|
|
|
|
|
|
|
|
|
|
||||||
Точка F |
p |
; 0 |
– фокус параболы. Фокальный |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
||||||
радиус-вектор точки M ( x; y) параболы вычисляется |
||||||||||||||||
по формуле r = x + |
p |
. |
|
|
|
|||||||||||
2 |
|
|
|
|||||||||||||
Рис. 3.14. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для всех точек параболы имеет место равенство r = d или |
r |
= e = 1, где |
||||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d – расстояние от точки M ( x; y) параболы до ее директрисы, |
которая имеет |
|||||||||||||||
уравнение x = − p .
2
113

Касательная L к параболе в |
точке M 0 ( x 0 ; y0 ) |
имеет уравнение |
y |
0 y = p ( x + x 0 ) . |
(3.7) |
Эллипс, гиперболу и параболу можно задать одним уравнением, зависящим от двух параметров, поместив начало прямоугольной системы координат в вершину кривой, как показано на рис. 3.15.
Такое уравнение имеет вид |
|
y 2 = 2 px − (1 − e2 ) x2 , |
(3.8) |
где p − фокальный параметр |
кривой |
второго порядка, равный половине длины хорды, проходящей через фокус перпендикулярно к оси 0x .
|
Для эллипса и гиперболы |
p = |
b 2 |
, а |
|
a |
|||
|
|
|
|
|
|
для параболы параметр p входит в канони- |
|||
|
ческое уравнение. Параметр e – |
эксцентри- |
||
Рис. 3.15. |
ситет. Для эллипса 0 ≤ e < 1 , для параболы |
|||
e = 1 и для гиперболы e > 1. |
|
|
|
|
|
|
|
|
|
Одним уравнением эллипс, гипербола и парабола могут быть заданы также в полярной системе координат , если полюс О поместить в фокус, а полярную ось направить вдоль оси симметрии кривой.
Такое уравнение имеет вид |
|
|
|
r = |
p |
, |
(3.9) |
1 − e cos ϕ |
где p − фокальный параметр, e − эксцентриситет кривой, так же как и в уравне-
нии (3.8)
Упражнение 1. Получить уравнения (2.2), (2.3), (2.5) касательных соответственно к эллипсу, гиперболе, параболе.
Упражнение 2. Найти координаты центра (если кривая центральносимметричная), координаты фокусов кривой второго порядка, заданной уравнением (3.8).
Упражнение 3. Выяснить, какая кривая на плоскости определяется параметрическим заданием:
x = a cos t, |
0 ≤ t < 2π ; |
б) |
|
а) |
x = acht, |
− ∞ < t < +∞ . |
|
y = b sin t, |
|
|
|
|
|
y = bsht, |
|
114

Примеры решения задач
Пример 3.13. Найти отношение площадей вписанного в эллипс квадрата и описанного около эллипса квадрата, если эллипс имеет каноническое уравне-
ние |
x |
2 |
+ |
y |
2 |
= 1, a > b . |
|
a |
2 |
b |
2 |
||||
|
|
|
Решение. Эллипс – кривая, имеющая две оси симметрии. Вписать квадрат в эллипс можно при условии, что две его оси симметрии, проходящие через середины сторон, совпадут с осями симметрии эллипса, а описать можно при условии, что две его оси симметрии, проходящие через диагонали, совпадут с осями симметрии эллипса. (Рекомендуется провести подробное обоснование этих утверждений).
Найдем площадь s вписанного в эллипс квадрата. Из приведенных выше утверждений следует, что вершины вписанного в эллипс квадрата лежат на биссектрисах координатных углов, то есть на прямых с уравнениями y = ± x .
Для вычисления площади |
s |
достаточно знать одну координату любой верши- |
|||||||||
ны квадрата. Подставив y = x |
в уравнение эллипса, получим |
||||||||||
|
x2 |
+ |
x2 |
= 1 x2 |
= |
a2b2 |
. |
|
|
||
|
a2 |
|
|
a2 + b2 |
|||||||
|
|
b2 |
|
|
|
|
|||||
Длина стороны вписанного квадрата равна 2x = 2ab / |
|
. Площадь |
|||||||||
a2 + b2 |
|||||||||||
s = (2x)2 . Таким образом, |
s = |
4a2b2 |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
a2 + b2 |
|
|
|
|
|
||
Найдем площадь S квадрата, описанного около эллипса. Из приведенных в начале решения утверждений следует, что для описанного квадрата вершины лежат на осях координат на одинаковых расстояниях от начала координат. Для вычисления площади S достаточно найти координаты одной вершины описан-
ного квадрата. Пусть это будет точка M1 (x1 ;0) , тогда S = 2x12 . M1 есть точка пересечения касательной к эллипсу в некоторой точке M 0 ( x0 ; y0 ) с осью 0x . Подставим координаты точки M1 в уравнение касательной к эллипсу (2), тогда получим
x x |
0 |
= 1 или x = |
a |
2 |
|
1 |
|
|
. |
||
|
|
|
|
||
a2 |
|
1 |
x0 |
||
|
|
||||
При нахождении координаты x0 учтем, что касательная к эллипсу, яв-
ляющаяся стороной квадрата, лежащей в первой четверти, имеет угловой коэффициент, равный –1. Уравнение (2) касательной в точке M 0 ( x0 , y0 ) с угловым
коэффициентом имеет вид
y = − |
b2 |
|
x0 |
x + |
b2 |
. |
a 2 |
|
|
||||
|
|
y0 |
|
y0 |
||
115 |
|
|
|
|||


Отсюда получаем условие касания прямой y = kx + l эллипса |
x2 |
+ |
y2 |
= 1: |
|
a2 |
b2 |
||||
|
|
|
|||
a 2 k 2 + b 2 − l 2 = 0 . |
|
|
|
||
В нашей задаче это условие имеет вид |
|
|
|
||
a2 k 2 + b2 = (Y − kX )2 , |
|
|
|
||
то есть угловой коэффициент k должен быть решением квадратного уравнения
(a2 − X 2 )k 2 + 2X Y k + (b2 − Y 2 ) = 0 .
Условие перпендикулярности касательных, заданных уравнениями с угловым коэффициентом, есть ki k 2 = −1 . Применяя теорему Виета, получаем ус-
ловие перпендикулярности в нашем случае
b2 − Y 2 = −1. a2 − X 2
Это и есть уравнение искомого геометрического места точек, которое можно записать в виде
X 2 + Y 2 = a 2 + b 2 .
Последнее уравнение есть уравнение окружности с центром в начале ко-
ординат и с радиусом R = 
 a 2 + b2 .
a 2 + b2 .
Замечание. Результат решения этой задачи можно использовать для вычисления площади квадрата, описанного около эллипса. Рекомендуем рассмотреть этот подход к решению второй части примера 3.13.
Пример 3.15. Составить уравнение геометрического места точек, симметричных центру эллипса относительно касательных к этому эллипсу.
Решение. Точка (x; y) |
искомого геометрического места, соответствующая |
|||||||||||
касательной |
x0 |
x + |
y0 |
y = 1 |
к эллипсу |
x2 |
+ |
y2 |
= 1 |
в точке |
( x0 , y0 ) , лежит на |
|
|
|
|||||||||||
a 2 |
b2 |
a2 |
b2 |
|||||||||
|
|
|
|
|
|
|
|
|||||
перпендикуляре к этой касательной, проходящем через начало координат. Уравнение этого перпендикуляра имеет вид
|
x − 0 |
= |
|
y − 0 |
|
или y = |
a2 |
|
y0 |
x . |
|||||||||||||||
|
x0 / a2 |
y0 / b2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
b2 x0 |
|||||||||||||||||||
Решая совместно уравнение касательной и перпендикуляра к ней, нахо- |
|||||||||||||||||||||||||
дим координаты точки пересечения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
y0 |
|||||||||
|
|
|
|
x0 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x = |
|
|
|
y = |
|
b2 |
|||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
. |
|||||||||||||
x02 |
|
a2 y02 |
x02 |
+ |
a2 |
|
y02 |
|
|||||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
a 2 |
b2 |
|
b2 |
|
|
||||||||
|
|
a2 |
b2 |
b2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
117 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Координаты ( X ,Y ) точки искомого геометрического места находим из формул деления отрезка пополам
X + 0 |
= x , |
Y + 0 |
= y , |
|
2 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
2 |
y0 |
|||||
|
2x0 |
|
|
|
|
|
|
|
|||||||||
X = |
|
|
|
Y = |
|
b |
2 |
||||||||||
|
|
, |
|
|
|
|
|
|
|
. |
|||||||
x02 |
+ |
a2 |
|
y02 |
|
x02 |
+ |
a 2 |
|
y02 |
|
||||||
|
|
|
|
|
|
|
|
a2 |
b2 |
|
b2 |
||||||
|
a 2 |
b2 |
|
b2 |
|
|
|||||||||||
Для получения уравнения, связывающего X иY , нужно исключить из последних равенств x0 и y0 . Возводя в квадрат левую и правые части этих ра-
венств и складывая их, получаем
|
|
|
|
|
|
x2 |
+ |
a 2 |
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
b2 |
|
|
|
|
|
4a 2 |
|
|
|
|
|||||||||||
X |
2 |
+ Y |
2 |
= 4 |
|
|
0 |
|
|
|
|
0 |
|
|
= |
|
|
|
|
|
. |
||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
x02 |
+ |
a 2 |
|
y02 |
||||||
|
|
|
|
|
|
x0 |
|
+ |
a |
|
|
|
y0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a 2 |
b2 |
|
b2 |
||||||||||||||
|
|
|
|
|
|
|
2 |
|
b |
2 |
|
b |
2 |
|
|
|
|
||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Умножая первое равенство на a , второе на b , возводя в квадрат и складывая, получим
|
|
|
|
|
|
|
|
|
4a |
2 x |
2 |
+ |
4a 4 y02 |
|
|
4a 2 x |
2 |
+ |
a 2 |
|
y 2 |
|
|
|
4a 4 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
a |
2 |
x |
2 |
+ b |
2 |
y |
2 |
= |
|
|
|
|
0 |
|
|
|
|
b2 |
|
|
= |
|
|
|
|
0 |
|
|
0 |
= |
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
2 |
|
|
a |
2 |
|
|
2 |
|
2 |
|
|
2 |
|
|
a |
2 |
|
|
|
2 |
|
2 |
|
2 |
|
a |
2 |
|
|
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
x0 |
+ |
|
|
|
y0 |
|
|
x0 |
+ |
|
|
|
y0 |
x0 |
+ |
|
|
y0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
b |
2 |
|
b |
2 |
|
|
|
|
|
|
2 |
b |
2 |
|
|
b |
2 |
|
|
|
|
2 |
b |
2 |
|
b |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||
Сравнивая это равенство с предыдущим, получаем искомое уравнение
( X 2 + Y 2 )2 = 4(a2 x2 + b2 y 2 ) .
Замечание. Задача из этого примера может быть поставлена в одной из следующих механических интерпретациях.
А. Эллипс катится без проскальзывания по равному ему эллипсу, причем вначале большие оси обеих линий расположены на одной прямой (рис. 3.16). Найти геометрическое место, которое описывает центр подвижного эллипса.
Б. Две одинаковые шестеренки, имеющие форму эллипса, закреплены шарнирно каждая в одном из фокусов,
как показано на рис. 3.16. Расстояние между закрепленными фокусами равно
длине большой оси |
F1F1' |
= 2a . |
Рис. 3.16. |
|
|
|
118 |

Докажите, что эти шестерни могут вращаться, все время соприкасаясь в одной точке, образуя эллиптическую передачу.
Пример 3.16. Гипербола задана каноническим уравнением |
x |
2 |
− |
y |
2 |
= 1. |
a |
2 |
b |
|
|||
|
|
|
|
Доказать справедливость следующих утверждений:
а) произведение отрезков, отсекаемых касательной на ее асимптотах (считая от центра), есть величина постоянная. Найти эту постоянную;
б) площадь треугольника, образованная асимптотами гиперболы и произвольной касательной, постоянна. Найти эту площадь;
в) отрезок любой касательной гиперболы, заключенный между асимптотами, делится точкой касания пополам;
г) площадь параллелограмма, одна из вершин которого лежит на гиперболе, а две стороны – на асимптотах, постоянна. Найти эту площадь.
Решение
А. Найдем точки пересечения асимптот гиперболы с касательной к ней в точке ( x0 ; y0 )
|
= ± |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
x , |
|
x0 x y0 |
|
b |
|
|
a |
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
± |
|
|
|
|
x = 1, x1,2 |
= |
|
|
|
, y1,2 |
= ± |
|
|
|
= |
|
|
|
|
. |
||
|
|
|
|
|
|
a |
2 |
b |
2 |
|
x0 |
|
y0 |
x0 |
|
|
|
y0 |
|
|
||||||||||||
x0 x |
+ |
|
y0 y |
= 1, |
|
|
|
|
a |
|
± |
|
|
± |
y0 |
|
|
|
± |
x0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
a |
b |
b |
a |
||||||||||
|
2 |
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Найдем расстояния d1 , d 2 от начала координат до точек пересечения касательной с асимптотами:
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
a2 + b2 |
|
|
= |
|
|
|
|
c |
. |
|
||||||||||||||||||||||||
|
d |
|
x2 |
+ y2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|||||||||||||||||||||||||
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 ± y0 2 |
|
|
|
|
± |
y0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|||||||||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d d |
|
= |
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
c2 |
|
|
|
|
|
= c2 . |
|||||||||||
|
|
x |
|
|
|
y |
|
|
x |
|
|
y |
|
|
|
|
x2 |
|
|
|
y2 |
|
||||||||||||||||||||||||||
|
1 |
2 |
|
|
|
+ |
|
0 |
|
− |
|
0 |
|
|
|
|
|
− |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
b a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Б. Площадь S искомого треугольника равна |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
S = |
1 |
d d |
|
sinα = |
1 |
c2 sinα , |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где α − угол между асимптотами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
α |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
2tg α |
|
|
|
|
|
|
|
|
b |
|
|
|
1 |
|
|
|
|
|
|
|
ab |
||||||||||
tg |
2 = |
|
, sinα = |
2 |
= 2 |
|
|
|
|
|
|
= 2 |
|
. |
||||||||||||||||||||||||||||||||||
a |
1 + tg2 α |
a |
1 + |
b2 |
|
c2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
||||
Отсюда площадь S = 1 c2 2 ab2 = ab.
2 c
В. В пункте а были найдены координаты точек пересечения касательной с асимптотами. Найдем суммы одноименных координат.
119
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
− |
|
y |
0 |
+ |
x |
0 |
+ |
y |
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x + x |
2 |
= |
|
|
a |
|
|
+ |
|
|
a |
|
= |
|
a |
|
|
|
b |
|
|
a |
b |
= 2x |
0 |
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
x0 |
+ |
y0 |
|
|
|
x0 |
− |
y0 |
|
|
|
|
|
|
|
|
|
x02 |
|
− |
y02 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
a |
b |
a |
b |
|
|
|
|
|
a |
2 |
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда |
x0 = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y1 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично получаем, что y0 |
= |
. Это формулы деления отрезка с |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
концами в точках (x1; y1 ) , (x2 ; y2 ) пополам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
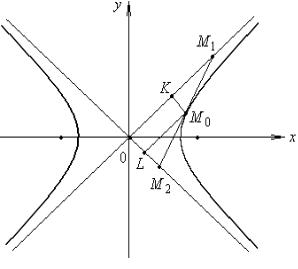
Г. Пусть M 0 – |
вершина параллелограмма, лежащая на гиперболе. Прове- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дем через нее касательную к гиперболе |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до пересечения с асимптотами. Стороны |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольника, выходящие из вершины |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 |
согласно пункту б, являются сред- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ними линиями |
|
|
в треугольнике OM 1M 2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис.3.17), поэтому площадь параллело- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грамма OKM 0 L равна половине площа- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ди треугольника OM 1M 2 , вычисленной в |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пункте б. Отсюда для любой точки M 0 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболы Sпар. |
= |
1 |
ab . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
Рис. 3.17.
Пример 3.17. Доказать, что середины хорд параболы, параллельных касательной к параболе в точке M 0 , лежат на прямой, параллельной оси параболы
и проходящей через точку M 0 .
Решение. Пусть уравнение параболы y 2 = 2 px , тогда уравнение касательной к ней в точке M 0 ( x0 ; y0 ) имеет вид y0 y = p ( x + x0 ) . Хорда, параллельная касательной и проходящая через точки M1 (x1; y1 ) и M 2 (x2 ; y2 ) параболы, имеет тот же угловой коэффициент, то есть
|
|
|
y2 − y1 |
= |
|
p |
или |
y |
2 |
− y = |
|
p |
(x |
2 |
− x ) . |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
x2 − x1 |
|
|
y0 |
|
|
|
1 |
|
y0 |
|
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Из уравнения параболы выражаем x1 и x2 |
через y1 |
и y2 . |
||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
y 2 |
|
y 2 |
|
|
1 |
|
|
|
|
|
|
|
|
||
y |
2 |
− y = |
|
|
|
|
2 |
− |
1 |
= |
|
( y |
2 |
− y )( y |
2 |
+ y ) . |
||||||
|
|
|
|
|
||||||||||||||||||
|
1 |
y0 |
|
|
|
|
|
|
|
|
2 y0 |
1 |
|
1 |
||||||||
|
|
|
|
|
|
2 p 2 p |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
