Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1439

.pdf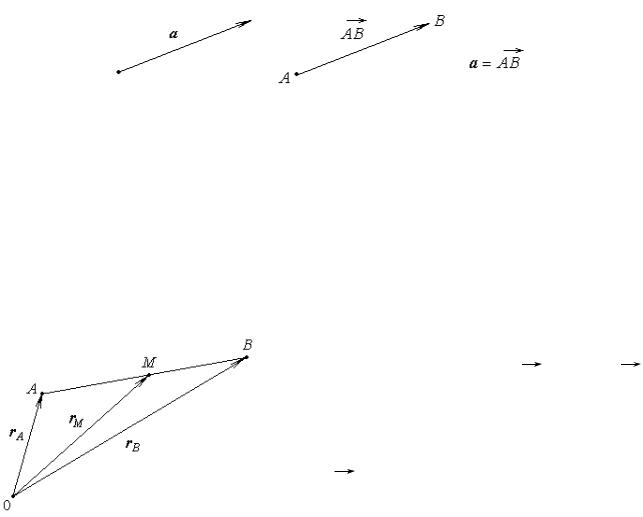

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.16 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1310 11 12 13 > Следующая >>>

3.ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

3.1.Векторы в геометрических задачах

Вэтом разделе под термином вектор понимается геометрический вектор, который можно представлять себе как направленный отрезок, начало которого может быть помещено в любой точке пространства. Обозначается вектор либо одной строчной буквой жирным шрифтом, либо двумя заглавными, со стрелкой над ними (рис. 3.1.)

Рис. 3.1.

Разложение вектора a в ортонормированном базисе (i, j, k) записывается в виде

a = a1 i + a 2 j + a 3 k.

Далее приводятся некоторые соотношения векторной алгебры, часто применяемые при решении геометрических задач.

Формула деления отрезка в данном отношении

Пусть О –

произвольно выбранная точка

пространства.

Векторы

rA = ОА ,

rB = ОВ

называются радиус-векторами соответственно

точек А, В (рис. 3.2.)

Радиус-вектор

точки

М,

делящей

вектор АВ, в отношении λ =

АМ

М В

Рис. 3.2.

rA + λ rB

определяется формулой

. Это соотношение может быть запи-

1+ λ

0 ≤ α ≤ 1,

α =

сано также в виде rM = α r A + (1 − α) rB ,

+ λ

rA + rB

В частности, при делении отрезка АВ пополам λ = 1 и

Скалярное произведение двух векторов определяется формулой

(a,b) = a b cos (a,b) .

Некоторые свойства скалярного произведения

1. Связь с проекцией:

(a,b) = a Прab = b Прba,

где Прba означает числовую проекцию вектора a на вектор b . 2. Условие ортогональности векторов:

a b (a, b) = 0.

Выражение скалярного произведения в прямоугольной системе коорди-

нат:

(a, b) = a1 b1 + a 2 b 2 + a 3 b3 ,

a = (a, a) = 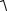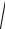a12 + a 22 + a 23 .

Векторное произведение двух векторов a и b есть вектор c = [a,b], оп-

ределяемый условиями

а) c = [a,b] = a b sin (a ,b) ;

б) c a и c b ;

в) a, b, c – правая тройка векторов .

Основные свойства векторного произведения

1) [b,a] = −[a,b];

2) условие коллинеарности векторов: a b b = λ a [a, b] = 0 ; 3) площадь параллелограмма: S = [a, b]

Рис. 3.3.

Выражение векторного произведения в прямоугольной системе коорди-

нат:

	i	j	k
[a, b] =	a1	a 2	a 3	= (a 2b3 − a 3b2 ) i − (a1b3 − a 3b1 ) j + (a1b2 − a 2b1 ) k .
	b1	b2	b3

Смешанное произведение трех векторов a, b, c определяется равенством

(a,b,c) = ([a,b],c) .

Основные свойства смешанного произведения

1)(a, b, c) = (b, c, a) = (c, a, b) ;

2)условие компланарности трех векторов

c = α a

V , 3) (a,b,c) =

−V ,

+ βb (a, b, c) = 0;

если a,b,c − правая тройка; если a,b,c − левая тройка,

где V – объем параллелепипеда, построенного на векторах a, b, c, как на сторонах (рис. 3.4).

Выражение смешанного произведения в прямоугольной системе координат:

	(a, b, c) =	a1	a	2	a 3
Рис. 3.4.	(a, b, c) =	b1	b	2	b3
		c1	c	2	c3

Упражнение 1. Доказать, что объем тетраэдра, построенного на векторах

a, b, c, равен 1 (a, b, c) .

Двойное векторное произведение трех векторов a, b, c:

[a,[b,c] ]= a×(b×c) .

При решении задач, использующих различные произведения векторов, полезными являются следующие тождества:

[a,[b,c] ]= b(a,c) −c(a,b) ,

(a,b)2 +

[a,b]

2 =

2 или [a, b]2 =

(a, a)

(a, b)

(b, a)

(b, b)

([a, b],[c, d ] ) =

(a, c)

(a, d )

(b, c)

(b, d )

(a, a) (a, b) (a, c) (a, b, c)2 = (b, a) (b, b) (b, c) .

(c, a) (c, b) (c, c)

Эти соотношения позволяют все вычисления с различными произведениями векторов сводить к вычислениям лишь скалярных произведений.

Упражнение 2. Доказать приведенные тождества.

Отметим, что многие задачи геометрии, связанные с внутренними свойствами фигур, а не с их расположением в пространстве, могут быть решены в векторном виде без привлечения метода координат (здесь имеется в виду введение прямоугольной системы координат).

Примеры решения задач

Пример 3.1. Докажите, что для любого конечного набора точек A1 , A2 ,... An (на плоскости или в пространстве) найдется единственная точка М

такая, что выполняется равенство
M A1 + M A2 + ... + M An = O .	(3.1)
Решение. Выберем произвольную точку О в качестве полюса и проведем
из нее радиус-векторы ОМ и OA k ,	k = 1, 2,..., n .

Тогда для точки Ak имеем MA k = OA k − OM и MA1 + MA 2 + ... + MA n =

= (OA1 - OM ) + (ОА2 - OM ) + ... + (OA n - OM ) =

	= (OA1 + OA 2 + ... + OA n ) − n OM = 0 .
	Отсюда следует, что равенство (3.1) выполняется то-
	гда и только тогда, когда
	uuuur	1 uuur		uuur	uuur
Рис. 3.5.	OM =		(OA1	+ OA2	+ ... + OAn).	(3.2)

		n

Равенство (3.2) определяет вектор ОМ , а значит, и искомую точку М

(рис. 3.5).

Замечание. Точка М, определяемая равенством (3.1), называется цен- троидом системы n точек A1 , A2 ,... An . (Эта точка является центром единичных

масс, помещенных в точках A1 , A2 ,... An ).

Пример 3.2. Укажите положение центроида для треугольника. Решение. Для треугольника АВС равенство (3.2) принимает вид

uuuur		1	uuur uuur uuur
OM	=		(OA + OB + OC).
OM	=	3	(OA + OB + OC).
		3

Выберем в качестве полюса точку А – вершину треугольника. Тогда

	uuuur	1 uuur uuur		2		AB + AC		2	uuur
	AM =		( AB + AC) =		×		=		× A A ,

		3		3		2		3	1
	где A1 − середина стороны ВС треугольника. Отсюда сле-
	дует, что точка М лежит на медиане A A1 и делит ее в от-
	ношении 2:1 (рис. 3.6). Если в качестве полюса вместо А
	взять другие вершины В или С треугольника, то получим
	аналогичный результат. Это означает, что точка М являет-
Рис. 3.6.	ся общей для трех медиан треугольника и делит все их в
	отношении 2:1, считая от соответствующей вершины тре-
	угольника. Таким образом, получена известная теорема
элементарной геометрии.
Пример 3.3. В треугольнике АВС на сторонах АВ, ВС ,								САвыбраны со-
			uuur			uuur		CB' = γ CA . При
ответственно точки C ', A', B' так, что AC' =α AB,				BA '= β BC,

каком необходимом и достаточном условии векторы AA', BB ' и CC ' образуют

треугольник.

Решение. Из векторов можно образовать треугольник, если их сумма равна нулю, то есть AA' + BB '+ CC '= О .

Обозначим AB = a, AC = b . Тогда BC = b − a ,

AA' = a + β (b − a) ,

BB' = b − a − γ b , CC' = −b + α a .

Рис. 3.7.	'+ CC	'=
AA' + BB

=a + β(b − a) + b − a − γ b − b + α a =

=(α − β) a + (β − γ) b = 0 (рис. 3.7)

Так как векторы a и b не коллинеарны, то равенство возможно тогда и только тогда, когда α − β = 0 и β − γ = 0, то есть когда α = β = γ .

Пример 3.4. Точки C ', B', A' делят стороны АВ, ВС, СА треугольника АВС в одинаковом отношении:

BA'

= α .

Определить, при каком значении α:

а) площадь S (α) треугольника, образованного векторами AA', BB ' и CC ' , наименьшая;

б) площадь S '

' ' (α)

треугольника A'B'C '

наименьшая;

A B C

Решение:

uuur uuur

а) S (α ) =

. Выражения для векторов

AA ,С С

C C возьмем

из примера 3.3, положив β = α. Тогда

S (α ) =

[ (1− α ) a + α b, b − α a ]

(1−α )[a, b] − α 2[b, a]

= (1−α + α 2 )

[a, b]

= (1− α + α 2 )SABC .

S '(α ) = (−1+ 2α 2 )SABC = 0

α =

Отсюда следует, что S (α) достигает минимума при α =

, то есть когда

AA', BB' и CC '– медианы треугольника АВС. При этом S

S ABC ;

uuuur

б) S

(α ) =

' '

A B , A C

Найдем выражения векторов A B

A C

A B C

через векторы a и b , пользуясь данными примера 3.3 при условии β = γ = α.

A B

A A + AB = (α −1)a − α b + (1 − α )b = (α −1)a + (1 − 2α )b ,

α a = (2α −1)a −α b.

A C

= A A + AC

= (α −1)a − α b +

' ' ' (α) =

[ (α −1) a + (1 − 2 α) b, (2 α − 1) a − α b]

A B C

α (1 − α) [a, b] + (1 − 2 α)2 [a, b]

= (α − α 2 + 1 − 4 α + 4 α 2 )

[a, b]

= (1 − 3α + 3α2 ) S

ABC

' ' ' (α ) = (−3

+ 6α ) SABC = 0

α =

' ' '

S ABC .

A B C

A B C 2

Пример 3.5. На сторонах АВ, ВС и СА треугольника АВС, площадь кото-

рого равна

взяты

соответственно

точки

C ', A', B '

так,

что

AC' = λ C 'B ,

BA' = λ2 A'C ,

CB' = λ3 B'A и

прямые

AA', BB' и CC '

попарно

пересекаются.

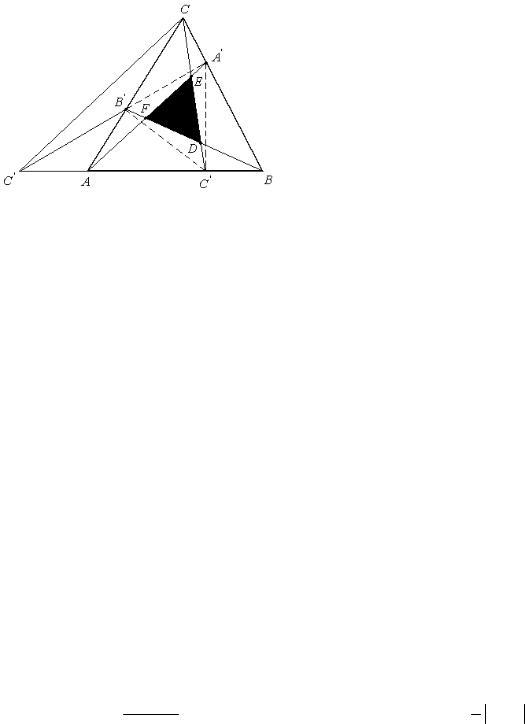
Найти: а) площадь треугольника A'B 'C ', б) площадь треугольника, полученного при пересечении прямых AA', BB' и CC ' (рис. 3.8).

Решение:

	' ' '=	1	uuuur	uuuur	'

а) S			' '	'		.
			A B , A C
		2
	A B C

Обозначим AB = a, AC = b. ТогдаBC = b − a,

'	'	'	'
A B		= A C + CB ,
'	'	'	'	Из соотношений
A C		= A B + BC .		Из соотношений

Рис. 3.8

uuur

BA' + A'C = BC

uuur

= b − a

λ2 A C

+ A C

= BC

A C

Аналогично

uuur

= −λ3b

uuur

= λ3 B A = λ3(CA − CB )

− λ3CB

Отсюда

uuuur

λ3

A B

(b − a) −

b = −

a +

1+ λ

uuur

A B = λ2 CA =

λ2 (CB − A B)

= λ2 (a − b) − λ2 A B

uuuur

uuur

uuuur

C A

(BA − BC )

= −

−

'	'	получаем
и BA	= λ2 A C	получаем

(b − a).

1+ λ

λ3

uuur

CB = −

1 + λ

1− λ2λ3

b ;

(1+ λ2) (1+ λ3)

uuur

λ2

− b);

A B

1 + λ

uuuur

BC = −

1+ λ

uuuur

λ2

λ1λ2 −1

λ2

' '

A C

(a − b) −

a =

a −

1+ λ

(1+ λ ) (1+ λ )

1+ λ

S ' ' '=

uuuur

[a,b] +

(1 − λ λ ) (λ λ −1)

[b,a]

[ A B , A C ]

(1 + λ )2

(1 +

λ ) (1

+ λ

(1 + λ

A B C

)

=1 λ2 (1+ λ1 ) (1+ λ3 ) + (1− λ1 λ2 − λ2 λ3 − λ1 λ22 λ3 ) 1 [a,b] =

+λ2 )2 (1+ λ1 ) (1+ λ3 ) 2(1

=	λ1 λ2 λ	3	+1	S.
=	+ λ1 ) (1+ λ			S.
(1	+ λ1 ) (1+ λ	2 ) (1+ λ3 )
	97

Это и есть искомая площадь треугольника DEF.

Замечание. Используя результат решения этой задачи, можно получить утверждение, известное как теорема Менелая.

Пусть на сторонах (ВС), (СА), (АВ) (или их продолжениях) треугольника АВС взяты соответственно точки A', B',C '. Точки A', B', C ' лежат на одной прямой тогда и только тогда, когда

AC ' BA' CB ' = −

C 'B A'C B'A

Упражнение 2. Доказать теорему Менелая, используя результаты примера 3.5. Найти другие доказательства этой теоремы.

Найти площадь треугольника DEF (см. рис. 2.8).

uuur

SDEF

[ FE, FD ]

FE = AE − AF,

FD = FB − DB.

uuur

= α1 AA ,

= α2 AA .

uuur

BD = β1BB ,

= β2 BB .

uuur

= γ1CC ,

= γ 2CC .

uuur

uuur uuur

λ2

a + λ2b

AA' = AB + BA '= a +

(b − a) =

+ λ

1+ λ

uuur

uuuur

uuur

uuuur

λ1

= BA + AB

= −a +

= CA + AC

a − b.

1+ λ

Для нахождения чисел α1 , α 2 , β1 , β2 , γ1 , γ 2 применим часто используемый прием: «правило цикла». Рассмотрим треугольник (цикл) AFB.


AF + FB = AB			α1 AA1 − β2 BB1 = AB
	a + λ 2 b		1
α1		− β2			b + β2 a = a
α1	1 + λ 2	− β2		1 + λ3	b + β2 a = a

α1

+ β 2

= 1,

α1 =

1 + λ 2

1 + λ

2 + λ 2 λ 3

λ 2

(1 + λ 3 )

α1

− β 2

1 + λ 2

1 + λ3

1 + λ 2 + λ 2 λ 3

Аналогично из циклов АЕС и BDC находим соответственно

λ1 (1 + λ 2 )

β1

1 + λ 3

+ λ1

+ λ1 λ 2

+ λ

3 + λ1 λ 3

1 + λ1

λ 3

(1 + λ1 )

1 + λ 1 + λ1 λ 2

1 + λ 3 + λ 1 λ 3

Заметим, что коэффициенты β1, γ1 можно получить из α1 , а α1 и γ1 – из

β 2 круговой перестановкой индексов.

Теперь для FE и FD получаем выражения

uuur

(1 + λ2 )(λ1λ2λ3 −1)

a + λ2b

FE = (α2 − α1) AA'=

;

+ λ1

+ λ1λ2 )(1 + λ2 + λ2λ3) (1 + λ2 )

uuur

(1 + λ3)(1 − λ1λ2λ3)

b − (1 + λ3)a

FD = (β1

− β2 )BB '=

;

(1 + λ2 +

λ2λ3)(1 + λ3 +

λ1λ3)

1 + λ3

uuur

FE, FD

DEF

(λ λ λ −1)2

[a + λ2b,(1 + λ3 )a − b]

2 (1+ λ + λ λ )(1+ λ + λ λ )2 (1+ λ + λ λ )

(λ λ λ −1)2

λ2 + λ2λ3 )

[b, a]

= (1+ λ + λ λ )(1+ λ + λ λ )2 (1+ λ + λ λ ) (1+

(λ λ λ −1)2

(1+ λ1 + λ1λ2 )(1+ λ2 + λ2λ3 )(1+ λ3 + λ1λ3 )

Это и есть искомая площадь треугольника DEF.

Замечание. Из результата решения этой задачи можно получить утверждение, известное в геометрии как теорема Чевы.

Пусть на сторонах (ВС), (СА), (АВ) треугольника АВС взяты соответ- ственно точки A', B',C' . Прямые (AA'), (BB'), (CC') пересекаются в одной точке тогда и только тогда, когда

AC' BA' CB' =

1 .

C'B A'C B' A

Упражнение 3. Получить утверждение теоремы Чевы, используя результат примера 3.5. Найти другие доказательства этой теоремы.

Теорема Чевы замечательна тем, что следствиями из нее являются известные теоремы геометрии. Их предлагается доказать в следующем упражнении.

Упражнение 4. Применяя теорему Чевы, докажите, что а) медианы треугольника пересекаются в одной точке;

б) биссектрисы треугольника пересекаются в одной точке; в) высоты остроугольного треугольника пересекаются в одной точке;

г) прямые, соединяющие точки касания вписанной в треугольник окружности с противоположными вершинами, пересекаются в одной точке.

Пример 3.6. На каждой из четырех граней тетраэдра OABC взята точка и из нее проведен единичный вектор, перпендикулярный к этой грани и лежащий вне тетраэдра. Пусть s1 , s2 , s3 , s4 , – площади граней, a n1 , n2 n3 , n4 – единичные векторы, соответственно перпендикулярные к этим граням. Показать, что

s1n1 + s2 n2 + s3n3 + s4 n4 = 0 .

Решение. Обозначим OA = a, OB = b, OC = c, площадь треугольника OAB

через s1,		OBC через s2 ,												OCA через s3 ,							ABC через s4 .
Тогда
uuur						uuur												1	[a,b], s2n2 =			1	[b,c], s3n3		1	[c,a],
AC		= c − a, AB								= b − a, s1n1 =								1				1		=	1
AC		= c − a, AB								= b − a, s1n1 =														=
																	2				2			2
						s4n4 =					1		[c − a, b − a] =							1	[c, b]− [c, a]− [a, b] .
						s4n4 =							[c − a, b − a] =								[c, b]− [c, a]− [a, b] .
											2						2
Отсюда
s n + s				n		+ s		n		+ s		n			=	1	( [a, b]+ [b, c]+ [c, a]+ [c, b]− [c, a]− [a, b] ) = 0 .
s n + s			2	n	2	+ s	3	n	3	+ s	4	n		4	=		( [a, b]+ [b, c]+ [c, a]+ [c, b]− [c, a]− [a, b] ) = 0 .
1	1		2		2		3		3		4			4	2
															2

Упражнение 5. Обобщить доказанное утверждение на случай любого выпуклого многогранника.

Пример 3.7. Определить угол А треугольника между сторонами равными 2 и 4, если биссектриса угла А равна 43 .

Решение. Пусть AB = 2 , AC = 4 , AD − биссектриса, a = AB , b = AC .

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1310 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.16 Mб3Учебное пособие 1434.pdf
#
30.04.20221.16 Mб16Учебное пособие 1435.pdf
#
30.04.20221.16 Mб4Учебное пособие 1436.pdf
#
30.04.20221.16 Mб114Учебное пособие 1437.pdf
#
30.04.20221.16 Mб2Учебное пособие 1438.pdf
#
30.04.20221.16 Mб15Учебное пособие 1439.pdf
#
30.04.2022300.67 Кб2Учебное пособие 144.pdf
#
30.04.20221.16 Mб4Учебное пособие 1440.pdf
#
30.04.20221.17 Mб4Учебное пособие 1441.pdf
#
30.04.20221.17 Mб1Учебное пособие 1442.pdf
#
30.04.20221.17 Mб7Учебное пособие 1443.pdf