Модели и алгоритмы проектирования и разработки систем поддержки принятия инвестиционных решений. Морозов В.П., Баркалов С.А

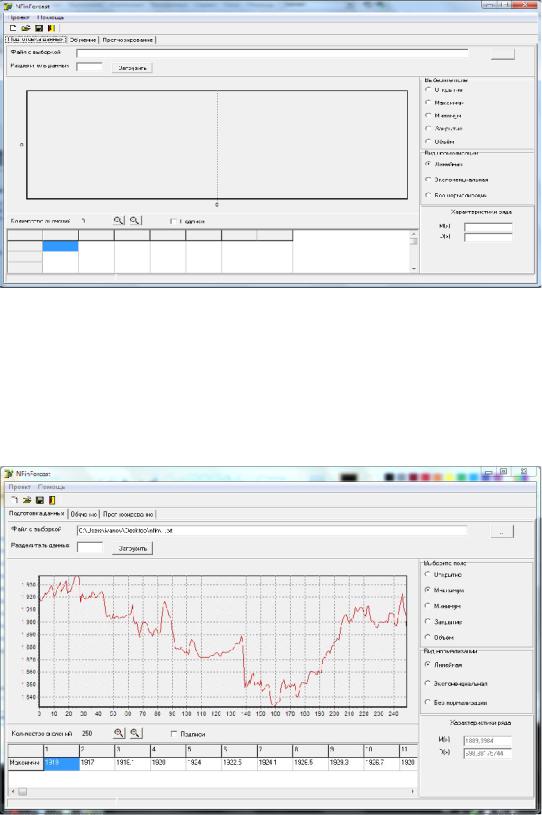
Рис. 2.42. Главная экранная форма ПК НПВР

способ их нормализации. В данной версии ПК НПВР предусмотрена линейная и экспоненциальная нормализация, а также ее отсутствие. На рис. 2.43 представлен пример визуального отображения загруженной обучающей выборки с вычисленными значениями ее статистических характеристик – математического ожидания и дисперсии.

Рис. 2.43. Экранная форма ПК НПВР с загруженной обучающей выборкой

Вкладка «Обучение» реализует структурную настройкуИНС (рис. 2.44).

141

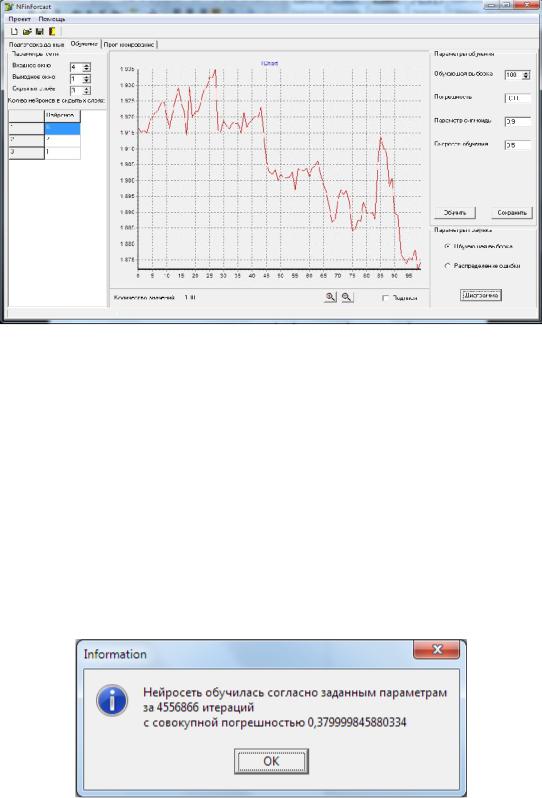
Рис. 2.44. Экранная форма ПК НПВР с открытой вкладкой «Обучение»

Она позволяет задать параметры обучения, в том числе: размер обучающей выборки, уровень погрешности, параметр сигмоиды, скорость обучения. В левой верхней части данной экранной формы расположена панель «Параметры сети», внутри которой можно задавать необходимую конфигурацию ИНС. Панель «Параметры графика», которая размещена в нижней правой части экранной фомы, предоставляет возможность просмотра графика обучающей выборки и распределения ошибки после обучения. Кнопка «Обучить» запускает модуль «Алгоритм обратного распространения ошибок», внутри которого инициируется введённая конфигурация сети и параметры обучения. После этого происходит обучение сети. Результаты обучения ИНС (количество итераций и достигнутая погрешность) отображаются в окне информации - «Information» (рис. 2.45).

Рис. 2.45. Внешний вид окна «Information»

Чтобы сохранить обученную сеть, необходимо нажать кнопку «Сохранить». При этом появится типизированное окно сохранения файла Windows, где

142

следует указать место сохранения файла и нажать кнопку «Сохранить». Нейронная сеть будет сохранена в текстовый файл с расширением .txt.

Для дальнейшей работы с ПК НПРВ – прогнозирования наобходимо перейти на вкладку «Прогнозирование» (рис. 2.46).

Рис. 2.46. Экранная форма ПК НПВР с открытой вкладкой «Прогнозирование»

На панели «Параметры прогнозирования» данной вкладки необходимо выбрать вид прогноза. Одношаговый прогноз является результатом единичного прогнозирования. При многошаговом прогнозе многократно реализуется последовательное применение прогноза и обучения. После этого задаётся количество предсказаний и нажимается кнопка «Прогноз». Пример экранной формы с результатами прогноза приведен на рис. 2.47. Нажатие кнопки «Сохранить»

Рис. 2.47. Экранная форма ПК НПВР с результатами прогноза

143

позволяет записать полученные результаты прогноза в текстовый файл. Нажатие кнопки «Загрузить сеть» позволяет загрузить ранее обученную ИНС из файла и использовать ее для прогнозирования.

Для апробации работоспособности ПК НПВР была проведена серия экспериментов по прогнозированию курса акций Сбербанка РФ.

Обучение сети проводилось на 10–минутном, часовом и суточном интервале представления данных. Для каждого из вариантов формировалась выборка изменения курса акций за один и тот же период – с 15.04.14 по 01.05.14.

Каждый эксперимент разбивался на этапы.

Первым этапом было формирование обучающей выборки. На данном этапе определялся вид представления исторических и прогнозируемых данных и формировался набор входных и выходных сигналов. На втором этапе выбиралась архитектура сети и проводилась настройка параметров обучения. Третьим этапом являлось обучение нейронной сети на основе сформированной на первом этапе обучающей выборки. Обучение останавливалось в случае, если ошибка обучения не превышала значения 0,01. На завершающем этапе осуществлялось тестирование ИНС и определялось качество прогноза котировок и других экономических показателей, позволяющих судить о состоятельности и применимости нейронной сети в данной конфигурации.

Всего было проведено 23 эксперимента. Рассматривались 10-минутный, часовой и суточный графики котировок. В результате выяснилось, что качество прогноза зависит от протяженности интервала представления входных данных. Чем больше интервал, тем выше качество прогноза. Это объясняется тем, что на большем интервале меньше так называемого «шума», т.е. случайных колебаний, мешающих качественному обучениюсети.

В 11 из проведенных экспериментов получен положительный результат прогнозирования. Первые 12 экспериментов показали результат со значительными погрешностями. Начиная с 13 эксперимента, ошибка сети уменьшилась до приемлемых значений (в среднем до 1,8 %). Это было достигнуто за счет оптимизации структуры нейросети.

На рис. 2.48-2.50 представлены результаты прогнозов трех показательных экспериментов. Параметры экспериментов приведены в табл. 2.14.

Таблица 2.14

Параметры экспериментов исследования ИНС

Во всех экспериментах, в качестве критерия отбора входных данных используется поле «Объем» и линейная нормализация.

144

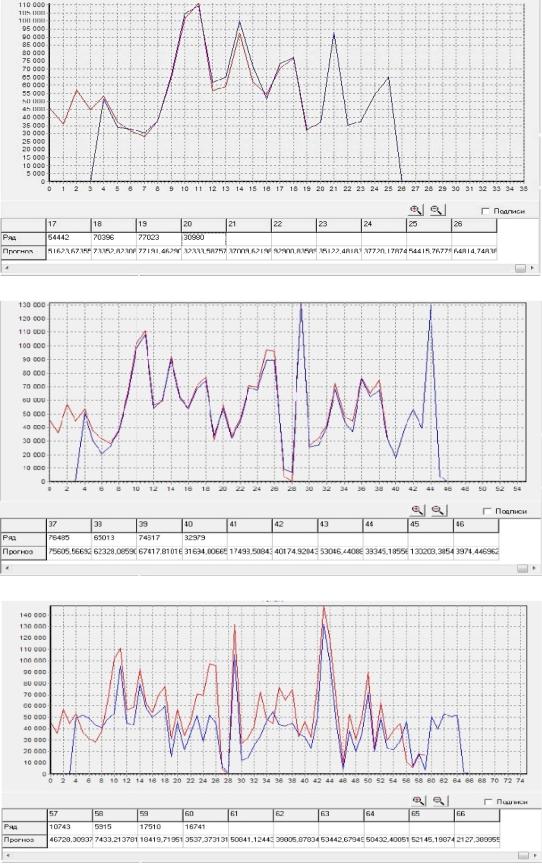
Рис. 2.48. Экранная форма с результатами прогноза для эксперимента №1

Рис. 2.49. Экранная форма с результатами прогноза для эксперимента №2

Рис. 2.50. Экранная форма с результатами прогноза для эксперимента №3

145

Визуальный анализ полученных результатов показывает, что точность прогнозных значений котировок зависит от структуры сети, в частности от числа используемых скрытых нейронных слоев. Наибольшая ошибка прогноза наблюдается в эксперименте №3, где используется один скрытый нейронный слой. Большей точностью обладает ИНС с двумя скрытыми нейронными слоями и увеличенным числом нейроновв них в эксперименте №2.

2.6.Модифицированный генетический алгоритмраспределения инвестиций

Основные трудности применения большинства методов оптимизации нелинейных унимодальных функций связаны с проблемами «проклятия размерности» и «застревания» в локальных экстремумах [34,59].

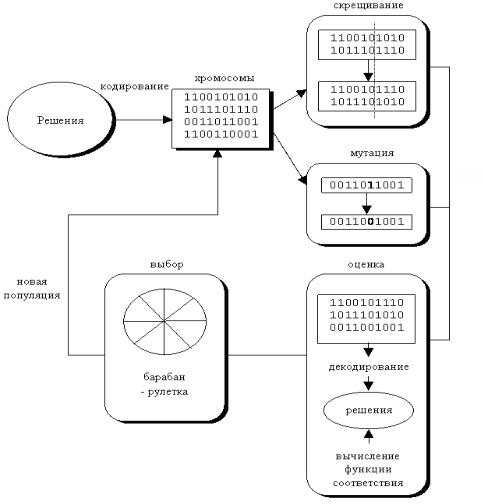
Одним из способов их преодоления является использование генетических алгоритмов (ГА). На основе механизма, представленного на рис. 2.51, они «выращивают» оптимальное решение.

Рис. 2.51. Механизм функционирования генетического алгоритма

ГА представляет собой одну из разновидностей случайного поиска [34], основанную на естественном отборе и размножении. Суть механизма его функционирования состоит в следующем. На первом этапе случайным образом формируется начальная популяция особей. В хромосоме (генотипе) каждой особи

146

закодировано возможное решение задачи (фенотип). Качество каждого решения оценивается функцией приспособленности (фитнес-функцией). На втором этапе осуществляется выбор особей и их скрещивание на основе оператора кроссовера. В результате формируется потомство, генетическая информация которого является результатом обмена хромосом родительских особей. На следующем этапе из особей вторичного потомства аналогичным образом формируется новое поколение. В данном поколении могут встречаться мутанты – особи со случайно измененными генотипами. Последнее реализуется на основе генетического оператора мутации. Эволюция популяции состоит из последовательности таких поколений [32].

Постановка задачи принятия инвестиционных решений в терминах ГА и последовательность ее решения представляются следующим образом.

Пусть задана сложная целевая функция (ЦФ) - суммарный доход инвестора, зависящая от нескольких переменных - объемов инвестиций в каждый проект. Требуется найти такие значения переменных, при которых ЦФ максимальна. Кроме того, заданы значения минимального и максимального объемов вложений в каждый из проектов, которые задают область изменения каждой из переменных.

Каждый вариант инвестирования (набор значений переменных) представляет собой особь. Его доходность – это приспособленность особи. В процессе эволюции приспособленность особей будет возрастать, что означает появление более доходных вариантов инвестирования. Остановив эволюцию в некоторый момент времени и выбрав наилучшую особь, будет получено хорошее решение задачи.

Функционирование ГА, применительно к решаемой задаче, представляет собой следующую последовательность действий.

РаботаГА начинается с формирования начальной популяции [53,209]:

P P1,P2 ,..., Pj ,..., PN ,

где j = 0, 1, 2, … – номер генерации ГА, N – размер популяции (количество особей в ней), который не изменяется в течение работы всего алгоритма.

Каждая особь генерируется как случайная L-битная строка, где L — длина кодировки особи, она тоже фиксирована, для всех особей одинакова и состоит из генов:

Pi g1,g2,..., g .

При выборе способа кодирования должно выполняться следующее условие: должна быть возможность закодировать (с допустимой погрешностью) в хромосоме любую точку из пространства поиска. Невыполнение этого условия может привести как к увеличению времени эволюционного поиска, так и к невозможности найти решение поставленной задачи.

Как правило, в хромосоме кодируются численные параметры решения. Для этого возможно использование целочисленного и вещественного кодирования. В данной работе использовались оба метода кодирования информации.

147

Рассмотрим целочисленное кодирование. Хромосома представляет собой битовую строку, в которой закодированы параметры решения поставленной задачи. На рис. 2.52 показан пример кодирования 4-х 10-разрядных параметров в 40–разрядной хромосоме. Принято считать, что каждому параметру соответствует свой ген. Следовательно, хромосома состоит из 4-х 10-разрядных генов.

Рис. 2.52. Пример целочисленного кодирования хромосомы

Несмотря на то, что каждый параметр в хромосоме закодирован целым числом, ему могут быть поставлены в соответствие и вещественные числа. Ниже представлен один из вариантов прямого и обратного преобразования «целочисленный ген - вещественное число».

Если известен диапазон, в пределах которого лежит значение параметра, то этот диапазон разбивают на 2m отрезков, где m - разрядность гена, и каждому отрезку соответствует определенное значение гена. При этом для перевода значений из закодированного значения в дробные применяют следующие формулы:

g r xmin 2m 1 ,

xmax xmin

где r – вещественное (декодированное) значение параметра; g – целочисленное (закодированное) значение параметра; xmax и xmin – максимальное и ми-

нимальное допустимое значение декодированного параметра [210,211]. Вещественное кодирование позволяет исключить операции кодирова-

ния/декодирования, используемые в целочисленном кодировании, и увеличить точность найденного решения.

Пример вещественного кодирования хромосомы представлен на рис. 2.53. После того, как сформирована и закодирована популяция, ГА начинает циклическую работу. Каждый его шаг состоит из трех стадий: генерацияпроме-

жуточной популяции - скрещивание особей - мутация.

Рис. 2.53. Пример вещественного кодированияхромосомы

148

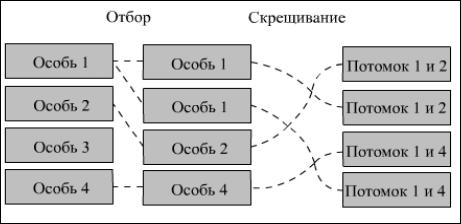
На рис. 2.54 изображены первые две стадии этого процесса.

Рис. 2.54. Генерация промежуточной популяции и скрещивание особей популяции

Промежуточная популяция – это набор особей, которые получили право размножаться. Приспособленные особи записываются несколько раз. «Плохие» особи исключаются из дальнейшего рассмотрения.

Генерация промежуточной популяции представляет собой процесс выбора K*N хромосом популяции G(t) для дальнейших генетических операций.

Выбор производится случайным образом. Вероятность выбора Sit хромо-

сомы пропорциональна её ценности.

Процесс выбора повторяется K*N раз. Предполагаемое количество экземпляров хромосомы Sit в популяции G(t+1) равно

nвыб Sit pвыб Sit K N .

Вероятность каждой особи попасть в промежуточную популяцию пропорциональна ее приспособленности, что соответствует пропорциональному отбору. Он реализуется несколькими способами.

Суть первого способа заключается в следующем. Пусть особи располагаются на колесе рулетки так, что размер сектора каждой особи пропорционален ее приспособленности. Изначально промежуточная популяция пуста. Запуская рулетку N раз, выберем требуемое количество особей для записи в промежуточную популяцию. Ни одна выбранная особь не удаляется с рулетки. Такой отбор называется стохастическим.

В другом способе отбора [226], который также является пропорциональным (рис.2. 55), для каждой особи вычисляется отношение ее приспособленности к средней приспособленности популяции. Целая часть этого отношения указывает на число требуемых записей особи в промежуточную популяцию, а дробная – на вероятность ее неоднократного попадания. Реализуется данный способ следующим образом. Расположим особи на рулетке как в первом способе. На рулетке есть N стрелок, отсекающих одинаковые сектора. Один запуск рулетки реализует выбор N особей, которые записываются в промежуточную популяцию.

149

Рис. 2.55. Пример пропорционального отбора

Операция воспроизводства увеличивает общую ценность последующей популяции путём увеличения числа наиболее ценных строк.

Пусть в популяции G(t) содержится n(H, t) хромосом, удовлетворяющих схеме H. Тогда в результате воспроизводства количество хромосом, удовлетворяющих схеме H в популяции G(t+1), будет равно n(H,t+1):

Используя выражения для средней ценности популяции Fср GH t и подпопуляции FсрGH t , формулу (2.80) можно записать в виде

N

Средняя ценность подпопуляции, соответствующей схеме H, может быть представлена в следующем виде:

Fср GH t Fср G t c Fср G t ,

где c – некоторая величина. Тогда формула (2.81) примет вид:

n H ,t 1 n H ,t K Fcp G t c Fcp G t / Fcp G t 1 c n H ,t K .

Предположим, что величина c при изменении t не изменяется. Тогда, начиная с t=0, получим:

n(H,t 1) n(H,0)*K*(1 c)t ,

т.е. в этом случае число представителей схемы (хромосом популяции G(t), соответствующих схеме) изменяется в геометрической прогрессии. Следовательно, процесс изменения представителей схемы аппроксимируется геометрической прогрессией.

Таким образом, в результате операции воспроизводства те схемы, для которых соответствующие подпопуляции имеют среднюю ценность выше средней в популяции, увеличивают количество своих представителей.

150