1 /N Рис. 1.5. Нерекурсивная схема реализации однородного ких-фильтра

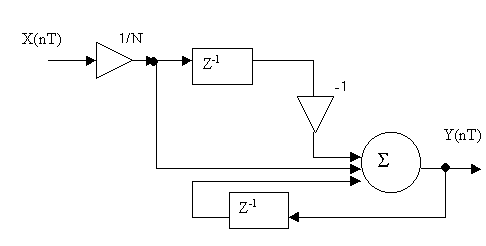
Рис. 1.6. Рекурсивная схема реализации однородного КИХ-фильтра

Очевидно, что передаточные функции (1.22) и (1.24) эквивалентны друг другу при любом значении z. Но, как можно заметить из выражения для передаточной функции рекурсивной реализации однородного фильтра, полюсы этой функции будут находиться непосредственно на единичной окружности на z-плоскости, то есть фильтр будет обладать очень малым запасом устойчивости. Это может привести к возникновению предельных циклов, так называемому «звону» фильтра, и в конечном итоге к его полной неработоспособности.

Если в (1.23) и (1.25) принято , то при реализации однородного фильтра не требуется выполнять операции умножения, поскольку умножение на сводится к p сдвигам на один разряд кода множимого.

Амплитудно-частотная характеристика однородного фильтра N-го порядка описывается формулой

. (1.26)

При проектировании КИХ-фильтров без операций умножения с точной линейной ФЧХ используется метод наименьших квадратов, согласно которому для КИХ-фильтра с передаточной функцией (1.4) и точно линейной ФЧХ при нечётном N можно согласно (1.22) получить

(1.27)

где

.

Метод наименьших квадратов позволяет рассчитать коэффициенты передаточной функции КИХ-фильтра с точно линейной ФЧХ по заданным требованиям к его АЧХ. В соответствии с этим методом при вспомогательные коэффициенты определяются из условия минимума целевой функции

, (1.28)

где функция удовлетворяет заданным условиям, функция определена в (1.27), - вектор коэффициентов , - весовая функция.

Весовая функция позволяет регулировать точность аппроксимации. Для тех интервалов частот, где значения весовой функции велики, точность аппроксимации оказывается выше, чем для тех интервалов частот, где значения весовой функции относительно малы. Более высокая точность аппроксимации соответствует «в среднем» большей близости друг к другу аппроксимируемой функции и аппроксимирующей функции и тем самым большей близости функции и АЧХ проектируемого фильтра .

Необходимые и достаточные условия минимума целевой функции (1.28) имеют вид

, (1.29)

и представляют собой систему линейных алгебраических уравнений относительно неизвестных коэффициентов

, (1.30)

где

.

Решив систему (1.30) и определив коэффициенты , можно рассчитать коэффициенты передаточной функции . Из (1.27) следуют соответствующие расчётные формулы:

. (1.31)

1.3.2. Фильтры с дискретными коэффициентами

Рассмотрим теперь различные способы реализации КИХ-фильтров без умножителей с дискретными коэффициентами.

Как уже было отмечено выше, особенностью современных ЦПОС является программная реализация операции умножения, выполнение которой поглощает большую часть его временных ресурсов. По этой причине при проектировании различных устройств цифровой обработки сигналов (в частности цифровых фильтров) основные усилия должны быть направлены на повышение производительности устройства.

Применительно к КИХ-фильтрам одним из наиболее эффективных способов решения указанной задачи является синтез передаточных функций с коэффициентами специального вида, конструкция которых облегчает выполнение операции умножения.

К конструкциям подобного вида отнесём следующие:

1. коэффициенты типа , i – целое, такие коэффициенты называются дискретными, умножение на дискретный коэффициент сводится к тривиальной операции сдвига;

2. коэффициенты, имеющие две единицы при каноническом знакоразрядном представлении, что достигается специальным группированием нулей и единиц при прямом двоичном кодировании

(1.32)

где - номера старшего и младшего разрядов в группе единиц; t – длина слова коэффициентов, при знакоразрядном представлении конструкция коэффициентов типа (1.32) позволяет заменить умножение на коэффициент, содержащий группу единиц в разрядах, двумя умножениями на и , последнее же достигается двумя сдвигами и одним сложением.

Если отсчёты сигналов ЦФ представлены в дополнительном коде, то умножение на достигается простым сдвигом кода на i разрядов в сторону младших разрядов, причём в освободившиеся разряды записывается значение старшего (знакового) разряда. Если коэффициенты ЦФ постоянны, то последовательность этих сложений можно определить непосредственно схемой ЦФ. На рис 1.7 для примера изображена схема такого ЦФ второго порядка, алгоритм работы которого описывается разностными уравнениями

(1.33)

,

где коэффициенты ЦФ записаны в знако-разрядном коде и в разряде i соответствует своему весу минус , а - отсчёты сигналов ЦФ для моментов времени n, n-1 и n-2.

В состав схемы предлагаемого на рис 1.7 ЦФ входят регистры, многовходовые сумматоры, ниверторы знака чисел и сдвигатели (умножители на ), соединения которых жёстко определяются видом реализуемого алгоритма. Многовходовые сумматоры можно построить на основе обычных двухвходовых сумматоров, причем их число равно p-1, где р – число входов многовходового сумматора. Инверторы знака чисел на выходе некоторых сдвигателей служат для умножения отсчётов на минус 1.

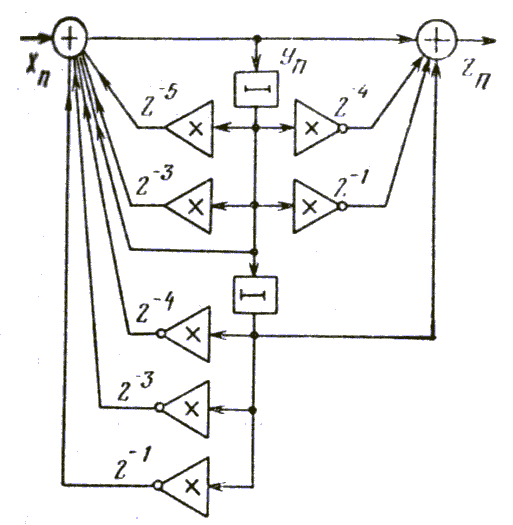
Рис. 1.7

Для уменьшения числа входов сумматоров (или иными словами, сокращения числа сложений) коэффициенты ЦФ необходимо преобразовать к такому виду, чтобы минимизировать число единичных элементов в двоичном коде коэффициента. Например, преобразуя коэффициент 0.1111 в 1.000 , можно перейти от четырёхвходового сумматора к двухвходовому. В ряде случаев сокращение числа сдвигателей также ведёт к упрощению схемы ЦФ. Для этого в коэффициентах при одинаковых отсчётах сигналов обеспечивается максимальное совпадение единичных элементов в соответствующих разрядах при сохранении общего числа единиц в кодах коэффициентов. Например, преобразуя коэффициент при , к виду .0101 в разностном уравнении (1.33), можно исключить из схемы ЦФ на рисунке 7 один сдвигатель. Получившаяся таким образом новая схема ЦФ приведена на рис. 1.8.

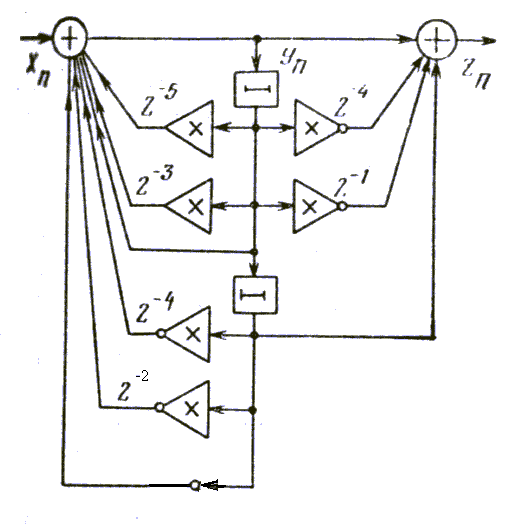
Рис. 1.8