
- •1. Исчисление высказываний
- •1.1. Алгоритмы проверки общезначимости и противоречивости в исчислении высказываний
- •1.2. Метод резолюций в исчислении высказываний
- •1.3. Метод резолюций для хорновских дизъюнктов
- •Задачи и упражнения
- •2. Логика и исчисление предикатов
- •2.1. Логика предикатов
- •2.2. Алгебра предикатов
- •2.2.1. Логические операции
- •2.2.2. Правила записи сложных формул
- •2.2.3. Законы алгебры предикатов
- •2.2.4. Предваренная нормальная форма
- •2.2.4.1. Алгоритм приведения формулы к виду пнф
- •2.2.5. Сколемовская стандартная форма
- •2.2.5.1. Алгоритм Сколема
- •2.3. Исчисление предикатов
- •2.3.1. Интерпретация формул
- •2.3.2. Правила вывода
- •2.3.3. Метод дедуктивного вывода
- •2.3.4. Метод резолюций в исчислении предикатов
- •2.4. Проблемы в исчислении предикатов
- •2.5. Логическое программирование
- •Задачи и упражнения
- •3. Элементы теории алгоритмов
- •3.1. Рекурсивные функции
- •3.1.1. Базовые функции
- •3.1.2. Элементарные операции
- •3.2. Машина Тьюринга
- •3.2.1. Описание машины Тьюринга
- •3.2.2. Примеры машин Тьюринга
- •3.2.3. Условные обозначения и схемные соединения машин Тьюринга
- •3.2.4. Рекурсивные функции и вычисления на машинах Тьюринга
- •3.3. Конечные автоматы
- •4. Неклассические логики
- •4.1. Пропозиционные логики
- •4.2. Алгоритмические логики
- •Задачи и упражнения
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
3.3. Конечные автоматы
Рассмотрим вкратце еще одну вычислительную модель, эквивалентную уже изученным моделям, – модель вычислений на конечных автоматах.
Детерминированным
конечным автоматом называется конечная
система
![]() где
где
Q – непустое множество состояний,
– непустой выходной алфавит,
![]() – функция
переходов,
– функция
переходов,
![]() – начальное
состояние,
– начальное
состояние,
![]() – множество
заключительных (принимающих) состояний,
– множество
заключительных (принимающих) состояний,
![]() – функция печати
(функция выходов).
– функция печати
(функция выходов).
Выберем некоторое
слово w=s1…sn
и зададим работу автомата М на слове
w. На первом шаге
автомат находится в начальном состоянии
q0 и после
прочтения первого символа s1
слова w определяется
состояние
![]() После этого автомат переходит в состояние
После этого автомат переходит в состояние
![]() и при наличии непустой информации,
выдаваемой значением
и при наличии непустой информации,
выдаваемой значением
![]() ,
это значение подается на выход. Продолжая
последовательность читать слово w
и определяя состояния
,
это значение подается на выход. Продолжая
последовательность читать слово w
и определяя состояния
![]() по функции t (где
по функции t (где
![]() ),
на каждом шаге выводится соответствующая
информация
),
на каждом шаге выводится соответствующая
информация
![]() (если она не пуста). Работа автомата
заканчивается после прочтения символа
(если она не пуста). Работа автомата
заканчивается после прочтения символа
![]() ,
не принадлежащего выходному алфавиту
, а если
слово w принадлежит
,
не принадлежащего выходному алфавиту
, а если
слово w принадлежит
![]() то после прочтения всего слова.
то после прочтения всего слова.
Входное слово w называется представимым автоматом М, если состояние, в которое переходит М после прочтения слова w, принадлежит множеству F.
Изображением
автомата М называется изображение
помеченного графа, состоящего из
множества вершин Q
с выделенными вершинами из множества
F, а также из
множества дуг
![]() где каждая дуга
где каждая дуга
![]() помечается символом sj,
который определяется из соотношения
помечается символом sj,
который определяется из соотношения
![]() а если
а если
![]() ,
то соответствующим словом
,
то соответствующим словом
![]() При этом каждая дуга может иметь несколько
таких меток, а вершина q0
дополнительно помечается входящей
дугой.
При этом каждая дуга может иметь несколько
таких меток, а вершина q0
дополнительно помечается входящей
дугой.
Пример. Рассмотрим конечный автомат М, изображенный на рис. 3.4. Автомат М имеет четыре вершины – q0, q1, q2, q3. При этом входящая вершина q0 выделена и образует одноэлементное множество заключительных состояний F. Функция печати для всех дуг выдает пустые значения, т. е. не дает никакой информации на выход.
 При
чтении слова
При
чтении слова
![]() автоматом М возникает последовательность
состояний q0q1q2q1q0q1.
Поскольку состояние q1
не является заключительным, слово w
не представимо автоматом М. Нетрудно
заметить, что произвольное непустое
слово
автоматом М возникает последовательность
состояний q0q1q2q1q0q1.
Поскольку состояние q1
не является заключительным, слово w
не представимо автоматом М. Нетрудно
заметить, что произвольное непустое
слово
![]() представимо в автомате М тогда и
только тогда, когда w
содержит четное число символов а и
четное число символов b.
представимо в автомате М тогда и
только тогда, когда w
содержит четное число символов а и
четное число символов b.
Пример. Рассмотрим конечный автомат М, изображенный на рис. 3.5.
Автомат М для любой пары чисел, записанных в двоичной системе счисления (т. е. для двух последовательностей нулей и единиц), вычисляет и выводит их сумму. При этом данные начинаются с битов, имеющих наименьшие разряды, и числа читаются справа налево. Недостатком автомата М является то, что он не распознает условий переполнения и не работает с отрицательными числами.
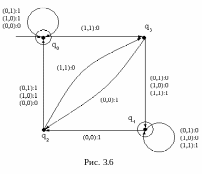
Пример. Конечный автомат М, изображенный на рис. 3.6 является модификацией автомата из предыдущего примера и позволяет на выходах q0 и q1 получать арифметически правильную сумму двоичных чисел. При этом с помощью состояний q2 и q3 проверяется наличие ошибок, связанных с внесением значений и знаковый бит и их вынесением из знакового бита.
Отметим, что
аналогично машинам Тьюринга любой
конечный автомат можно проинтерпретировать
в виде конечного автомата с алфавитом
![]()
Конечная система
![]() называется недетерминированным
конечным автоматом, если
называется недетерминированным
конечным автоматом, если
![]() – соответствующие элементы
детерминированного конечного автомата,
а функция переходов t
каждой паре
– соответствующие элементы
детерминированного конечного автомата,
а функция переходов t
каждой паре
![]() ставит в соответствие некоторое, не
обязательно одноэлементное, подмножество
множества
ставит в соответствие некоторое, не
обязательно одноэлементное, подмножество
множества
![]() т. е. выдает несколько значений из Q,
в которое может поместиться пара
(q,s).
т. е. выдает несколько значений из Q,
в которое может поместиться пара
(q,s).
 Таким
образом, отличие недетерминированного
конечного автомата состоит в том, что
функция переходов является многозначной.
Таким
образом, отличие недетерминированного
конечного автомата состоит в том, что
функция переходов является многозначной.
Использование недетерминированных конечных автоматов упрощает задачу построения сложных машин. Ниже будет установлено, что любой недетерминированный конечный автомат может быть естественным образом проинтерпретирован в виде детерминированного конечного автомата.
Определим множество
А(М) слов алфавита ,
представимых недетерминированным
конечным автоматом М. Пусть
![]() -
некоторое слово алфавита .
Определим по интуиции множество T(w),
положив
-
некоторое слово алфавита .
Определим по интуиции множество T(w),
положив
![]()
Очевидно, T(w)
– множество всех состояний автомата
М, которые могут быть достигнуты
под действием входного слова w.
Будем говорить, что слово w
представимо автоматом М, если
![]() .
Таким образом,
.
Таким образом,
![]() }.
}.
Теорема. Для любого недетерминированного конечного автомата М1 существует детерминированный конечный автомат М2 для которого А(М1)=А(М2).
Доказательство.
Рассмотрим недетерминированный конечный
автомат
![]() и построим детерминированный конечный
автомат
и построим детерминированный конечный
автомат
![]() с условием А(М1)=А(М2).
Положим
с условием А(М1)=А(М2).
Положим
![]()
Функцию p2 зададим произвольно, а функцию t2 определим по шагам:
1)
![]()
2)
![]()
3) если на шаге
некоторое значение
![]() уже определено, то
уже определено, то
![]()
4) на множествах
![]() ,
для которых значение
,
для которых значение
![]() не задается ни на каком шаге, описанном
в пп. 1 – 3, положим для определенности
не задается ни на каком шаге, описанном
в пп. 1 – 3, положим для определенности
![]() .
.
Непосредственно проверяем, что построенный таким образом детерминированный автомат М2 является искомым.
Задачи и упражнения
1. Доказать, что следующие функции есть примитивно рекурсивные:
a) f (х) = х + n; б) f (x) = n; в) f (x) = x !
2. Какие функции могут быть получены с помощью базовых и схемы примитивной рекурсии:
а) g (х) = J1,1; h (х; у; f (х; у)) = f+ (J3,1; J3,3);
б) g (х) = J1,1; h (х; у; f (х; у)) = f+ (J3,1; J3,2);
в) g (х) = J1,1; h (х; у; f (х; у)) = f+ (J3,2; J3,3);
3. Применить операцию минимизации к функции f по переменной у. Найти области определения и значения функции .
a) f (a; y) = [y/2]; б) f (x; y) = (x - 2y); в) f(x; y) = (x2 - 2y).
4. Построить машину Тьюринга для вычисления функций:
a) f (x) = x/2; б) f (x) = Sg x; в) f (x) = [x/2].
5. Какую функцию вычисляет машина Тьюринга со следующей программой команд:
Т : qí # q1 # n ;
qí | q1 # п ;
q1 # q2 # с ;
q1 | q1 | n .
