Е.Д. Федорков О.В. Собенина Н.Н. Свиридова

МАТЕМАТИЧЕСКАЯ ЛОГИКА

И ТЕОРИЯ АЛГОРИТМОВ

Учебное пособие

Воронеж 2005

Воронежский государственный технический

университет

Е.Д. Федорков О.В. Собенина Н.Н. Свиридова

МАТЕМАТИЧЕСКАЯ ЛОГИКА

И ТЕОРИЯ АЛГОРИТМОВ

Утверждено Редакционно-издательским советом университета

в качестве учебного пособия

Воронеж 2005

УДК 519.1

Федорков Е.Д., Собенина О.В., Свиридова Н.Н. Математическая логика и теория алгоритмов: Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2005. 125 с.

В учебном пособии излагаются основы современной математической логики и теории алгоритмов: исчисление высказываний, логика и исчисление предикатов, теория алгоритмов и неклассические логики. Каждый раздел иллюстрирован примерами, содержит задачи и упражнения для развития навыков решения основных типов задач. Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 654600 «Информационные системы», специальности 230202 «Информационные системы в образовании», дисциплине «Математическая логика и теория алгоритмов».

Издание может быть полезно студентам других технических специальностей, изучающих курс «Математическая логика и теория алгоритмов».

Табл. 7. Ил. 9. Библиогр.: 9 назв.

Рецензенты:

зам. директора ВНИИС по науке, д-р техн. наук И.И. Малышев; канд. физ.-мат. наук, доц. В.Н. Дурова

 Федорков Е.Д., Собенина О.В., Свиридова Н.Н., 2005

 Оформление. ГОУВПО

«Воронежский государственный

технический университет», 2005

ВВЕДЕНИЕ

Родоначальником науки о логике является греческий философ Аристотель (384-322 г. до н. э.). Он, используя законы человеческого мышления, формализовал известные до него правила рассуждений. Лишь в конце XVII века немецкий математик Г. Лейбниц предложил математизировать формальные рассуждения Аристотеля, вводя символьное обозначение для основных понятий и используя особые правила, близкие к вычислениям. Лейбниц утверждал, что «мы употребляем знаки не только для того, чтобы передать наши мысли другим лицам, но и для того, чтобы облегчить сам процесс нашего мышления».

Применение математики в логике определило новую науку – математическую логику. Математическое описание рассуждений позволило получить точные утверждения и эффективные процедуры в решении конкретных задач логики. Рассуждения в математической логике изучаются с точки зрения формы описания процесса, явления или события и формального преобразования этого описания. Такой процесс называют выводом заключения. Иногда математическое описание рассуждений называют логико-математическим моделированием.

Основными объектами при изучении математической логики являются формальный язык логики и правила вывода. Формальный язык необходим для символьного описания процессов, явлений или событий и логических связей между ними. Правила вывода необходимы для формирования процедуры рассуждения. Для обеспечения вывода вводится система аксиом, формализующая весь механизм вывода заключения.

Математическое описание логики следует воспринимать, как некую формальную систему, оперирующую с символами по определенным правилам, об­легчающим интерпретацию в реальном мире.

Выделяют несколько типов математических моделей формальной логики. Среди них можно выделить логику высказываний, логику предикатов, логику нечетких множеств и другие.

Логика высказываний (prepositional calculus) есть модель формальной системы, предметом которой являются высказывания или повествовательные предложения, взятые целиком без учета их внутренней структуры.

Логика предикатов (predicate calculus) есть модель формальной сис­темы, предметом которой являются повествовательные предложения с учетом их внутренних состава и струк­туры.

Логика нечетких множеств и отношений (fuzzi calculus) есть модель формальной системы, предметом кото­рой являются повествовательные предложения с учетом их внутренних состава и структуры и при нечетком (размытом) задании характер­ных признаков отдельных элементов или отношений между ними.

Математическая логика рассматривает формальный способ рассуждения, встречающийся не только в математике, но и в повседневной жизни.

Теория алгоритмов – раздел математики, изучающий общие свойства алгоритмов. Содержательные явления, приведшие к образованию понятия алгоритма, прослеживаются в математике в течение всего времени ее существования. Однако само это понятие сформировалось лишь в двадцатом веке в связи с вопросами о границах вычислимости.

Бурное развитие математической логики и теории алгоритмов во многом обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представление моделей на компьютерах.

1. Исчисление высказываний

Для алгебры высказываний существует в известном смысле адекватная аксиоматическая логическая система, которая называется исчислением высказываний. Описание всякого исчисления заключает в себе описание символов этого исчисления, формул, являющихся конечными конфигурациями символов, и после этого определение истинных формул (или выводимых формул).

Выводом в исчислении называется последовательность формул такая, что для любого i формула X_i есть либо аксиома исчисления, либо непосредственное следствие каких-либо предыдущих формул.

Формула Y называется теоремой исчисления, выводимой в исчислении или доказуемой в исчислении, если существует вывод ,Y, который выводом формулы Y или доказательством теоремы Y.

Вообще говоря, может не существовать алгоритма, с помощью которого для произвольной формулы через конечное число шагов можно определить, является ли она выводимой в исчислении или нет. Если такой алгоритм существует, то исчисление называется разрешимым.

Символами исчисления высказываний являются во-первых, заглавные латинские буквы, с индексами или без, которыми обозначаются высказывания, во-вторых, знаки логических операций и, в-третьих, пара скобок ( ). Иных символов, кроме указанных, исчисление высказываний не имеет. Формулы исчисления высказываний представляют собой конечные последовательности описанных символов. Эти последовательности, как правило, записываются в виде строчек. Не всякая строка символов является формулой. Полное определение формулы имеет рекурсивный характер: указываются некоторые исходные формулы и затем правила, позволяющие из формул образовывать новые формулы. Таким образом, определение формулы можно сформулировать следующим образом:

1. Переменное высказывание есть формула (элементарная формула).

2. Если X и Y – формулы, то 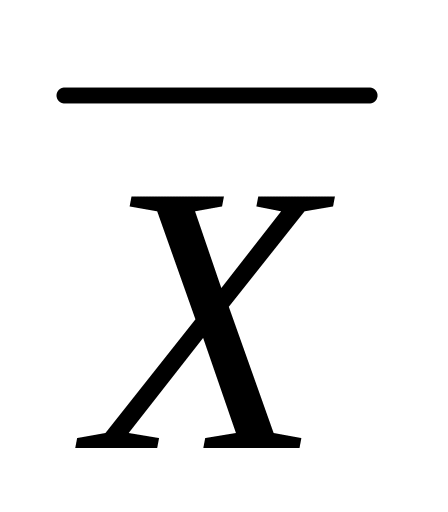, X  Y, X  Y, X  Y

также формулы.

Для доказательства того, что некоторая последовательность символов является формулой, необходимо показать, что она удовлетворяет определению формулы, т. е. требуется произвести ее конструкцию по указанной в определении схеме, так что при построении формулы мы должны построить и все ее части, называемые подформулами.

Пример. Чтобы доказать, что последовательность ((X  Y)  (X  Z)) является формулой, мы должны рассуждать следующим образом: так как X и Y формулы, то (X  Y) – также формула, так как X и Z – формулы, то (X  Z) – также формула; так как (X  Y) и (X  Z) – формулы, то

((X  Y)  (X  Z)) – также формула.

Следующим шагом в определении исчисления высказываний является определение некоторого класса формул, которые называются истинными или выводимыми в исчислении высказываний. Определение истинных формул имеет такой же рекурсивный характер, как и определение формулы. Сначала определяются исходные истинные формулы, а затем определяются правила, позволяющие из имеющихся истинных формул образовывать новые. Эти правила называются правилами вывода, а исходные истинные формулы – аксиомами. Образование истинной формулы из исходных истинных формул или аксиом путем применения правил вывода называется выводом данной формулы из аксиом.

Для полного набора логических связок: импликация, отрицание, конъюнкция и дизъюнкция система содержит десять аксиом. В силу полноты систем, использующих логические связки а) импликации и отрицания, б) импликации и дизъюнкции, в) импликации, отрицания, конъюнкции и дизъюнкции можно использовать в процессе дедуктивного вывода любую из указанных систем.

Ниже приведена одна из систем аксиом:

1. ├─X(YX);

2. ├─(XY)((X(YZ))(XZ));

3. ├─XYX;

4. ├─XYY;

5. ├─(XY)((XZ)(XYZ));

6. ├─XXY;

7. ├─YXY;

8. ├─(XZ)((YZ)(XYZ));

9. ├─(XY)((X ) );

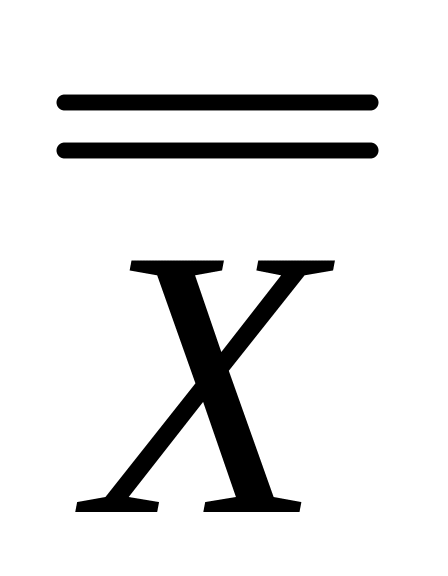10. ├─ X;

Как видно из приведенного списка, аксиомы разбиваются на четыре группы {1, 2}, {3, 4, 5}, {6, 7, 8}, {9, 10}. Аксиомы первой группы содержат только импликацию, причем эта логическая связка входит и в остальные группы. Но во второй группе к импликации добавляется конъюнкция, в третьей – дизъюнкция, а в четвертой – отрицание.

К правилам вывода в исчислении высказываний относятся следующие:

1. Правило подстановки. Пусть А – формула, содержащая букву Х. Тогда А истинная формула в исчислении высказываний, то заменяя в ней букву Х всюду, где она входит, произвольной формулой В, мы также получаем истинную формулу.

Если выводимая формула F содержит некоторую переменную A (обозначим этот факт F(A)) и существует произвольная формула B, то формула F(B), получающаяся заменой всех вхождений A на формулу B, также выводима в исчислении высказываний. Этот факт формально описывают так:

Этот факт записывают так: .

Если F(A)=A, то

Если , то

Следует еще раз обратить внимание, что формула F должна быть выводимой в исчислении высказываний.

Пример. Пусть даны формулы F=ACA и B=C .

Если выполнить подстановку формулы B в формулу F вместо формулы A, то получим новую формулу F`.

2. Правило заключения. Если А и А  В – истинные формулы в исчислении высказываний, то В также истинная формула.

Пример. Если формулы истинны и , то формула тоже истинна.

Указанием аксиом и правил вывода мы полностью определяем понятие истинной или выводимой в исчислении высказываний формулы. Пользуясь правилами вывода, мы можем исходя из аксиом, конструировать новые истинные формулы и получать таким образом каждую истинную формулу. Кроме основных правил вывода – правила подстановки и правила заключения, существуют и другие правила образования истинных формул, производные от основных правил и являющиеся сокращением многократного применения основных правил. Правила выражаются обычно в следующих терминах: «если формулы А, В, ... истинны, то формулы Х, Y, ... также истинны» и записываются в виде .

Будем говорить, что формула Y выводима из формул X₁, X₂,..., X_n , если формулу Y можно вывести только путем правила заключения, приняв за исходные формулы X₁, X₂,..., X_n и все истинные в исчислении высказываний формулы. Точное определение выводимости формулы Y из формул X₁, X₂,..., X_n, называемых исходными, формулируется следующим образом:

1. Каждая формула X_i (1  i  n) выводима из формул X₁, X₂,..., X_n.

2. Каждая истинная в исчислении высказываний формула выводима из X₁, X₂,..., X_n.

3. Если формулы X и X  Y выводимы из X₁, X₂,..., X_n, то формула Y также выводима из X₁, X₂,..., X_n.

Утверждение, что формула Y выводима из формул X₁, X₂,..., X_n обозначается в виде X₁, X₂,..., X_n ├─ Y.

Замечание 1. Выводимость формулы Y из формул X₁, X₂,..., X_n отличается от выводимости истинной формулы из аксиом исчисления высказываний тем, что во втором случае в числе правил вывода имеется правило подстановки, которого нет в первом случае. Можно было бы определить и такую выводимость формулы Y из формул X₁, X₂,..., X_n, в которой правило подстановки имело бы место.

Замечание 2. Если X₁, X₂,..., X_n являются аксиомами или истинными формулами, то класс выводимых из них формул совпадает с классом всех истинных формул, так как всякая истинная формула считается выводимой из любой системы формул.

Расширим понимание выражения X₁, X₂,..., X_n ├─ Y на случай, когда формулы X₁, X₂,..., X_n отсутствуют, считая, что тогда Y является просто истинной формулой исчисления высказываний. Этот факт обозначается в виде ├─ Y и равносилен тому, что Y – теорема исчисления высказываний.

Пример. Покажем, что формула выводима в исчислении высказываний. Для этого построим вывод данной формулы:

1. в схеме аксиом 2 Y заменим на , Z – на X. Получим ;

2. в схеме аксиом 1 Y заменим на X. Получим ;

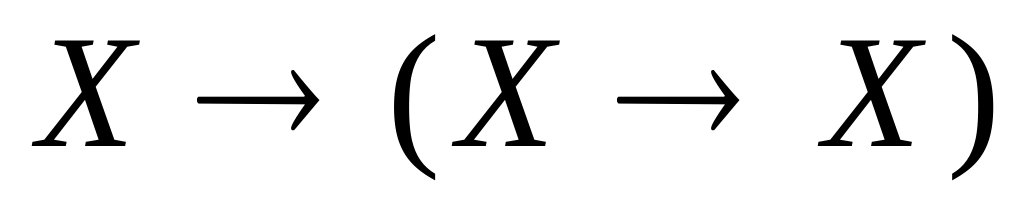3. из 1 и 2 по правилу заключения получим

;

4. в схеме аксиом 1 заменим Y на , получим

;

5) из 3 и 4 по правилу заключения справедливо ├─ .

Для того чтобы установить выводимость различных формул более простым путем, чем непосредственный вывод этих формул, используется так называемая теорема дедукции.

Теорема дедукции. Если формула Y выводима из формул X₁, X₂,..., X_n , то X₁ (X₂  (...(X_n  Y) ...)) истинная формула.

С помощью теоремы дедукции можно получать новые правила исчисления высказываний.

Пример. Рассмотрим формулы X  (Y  Z), Y, X.

Применяя два раза правило заключения, находим, что

X  (Y  Z), Y, X ├─ Z.

Применяя теорему дедукции, получим правило

├─ (X  (Y  Z))  (Y  (X  Z)),

которое носит название правила перестановки посылок.

Используя правила эквивалентных преобразований алгебры высказываний, можно показать дедуктивный характер вывода заключения:

1) ├─ (X₁X₂...X_nY);

2) ├─ ( Y);

3) ├─ (  ... Y);

4) ├─ (  ... (X_nY));

5) ├─ (  ...( X_n-1(X_nY)));

6) ├─ (  ( X₂ ...(X_n-1(X_nY))...));

7) ├─ (X₁(X₂ ...(X_n-1(X_nY))...).

Так формируется система де­дуктивного вывода от по­сылок до заключения.

Замечание 3. Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого свободные переменные исчисления высказываний будем трактовать как переменные алгебры высказываний, то есть переменные, принимающие значения «истина» или «ложь». Операции , , ,  определим также, как в алгебре высказываний. Тогда всякая формула при любых значениях переменных сама будет принимать одно из значений «истина» или «ложь», вычисляемое по правилам алгебры высказываний.

Теорема (о полноте). Формула Y доказуема тогда и только тогда, когда Y тождественно истинна.

Таким образом, для того чтобы установить, доказуема ли формула, достаточно составить ее таблицу истинности. Как известно, существует алгоритм построения таблицы истинности, и, значит, исчисление высказываний разрешимо.

Для проверки тождественной истинности аксиом рассмотри, например, таблицу истинности для аксиомы 8:

├─(XZ)((YZ)(XYZ)).

Х	Y	Z	1 2	13	23	43	67	58
1	2	3	4	5	6	7	8	9
0	0	0	0	1	1	1	1	1
0	0	1	0	1	1	1	1	1
0	1	0	1	1	0	0	1	1
0	1	1	1	1	1	1	1	1
1	0	0	1	0	1	0	0	1
1	0	1	1	1	1	1	1	1
1	1	0	1	0	0	0	1	1
1	1	1	1	1	1	1	1	1

Логическое исчисление называется непротиворечивым, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой. Иными словами, непротиворечивое исчисление – это такое исчисление, что какова бы ни была формула X, никогда формулы X и не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил. Проблема непротиворечивости состоит в следующем: является ли данное исчисление непротиворечивым или нет?

Для исчисления высказываний можно показать, что все аксиомы являются тождественно истинными формулами, а применяя к тождественно истинным формулам правила вывода, получим также тождественно истинные формулы. Следовательно, все выводимые формулы исчисления высказываний, рассматриваемые как формулы алгебры высказываний, являются тождественно истинными, что показывает непротиворечивость исчисления высказываний.

Теорема (о непротиворечивости). Исчисление высказываний непротиворечиво.

Доказательство. По теореме о полноте любая формула, не являющаяся тождественно истинной, не доказуема в исчислении высказываний. Например, такой формулой является формула .

Однако возникает обратный вопрос: будет ли всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний? Этот вопрос представляет собой проблему полноты в широком смысле для исчисления высказываний. Смысл этой постановки вопроса состоит в том, что при построении логического исчисления, предназначенного выражать содержательную логику, нам требуется знать, достаточно ли мы имеем аксиом и правил для того, чтобы вывести любую формулу, которая в содержательном понимании является тождественно истинной. Проблема полноты в широком смысле решается положительным образом: всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний.

Не менее важное значение, чем понятие полноты в широком смысле, имеет понятие полноты логического исчисления в узком смысле. Логическое исчисление называется полным в узком смысле, если присоединение ее аксиомам какой-нибудь не выводимой в ней формулы приводит к противоречию. Для исчисления высказываний проблема полноты в узком смысле также решается положительно.