Е. А. Ровба - Высшая математика

Добавил:

Ivanoff228 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

Высшая математика

Файл:

руемой на этом отрезке, причем

Φ (x) = *ax f(t) dt

Д о к а з а т е л ь с т в о. Достаточно доказать, что существует

Φ(x + x) − Φ(x)

.pdf

Скачиваний:

181

Добавлен:

21.01.2022

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 4128 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>

270	Глава 5. Теория интегрирования

Произведем разбиение отрезка [a, b]:

a = x0 < x1 < x2 < . . . < xk−1 < xk < . . . < xn = b.

Составим интегральную сумму:

σ = D(ξk)Δxk.

k=1

Покажем, что предел интегральных сумм при

λ = max (xk − xk−1) → 0

1 k n

не существует. Действительно, если выбрать все ξk иррациональными, то σ = 0, если же выбрать все ξk рациональными, то

σ = xk = b − a = 0.

k=1

Это означает, что предел интегральных сумм σ при λ → 0 не существует, т.е. функция Дирихле не интегрируема на любом отрезке

[a, b].

5.3.5.Достаточные условия интегрируемости функции

Теорема 5.6. Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Отметим, что условие непрерывности функции является достаточным условием, но не необходимым.

Можно показать, в частности, что справедливы следующие утверждения.

Теорема 5.7. Если функция f ограничена на отрезке [a, b] и имеет конечное число точек разрыва, то она интегрируема на этом отрезке.

Теорема 5.8. Если функция f ограничена и монотонна на отрезке [a, b], то она интегрируема на этом отрезке.

5.3. Определенный интеграл	271

Например, функция f(x) = x cos2 x + ex является интегрируемой на любом отрезке [a, b], так как она непрерывна на R.

Функция f(x) = sign x (см. формулу (3.7)) является интегрируемой на отрезке [−1, 1], так как только в точке x = 0 она имеет точку разрыва первого рода.

Функция f(x) = 1/x при x (0, 1] и f(0) = 0 не является интегрируемой на отрезке, потому что она не ограничена на отрезке

[0, 1].

5.3.6.Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функции

Важную роль в интегральном исчислении играет связь между определенным и неопределенным интегралами. Перейдем к ее исследованию.

Пусть функция f является интегрируемой на отрезке [a, b]. Фиксируем x [a, b].

Функция f будет интегрируемой на отрезке [a, x], т.е. существует

интеграл

f(t) dt.

Теперь каждому x [a, b] поставим в соответствие число, равное

f(t) dt.

a
Это означает, что на отрезке [a, b] будет определена функция
*x	(5.28)
Φ(x) = f(t) dt.	(5.28)

Определение 5.7. Функция Φ(x), задаваемая формулой (5.28), называется интегралом с переменным верхним пределом.

272	Глава 5. Теория интегрирования

Геометрический смысл интеграла с переменным верхним пределом состоит в том, что данный интеграл численно равен площади криволинейной трапеции, расположенной над отрезком [a, x] (рис. 5.5).

y
		y = f(x)
		S(x)
O	a	x	b x
		Рис. 5.5

Теорема 5.9. Если функция f непрерывна на отрезке [a, b], то функция Φ, определяемая формулой (5.28), является дифференци-

Из определения функции Φ(x) и свойства определенного интеграла следует:

		x+Δx			x		x+Δx
Φ(x + x) =		*a	f(t) dt = *a			f(t) dt +	*x	f(t) dt.
Значит,
x				x+Δx		x+Δx			x+Δx
Φ(x + x) − Φ(x) = *	f(t) dt +			*	f(t) dt − *		f(t) dt =		*	f(t) dt.

5.3. Определенный интеграл	273

К полученному интегралу применим теорему о среднем значении. Будем иметь:

Φ(x + x) − Φ(x) = f(c)Δx,

где c — некоторая точка, заключенная между x и x +						x. Тогда
	Φ(x + x) − Φ(x)	= f(c),	lim	Φ(x +	x) − Φ(x)	= lim f(c).

	x				x
			x→0			x→0

Теперь заметим, что если x → 0, то и c → x, поэтому в силу непрерывности функции f в точке x [a, b] имеем:

lim f(c) = f(x).

x→0

Иначе говоря, теорема 5.9 утверждает, что производная от интеграла с переменным верхним пределом равна значению подынтегральной функции в точке, равной верхнему пределу.

Теорему 5.9 можно переформулировать следующим образом:

если функция f непрерывна на отрезке [a, b], то

Φ(x) = f(t) dt

является ее первообразной на этом отрезке. Следовательно,

f(x) dx = Φ(x) + C.

5.3.7. Формула Ньютона — Лейбница

Формула Ньютона — Лейбница считается основной формулой интегрального исчисления. Она позволяет свести вычисление определенного интеграла от непрерывной функции к вычислению разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования.

274	Глава 5. Теория интегрирования

Теорема 5.10. Если функция f(x) непрерывна на отрезке [a, b] и F (x)— какая-либо ее первообразная, то справедлива формула Ньютона — Лейбница

f(x) dx = F (b) − F (a).

(5.29)

Д о к а з а т е л ь с т в о. Пусть F (x) — какая-либо первообразная

для непрерывной функции f на отрезке [a, b]. По теореме 5.9 функция

Φ(x) = f(t) dt также является первообразной для f на отрезке

[a, b]. Поскольку любые две первообразные для функции f могут различаться лишь на постоянную (теорема 5.1), то

Φ(x) = F (x) + C,

x [a, b],

C = const .

(5.30)

Положив в формуле (5.30) x = a, получим: Φ(a) = F (a) + C. Но очевидно, что Φ(a) = 0. Значит, C = −F (a), поэтому равенство (5.30) можно записать в виде

f(t) dt = F (x) − F (a).

Теперь положим здесь x = b и получим формулу Ньютона — Лейбница (5.29).

Разность F (b) − F (a) принято обозначать F (x) ba. Тогда формулу Ньютона — Лейбница можно записать в виде

a	b		b
*


		f(x) dx = F (x) a.
		π/4
Пример 5.21. Вычислить интеграл *			sin 2x dx.

5.3. Определенный интеграл	275

Р е ш е н и е. Одной из первообразных для функции f(x) = sin 2x является функция F (x) = −1/2 cos 2x, поэтому, применяя формулу Ньютона — Лейбница, имеем:

π/4
0	1		1		π		1
*

	sin 2x dx = − 2 cos 2x	0	= − 2	cos 2		− cos 0 = 2 .

5.3.8.Замена переменной и интегрирование по частям в определенном интеграле

Теорема 5.11. Пусть функция f(x) непрерывна на отрезке [a, b], а функция x = ϕ(t) имеет непрерывную производную на отрезке [α, β], причем отрезок [a, b] является множеством значений функции x = ϕ(t) и ϕ(α) = a, ϕ(β) = b. Тогда справедлива формула

*b	*β
f(x) dx =	f(ϕ(t))ϕ (t) dt.	(5.31)

aα

До к а з а т е л ь с т в о. Пусть F — первообразная для функции f:

F (x) = f(x), x [a, b].
Тогда
*b f(x) dx = F (b) − F (a).	(5.32)

Положим G(t) = F (ϕ(t)). По правилу дифференцирования сложной функции получим:

G (t) = F (ϕ(t))ϕ (t) = f(ϕ(t))ϕ (t).

Следовательно, функция G(t) есть первообразная для функции f(ϕ(t))ϕ (t) на отрезке [a, b], и по формуле Ньютона — Лейбница находим:

*β

f(ϕ(t))ϕ (t) dt = G(β) − G(α) =

= F (ϕ(β)) − F (ϕ(α)) = F (b) − F (a). (5.33)

276	Глава 5. Теория интегрирования

Правые части равенств (5.32) и (5.33) совпадают. Сравнив их
левые части, получим формулу (5.31).
Формула (5.31) называется формулой замены переменной в опре-
деленном интеграле.
Пример 5.22. Найти интеграл *1		√	x	dx.

			1 x2
0			−
Р е ш е н и е. Воспользуемся формулой замены переменной. По-

ложим 1 − x2 = t, −2x dx = dt. Очевидно, что 1 − 02 = 1, 1 − 12 = 0. По формуле (5.31)

√

dx = −

√

dt =

√

dt =

2√t 0 =

√1 −

√0 = 1.

1 x2

−

В этом случае можно поступить и по-другому. Положим x

= sin t,

= cos t dt. Очевидно, что sin 0

= 0, sin(π/2) = 1. Отрезок [0, 1]

является множеством значений функции x

sin t, t

[0, π/2]. По

формуле (5.31)

π/2

√

dx =

sin

cos t dt = *

sin t dt = cos t 0

= 1.

1 x2

1 sin2 t

−

Подчеркнем два важных момента. Во-первых, при использовании формулы замены переменной (5.31) в интеграле справа следует найти и поставить новые пределы интегрирования. Во-вторых, здесь в отличие от неопределенного интеграла нет необходимости возвращаться к старой переменной.

Теорема 5.12. Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула

b	b	b
a		a

*		− *	v du.	(5.34)
	u dv = uv a

5.3. Определенный интеграл	277

Д о к а з а т е л ь с т в о. Очевидно, что функция u(x)v(x) является первообразной для функции v(x)u (x) + u(x)v (x), так как

(u(x)v(x)) = v(x)u (x) + u(x)v (x).

Следовательно,

*b b

(v(x)u (x) + u(x)v (x)) dx = (u(x)v(x)) ,

или

b		b	b
a			a
*			− * (v(x)u (x).
	u(x)v (x) dx = (u(x)v(x)) a

В силу того что u (x) dx = du, v (x) dx = dv, эту формулу можно записать в виде (5.34).

Формулу (5.34) называют формулой интегрирования по частям в определенном интеграле.

Пример 5.23. Найти интеграл xex dx.

Р е ш е н и е. Применим формулу интегрирования по частям:

1	1	1	1
		1

*	xex dx = *				1
*	xex dx = *	x dex = xex	0	−	*	ex dx =	1
0	0				0		1
0	0				0
					0
		= e −			*			= e − (e − 1) = 1.
		= e −			*	ex dx = e − ex 0		= e − (e − 1) = 1.

278	Глава 5. Теория интегрирования

5.4.Приложения определенного интеграла

5.4.1. Площадь криволинейной трапеции

В § 5.3 уже отмечалось, что определенный интеграл

f(x) dx

от неотрицательной функции f численно равен площади криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми x = a, x = b и y = 0.

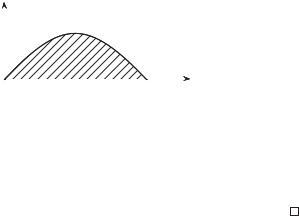
Пример 5.24. Вычислить площадь фигуры, заключенной между осью Ox и синусоидой y = sin x, x [0, π] (рис. 5.6).

	y	y = sin x
	y
	1



	O				π	x
		Рис. 5.6
		Рис. 5.6
Р е ш е н и е. Находим:
π			π
0			π
S = *				=	−(cos π − cos 0) = 2.
S = *	sin x dx = − cos x 0			=	−(cos π − cos 0) = 2.

Если фигура не является криволинейной трапецией, то ее площадь стараются представить в виде суммы или разности площадей фигур, являющихся криволинейными трапециями. В частности, справедлива следующая теорема.

5.4. Приложения определенного интеграла								279
Теорема 5.13. Если фигура ограничена снизу и сверху гра-
фиками непрерывных функций y = f1(x), y = f2(x) (не обязатель-
но неотрицательных (рис. 5.7)), то ее площадь можно найти по
формуле
	S = ab f2(x) dx − ab f1(x) dx.
			y
y	y = f2(x)
	y = f2(x)
			4
					=	x
				y	=
				y				x = 4
			2					x = 4
			2
	a				xy = 4
O			x		xy = 4
O		b	x
	y = f1(x)	b	O					x
				2			4	x
				2			4
	Рис. 5.7			Рис. 5.8

Пример 5.25. Вычислить площадь фигуры, ограниченной кривой xy = 4 и прямыми y = x, x = 4.

Р е ш е н и е. Построим фигуру на плоскости (рис. 5.8). Очевидно, что f1(x) = 4/x, f2(x) = x. Тогда

4		x2		4
2
4

S = * x − x dx =	2		− 4 ln x 2		=

=8 − 4 ln 4 − (2 − 4 ln 2) = 2(3 − 2 ln 2).

5.4.2.Длина дуги кривой

Вычисление длин кривых также приводит к интегралам. Пусть функция y = f(x) непрерывна на отрезке [a, b] и дифференцируема

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 4128 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>