2.3.2. Условия равновесия плоской системы пар.
Если момент результирующей пары M=0, то твердое тело будет находиться в равновесии, при этом
Для равенства плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы была равна нулю.
2.4. Приведение произвольной плоской системы сил к заданному центру.
Совокупность сил, расположенных на плоскости как угодно, называется произвольной плоской системой сил.
Пользуясь теоремой Пуансо, можно любую произвольную плоскую систему сил привести к произвольно выбранному центру.
Пусть имеется произвольная плоская
система сил
.
Выберем произвольно центр приведения
(т. O).
,
– главный вектор произвольной плоской
системы сил.
Главный вектор приложен в центре приведения, причем его величина и направление не зависят от места выбора центра приведения, т. к. сложение геометрическое.
Вопросы для самоконтроля
Момент силы относительно точки на плоскости.
Пара сил и ее основные свойства.
Момент пары сил.
Приведение плоской системы сил к данному центру (метод Пуансо).
Главный вектор и главный момент.
Частные случаи приведения произвольной плоской системы сил.
Аналитические условия равновесия произвольной плоской системы сил.
Теорема Вариньона.
Лекция 3
ФЕРМЫ
3.1. Понятие о ферме. Статическая определимость ферм.
Фермой называется жесткая конструкция, состоящая из прямолинейных стержней, соединенных между собой шарнирами.
Точки, где сходятся оси стержней, называются узлами. Те узлы, которыми ферма опирается на основание, называются опорными узлами.
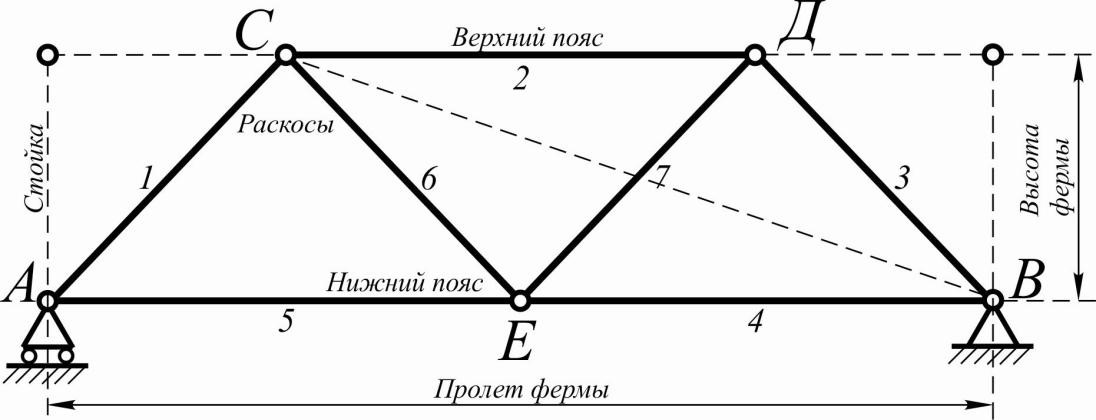
Вертикальные стержни называются стойками, а наклонные - раскосами.
Стержни, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру - нижний пояс фермы.
Если оси всех стержней фермы лежат в одной плоскости, то ее называют плоской фермой.
Для упрощения расчетов ферм вводятся следующие допущения:
Крепление стержней шарнирное.
Трение в шарнирах отсутствует.
Весом стержней пренебрегают.
Все нагрузки сосредоточены в узлах фермы.
Ферма с такими допущениями называется теоретической. В такой ферме каждый стержень будет испытывать только усилие сжатия или растяжения.
Реальные фермы не имеют таких идеальных шарниров, однако, такое допущение облегчает вычисление усилий в стержнях фермы.
Если, при снятии с фермы хотя бы одного стержня, она теряет свою жесткость, то эта ферма без лишних стержней.
Ферма без лишних стержней должна удовлетворять следующему условию:
где: m- число стержней, n- число узлов.
Если, при снятии с фермы одного или нескольких стержней, она не теряет свою жесткость, то эта ферма с лишними стержнями. В этом случае
Такие фермы имеют повышенную металлоемкость при той же жесткости.
Если
,
то фермы нет, а есть геометрически
изменяющаяся конструкция.
Расчет фермы заключается в определении опорных реакций и усилий в стержнях.
При этом опорные реакции и заданные нагрузки, действующие на ферму, являются внешними силами, а усилия в стержнях - внутренними.
Если все неизвестные опорные реакции и усилия в стержнях могут быть определены из уравнений статики, то ферма называется статически определимой, в противном случае - нет.
Условие статической определимости фермы имеет вид:
где: m- число стержней, n - число узлов.
Т. е. статически определимая ферма - ферма без лишних стержней.