1.4. Аксиома связей (принцип освобождаемости от связей)

Всякое несвободное тело можно рассматривать как свободное, если отбросить связи, наложенные на него, и заменить их действие реакциями этих связей

1.5. Система сходящихся сил на плоскости.

Системой сходящихся сил называется совокупность сил, линии действия которых пересекаются в одной точке.

Система сходящихся сил может быть плоской и пространственной.

1.5.1. Сложение двух сходящихся сил

Сложить систему сходящихся сил – значит найти их равнодействующую силу по модулю, направлению и найти точку ее приложения.

Существует два правила сложения 2-х сил: 1) правило параллелограмма.

сходящихся сил является диагональю параллелограмма, построенного на этих силах. 2) правило треугольника.

Равнодействующая 2-х сходящихся сил является замыкающей стороной силового треугольника, построенного на этих силах.

Для определения используют известные формулы из тригонометрии, для чего в условиях задачи должны быть заданы углы.

1.5.2. Геометрические условия равновесия плоской системы сходящихся сил

Плоская система сходящихся сил будет находиться в равновесии, если их равнодействующая (главный вектор) равна 0, т. е. силовой многоугольник должен быть самозамыкающимся.

В замкнутом силовом многоугольнике сил все силы направлены по контуру многоугольника в одну сторону по обходу многоугольника.

Частный случай: три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.

Условие равновесия сходящихся сил, расположенных в пространстве и на плоскости, одно и то же. Однако, графический метод решения задач на систему сходящихся сил практически применяется только для сил, расположенных в одной плоскости.

1.5.2.1. Проекция силы на ось и на плоскость

Проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного на оси между перпендикулярами, опущенными из конца и начала вектора силы.

F_x Fcos .

Проекция силы на ось равна произведению модуля силы на cos угла между положительным направлением оси и направлением вектора силы.

О чевидно, что если , то F_x0,

, то F_x0,

, то Fx0,

2

1.5.2.2. Теорема о проекции равнодействующей силы на ось. Аналитический способ сложения системы сходящихся сил на плоскости

Проекция равнодействующей некоторой системы сходящихся сил на ось равна алгебраической сумме проекций составляющих сил на ту же ось.

На ось x:

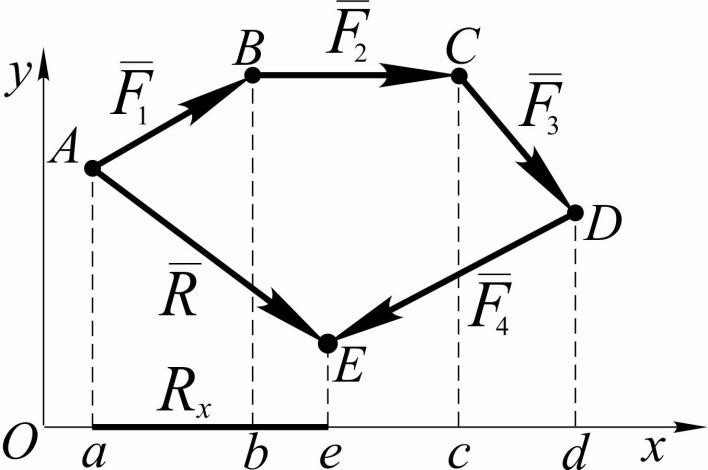
R_x

(1)

1.5.3. Аналитические условия равновесия системы сходящихся сил на плоскости

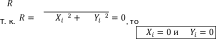
Известно, что силы взаимно уравновешиваются, если их равнодействующая равна 0, т. е. =0.

(2)

Т. е. для того, чтобы тело под действием плоской системы сходящихся сил находилось в равновесии, необходимо и достаточно, чтобы алгебраические суммы проекций сил системы на оси координат были равны нулю.

Уравнения (1) являются аналитическими условиями равновесия плоской системы сходящихся сил.

1.6. Общая методика решения задач на равновесие сил, приложенных к твердому телу (точке):

1. Выделяют твердое тело (точку), к которому приложена уравновешивающаяся система сил.

2. Показывают все действующие на тело активные (задаваемые) силы.

3. Согласно принципу освобождаемости от связей, действие связей на тело заменяют реакциями.

4. К полученной системе сил применяют условия равновесия, соответствующие этой системе.

5. Из условий равновесия определяют искомые величины.