5.3. Мгновенная угловая скорость и мгновенное угловое ускорение

Мгновенная угловая скорость сферического движения твердого тела – вектор, направленный вдоль мгновенной оси вращения, модуль которого равен

. (76)

Причем вектор мгновенной угловой скорости будет равен:

, (77)

где – вектора угловых скоростей вращения вокруг осей Oz (собственное вращение), Oz₁ (прецессия) и ОК (нутация) (см. рисунок 35), численно равные первым производным от соответствующих углов Эйлера повремени.

Векторная величина

, (78)

характеризующая изменение с течением времени угловой скорости и по модулю, и по направлению, называется угловым ускорением тела в данный момент времени или мгновенным угловым ускорением.

При изменении вектора его конец А будет описывать в пространстве некоторую кривую AА1, являющуюся годографом вектора (см. рисунок 37).

Сравнивая выражение (78) с равенством можно сделать вывод, что угловое ускорение тела можно находить как линейную скорость, с которой конец вектора перемещается вдоль кривой AА .

Направление вектора совпадает с направлением касательной к кривой AА₁ в соответствующей точке. Следовательно, в данном случае, в отличие от случая

вращения вокруг неподвижной оси, направление век- тора не совпадает с направлением . ^{Рисунок 37}

5.4. Скорости и ускорения точек тела, движущегося около неподвижной точки

На основании теоремы Эйлера – Даламбера, рассмотренной в п.5.2, скорость любой точки твердого тела, совершающего сферическое движение, можно определить как скорость при вращении точки вокруг мгновенной оси Р:

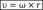, (79)

=

вращения ОР.

Таким образом, ускорение точки твердого тела при сферическом движении равно геометрической сумме вращательного и осестремительного ускорения.

Вектор направлен перпендикулярно плоскости, проходящей через точку М и вектор , а по модулю а₁ = ε·h₁, где h₁ – расстояние от точки М до вектора .

Вектор , перпендикулярный одновременно и , направлен вдоль МС, причем по модулю .

Модуль полного ускорения равен:

.

Следует отметить, что вектор не является вектором касательного ускорения точ-

ки М (по касательной направлен вектор , а направление вектора будет другим). Следовательно, и вектор не будет вектором нормального ускорения точки М.

Вопросы для самоконтроля

1. Какое движение точки называется сферическим? Приведите примеры.

2. Запишите уравнение сферического движения. Какие углы называются углами Эйлера?

3. Приведите формулировку и доказательство теоремы Эйлера – Даламбера. Какая ось называется мгновенной осью вращения?

4. Как определяются мгновенная угловая скорость и ускорение твердого тела при сферическом движении?

5. Чему равен вектор и модуль скорости точек твердого тела, движущегося около неподвижной точки?

6. Какие ускорения называются вращательным и осестремительным? Чему они равны? Как с их помощью найти вектор и модуль ускорения точек твердого тела, совершающего сферическое движение?