
Статика и кинематика / Статика
.pdfЛекция 6
1.Условия равновесия для частных случаев: системы параллельных сил в пространстве, произвольной плоской системы сил, системы параллельных сил на плоскости.
2.Различные формы условий равновесия произвольной плоской системы сил.
3.Решение задач статики.
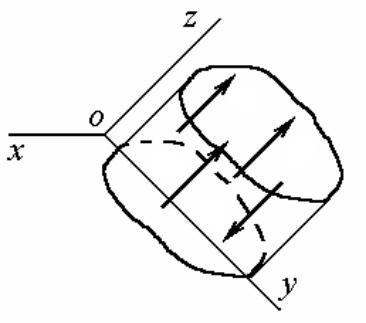
1.22. Частные случаи условий равновесия произвольной пространственной системы сил
Система параллельных сил в пространстве
|
|
|
|
|
|
|
|
|
N |
|
N |
N |
|||
|
|
|
|
|
|
|
|
|
Fkx 0, |
Fky 0, mz (Fk ) 0. |
|||||
|
|
|
|
|
|
|
|
|
k =1 |
k =1 |
k =1 |
||||
|
|
|
|
|
F1 |
|
|
|
|
N |
|
|
|
||
|
|
|
|
|
|
|
F2 |
|
|
Fkz |
= 0, |
|
|
||
F |
|
|
|
|
|
|
|||||||||
|
N |
|
|
|
|
|
|
|
k =1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fk |
|
|
|
|
N |
|
|
|
N |
|
|
||
|
|
|
|
|
|
|
|
|
mx (Fk ) = 0, |
my (Fk ) = 0. |
|||||
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
k =1 |
||
Для равновесия системы параллельных сил в пространстве необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную этим силам, равнялась нулю и чтобы сумма их
моментов относительно каждой из двух координатных осей, перпендикулярных силам, также равнялись нулю.
Система сходящихся сил
N |
N |
N |
||||||
|
|
|
|
|
|
|
|
|
mx (Fk ) 0, |
my (Fk ) 0, |
mz (Fk ) 0. |
||||||
k =1 |
k =1 |
k =1 |
||||||
N |
N |
N |
Fkx = 0, |
Fky = 0, |
Fkz = 0. |
k =1 |
k =1 |
k =1 |
Для равновесия пространственной системы сходящихся
сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех выбранных любым образом координатных осей равнялись нулю.
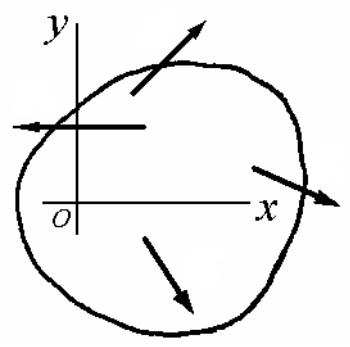
Произвольная плоская система сил
|
|
|
|
|
|
|
N |
N |
||
|
|
F1 |
||||||||
|
|
Fkz 0, |
mx (Fk ) 0, |
|||||||
|
|
|
|
|
|
|
||||
FN |
k =1 |
k =1 |
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
||
|
|
|
|
|
|
|
|
|
N |
N |
|
|
|
|
|
|
|
|
|
Fkx = 0, Fky = 0, |
|
|
|
|
|
Fk |
||||||
|
|
|
|
|
|
k =1 |
k =1 |
|||
N
my (Fk ) 0.
k =1
N
mO (Fk ) = 0.
k =1
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма
моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.
1.23. Различные формы условий равновесия произвольной плоской системы сил
N |
N |
N |
Fkx = 0, |
Fky = 0, |
mO (Fk ) = 0. |
k =1 |
k =1 |
k =1 |
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил, относительно любой точки, лежащей в плоскости действия сил, были равны нулю.
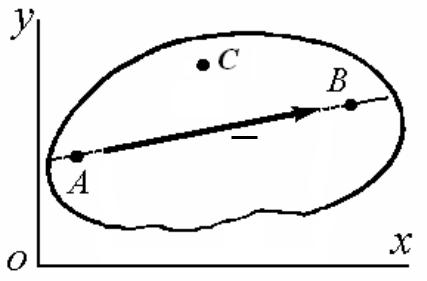
Вторая форма условий равновесия
(теорема о трех моментах)
R *
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой, были равны нулю, т.е.:
N |
N |
N |
||||||
|
|
|
|
|
|
|
|
|
mA (Fk ) = 0 |
mB (Fk ) = 0 |
mC (Fk ) = 0 |
||||||
k =1 |
k =1 |
k =1 |
||||||
|
|
|
||||||
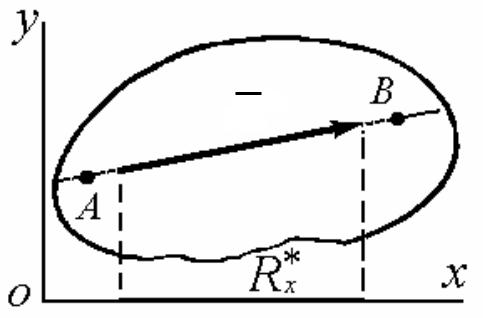
Третья форма условий равновесия
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно двух любых точек А и В и сумма их проекций на ось Оx, не перпендикулярную прямой, проходящей через точки А и В, были равны нулю:
N |
N |
N |
||||
|
|
|
|
|
|
|
mA (Fk ) = 0 |
mB (Fk ) = 0 |
Fkx = 0 |
||||
k =1 |
k =1 |
k =1 |
||||
|
||||||
R *
1.24.Решение задач статики
1.Сделать чертеж и выделить тело, равновесие которого надо рассмотреть в данной задаче.
2.Изобразить на чертеже активные силы.
3.Выбрать наиболее удобную систему координат. Отбросить связи и заменить их силами реакций.
4.Рассмотреть равновесие данного несвободного твердого тела как свободного, находящегося под действием активных сил и сил реакций. Для получившейся системы сил записать соответствующие условия равновесия.
5.Составить условие равновесия и решить получившуюся систему уравнений относительно искомых в задаче величин.
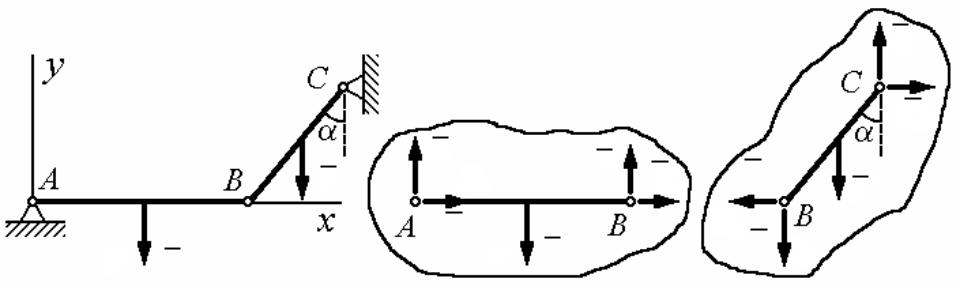
Пример 1.4. Две однородные одинаковые балки весом Р каждая соединены шарниром В и прикреплены шарнирами А и С к неподвижным опорам так, что балка АВ горизонтальна, а балка ВС образует с вертикалью угол. Определить реакцию шарниров.
YC
X C
P YA YB X B X B P
P X A P YB
Для балки АВ:
Для балки ВС:
N
Fkx k =1
N
Fky k =1
N |
|
|
|
|
|
|
|
Fkx = 0, |
X A+X B = 0. |
||||||
k =1 |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
Fky = 0, |
YA+ YB − P = 0. |
||||||
k =1 |
|
|
|
|
|
|
|
N |
|
|
|
|
l |
|
|
mA |
|
|
|
− P |
+YBl = 0. |
||
(Fk ) = 0, |
|||||||
|
|||||||
k =1 |
|
|
|
2 |
|
||
= 0, |
|
|
− X B +X C = 0. |
||||
= 0, |
|
|
YC −YB − P = 0. |
||||
|
|
N |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
− P |
sin +Y |
l sin − X |
|
l cos = 0. |
||||||
|
m (F |
) = 0, |
C |
||||||||||||
|
|
||||||||||||||
|
B k |
|
2 |
|
C |
|
|
|
|||||||
|
k =1 |
|
|
|
|
|
|
|
|
|
|
||||
X |
= − X |
|
= − X |
= − P tg , Y =Y = |
P |
, Y = |
3 |
P. |
|||||||
C |
|
|
|||||||||||||
A |
|
|
|
B |
|
|
|
A B |
2 |
C |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
