Добавил:

Punk0tta bettaalpha553@gmail.com Discord @punk0tta#0252 TG punk0tta Inst v_is_vsevolod Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет строительства и архитектуры

Предмет:

Сопротивление материалов

Файл:

BUDMECH.pdf

Скачиваний:

Добавлен:

21.05.2021

Размер:

26.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

О П А

11. Метод сил

Зміст глави

.	.	тупін статично неви начуваності
.	. Основна систе		а і основні невідо	і етоду сил
.	.	исте а ро в	увал ни рівн н	етоду сил
.	. О численн коефіцієнтів систе и канонічни рівн н
.	. Перевірка коефіцієнтів канонічни			рівн н


11.6. Ви наченн дійсни				усил
11.7. О численн пере і				ен	у статично неви начувани	систе	а
11.8. іне		атична перевірка ро ра унку
11.9. Приклад ро ра унку статично неви начувано ра и						етодо	сил
11.10. Використанн си етрі
11.10.1.		и етрі	ро ра унково с е и і навантаженн
11.10. .		авантаженн		а ал но о ви л ду
11.10. .		и етричне навантаженн
11.10. .		ососи	етричне навантаженн
11.10. .		рупові невідо		і
11.11.	о ра унок статично неви начувани фер
11.12. Приклад ро ра унку статично неви начувано фер						и
11.13.	о ра унок неро рі ни				алок
11.13. .		івн нн	тр о	о	ентів
11.13. .		етод	о ентни фокусів
11.13. . По удова о инаючи епюр
11.14. Осо ливості ро ра унку статично неви начувани						ко іновани систе

ето

11.1.

тупінь статичної невизначуваності

Основною

арактеристикою

статично

неви начувани

систе

ступін

статично

неви начуваності,

кий

арактери ує кіл кіст надлишкови ,

а о

айви

точки

ору

кіне атично о аналі у в

ей

ак, ра а,

о ражена на рис. .

,а,

ає дві жорстко атиснені опори і, отже, шіст

невідо

опорни

реакцій.

іншо о оку, ра

вл є со ою один диск, дл

ко о на пло

ині ожна скласти

три рівн нн рівнова и.

аки чино ,

дл ви наченн опорни реакцій не вистачає тр о рівн н .

і ниц

іж

кіл кістю

невідо и

статични

арактеристик

і кіл кістю

рівн н

рівнова и

арактери ує ступінь статичної невизначуваності стержнево систе и.

о у така ра

а становит

тричі статично неви начувану систе

у.

ис.11.1

а а

істит

одне

айве

атисненн , ліве а о праве, і в ц о у

айво у

атисненні

виникают

три

айві

опорні реакці . о

у кажут , о така ра

ає три

айві кіне

атичні в і

о просто

три

айві в

і.

тупін

статично

неви начуваності

оже ути о числений

а фор

улою

е ишова. Проте дл

практични

ро ра унків існує

ручніша фор ула

n=3k .

(11.1)

цій фор улі n

ступін

статично

неви начуваності плоско

стержнево

систе

и,

k число

кнени

контурів у с е і,

ке ви начаєт с

кіл кістю

діл нок, на кі ро поділ є

пло ину

ро ра ункова с е

а споруд,

кіл кіст

прости

шарнірів,

кі в од т

до

кнени

контурів.

ак, ра

а на рис.

. ,а

ає лише один

а кнений контур і не

істит

шарнірів. Отже

n = 3 1

0 = 3.

кладніша ра	а пока ана на	рис. . ,	. Вона ає три а	кнені контури, кі о ражено
штри ови и ліні	и, і сі прости	шарнірів	у шарнірно-неру о	и опора A і D та у ву лі F по

ето

одно у, в шарнірно-ру о ій опорі B

два прості шарніри. акож дво

прости

шарніра

є еквіва-

лентни складний шарнір у ву лі L. Отже, n = 3 3

, то то ра

істит

дві

айві

і і є

двічі статично неви начуваною.

Бувают

випадки,

коли

фор

улою

(11.1) скористатис

важко а о навіт

не

ожливо.

ак

представлена на рис.

. ,а ра

а,

істит

стержні EH та

FG,

кі не

єднуют с

іж со ою в точці

перетину, а

лише пере ре уют с .

Внаслідок відсутності

єднанн

виникає утрудненн

при

ви наченні кіл кості а

кнени контурів.

ис. .

тупен

статично

неви начуваності о начено

с е

ожна о числити

ідно

фор улою

. ійсно, ожна трактувати ро ра ункову с е

к сукупніст

дво дисків

ла

ано о стержн

AGHB і диска-основи

рис. . ,

иски

єднані

іж со ою тр о а кіне атични

и в

стержні EF, EH i FG , а також дво

а прости и шарніра

и A i B. Припайки та ву ли в

ей

відсутні.

о то

=2,

=0, П=0,

та

. Отже

3 2

4 .

ожна

астосувати

й такий

прийо .

точку пере ре енн

кіне

атични

ей у овно

вводит с

шарнір точка

на рис.

. ,в .

е до вол є ви начити кіл кіст

а кнени

контурів

k =

і кіл кіст

прости

шарнірів.

ц о

у випадку

по одно

у шарніру в точка

A,B,G,H; по

два прости

шарніри в точка E i F, а також потрійний шарнір в точці O).

аки

чино

фор

улою

11.1

ає

n 3k

3 5 11 4.

ето и

11.2.сновна система і основні невідомі методу сил

подал шо

ці

сили

ви начати

ут с

в першу чер у.

Вони

становл т

основні

невідо і

адачі

і по начают с

си вола и

X1, X2,

...,Xn, де

ступін

статично

неви начуваності

адачі.

ак,

на рис. .

о ражено кіл ка основни

систе

ра и

рис.

. ,а ,

кі одержано відкиданн

ти

чи інши

айви

ей. В усі випадка

утворені основні систе

ео етрично не

інювані і неру о і.

ожна навести кіл ка найпоширеніши

спосо ів відкиданн

айви

ей

Відкиданн

опорни

ей.

При

ц о

у до

основно

систе и

прикладают с

реакці

відкинути

ей

рис.

,а,

, .

Введенн

шарніра еквівалентне відкиданню одніє

і. При ц о у

о о

оків від

шарніра прикладают с

осереджені

енти невідо о

величини,

кі дорівнюют

один

одно

у, але спр

овані в протилежни

напр

рис.

,в,е .

о рі

стержн ,

кий

ає на о о

кінц

жорсткі ву ли, є еквівалентни

відкиданню

тр о

ей. При ц о

у в ісці ро рі у прикладают с

по довжні, поперечні сили, а

також осереджені

енти, величини

ки невідо

і рис.

. ,д .

ис.11.3

ето

11.3. истема розв’язувальних рівнянь методу сил

авд ки

пере оду

від

ро ра унково

с е и

до

основно

систе и

ро ра унок

статично

неви начувано

с е и

інюєт с

на

ро ра унок

статично ви начувано основно

систе

и.

ефор аці і, отже, усилл ,

кі виникают

у ци дво с е

а ,

удут

рі ни

и.

усуненн

ро

іжності в дефор

уванні ци

дво

с е

на основну систе

у слід накласти

додаткові у

ови,

кі

ро л т

не

ожливи

и пере

і енн

в напр

і відкинути

айви

ей.

і у ови

ожут

ути одержані

е посередн о і

ро

л ду дефор

ацій основно систе и від

адани

овнішні

дій та від ді основни

невідо и .

Повне пере

енн

основно систе

и в напр

айво

оже

ути представлене

су а пере і

ен

окре

о від ді кожно о

айво о невідо

о о і

овнішн о о навантаженн .

ак, дл

двічі статично неви начувано

ра и рис.

. ,а , основна систе

ко

пока ана на рис.

ис.11.4

ето

1P ;

2P ,

де

пере

енн

в стані k основно

систе

и в напр

і основно о невідо о о

Xi .

ожне

пере

ен ,

овлене дією

айво о невідо о о

рис.

. ,в,

, оже

ути представлене к до уток

пере

енн

від

ді

ц о о

невідо о о,

ке у

овно

прий

аєт с

а одиницю, на

йо о

дійсну

невідо

у величину

11 11 X1 ,

12 X 2 ,

21 X1,

22 X 2 ,

де ik

анало ічні

пере

і енн

від

ді

айви

одинични

невідо

и .

Величини

арактери уют

пере і

енн

основно

систе

напр

і основно о

невідо

о о

Xi у

вантажно у стані

рис.

. ,д).

Вра овуючи,

о дійсні

пере і

енн

адано

ра

и в

напр

айви

ей відсутні

(рис.

. ,е , то то 1

рештою оже

о аписати

11 X1	12 X 2	1P
21 X1	22 X 2	2P

л	n ра ів статично неви начувано систе и повне пере і енн в напр і відкинуто айво
в і	оже ути аписане анало ічно

= i1+

i2+ ... + ii + ... + in+

ip = 0,

(11.2)

але

i1 X1 ,

i2 X 2

, , ii

ii X i , ,

in X n .

(11.3)

Підставивши

. у

, дістане

о рівн нн

i1 X1

i2 X 2

ii X i

in X n

ip 0.

(11.4)

аписавши рівн нн

послідовно дл

кожно

відкинуто

і, до оди о систе

и рівн н

відносно основни

невідо и

адач

11X1

12 X2

1n Xn

21X1

22 X2

2n Xn

2 p

(11.5)

n1X1

n2 X2

nn Xn

ето и

истема лінійних алгебраїчних рівнянь (11.5 є математичною умовою відсутності

переміщень в основній системі в напрямах відкинутих зайвих в’язей. При виконанні цих умов деформований і, отже, й напружений стан статично визначуваної основної системи буде еквівалентним напружено-деформованому стану вихідної статично невизначуваної системи.

івн нн

11.5

не

алежат

від ви л ду, навантаженн , о рано

основно

систе

и,

чи від

арактеру основни

невідо

и . Вони

ают

стандартний

канонічний ви л д

кіл кіст

рівн н

і,

отже,

кіл кіст

невідо

кожно

рівн нні,

дорівнює ступеню

статично неви начуваності n;

коефіцієнт ij при кожно

у невідо

ає два індекси перший індекс i відповідає но

еру

р дка, дру ий індекс j

но еру стовпц

но

еру невідо

о о

у кожно

у рівн нні є віл ний член

ip, перший індекс

ко о відповідає но еру рівн нн

коефіцієнти ii, ро ташовані на

оловній

діа оналі

систе

рівн н ,

суттєво додатні

на ивают

оловни

и коефіцієнта

по ічні коефіцієнти відповідно до теоре

аксвелла

ij= ji

си

етричні відносно оловно

діа оналі систе

и рівн н

исте

а рівн н

на иваєт с

евідо і

систе

и канонічни

рівн н

становл т

сили

реакці

відкинути

айви

ей, коефіцієнти

пере

енн

в основній систе

і в напр

і ци

ей від ді

одинични

основни

невідо

и .

оефіцієнти при невідо

на ивают

одиничними пере

і енн

и, а віл ні члени

вантаж-

ними.

ідно

о начени

и правила

ожна

аписувати систе

у рівн н

етоду сил фор

ал но.

ак,

дл

ра

рис. .

ка

ає три

айві

і,

систе

а канонічни

рівн н

етоду сил

ати е

ви л д

11 X1	12 X 2	13 X 3	1p
21 X1	22 X 2	23 X 3	2 p
31 X1	32 X 2	33 X 3	3 p

0;	(11.6)
0.

	ео ідно вра овувати те,		о конкретний фі ичний				іст рівн н	інюєт с		алежно від
ви ору основно систе и і при наченн					основни	невідо	и . ак, к о перше рівн нн				.
дл	основно систе и рис.	.	,а	виражає відсутніст ори онтал но о пере				і	енн	перері у B, то
дл	дру о основно систе и рис.			. , )	рівніст	нулю вертикал но о пере і			енн	перері у A, а
дл	основно систе и рис.	. ,е)		рівніст нулю кута повороту на опорі B.

ето

исте

а канонічни

рівн н

етоду сил

оже

ути

аписана в

атрично

у ви л ді

B X

(11.7)

де

вектор основни

невідо

и ,

вектор вантажни

пере

ен ,

атриц

податливості основно

систе

и в напр

відкинути

ей

(11.8)

n2 nn

а адає

о властивості еле ентів

атриці податливості

оловні коефіцієнти – додатні числа

ii > 0;

по ічні коефіцієнти є си етрични

и відносно

оловно

діа оналі, то то ij = ji.

л ви наченн

систе

и канонічни

рівн н

етоду сил

ожна скористатис інши

під одо ,

а уєт с

на теоре

астіл

но

, точніше на окре

випадку,

ідно

ки

частинні

по ідні від потенціал но

енер і

дефор

аці

по реакці

" айви " в

ей систе

и дорівнюют

нулю теоре

ена реа .

Потенціал на

енер і дефор

ацій при ура уванні тіл ки

инал ни

ентів виражаєт с

співвідношенн

M 2

dx.

(11.9)

0 2EI

еруючис

принципо

не алежності дій,

инал ний

ент у довіл но у перері і

уд -

ко о

стержн

основно

систе

и n ра

статично

неви начувано

ро ра унково

с е

оже

ути

виражений чере

прикладені сили

1 X1

M p ,

M M

M 2 X 2

M i X i

M n X n

(11.10)

де

i ( x ), M p

M p ( x )

функці

координати

x перері у стержн ,

кі виражают

инал ні

енти в основній систе

і,

овлені дією основни

невідо

и Xi = 1 (i = 1,2,...,n) і

адано о

овнішн о о навантаженн

відповідно.

ето

ео ідною у

овою екстре

у у функціонала потенціал но енер і

є рівніст

нулю першо о

диференціала, о еквівалентно рівності нулю всі

перши

по ідни

по не алежни пара етра

навантаженн

X1, X2, ..., Xn.

накше кажучи, повинна

ати

ісце рівніст

(11.11)

X i

2EI

к відо о, по ідну

ожна внести під

нак інте рала

M 2

dx 0.

X i

2EI

Виконає

о диференціюванн , вважаючи жорсткості стержнів EI постійни и

(11.12)

X i

По ідна від

инал но о

енту 11.10

ає ви л д

M1 X1

M 2 X 2

M i X i

M n X n M p

M i .

X i

Підставивши по ідну до .

	U	X1

	X i
	X i
		X n

, одержи о

l				i				1	dx X 2
		M				M
0			EI


l			i				n
	M				M				dx
0		EI

	l				i			2	dx
	l		M		i	M		2

	0			EI
	0
l		i M p
l	M	i M p					dx 0.
0	EI						dx 0.
	EI

Беручи до ува и те,

о вира и при невідо

і віл ний член вл ют

со ою пере і

енн ,

апише

i1 X1

i2 X 2

in X n

0 ,

то то

одержи

о ре ул тат,

анало ічни

11.4 .

О начене рівн нн виражає

у ову

неро ривності

дефор аці

в напр

айво

відкинуто

в і.

иференціюючи

потенціал ну

енер ію U почер ово по кожно

у пара етру Xi

(i = 1,2,

... , n ,

одержи

о систе

у канонічни

рівн н

11.5).

ето и

11.4.бчислення коефіцієнтів системи канонічних рівнянь

оефіцієнти систе и канонічни				рівн н		етоду сил еле	енти	атриці податливості основно
систе и	вл ют	со ою	пере і	енн	основно систе и		від	ді	основни невідо	и ,	кі
покладают	а одиницю. л		о численн		нео	ідно скористатис фор			улою аксвелла–	ора,	ка
дл плоски	систе	ає ви л д

i N p

i M p

QiQp

dx.

рі но о типу ро ра ункови

с е

вичайно утри

уют

лише де кі складові фор

ули. ак,

при ро ра унку еле

ентів,

кі переважно працюют на

ин

алки, ра и , утри уєт с

доданок,

кий

алежит

від

инал ни

о ентів

i M p

dx,

dx.

(11.13)

фер

ура овуют лише по довжні сили

i N p

dx,

dx.

(11.14)

л арок

i N p

		i		j
	M	i	M	j	dx,	(11.15)

l	EI
	EI

M i M p dx. EI

аки

чино ,

дл

о численн

коефіцієнтів систе

канонічни

рівн н

нео

ідно

ви начити

усилл ,

кі виникают

всі

еле ента

основно

систе

и від ді

овнішн о о

навантаженн , а також від ді кожно о основно о невідо о о Xi = 1.

практични

ро ра унка

е посереднє інте руванн

інюєт с

чисел ни

використанн

правила Вере а іна,

фор

ули

псона –

орноу ова,

фор

ули пр

окутників,

трапецій то о.

о у дл

подал шо о ро ра унку

удуют с епюри

усил

у статично ви начуваній основній

систе і.

ак, дл

ра

и, о ражено

на рис.

. ,a, при використанні

основно

систе и

рис.

. ,а

по удовано

епюри

1 ,

2 ,

від ді

одинични

основни

невідо

і епюра

M p

від ді

овнішн о о навантаженн

рис. .

, післ

чо о а фор

ула

11.13

ожна о числити

коефі-

цієнти канонічни

рівн н

11.6).

ето и

ис. .
о в ок систе и рівн н ви начає величини основни невідо и	реакцій айви в ей.

11.5. Перевірка коефіцієнтів канонічних рівнянь

Правил ніст

остаточни

ре ул татів

ро ра унку

алежит від то о, наскіл ки правил но

о числено коефіцієнти систе

и ро в

увал ни рівн н . По и ки у коефіцієнта

овлюют

и ні а о неточні ре ул тати ро в

анн

канонічни

рівн н , то то по

илки у величина

реакцій

відкинути

ей і, внаслідок ц о о,

неправил ні

усилл

у ви ідній статично неви начуваній

систе і. Причо у на

ре ул тати най іл ше

впливают

по и ки

оловни коефіцієнта ii ,

ро ташовани

на

оловній діа оналі

атриці податливості (11.8),

і у

еншій

ірі – по и ки у

по ічни та вантажни

коефіцієнта .

Перевірки

а уют с

на, так ваній, су

арній одиничній епюрі

инал ни

о ентів,

ка

вл є

со ою епюру

инал ни

ентів

MS ,

по удовану в основній систе

і від одночасно

ді

всі

основни

невідо

и ,

кі вважают с

таки и,

о дорівнюют

одиниці.

ак дл

основно

систе и,

представлено на рис.

, , су арна одинична епюра пока ана на рис.

,д.

а начена

епюра

оже

ути по удована спосо о

накладенн

епюр,

кий

а уєт с

на

принципі не алежності ді сил

M1 M2 M3 .

л n ра ів статично неви начувано

систе

Mn .

(11.16)

ето

По

ножи о

а фор улою

ора су

арну одиничну епюру

инал ни

ентів MS

на

уд -

ку одиничну епюру Mi :

l MiMS dx

l Mi M1 M2 Mn dx .

відси

ожна

аписати:

l MiMS dx

l MiM1 dx

l MiM2

l MiMn dx

а о

MiMS dx

ij.

(11.17)

j 1

аки

чино

дл

перевірки о числен

достатн о

а фор

улою

ора по

ножити

уд - ку

одиничну епюру Mi

на су

арну одиничну епюру MS

і ре ул тат порівн ти

су ою коефіцієнтів

р дка

атриці податливості.

ака перевірка на иваєт с

р дковою.

нео

ідно виконати дл

кожно о р дка

атриці податливості.

той

са ий

спосі

ожна

пока ати,

ноженн

епюри

са

на се е

повинна

дорівнювати су

і всі

еле ентів

атриці податливості

MS MS dx

(11.18)

1 j 1

о то

а іст

ноженн

кожно одинично

епюри

ожна по

ножити са

у на се е су

арну

одиничну епюру

і порівн ти ре ул тат і

су

ою всі

еле

ентів

атриці податливості.

ака

перевірка на иваєт с

універсал ною.

Анало ічно перевір ют с вантажні пере

енн :

MS M P dx

iP.

(11.19)

i 1

Отже, дл перевірки нео

ідно пере

ножити су

арну одиничну епюру MS на вантажну епюру

MP і порівн ти ре ул тат і

су

ою всі

вантажни

пере

ен .

ето

11.6. Визначення дійсних зусиль

снує два основні спосо и ви наченн

дійсни

усил

в еле

ента

статично неви начувано

систе

и,

о ро ра овуєт с

етодо

сил. О идва спосо и

рунтуют с на то

у,

о епюри

фактично

удуют с

не в

аданій с е

і, а в статично ви начуваній основній систе

і,

ка пере уває

під

дією

адани

овнішні

навантажен

реакцій

відкинути

ей,

кі

найдено

післ

ро в

анн

канонічни

рівн н .

Перший спосі ,

кий

на ивают

статичним,

пол

ає

то

у,

виконуєт с

вичайний

статичний ро ра унок основно

систе и

від

одночасно

ді

всі

сил,

включно

основни

невідо

и и адачі.

При ц о

вичайни

и спосо а и ви начают с

опорні реакці

удуют с

епюри

усил , а о відшукуют с

ні величини в арактерни точка

с е

и.

ру ий

спосі

це

спосі

накладання.

Він

рунтуєт с

на

принципі не алежності дій

принцип суперпо иці

і пол

ає в то

у,

о уд - ке усилл , напруженн

а о пере

енн

оже

ути одержане к су

а ци

величин від кожно ді окре

о.

а цій підставі

ожна

аписати

1 X1

2 X 2

n X n

M p ;

Qp ;

(11.20)

Q1 X1

Q2 X 2

Qn X n

2 X 2

n X n

N p .

N1 X1

Під величина

слід ро у

іти а о

усилл в

ко

ус

перері і а о епюри

усил

i ,Qi ,

основній систе і,

овлені дією одинични

основни невідо

рис. . ).

ійсні епюри

усил

у ра і,

о ро л даєт с ,

по удовані на рис.

,а,

,в.

При ц о

іж

епюра

и M i Q виконуєт с

диференціал на алежніст

Q = dM / dx.

практични

ро ра унка

ожна дійсну епюру

инал ни

о ентів M

удувати

а спосо о

накладенн

M M1X1 M2 X2 Mn Xn M ,

поперечні сили одержати на

а і диференціал но

алежності Q

dM / dx,

а по довжні сили –

шл

аналі у

рівнова и

ву лів

а о

фра

ентів

с е

и, до

ки

прикладено

овнішні

навантаженн та

найдені

инал ні

о енти та поперечні сили в перері і,

ки

виділено ву ол чи

фра

ент.

ето и

ис.11.6

11.7. бчислення переміщень у статично невизначуваних системах

Пере і

енн

статично

неви начувани

систе а

ожут

ути

о числені

а фор

улою

аксвелла–

ора

k N

k M

Qk Q

dx.

(11.21)

ц о

у співвідношенні

M ,Q , N

дійсні

усилл

статично

неви начуваній

систе

і,

k ,

усилл ,

овлені одиничною у а ал неною силою,

о відповідає шукано

Qk ,

пере

і енню. О начені

усилл

ожут

ути о числені дл

ви ідно

статично неви начувано

систе

и.

ц о о

доведет с

ро ра овувати а

етодо

сил на дію допо

іжно о одинично о

навантаженн .

Проте

ти

до

ува и,

дійсні

усилл

M ,Q , N

фактично

о числюют с

в статично ви начуваній основній систе і,

то пере і

енн також

ожут

ути

о числені в тій са

ій основній систе і.

Отже,

усилл

k ,

ожна

найти в статично

Qk ,

ви начуваній основній систе

і,

ка пере уває під дією

овнішні навантажен

і дійсни

величин

реакцій у відкинути

Біл ше то о, оскіл ки кінцеві

наченн

дійсни

усил

не

алежат

від ви ору основно

систе

и, дл о численн

пере

ен

ожна

рати

к основну систе

у,

кою

провадивс

ро ра унок,

так

уд - ку іншу.

ак,

дл

ви наченн

ори онтал но о

пере

і енн

ри ел

в ра

і,

о ро

л даєт с ,

ожна прикласти до ри ел

в допо іжно

у стані

ето

одиничну

ори онтал ну силу і по удувати одиничну епюру

в основній систе і,

кою

провадивс

ро ра унок рис.

,а ,

а о в уд - кій іншій, наприклад,

в основній систе і,

о ражена на рис.

. ,в. Відповідна одинична епюра пока ана на рис.

. , .

Отже,

ви наченн

пере

енн

в статично неви начуваній систе

і від ді овнішн о о

навантаженн слід виконувати в такій послідовності

Ви начити дійсні

усилл

в статично неви начуваній систе і M

,Q , N ).

Ви рати уд -

ку основну систе

у етоду дл

ви ідно статично неви начувано систе

и.

творити допо іжний "одиничний"

стан

k ціє

основно систе

и, приклавши

до

не

одиничну у а ал нену силу,

о відповідає шукано

у пере і енню.

Ви начити усилл

в допо

іжно

уодинично

у стані

k ,

Qk ,

k ).

О числити пере і

енн

а фор

улою

аксвелла–

ора 11.21).

11.8. Кінематична перевірка розрахунку

перевірки

правил ності

ро ра унку

уд - ко

статично

неви начувано

систе и

астосовуют

так

вану кінематичну перевірку. Вона пол

ає в о численні пере і

енн ,

ке

напевне

дорівнює

нулю.

аки и

пере і енн

и у ви ідній статично ви начуваній с е і є

пере і

енн

в напр а

існуючи

в ей. Пере

ножи о, наприклад,

а фор

улою

ора дійсну

епюру

усил

M ,

о по удована

а фор улою

11.20 , в n ра статично неви начуваній ра

і на

уд - ку одиничну епюру

i :

i M

1 X1

2 X 2

n X n

M p

dx.

о кривши дужки, а іни о інте рал су и на су у інте ралів. При ц о у винесе о постійні величини а наки інте ралів

i M

dx X1

dx X 2

i M n

X n

l Mi M 2 dx
0	EI

lMi M p dx. EI

ето

ра овуючи,

коефіцієнти

при

основни

невідо

вл ют

со ою пере

і енн ,

перепише

о одержаний вира

i M

i1 X1

i2 X 2

in X n

ip .

Порівнюючи праву частину співвідношенн

11.4), до оди

о висновку,

i M

(11.22)

аки

чино ,

дл

перевірки

правил ності

ро ра унку

статично

неви начувано

систе и

достатн о в уд -

кій основній систе і етоду сил ви начити

усилл від ді

уд - ко о основно о

невідо о о Xi = 1 і по ножити

а фор

улою

ора на дійсні

усилл .

о ре ул тат дорівнює

нулю, то

усилл

найдено правил но.

11.9. Приклад розрахунку статично невизначуваної рами методом сил

о ра ує о ра

у,

о ражену на рис.

. ,а

етодо

сил.

ис.11.7

а а

ає

два

кнені

контури

чотири

прості

шарніри,

то у

ступін

статично

неви начуваності

3 2

аки

чино ,

адана ра

ає дві

айві

і.

татично

ви начувану основну систе у

дістане

ра унок

н о о

відкиданн ,

наприклад,

введенн

дво

прости

шарнірів

рис. .

еакці

відкинути

ей,

то то

инал ні

енти

X1 i

X2 у перері а

стержнів,

ето	и	17
становити	ут основні невідо і етоду сил. исте а канонічни рівн н	етоду сил на уде
ви л ду

11X1	12 X2	1P
21X1	22 X2	2P

уло

а начено, ці рівн нн

є у

ова

и відсутності пере і

ен у напр

айви

в ей

і, отже, у ова

и неро ривності дефор

ацій.

оефіцієнти при основни невідо

и і віл ні члени

арактери уют

пере

енн

основній систе і

напр а

відкинути

ей.

н о о

о численн

по удує

епюри

внутрішні

усил

основній систе і окре о

від

ді

кожно о

невідо

о о,

ке

ерет с

а одиницю, а також від ді

овнішн о о навантаженн .

рис. . .

ис.11.8

ето	и	18
О числи	о коефіцієнти а допо о ою фор ули	ора.

l		M12								dx				1					1		3,6 1						2	1 2				1 1						1 6		2	1
										dx											3,6 1							1 2										1 6			1
0			EI											EI				2									3						2EI				2			3
1						1				1 4,8						2		1					4,2				;
										1 4,8					3			1						EI			;
2EI 2															3									EI
l																		1 1										1				1 1										2				0,3
l			M						M									1 1										1				1 1										2				0,3
	1 2											dx													1 6					1								1 4,8						1				;
0												dx					2EI					2			1 6			3		1				2EI			2	1 4,8				3		1			EI	;
0					EI												2EI					2						3						2EI			2					3					EI
l							22				dx				1 1												2					1 1								2				1,8
l				M			22								1 1							1 6					2	1				1 1					1 4,8			2		1		1,8		;
																						1 6						1									1 4,8					1				;
0				EI										2EI				2									3					2EI			2					3					EI
l																		4,8											1										1		1						1		2,088		;
l				M1M P								dx						4,8							0		4		1		8,64				0				1		1		12 6				1		2,088
					EI							dx			6					2EI					0		4	2			8,64				0				2EI		2		12 6			2
0					EI										6					2EI								2											2EI		2					2			EI
0
l								2M P					dx							1						1					1				4,8								1							15,912		.
l					M			2M P												1						1	12	6			1				4,8			0		4			1	8,64		0				15,912
																				2EI 2							12	6			2 6					2EI		0		4		2		8,64		0
0							EI													2EI 2											2 6					2EI						2								EI
0

ис.11.9

лперевірки правил ності о численн коефіцієнтів по удує о су арну одиничну епюру

инал ни	о ентів від одночасно ді всі	основни невідо и , кі	дорівнюют	одиниці
рис. . .	у ж са у епюру ожна по удувати	к су у одинични епюр	инал ни	о ентів
(рис. . ,	,е):

M1 M2 .

Перевірка пол ає в почер ово у пере

ноженні су арно одинично епюри

на кожну

одиничну

1 ,

і на вантажну M P епюри, по удовані в основній систе і, і в порівн нні

одержани

ре ул татів

су а и коефіцієнтів відповідни стовпців атриці коефіцієнтів

ето

MiM

1,2, ,n ;

j=1

M P M

jP .

j=1

рештою

ає

1 1

3,9

1 3,6

1 2

1 6 1

;

EI 2

2EI

4,2

0,3

3,9

21;

1,5

1 6 1

;

2EI

0,3

1,8

1,5

21;

M P

12 6 1

;

2EI

2,088

15,912

P .

одержани

ре ул татів

ожна дійти висновку,

о пере

і енн

основно систе и о числені

правил но. Підставивши коефіцієнти до систе

и канонічни

рівн н

і скоротивши на постійний

ножник EI ,

ає о систе

у лінійни ал е ра чни

рівн н

4,2X1 0,3X

0,3X1 1,8X

2,088 0;

15,912 0,

ро в ок ко ви начає величини реакцій у відкинути в

X1 1,142; X 2 9,030.

л ви наченн внутрішні		усил у	аданій ра і ожна	скористатис принципо
суперпо иці . ак, дійсні	инал ні	о енти	ожут ути о числені	к су а инал ни о ентів
в основній систе і від ді	кожно о чинника окре о


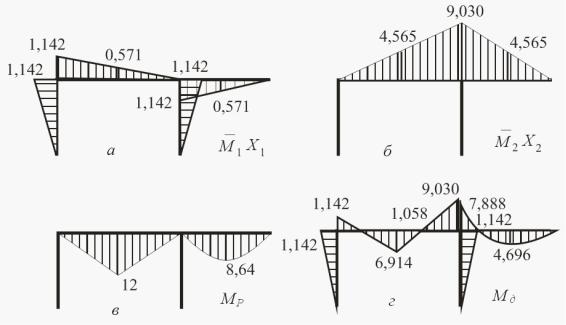
ето и	20
		n
M				i Xi M P .
			M
		i 1
л двічі статично неви начувано ра	и
M		1 X1				2 X 2 M P .
	M				M
По удову дійсно епюри инал ни	о ентів пока ано на рис. . .

ис.11.10

виконанн

кіне

атично

перевірки див.п.11.8

дійсно епюри

инал ни

ентів

рис.

слід пере

ножити

на

уд -

ку одиничну епюру

ентів,

по удовану в

уд -

кій

основній

систе

і.

ц о

у прикладі дл

перевірки

використає

су

арну одиничну епюру

инал ни

ентів

(рис.

. , ):

1 2

1,142 3,6

1 3 2,886

2EI

1 3 1,058

2,741 4,329

1,587

4,328

4,329

0 .

2EI

Отже, дійсна епюра инал ни	о	ентів відповідає у ова неро ривності дефор ацій.
ійсні епюри поперечни рис.	.	,а і по довжні сил рис. . , також ожна по удувати
а принципо суперпо иці

ето и

Q Q1X1 Q2 X2 QP ;

N N1X1 N2 X2 NP .

			ис.11.11
с ра	а	а ало , а також уд - кий	еле ент	ают пере увати	у стані рівнова и.
Перевіри о, наприклад, рівнова у одно о			ву лів.	л ц о о виокре лює о цей ву ол а
допо о ою	а	кнено о перері у і в перетина	прикладе	о внутрішні усилл	к вже відо і сили
рис. . .

ис.11.12

кладає о рівн нн рівнова и вирі ано о ву ла

M	9,030 1,142	7,888	0;
Fx	0,317 0,317	0;
Fy	5,315 8,843	14,158	0.

Отже, ро л нутий ву ол пере уває в стані рівнова и. Анало ічно ожна перевірити рівнова у уд - ко о еле ента а о всіє ра и.

ето	и				22
11.10. Використання симетрії
11.10.1.	иметрія розрахунково схеми і навантаження
исте	а на иваєт с симетричною відносно осі, к о		а допо	о ою пр о ,	котра і аєт с
віссю си	етрі ,	ожна ро ділити на дві частини, кожна	ки	є д еркал ни	відо раженн
іншо рис. .		,а .

ис.11.13

а о

си

етрични

и існуют

не цілко

си

етричні систе

и,

кі

ожут

ро л датис

си

етричні

а певни

ов.

ак, наприклад, ра

рис. .

оча і не повністю си

етрична,

оскіл ки

ає ліворуч шарнірно-неру о у,

праворуч

шарнірно-ру о

опору, при

ді

вертикал но о навантаженн

оже ро л датис

к си

етрична,

то

о ори онтал на реакці

ліво опори дорівнює нулю і дана опора

оже трактуватис

к шарнірно-ру о

а.

исте

и тако о

типу на ивают

умовно симетричними.

Пон тт

си

етрі

поширюєт с

на

навантаженн , дію

те

ператури,

енн

опор

ді

вважаєт с си етричною, к

о вона на одній половині конструкці є д еркал ни

відо раженн

ді

на дру ій половині

рис.

. ,в .

о ж ді

ро ташована си

етрично, але по відношенню до

осі

си

етрі

протилежни

напр

а ,

то така

ді

вет с

кососиметричною а о обернено-

симетричною рис. .

, .

окре а,

осереджена сила P, ліні

ді

ко

і аєт с

віссю си етрі ,

ето

є си

етричною,

а осереджена сила а о ро поділене навантаженн ,

кі прикладені до осі си етрі

напр

лені перпендикул рно до не ,

є кососи

етрични

и.

е са

ожна стверджувати відносно

осереджено о

о енту

рис. .

,д .

е пов

ано

ти

, о

осереджену силу P

ожна подати

дві осереджені сили величиною P/ , ро поділене навантаженн

інтенсивністю q

к два наванта-

женн

інтенсивністю q/

кожне, а осереджений

ент M

а інити парою сил рис. .

,е).

Буд - ка ді

а ал но о ви л ду

оже

ути представлена

к су а дво

дій,

одна

ки

си етричною, а дру а

кососиметричною а о оберненосиметричною.

априклад,

осереджена

сила P1 рис. .

,а

а інюєт с

дво

а си

етрични

и і дво

а кососи етрични и

осереджени

сила

и P1

, рівно

ірно ро поділене навантаженн

дво

а си

етрични

рис.

і дво

кососи етрични

и рис. . ,в

навантаженн

інтенсивністю

q/ .

о ді

початково

си етричною сила P2 а о кососи етричною, то ро кладенн

не

дійснюєт с .

							ис.11.14
а си етричне і кососи етричне					оже		ути ро кладене навантаженн ,				ке прикладаєт с в
си етрични	перері а ,	але	ає	рі ні		величини. ак,		два	осереджени		о енти M1 i M2
рис. . ,а	а інюют с	дво а		пара		и	осереджени	о	ентів.	о	енти першо пари
дорівнюют	M1 M2	2	рис.	.	,	і спр овані си		етрично.

ис.11.15

Величини о ентів дру о пари, кі спр овані кососи етрично, становл т (M1 M2)/2

рис. . ,в . При ц о у первісно кососи етрична сила P не ро кладаєт с .

ето и

11.10.2. авантаження загального вигляду

л		спро	енн ро ра унку а	етодо	сил си етрично систе и нео			ідно,	о	основна
систе	а	ула си етричною а о у		овно си	етричною.	акож нео ідно,	о	у ова	си	етрі та
косо си		етрі	відповідали основні невідо і.
о	л не		о, наприклад, ра у під дією навантаженн			а ал но о ви л ду	рис. .		,а .

ис. .

тупін

статично

неви начуваності n=3k

3 2

. Основну систе

у, одержану а

ра унок ро рі анн

ра

и по осі си

етрі ,

о ражено на рис.

, .

о основно систе

и прикладают с

основні невідо і,

вл ют

со ою усилл

ісц

ро рі ів. авд ки ро ташуванню на осі си

етрі

ра и основні невідо

і поділ ют с

на си

етричні

(X1, X2

і X4

та кососи етричні

і X5

навантаженн

на си

етричну основну систе

у.

ви наченн

основни

невідо

нео

ідно скласти і ро в

ати систе

у ро в

увал ни

канонічни

рівн н

етоду

сил,

ви л д

ко

алежит

лише

від

ступен

статично

неви начуваності ра и. Отже, ц систе

а канонічни

рівн н

оже

ути

аписана фор ал но

ето и

11X1	21X2	13 X3	14 X4	15 X5	1P
21X1	22 X2	23 X3	24 X4	25 X5	2P
31X1	32 X2	33 X3	34 X4	35 X5	3P
41X1	42 X2	43 X3	44 X4	45 X5	4P
51X1	52 X2	53 X3	54 X4	55 X5	5P

Епюри

инал ни

ентів

від

кожно о

основно о

невідо

о о

від

овнішн о о

навантаженн

по удовано на рис.

,в

, .

ачи

о,

у си

етричній основній систе і

епюри

инал ни

ентів

4 ,

овлені дією си

етрични

невідо и ,

є си-

M1,

етрични

и,

епюри

5 ,

по удовані

від

ді

кососи

етрични

невідо

кососи етрични и, а вантажна епюра

епюрою

а ал но о

ви л ду,

оскіл ки

вона є

ре ул тато

ді навантаженн

а ал но о ви л ду.

При

о численні

коефіцієнтів

систе и

рівн н

ле ко

впевнитис

то

у,

до уток

си етрични

епюр

на

кососи

етричні

тотожно

дорівнює

нулю.

е є природни , оскіл ки

очевидно,

о в си етричній систе і

си

етричні

ді

не

ожут викликати кососи

етричні

дефор аці

і навпаки. відси випливає,

0 .

рештою,

ви ідна

систе

т о

канонічни

рівн н

ро падет с

на дві не алежні

підсисте

и. Перша підсисте

істит

к невідо

і лише си

етричні сили

11X1	12 X2	14 X4	1P
12 X1	22 X2	24 X4	2P
14 X1	42 X2	24 X4	4P

а дру а лише кососи етричні сили, а са е

35 X3	53 X5	3 p
35 X3	55 X5	5 p

Підсисте и ро в уют с не алежно одна від одно . ійсні епюри ожут ути по удовані спосо о накладанн

ето и

1X1

2 X 2

3 X3

4 X 4

5 X5

M p ;

Q1X1 Q2 X 2 Q3 X3 Q4 X 4 Q5 X5 Qp ;

2 X 2

3 X3

4 X 4

5 X5

N p .

N1X1

ійсні

епюри,

кі

ре ул тато

накладанн

си етрични

кососи етрични

рафіків,

ати ут

а ал ний ви л д.

11.10.3.

иметричне навантаження

о л не о ту

са у статично неви начувану

ра у під дією си

етрично о

навантаженн

рис. . ,а . л

ро ра унку використає

о основну систе

у і основні невідо і, ви рані в попе-

редн о у пункті

рис.

, .

Очевидно,

ц о у випадку одиничні епюри

инал ни

о ентів

рис. .

,в

,ж

алишат с

ін і

систе

канонічни

рівн н також

ро падет с

на дві не алежні підсисте и.

Перша підсисте

а,

істит

к невідо

і лише си етричні сили

11X1	12 X2	14 X4	1P
12 X1	22 X2	24 X4	2P
14 X1	42 X2	24 X4	4P

інит	лише величини віл ни членів чере від інніст вантажно епюри инал ни о ентів
рис.	. ,в .

					ис.11.17
Внаслідок		си	етрі	епюри инал ни	о ентів вантажно о	стану віл ні члени дру о
підсисте	и,	о	істит	лише кососи етричні невідо і, дорівнюют		нулю. Отже, дру а підсисте а
рівн н	ає ви л д

ето

35 X3

53 X5

35 X3

55 X5

Отри

ана однорідна систе

а рівн н

при не виродженій

атриці

ає тривіал ний ро в'

ок.

атриц

коефіцієнтів

систе

канонічни

рівн н

не

вироджена авд ки

ео

етричній

не інюваності основно

систе

відси

ає

о X3 = X5 = 0.

Отже,

ожна

ро ити висновок,

ео

ідно

ви начати лише си етричні основні невідо

і.

ійсні епюри M і N

удут си

етрични

и, а

епюра Q

кососи

етричною.

11.10.4. Кососиметричне навантаження

о	л не о	е	ра ту	са у	статично	неви начувану		ра у рис. . ,а під дією
кососи	етрично о навантаженн			рис.	. ,а .	л	ро ра унку використає		о основну систе у і
основні невідо і,		ви рані у п.11.10.2			рис. .	,	. Очевидно,	о й у ц о	у випадку одиничні
епюри	инал ни	о	ентів рис. .		,в, ,д,е,ж	алишат с е		ін і систе	а канонічни рівн н
також ро падет с		на дві не алежні підсисте и.


			ис.11.18
Перша підсисте	а,	о істит к невідо		і лише си етричні сили, внаслідок косо си етрі
епюри инал ни	о	ентів вантажно о стану		рис.	. ,в	ати е нул ові віл ні члени
		11X1	12 X2		14 X4	0;
		12 X1	22 X2		24 X4	0;
		14 X1	42 X2		24 X4	0.

ето	и	28
однорідна систе а рівн н ає тривіал ний ро в ок, то то X1 = X2 = X4 = 0.
Отже,	основні кососи етричні невідо і ожна ви начити, ро в авши дру у	підсисте у

рівн н

35 X3	53 X5	3 p
35 X3	55 X5	5 p

рештою

ожна

дійти

висновку,

симетричній

рамі

під

дією

кососиметричного

навантаження симетричні невідомі напевно дорівнюють нулю.

ео

ідно ви начати лише

кососи

етричні основні невідо

і.

ійсні епюри M і N

удут кососи

етрични

и, а епюра Q

си етричною.

11.10.5. Групові невідомі

а адає

о,

о дістати спро

енн

при ро ра унку си

етрично

конструкці

ожна тоді,

коли

при си

етричній основній систе

і основні невідо

і ро діл ют с

на си

етричні і кососи

етричні,

то то

такі,

привод т

до

си етрични

кососи етрични

епюр

инал ни

ентів

одинични

стана .

попередні

приклада

це виконувалос

авд ки відкиданню

айви

ей

на осі си

етрі

ра

и,

овило прикладанн

невідо

на осі си

етрі .

о при по удові

си етрично

основно

систе

и відкидают с

айві

і,

о не ро ташовані на осі си

етрі ,

одиничні епюри

инал ни

ентів

ожут

ути неси етрични и.

е виключає одержанн

спро ен

ро ра унку. Однак, оскіл ки основні невідо

і є сила и, вони

ожут

ути ро кладені на

си етричні і кососи

етричні складові,

кі становити ут

сукупності невідо

дій і на ивают с

груповими невідомими. Покаже

о це на прикладі.

л не

о ра

у під дією навантаженн

а ал но о ви л ду рис. .

,а).

тупін

статично

неви начуваності n=3k

3 2

2 =

. Основна систе

а,

одержана

ра унок відкиданн

чотир о

опорни

ей,

о ражена на рис. .

, .

Основні невідо

і,

вл ют

со ою реакці

відкинути

опор,

по начи

X1 , X 2 , X3 , X 4 .

и етрично ро ташовані сили

X1 і

X3 , а також

X 2

і X 4

не дорівнюют

одна одній і то

у не

ожут

вважатис

си

етрични

и а о кососи

етрични

и. Беручи до ува и,

о невідо

і,

к і

уд -

кі інші силові ді

ожут

ути ро кладені на си

етричні і кососи етричні складові,

іни

основні невідо

і X1

і X 3

дво

а інши

и сила

и X1

i X3, пов

ани

попередні и сила

и спів-

відношенн

;

ето и							29
причо	у сили X1 прикладе	о си	етрично, а сили X3		кососи		етрично рис. . ,в . Анало ічно
а іни	о дві інші сили X2	і X4 . По начи		о
		X 2	X 2 X 4	;	X 4	X 2	X 4	.
		X 2	2	;	X 4		2	.
			2				2

	ис.11.19
или X2 прикладе о си етрично, а сили X4		кососи етрично	рис.	.	,в . рештою на
основну систе	у ді ти ут сила P, ке є навантаженн	а ал но о ви л ду, си			етричні невідо і
сили X1 i X2,	а також кососи етричні невідо і сили X3 i X4. ожна		ци	нови невідо и сил
фактично становит рупу сил.

ето и

исте а канонічни рівн н оже ути аписана фор ал но

11 X1	12 X 2	13 X 3	14 X 4	1p
21 X1	22 X 2	23 X 3	24 X 4	2 p
31 X1	32 X 2	33 X 3	34 X 4	3 p
41 X1	42 X 2	43 X 3	44 X 4	4 p

0 ;

0 .

цій систе

і основни и невідо и и є

рупові невідо і.

Відповідни

уде також фі ичний

іст рівн н .

априклад, перше рівн нн

свідчит

про те,

лиженн

кінців A i B основно

систе и від всі

дій повинне дорівнювати нулю.

ру е рівн нн

асвідчує дорівнюванн нулю

су арно о вертикал но о пере і енн кінців A i B основно систе

и то

о.

Епюри

инал ни

ентів

від

кожно о

основно о

невідо

о о

від

овнішн о о

навантаженн

по удовано на рис. .

–ж.

к видно, епюри

инал ни

ентів

1 i

2 ,

у овлені дією си етрични

невідо

и , є си

етрични

и, епюри

4 ,

по удовані від ді

кососи етрични

невідо

и ,

кососи

етрични и, а вантажна епюра Mp

епюрою

а ал но о

ви л ду, оскіл ки вона є ре ул тато

ді навантаженн

а ал но о ви л ду.

рештою,

уло вже пока ано,

ви ідна систе

а чотир о

канонічни

рівн н ро падет с

на

дві не алежні підсисте и. Перша підсисте

істит

к невідо

і лише си

етричні сили

11 X1	12 X 2	1p
21 X1	22 X 2	2 p
а дру а лише кососи етричні сили
33 X 3	34 X 4	3 p
43 X 3	44 X 4	4 p

Підсисте и ро в уют с не алежно одна від одно .

ійсні епюри ожут ути по удовані а

спосо о накладанн

1X1

2 X 2

3 X3

4 X 4

M p ;

Q1X1 Q2 X 2 Q3 X3 Q4 X 4 Qp ;

3 X3

4 X 4

N p .

N1X1 N2 X 2

ето

ійсні епюри,

кі є ре ул тато

накладанн

си

етрични

і кососи

етрични

рафіків, удут

епюра

а ал но о ви л ду.

ауважи о,

а нео

ідності виконанн ро ра унку си

етрично

ра и на дію навантаженн

а ал но о ви л ду

ручно ро класти це навантаженн на си

етричну і кососи етричну складові.

ц о

у випадку виконуют с

два окре

і ро ра унки ра

и на дію си

етрично о та на дію

кососи

етрично о навантажен . Остаточні епюри

усил

від ви ідно о навантаженн

а ал но о

ви л ду одержуют с

су

відповідни

епюр,

по удовани

від

йо о

си

етрични і

кососи

етрични

складови

;

11.11. озрахунок статично невизначуваних ферм

о ра унок статично неви начувани

фер

етодо

сил ає де кі осо ливості, кі пов

ані

осо ливост

н о структури, навантаженн

і напружено-дефор

овано о стану

див. лаву ).

ак, ступін

статично неви начуваності фер

ожна о числювати к

а фор улою

11.1 , так і а

іншою фор

улою, при наченою лише дл

фер

n=C+C п

(11.19)

де C кіл кіст

стержнів фер и, C п

кіл кіст

опорни

стержнів,

кіл кіст

ву лів фер

и.

л фер и,

о ражена на рис. . ,а,

2 12

2 .

к о ж скористатис фор улою 11.1 , то ожна аписати

n 3k 3 12 34 2.

ето и

ис.11.20

ає о

той

са

ий

ре ул тат,

але

він

до утий

де

о складніши

ро ра унка

и,

у овлюєт с нео

ідністю о численн

кіл кості прости

шарнірів.

Відкиданн

айви

ей

під

час

при наченн

основно

систе

дійснюєт с

а о

ро рі анн

стержнів фер и, а о відкиданн

опорни

стержнів.

першо

у випадку до

ісц

ро рі у прикладают с

по довжні сили,

величина

ки

невідо а, у дру о

невідо

реакцій

відкинути

опорно

ей рис. . ,

. Проте в усі

випадка

основна систе а повинна

ути

ео етрично не

інюваною.

ци

причин с е

а, о

о ражена на рис. .

,в, не

оже

ути

о рана дл

ро ра унку, оскіл ки

иттєво

інюваною

ву ол D прикріплюєт с

до фер и

дво а стержн

и CD i DE, кі ро ташовані в довж одніє

пр

о .

исте

а канонічни

рівн н

ає вичайний ви л д і дл

фер

и,

о ро

л даєт с ,

оже

ути

аписана в такий спосі

11 X1	12 X 2	1p
21 X 2	22 X 2	2 p

ето

л о численн

коефіцієнтів систе

и рівн н

нео

ідно утворити допо

іжні і вантажний стан

(рис. .

, ,д,е . Оскіл ки в стержн

фер

и виникают лише по довжні сили, фор

ула ора

на увати

е тако о ви л ду:

Ni N j l ;

N pl .

(11.24)

EA0 k 1

i ,

j , N p

ци

фор

ула

по довжні

усилл

в стержн

основно

систе

и відповідно від

ді одинични

невідо

и Xi

= 1, Xj =

і від

овнішн о о навантаженн , EA0

довіл на константа,

ку доціл но покладати такою,

о дорівнює жорсткості на по довжні дефор

аці

ко ос

стержн

фер и, l’

ведені довжини стержнів фер

и,

кі о числюют с

а фор улою

EA0

lk ,

(11.25)

де lk, EAk

довжина і

инна жорсткіст

стержн k фер и.

ійсні

усилл

ожут о числюватис

а спосо о

накладанн

2 X 2

n X n

N p .

(11.26)

N1 X1

11.12. Приклад розрахунку статично невизначуваної ферми

Виконає о ро ра унок статично неви начувано фер и, представлено на рис. . ,а.

ис. .

тержні фер и ают такі жорсткості нижній по с і підвіска– EA;

вер ній по с і стійки 2EA;

ро коси 1,5EA.

ето и

11.12.1. тупінь статичної невизначуваності

тупін статично неви начуваності о числює о а фор улою 11.19):

2 12

Оскіл ки кіл кіст

опорни

ей дорівнює

іні

ал но

ожливій кіл кості,

очевидно,

айви

ожна вважати один

і стержнів решітки.

11.12.2. Вибір основної системи

Основну систе у утвори о шл

ро рі у

ори онтал но о стержн підвіски

рис.

. ,

е ко впевнитис , о перетворена в такий спосі

фер а утворена спосо о

діад і,

отже,

ео етрично не

інюваною.

а основне невідо

е X1

ерет с

усилл , ке ді в

ори онтал но

стержні підвіски.

11.12.3. опоміжний стан основної системи

Ви наченн

опорни

реакцій рис. .

,а

ис. .

ето и

M B	0	VA 12 1 2 1 2 0	VA	0;
M A	0	VB 12 1 2 1 2 0	VB	0;
Fx	0	H A 1 1 0	H A	0.
ри оно	етричні функці кутів на илу стержнів ви начи			о по ео етричній с е і фер и

	sin				l2	7				4				0,8000; cos						l1	2					4		0,6000.
					l1 7															l1 7
								32			42													32		42
								32			42													32		42
	sin			l7		11				2				0,5547; cos						l6	7					3		0,8320.
				l6 11															l6 11
								32			22													32			22
								32			22													32			22
Внутрішні зусилля
а підставі о нак нул ови										стержнів до оди						о висновку,						о стержен					-	є нул ови
															N3	8	0.
Виконавши ро рі						-	ро		л дає о рівнова у ліво половини фер																а	рис.		. , .
						Fy				0				N2 8sin			0						N2	8		0;
						M7				0			N2 3 4 1 2 0										N2 3				0,5;
						M 2				0				N7 8 4 1 6 0									N7 8				1,5.
о л дає		о рівнова у ву лів.
Ву ол	рис.		.			,в
					Fx		0				N2	3		N2 1		N2	8cos					0				N2 1		0,5;
					Fy		0				N2			7 N2		8sin		0								N2	7	0.
Ву ол	рис.		.			,
	Fx	0					N11 6cos							N11 12		0		N11						1			1,202;
																					6
																					6	0,8320
																						0,8320
	Fy	0				N11		7		N11			6sin		0			N11			7			N11 6 0,5547					0,667.
Ву ол	рис.		.			,д
	Fx		0				N6			7	N6 11cos					0	N6 7						N6 110,8320						1,000;
	Fy		0				N6 1				N6 11sin				0		N6 1						N6 110,667					0,667.

ето

Ву ол

рис. .

,е

7sin

N1 6

N1 7

N1 6

0,833;

0,8000

N1 2

N1 7cos

N1 2

N1 7 0,6000

0,5.

е ул тати ро ра унку

усилл

допо

іжно о стану

,ж.

N1 ) наведено на рис. .

11.12.4.

озрахунок основної системи у вантажному стані

ис. .

Визначення опорних реакцій

M B	VA 12 60 9 60 3 0	VA	60	;
M A	VB 12 60 9 60 3 0	VB	60	;
Fx	H A 0.

Внутрішні зусилля

Шіст стержнів основно систе и є авідо о нул ови и

ето	и							37
		N11 12	N7 11	N6 11	N9 12	N10 12	N3	8 0.
л ви наченн		усил	в інши	стержн	скористає	ос	етода	и наскрі ни перері ів та
вирі анн	ву лів.
Перері	I-I рис.	. , .

8sin

N2 8

M 7

N2 3 4 60 3 0

N2 3

;

M 2

N7 8 4 60 4 0

N7 8

Ву ол

рис. .

,в

N2 1

N2 3

8cos

N2 1

;

N2 8sin

N2 7

Ву ол

рис. .

N6 11cos 0

N6 7

N6 1

N6 11sin

N6 1

Ву ол

рис. .

,д

N1 7sin

N1 6

N1 7

N1 6

;

0,8000

N1 2

N1 7cos

N1 2

N1 7 0,6000

наслідок си

етрі

усилл

дл

право половини основно

систе и є д еркал ни

від итт

усил ліво половини.

истема канонічних рівнянь методу сил

наслідок то о,

адана фер

а один

ра

статично

неви начувана,

систе а

канонічни

рівн н

етоду сил складаєт с

одно о рівн нн

11 X1

ке виражає рівніст

нулю в ає

но о на лиженн точок прикладенн основни

невідо

и .

бчислення коефіцієнтів системи канонічних рівнянь

Практичний ро ра унок ра и складаєт с однотипни о числен дл всі стержнів фер и, то у ро ра унок ручно виконувати в та личній фор і див.та л. . ).

ето		и																										38
Перший стовпец				істит		перелік всі							стержнів фер					и.			товпці				і	– довжини стержнів і
жорсткості – ви начают с					по с е і фер и.									ут		вважає о,						о EA0				EA.	ведені довжини
стержнів, о числені				а фор улою			11.25 ,						аписано в стовпец .
усилл в допо іжно у і вантажно												у стана		анесено відповідно в стовпці													і .
оефіцієнти систе и рівн н								ви начают с						а			фор	ула			и 11.24).					О численн		аписані в
стопці	і .	у и чисел в ци				стовпц						дорівнюют				відповідно коефіцієнта 11 та 1P . Отже
										45,602 ,						1116,580 .
					11						EA0			1P						EA0
											EA0									EA0

			EA	l									NP														N	N
т.	l							N	1						N1N1l					NP N1l			N1 X1						N1l
т.	l		EA0					N	1						N1N1l					NP N1l			N1 X1						N1l
1	2	3		4			5						6			7					8					9	10	11
1-2	3	2		1,5		0,5							-45	0,375					-33,750					12,243			-32,757	-24,568
2-3	3	2		1,5		0,5							-45	0,375					-33,750					12,243			-32,757	-24,568
3-4	3	2		1,5		0,5							-45	0,375					-33,750					12,243			-32,757	-24,568
4-5	3	2		1,5		0,5							-45	0,375					-33,750					12,243			-32,757	-24,568
6-7	3	1		3			-1						0	3,000							0			-24,485			-24,485	73,456
7-8	3	1		3		-1,5							45	6,750					-202,500					-36,728			8,272	-37,224
8-9	3	1		3		-1,5							45	6,750					-202,500					-36,728			8,272	-37,224
9-10	3	1		3			-1						0	3,000							0			-24,485			-24,485	73,456
1-6	4	2		2		0,667							-60	0,890					-80,040					16,332			-43,668	-58,254
2-7	4	2		2			0						-60			0					0					0	-60	0
3-8	4	2		2			0						0			0					0					0	0	0
4-9	4	2		2			0						-60			0					0					0	-60	0
5-10	4	2		2		0,667							-60	0,890					-80,040					16,332			-43,668	-58,254
1-7	5	1,5		3,333		-0,833							75	2,313					-208,250					-20,396			54,604	-151,616
2-8	5	1,5		3,333			0						0			0					0					0	0	0
4-8	5	1,5		3,333			0						0			0					0					0	0	0
5-9	5	1,5		3,333		-0,833							75	2,313					-208,250					-20,396			54,604	-151,616
7-11	2	1		2		-0,667							0	0,890							0			-16,332			-16,332	21,786
9-12	2	1		2		-0,667							0	0,890							0			-16,332			-16,332	21,786
6-11	3,605	1		3,605		1,202							0	5,209							0			29,431			29,431	127,532
10-12	3,605	1		3,605		1,202							0	5,209							0			29,431			29,431	127,532
11-12	6	1		6			1						0	6,000							0			24,485			24,485	146,912
														45,602						-1116,580								0,000

ето и

озв’язання канонічних рівнянь

Підставл є о коефіцієнти до канонічно о рівн нн

45,602	X1	1116,580		0.
EA0			EA0

відси

X1 24,485.

бчислення дійсних зусиль в стержнях ферми

ійсні усилл	в стержн	статично неви начувано			фер	и о числи о, а уючис на принципі
не алежності дій	сил, к	су и	усил	в основній	систе	і від основно о невідо о о і від
овнішн о о навантаженн , то то			а фор	улою

N1X1 NP .

о утки

підра овуют с в стовпці

, а дійсні

усилл – в стовпці .

N1X1

Кінематична перевірка результатів розрахунку

е ул тати ро ра унку перевір ют с пере ноженн

дійсни усил в стержн фер и N

на одиничні усилл

1, то то

N1N l .

EA0

Пере ноженн дл кожно о стержн аписуют с в стовпці . у а чисел стовпц дорівнює нулю, то то

1 EA0 N1N l 0.

Отже, ро ра унок виконано правил но.

11.13. озрахунок нерозрізних балок

уціл ну статично неви начувану	алку,	ка	не	перериваєт с		шарніра и, на ивают
.
по л ду кіне атично о аналі у всі опорні в		і,	а вин тко		тр о , є	айви и . Отже ступін
статично неви начуваності алки оже	ути о числений			а фор	улою

n = C 3,

(11.27)

ето

де

кіл кіст

опорни

ей дл

шарнірно-ру о о

опори

1, дл

шарнірно-неру о о

дл

атисненн

3 .

ак,

дл

алки,

пока ана

на

рис.

,а,

ступін

статично

неви начуваності n=7

3 = 4.

тупін

статично

неви начуваності

алки

оже

ути

також

о числений

а фор улою

n=3k .

11.13.1. Рівняння трьох моментів

Основна

систе

а дл

ро ра унку неро рі но

алки

етодо

сил

оже

ути

утворена

відкиданн

уд -

ки

ей,

ожут

ро л датис

айві .

ак,

ожна відкинути всі

про іжні шарнірно-ру о і

опори.

оді

основна

систе а становити е статично ви начувану і

ео

етрично не

інювану

алку на дво

опора ,

до

ко

ра о

і овнішні

и навантаженн

прикладені реакці

відкинути

опор X1,

X2, X3

к сили невідо

величини.

оч така

основна систе а фор ал но і є правил ною, ра о

і ти

вона вкрай нераціонал на.

ис.11.24

ето

ро ра унку

неро рі ни

алок слід

використовувати

апропоновану Б.П. лапейроно

стандартну основну систе

у,

о утворюєт с

постановкою шарнірів над опора и

рис.

. 4, .

исте

вл є со ою сукупніст

окре и

однопро онови алок,

кі дефор

уют с

не алежно

одна від одно .

у ді

овнішн о о навантаженн

одніє

однопро оново

алки на іншу не

передаєт с . Основни и невідо

и в дано

у випадку є

инаючі

о енти, о виникают

у пере-

рі а

алки над

опора и, так вані опорні моменти.

неро рі но

алки,

о ро

л даєт с , систе а канонічни

рівн н ати

е такий ви л д

11X1	12 X2	13 X3	14 X4	1p
21X1	22 X2	23 X3	24 X4	2 p
31X1	32 X2	33 X3	34 X4	3 p
41X1	42 X2	43 X3	44 X4	4 p

Одиничні і вантажна епюри

инал ни

ентів по удовані на рис. .

,в, ,д,е,є.

а підставі то о, о де кі епюри не

ают

спіл ни

діл нок,

ожна аписати

41 42 0.

исте

а канонічни рівн н

ура уванн

ц о о

ати

е такий ви л д

11X1

12 X2

21X1

22 X2

23 X3

2 p

32 X2

33 X3

34 X4

3 p

43 X3

44 X4

4 p

ачи о,

в кожно у рівн нні,

крі

першо о та останн о о, тіл ки три коефіцієнти при

невідо

від

інні від нул

оловний і два сусідні

ни .

о у довіл не рівн нн

ати

ви л д

i,i 1 X i

i,i X i

i,i 1 X i 1

0 .

л не о

епюри, нео

ідні

дл

о численн

коефіцієнтів ц о о

рівн нн .

рис. .

о ражено фра

ент неро рі но

алки та епюри

инал ни

ентів від одинични

невідо и

та

від овнішн о о навантаженн .

О числи о коефіцієнти рівн нн

а фор

улою

ора

ето и

i,i 1

i,i

i,i 1

1 1

Mi 1

EIi

i 3

6EIi

1 1

li 1

MiMi

1 l

EIi 2

EIi 1 2

i 1 3 3EIi

3EIi 1

1 1

li 1

MiMi 1

EIi 1 2

i 1 3

6EIi 1

		iM p		1		1
	M	iM p	dx	1	y	1	y	.
			dx		y		y	.
	EI			EIi	p,i i	EIi 1	p,i 1 i 1
l	EI			EIi		EIi 1
l

ис.11.25

Післ підстановки пере і ен до рівн нн та де ки перетворен одержи о остаточно

i 1

2( l

i 1

B .

li 1

A . .

(11.28)

li 1

i 1

ето

ут по начено

li ,li

ведені довжини про онів,

кі о числюют с

а фор

ула и

li ,

EIi

li 1

1 , де EI

жорсткіст

на

ин одно о

про онів

алки,

ка о ираєт с

а основну

EIi

. ,Ai 1.

фіктивні опорні реакці

на опорі

в про она

li і li+1

відповідно.

л ви наченн

фіктивни

опорни

реакцій нео

ідно по удувати епюри Mp від

овнішн о о

навантаженн

в ци

про она ,

к в окре

однопро онови алка .

і епюри слід ро

л дати

де ке фіктивне навантаженн ,

овлює по ву о начени

фіктивни реакцій.

а рис. .

пока ано дві с е и фіктивно о навантаженн

і фіктивни опорни

реакцій ро

л нуто

алки.

ис.11.26

наченн фіктивни

реакцій опор дл

де ки

про онови

навантажен

наведено в одатку .

аписане рівн нн

слушне лише в то у випадку,

о основна систе

а одержана постановкою

шарнірів над опора и і основні невідо і

вл ют

со ою опорні

енти, то то Xi-1

Mi-1,

Xi Mi, Xi+1 Mi+1.

о у це рівн нн

часто

аписуют так

2( l

B .

A .

(11.29)

i 1

і на ивают	. и	рівн нн	ожна скористатис	дл	фор ал но о
складанн систе и канонічни рівн н	етоду	сил, к	о неро рі на алка	ає	стандартний
ви л д, то то ає на кінц шарнірні опори.

ето

перейти до стандартно с е

и потрі но

відкинути консолі,

к о

вони

є, а атисненн а

інити

на

фіктивні

про они нул ово

довжини

прону

ерувати опори ліва направо

прону

ерувати про они в такий спосі ,

ні но

ери відповідали но

ера прави

опор

про онів.

ак, ро ра ункова

с е а

неро рі но

алки

рис.

. ,а

інена стандартною

с е ою

рис. .

, .

ис.11.27

викладено о

випливає,

дл

складанн

систе и

канонічни

рівн н

етоду сил дл

неро рі но

алки не о ов'

ково

удувати одиничні епюри в основній систе

і і о числювати

пере і

енн

а фор

улою

ора.

ілко

достатн о аписати рівн нн

тр о

ентів 11.28 а о

(11.29 дл

кожно

про іжно

опори стандартно с е

алки, надаючи індексу i почер ово о

наченн ,

то

о.

л не

о о численн

дійсни

усил

у довіл но

у про оні неро рі но

алки li. користа-

є ос спосо о

накладанн

i Xi

M p .

i 1

Оскіл ки в довіл но у про оні li лише дві одиничні епюри,

о від

інні від нул , апише о

i 1Xi 1

i Xi

M p .

уд - ко о перері у

координатою z рис. .

ожна

аписати, о

M z

( l

z )

M z .

(11.30)

ето и

				ис.11.28
Продиференціювавши цей вира , дістане					о фор улу			дл о численн поперечни	сил	у
довіл но у перері і	уд - ко о про ону неро рі но						алки
			z dM z			Mi	Mi 1	z
		Q						Qp .	(11.31)
		Q		dz			li	Qp .	(11.31)
				dz			li
Опорні реакці	ожут	ути о числені			ви од чи			рівн н рівнова и опорни	в	ей
рис.11.29):

ис. .

Fy 0 Ri Qi 1 Qi ,

(11.32)

де Qi+1 i Qi поперечні сили відповідно праворуч і ліворуч опори.

ето и

11.13.2. Метод моментних фокусів

етод	о ентни	фокусів	е посередн о випливає ро ра унку а допо	о ою рівн н	тр о
о ентів	неро рі ни	алок,	у ки навантажено лише один про ін. о	л не о таку	алку
рис. .	,а .

ис.11.30

Епюра

инал ни

о ентів,

одержана

авд ки ро ра унку,

по удована на рис. .

, .

аналі у ціє епюри

ожна дійти таки

висновків

у іру віддаленн від

авантажено о про ону опорні

о енти

еншуют с

наченн

на кожно у ненавантажено

у про оні епюра M пр

олінійна і перетинає віс

алки,

то то

ає нул ову точку.

ю точку на ивают

моментним фокусом ц о о про ону.

алежно

від

ро ташуванн

навантаженн

одо дано о про ону

ро рі н ют ліві

праві

ентні фокуси. Лівим фокусом на ивают

нул ову точку епюри M у ненавантажено

у про оні,

о він ро ташований ліворуч від навантажено о про ону точки F1, F2,

на рис.

. , .

Анало ічно ви начают с

праві фокуси

точки F5 ,F6 ).

ожно у

фокусу

відповідає

де ке

додатне

число,

ке

на иваєт с

фокусним

співвідношенням.

Воно

арактери ує

співвідношенн

опорни

ентів

на

кінц

дано о

ненавантажено о

про ону.

ак,

дл

фокуса

рис. .

фокусне

співвідношенн

k1=

M1/M0 =

дл

фокусів F2

і F3

фокусне співвідношенн k2 =

M2/M1 i

k3=

M3/M2.

в а алі дл

довіл но о про ону li

рис.

,а

ліве фокусне співвідношенн

(11.33)

ето	и	47
Величина	фокусно о співвідношенн ви начає ро ташуванн фокуса в про оні	алки
рис. . .

ис.11.31

ео етрични іркуван

li ai

M i

відки відстан

ai виражаєт с

чере

фокусне співвідношенн

алежністю

(11.34

Анало ічні

алежності

ожна

аписати дл прави

фокусів.

ак, дл

фокусів

F5, F6

фокусні

співвідношенн

ают

ви л д

M 4

M 5 ,

M 6 .

право

у фокусі Fi

довіл но о про ону li

рис.

відповідне фокусне співвідношенн виражаєт с

фор

улою

M i 1

(11.35)

M i

а відстан право о фокуса до право опори про ону фор улою

(11.36)

л ви наченн величин фокусни співвідношен ро л не о ку-не уд неро рі ну алку рис. . .

ето и

ис.11.32

апише о рівн нн тр о о ентів 11.29 почер ово дл кожно про іжно опори. л опори

1 ( 1)

l M

2( l l

A ).

Оскіл ки

про она

i l2 відсутнє

овнішнє

навантаженн ,

то фіктивні опорні

реакці

0 .

акож дорівнює нулю опорний

ент на крайній опорі Mo =0.

рештою

ає о

2( l1

l2 )M1

l2 M 2

відки

оже

аписати

M 2

2( l1

)

k2 const .

опори

=2)

l2 M1 2( l2 l3 )M 2 l3 M 3

ут вра овано, о

овнішнє навантаженн

в про она

i l3

відсутнє.

Післ нескладни

перетворен

ає о

M 3

const .

M 2

Продовжуючи такі са і аписи дл наступни опор, оже о рештою аписати ліве фокусне співвідношенн дл довіл но о про ону i у ви л ді

ki	2	li 1	2	1		.	(11.37)
				ki
		li			1

Анало ічну фор улу ожна одержати і дл прави фокусни співвідношен

ето

li 1

(11.38)

ео

ідно

вернути ува у на те, о фокусні співвідношенн

алежат

тіл ки від фі ико-

ео

етрични

арактеристик

алки

не

алежат

від

ро ташуванн , арактеру

величини

навантаженн .

відси

випливає,

точки

о ентни

фокусів

також

не

алежат

від на-

вантаженн

вл ют со ою де кі константи неро рі но

алки.

ор

ула

11.37 дає

о у о числити

фокусне

співвідношенн

в про оні li,

відо

фокусне

співвідношенн

попередн о

про оні

li-1,

а дл о численн

право о

фокусно о

співвідношенн

а фор

улою

11.38

потрі но

ати співвідношенн

у про оні li+1.

аки

чино

о численн

ліви

фокусни

співвідношен

нео

ідно ро починати

ліво о, а прави

право о

кінц

алки.

рі

то о,

нео

ідно

нати ліве фокусне співвідношенн

у крайн о

у ліво у і праве

фокусне співвідношенн

у крайн о

у право у про оні, кі алежат

від виду крайн о

опори.

величини о ражені на рис. . .

				ис.11.33
л	ро ра унку неро рі но		алки	а етодо	о ентни	фокусів нео	ідно також ви начити
опорні	о енти по кінц	навантажено о про ону.			цією етою ро л не		о фра ент алки, кий
істит	цей про ін рис.	. ,	ра о і	очікуваною епюрою		инал ни о	ентів.

ис.11.34

ето

апише о рівн нн

тр о

ентів дл

опор по кінц

навантажено о про ону.

Опора i-1:

i 2

2( l

l )M

i 1

l M

i 1

ут вра овано,

о внаслідок відсутності навантаженн

у про оні li-1 фіктивна реакці

Опора :

i 1

2( l

li 1

B .

li 1

е два рівн нн

дістане о, ви од чи

фокусни

співвідношен

у ненавантажени

про она

ki 1;

1 .

о в

авши чотири рівн нн

відносно опорни

ентів на кінц

навантажено о про ону

ає о, рештою

ає

;

(11.39)

kiki

(11.40)

kiki

Отже,

оже

ути

апропонована така процедура ро ра унку неро рі но

алки

о числити фокусні співвідношенн

а фор ула

11.37 і 11.38);

ви начити опорні

о енти на ліво у і право

у кінц

навантажено о про ону а фор

ула

(11.39) – (11.40);

пере і

уючис

вліво

відносно

навантажено о

про ону, о числити опорні

енти

на

наступни опора

чере

ліві фокусні співвідношенн

( M j

M j 1 / k j

1 );

пере і

уючис відносно

авантажено о про ону в правий

ік, о числити опорні

енти на

наступни опора

чере

праві фокусні співвідношенн

( M j

M j 1 / kj ).

а фор

ула и

11.30)

(11.32

ви начити внутрішні

усилл

в про она

алки і опорні реакці .

11.13.3. Побудова огина чих еп р

авантаженн ,	о діют на удівел ну конструкцію,	ожут	ути постійни и а о
ти часови и. к	постійне навантаженн ро л даєт с власна ва а		алки. Ва а о ладнанн і

ето

вантажів,

кі ро ташовуют с

на

алці і в процесі експлуатаці споруди

ожут

інювати сво

величини

та

положенн ,

ро

л дают с

ти

часові навантаженн .

аки

чино

внутрішні

усилл

це су

усил

від ді постійно о і ти

часови

навантажен . Проте оскіл ки величини і

ро ташуванн

ти

часови

навантажен

ожут

інюватис ,

інювати

ут с

і су арні наченн

усил . Під час проектуванн

важливо

нати екстре

ал ні величини

усил ,

кі ожут

виникнути

в систе і

уд -

ки ожливи

ін ти часово о навантаженн .

і ро ра унки дл

уд -

ко о

перері у

алки k

ожут

ути виконані

а допо о ою фор ул

Smaxk

Sпk

(

S k

);

(11.41)

Smink

Sпk

(

S k

ци

фор

ула

Smaxk

, Smink

акси

ал ні і

іні

ал ні усилл в перері і k від ді

постійно о і

ти часови

навантажен ,

Sпk

усилл

від ді

постійно о навантаженн , (

S k

),(

S k

)

відповідно додатні і від є

ні величини

усил

при перед ачувани ти

часови

навантаженн .

алка

о числюют

акси ал ні і

іні

ал ні

инал ні

о енти і поперечні сили

Mmaxk

Mпk

(

M k

);

Mmink

Mпk

(

M k

);

(

);

max

( Qk

min

Епюри

M max , M min , Qmax , Qmin ,

арактери уют

акси

ал ні і

іні

ал ні

инал ні

о енти і поперечні сили,

кі

виникают

перері а

алки а уд - ки

перед ачувани

ти часови

навантажен , на ивают о инаючи и о відни и

епюра

и внутрішні

усил .

11.14. собливості розрахунку статично невизначуваних комбінованих систем

іновани

и систе а и на ивают с

такі,

ают у своє

у складі еле

енти, кі піддані

ину

алки, ра

и, арки , так і еле енти,

кі

ают

лише по довжні дефор аці

фер

и, стержні і

шарнірни

приєднанн

о о кінців .

тупін

статично

неви начуваності ко

іновани

систе кра

е о числювати

а фор

улою

(11.1 , перера овуючи складні шарніри у прості.

Основна систе

о ираєт с

а а ал ни и

правила и, систе а канонічни

рівн н

дл

ви наченн

основни

невідо и

ає стандартний ви л д.

ето	и						52
ак, дл	алки,	ка підсилена фер	ою	рис. . 5,а , ступін статично неви начуваності
		n	3	3	4	11	1.
Основна систе		а, о одержана шл		о ро рі у стержн			фер и, о ражена на рис. . 5, .

			ис.11.35
исте а ро в	увал ни рівн н	істит	лише одне рівн нн
		11X1		1P	0.
тержнева систе а на рис. . 5,в є ко			інацією дво			консол ни алок фер		ою.	тупін
статично неви начуваності
	n	3k		3 9	24		3.
Основну систе	у, ка одержана відкиданн			опорни		в	ей, наведено на рис.	. 5, .	исте а
ро в увал ни рівн н ає ви л д

11X1	12 X2	13 X3	1P
21X1	22 X2	23 X3	2P
31X1	32 X2	33 X3	3P

Основна від інніст	ро ра унку ко іновани систе пол ає в	о численні коефіцієнтів і
віл ни членів систе и	канонічни рівн н , дл чо о використовуєт с	фор ула ора у ви л ді

(11.42)

i M p

i N p

перші доданки	ци фор	ул в од т	инал ні о енти одинични та вантажно о станів
основно систе и, о	виникают	лише в еле	ента алок, ра , арок. В дру и доданка ерут с

11.Метод сил

до уваги поздовжні сили лише в елементах, що зазнають тільки поздовжніх деформацій (ферми,

прямолінійні стержні, приєднані шарнірами на обох кінцях). Впливом на значення коефіцієнта чи вільного члена поздовжніх сил в елементах, що зазнають згину, можна знехтувати. Дійсні зусилля можуть бути обчислені за формулами (11.20).

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>