Добавил:

Punk0tta bettaalpha553@gmail.com Discord @punk0tta#0252 TG punk0tta Inst v_is_vsevolod Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет строительства и архитектуры

Предмет:

Сопротивление материалов

Файл:

BUDMECH.pdf

Скачиваний:

Добавлен:

21.05.2021

Размер:

26.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>

ДО ЗМІСТУ ПІДРУЧНИКА

18. Метод скінченних елементів у задачах динаміки

З м і с т г л а в и

18.1. Скінченно-елементнан модель динамічноїн системи

18.2. Дискретизація розподілених мас у методі скінченних елементів

18.3. Вузловін характеристикин скінченно-елементноїн моделі

18.4. Матриця зосереджених мас

18.5. Рівняннян динамічноїн рівновагин вузлівн скінченно-елементноїн моделі

18.6. Розрахунок на вільні коливання

18.7. Приклад розрахунку на вільні коливання

18.8. Змушені коливання при гармонічному навантаженні

18.9. Приклад розрахунку на змушені коливання

Розглянемо застосування методу скінченних елементів у формі методу переміщень, який обговорювався в Гл.6, для розв’язання динамічних задач. Силами опору руху знехтуємо.

18.1. Скінченно-елементнаП модельП динамічноїП системиП

Для застосування методу скінченних елементів розрахункова схема стержневої системи має бути замінена її дискретною моделлю, що складається з прямолінійних стержнів постійної жорст-

кості і окремих точок − вузлів. У задачах статики за вузли приймалися точки поєднання двох або кількох стержнів, точки прикладання зовнішніх зосереджених мас, сил і моментів, місця ступінчатої зміни жорсткості та опорні вузли. В задачах динаміки до вузлів також додаються точки, н в н якихн н розташованон н зосередженін н масин. н Стержнін, н які н поєднуютьн н вузлин н скінченно-елементноїн моделі, н розглядаютьсян н як н стержневін н скінченнін н елементин. н Координатин н вузлівн н скінченно-елементноїн моделі визначаються в глобальній системі координат. Розподілена маса стержнів замінюється точковими н масамин, н прикладенимин н до н вузлівн. н Отже, н скінченно-елементнан н модельн н складаєтьсян н з

невагомих стержнів постійної жорсткості.

m1, m2 , m3 .

~ ~ ~

m1, m2 , m3

18.Метод скінчених елементів в задачах динаміки

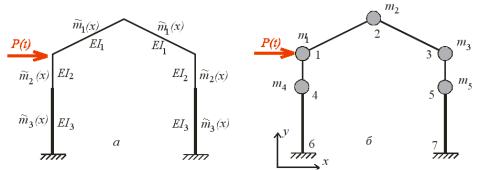
Приклад н переходу н від н розрахункової н схеми н до н скінченно-елементної н моделі н зображено н а рис.18.1.

Рис.18.1

Розрахункова схема рами (рис.18.1,а) складається зі стержнів з рівномірно розподіленими масами. Рівномірно розподілена маса і жорсткість на згин елементів ригеля становлять відповідно

~	(x) і	EI1 .	Стояки мають ступінчастий характер: розподілена маса і жорсткість верхньої
m1
частини –		%	( x)	і EI	~	(x) та	EI 3 . На раму діє узагальнена динамічна сила P(t).
		m2			2 , нижньої – m3

Скінченно-елементна н модель н заданої н розрахункової н схеми н зображена н а н рис.18.1,б. н Вона складається з невагомих стержнів постійної жорсткості EI1 , EI 2 , EI 3 , які з’єднуються між собою у вузлах. Розподілені маси стержнів замінено точковим масами, що прикладені до вузлів.

Для н позначення н геометричних н характеристик н скінченно-елементної н моделі н введено н глобальну систему координат xy. Усі зазначені точки, разом з опорними точками, складають вузли скінченно-елементної моделі, а стержні, які з’єднують вузли, являють собою скінченні елементи.

18.2. Дискретизація розподілених мас у методі скінченних елементів

При виконанні за методом скінченних елементів динамічного розрахунку стержневих систем із розподіленими масами можливі два підходи до дискретизації розподілених мас. Перший підхід базується на тому, що сумарна маса кожного стержня зосереджується на його кінцях, тобто в точках визначення поступальних переміщень.

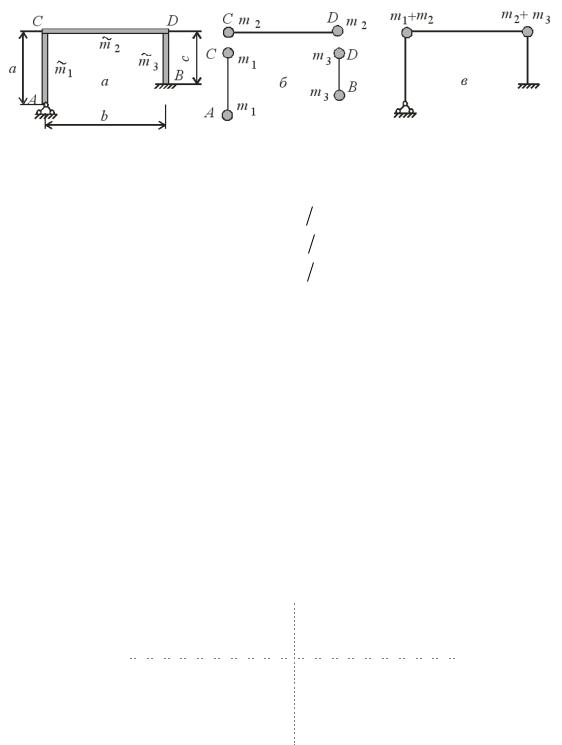
Наприклад, раму (рис.18.2,а) з розподіленими масами на стержнях розіб’ємо на три ділянки, і масу кожної ділянки порівну розподілимо між її кінцями (рис.18.2,б) у вигляді точкових мас

18.Метод скінчених елементів в задачах динаміки

Рис.18.2

Таким чином
m1	~
m1	= m1a 2,
m2	~
m2	= m2b 2,
m3	~
m3	= m3c 2.

В результаті задану схему замінюємо невагомою рамою (рис.18.2,в) з двома точковими масами,

кожна з яких дорівнює сумі точкових мас на стержнях у відповідних вузлах.

При другому підході вважається, що в процесі коливань сили інерції у стержнях розподіляються пропорційно до переміщення їхніх осей залежно від граничних умов, тобто визначаються функціями форми. Ці нерівномірно розподілені сили зумовлюють кінцеві реакції,

які, в свою чергу, залежать від граничних умов стержнів. Інерційні сили характеризують деякі уявні маси, які вважаються розташованими на кінцях стержня і можуть переміщуватися в тому чи в іншому напрямі і утворюють матрицю розподілених мас стержня в локальній (18.1) або глобальній системі координат:

	m′			m′	m′	m′	m′	m′
			11	12	13	14	15	16
			′	′	′	′	′	′
	m21			m22	m23	m24	m25	m26
			′	′	′	′	′	′
′	=	m31		m32	m33	m34	m35	m36
′			′	′	′	′	′	′		(18.1)
me			′	′	′	′	′	′		(18.1)
	m41			m42	m43	m44	m45	m46
			′	′	′	′	′	′
		m51		m52	m53	m54	m55	m56
		m51		m52	m53	m54	m55	m56
			′	′	′	′	′	′
	m61			m62	m63	m64	m65	m66	e
Будь-який елемент m′			матриці розподілених мас m′				характеризує значення сили інерції,
	ij					e

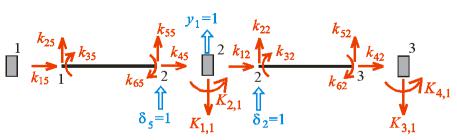
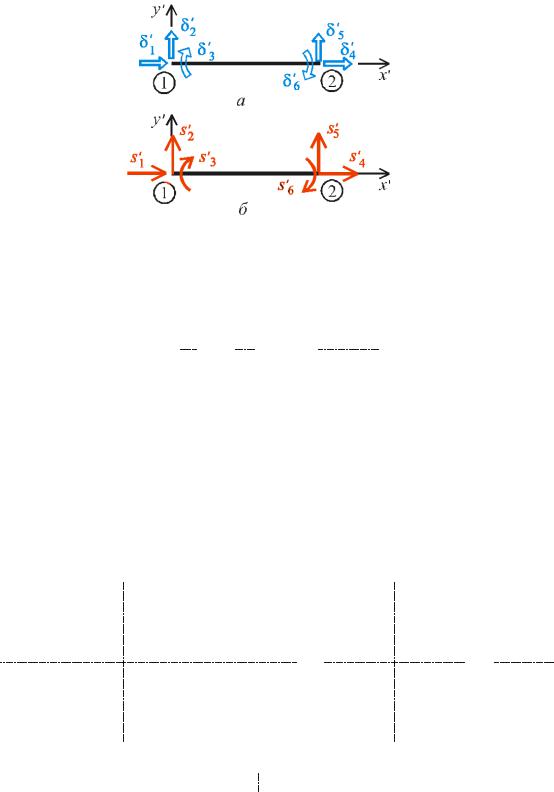
яка спрямована в напрямі і від примусового переміщення δ′j = 1. Так, на рис.18.3 зображено

елементи матриці розподілених мас від примусового переміщення δ′5 = 1 .

18.Метод скінчених елементів в задачах динаміки

Рис.18.3

Значення елементів матриці розподілених мас стержня в локальній системі координат ви-

ражаються через величину рівномірно розподіленої маси і функції форми стержня (див.6.4) за формулою:

		l		(x¢)× F		(x¢)dx .
m¢	= m	∫	F	(x¢)× F	j	(x¢)dx .	(18.2)
ij		∫	i		j
		0

Так, для скінченного елемента першого типу (затиснення на обох кінцях стержня) побудована за допомогою формули (18.2) матриця розподілених мас в локальній системі координат має такий вигляд:

			140		0	0	70	0	0
				0	156	− 22l	63	54	13l
′					− 22l		−14l	−13l
′	=	ml	0		− 22l	4l 2	−14l	−13l	− 3l 2
me				70	0	0	140	0	0	.	(18.3)
me		420								.	(18.3)
		420
				0	54	−13l	0	156	22l
						− 3l 2			4l 2
			0		13l	− 3l 2	0	22l	4l 2	e

Матриця розподілених мас скінченного елемента в глобальній системі координат може бути отримана за допомогою матриці перетворення:

m	e	= TT m¢ T ,	(18.4)
	e	e e e

де матриця перетворення Te визначається співвідношенням (6.8).

Матриця н розподілених н мас н скінченно-елементної н моделі н може н бути н побудована н аналогічно матриці жорсткості за допомогою структурної матриці або шляхом почергового надання одиничних вузлових переміщень з подальшим підсумовуванням відповідних елементів матриць розподілених н мас н скінченних н елементів. н Отже, н матриця н розподілених н мас н скінченно-елементної моделі матиме недіагональні коефіцієнти. Структура її буде аналогічною до структури матриці жорсткості.

18.Метод скінчених елементів в задачах динаміки

18.3. Вузлові характеристики скінченно-елементної моделі

Кожен н вузол н скінченно-елементної н моделі н має н кінематичні н і н силові н характеристики. н Всі н ці

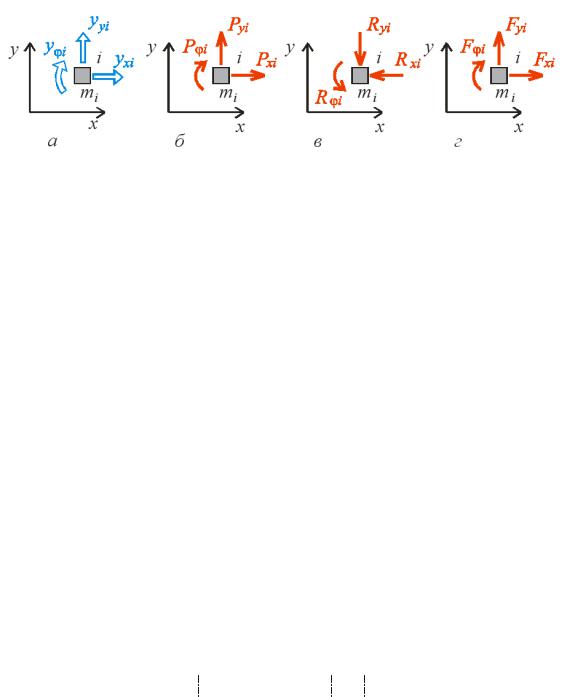
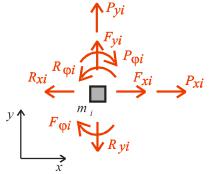
величини є функціями часу. Вважається, що переміщення будь-якого жорсткого вузла i характери-

зується двома поступальними переміщеннями yxi i y yi вздовж осей глобальної системи

координат, а також кутом повороту yϕi (рис.18.4,а). Сукупність цих переміщень становить вектор

r	= { yxi	yyi yϕi } . Отже жорсткий вузол на площині має три ступні
переміщень вузла yTi	= { yxi	yyi yϕi } . Отже жорсткий вузол на площині має три ступні
вільності.

Рис.18.4
На рис.18.4,б зображено зовнішні динамічні навантаження P , P , P		, а на рис.18.4,в −
xi yi	ϕi

вузлові реакції Rxi , Ryi , Rϕi , які передаються на вузол з боку деформованих стержнів. Ці величини утворюють вектори

r			Pϕi } ,
PiT = {Pxi		Pyi
r	= {Rxi		Rϕi } .
RTi		Ryi

На відміну від статики в задачах динаміки на зосереджені маси системи, діють сили інерції

Fxi , Fyi , Fϕi , компоненти яких наведено на рис. 18.4,г. Отже вектор сил інерції у вузлі i матиме

вигляд

rT = { }

Fi Fxi Fyi Fϕi .

На базі наведених векторів можна записати вектори вузлових характеристик скінченно-елементної н моделі. н Так, н якщо н скінченно-елементна н модель н має m н вільних н вузлів, н то вектор вузлових переміщень матиме вигляд

r	r	r		r		} =
yT = {y		y	2	K y	m	} =
	1		2		m
= { yx1 yy1 yϕ1	yx2	yy2		yϕ2 K yxm yym yϕm} .

18.Метод скінчених елементів в задачах динаміки

Кількість компонентів вектора вузлових переміщень y визначає кількість ступнів вільності

скінченно-елементної нмоделі. нПри нрозв’язанні н конкретних нзадач нвсі нможливі нпереміщення нв нмежах всієї н скінченно-елементної н моделі н умеруються н підряд. н Отже, н якщо н скінченно-елементна н модель має n ступнів вільності, то вектор вузлових переміщень матиме вигляд:

r	y			y		} .
yT = { y		2	K		n
1

Аналогічно можуть бути записані вектори вузлових навантажень P , вузлових реакцій R і сил інерції F всієї скінченно-елементної моделі:

r		P	K P		} ;
PT = { P
r	1	2		n			};
		R		R
RT = {R			K
r	1	2			n
		F		F		}.
FT = {F			K
	1	2		n

18.4. Матриця зосереджених мас

Сили інерції, які зумовлюються переміщеннями зосередженої маси, можуть бути виражені через відповідні прискорення. Так, для вузла і можна записати:

Fxi = −mi &y&xi ;
Fyi	= −mi &y&yi ;	(18.5)
Fϕi	= −I zi &y&ϕi ,

або в матричній формі:

				r
		Fi = −miyi			,			(18.6)
де
		m		0		0
m	i	=	0i	m		0		(18.7)
	i			i
			0	0		I
							zi

–н матриця н мас н вузла i н скінченно-елементної н моделі. н Величина I zi − це момент інерції маси mi

відносно н вісі z, н перпендикулярної н до н площини н скінченно-елементної н моделі. н Якщо н зосереджені

маси є точковими, то можна вважати, що моменти інерції I zi = 0. У цьому випадку

		m		0	0
m	i	=	0i	m	0 .	(18.8)
	i			i
			0	0	0

18.Метод скінчених елементів в задачах динаміки

На нбазі нматриць нмас нокремих нвузлів нможна нпобудувати нматрицю нмас нвсієї нскінченно-елементної моделі. Так, якщо скінченно-елементна модель має m вільних вузлів, матриця мас матиме вигляд

m1
	m2
M =	m2	.	(18.9)
M =		.	(18.9)
	K

		mm

Зазначимо, що матриця зосереджених мас завжди має діагональну структуру. Кількість рядків матриці н дорівнює н кількості н ступнів н вільності н скінченно-елементної н моделі. н Елементи, н які відповідають силам інерції, що зумовлюються поворотами точкових мас, дорівнюють нулю.

Таким н чином, н можна н вважати, н що н сили н інерції н всієї н скінченно-елементної н моделі н визначаються матрицею мас:

r	(18.10)
&&
F = −My.

18.5. Рівняння динамічної рівноваги вузлів скінченно-елементної моделі

Прикладемо до будь-якої зосередженої маси mi всі зовнішні сили (рис.18.5).

Рис.18.5

Оскільки до вузла поряд із зовнішніми навантаженнями прикладено сили інерції, то базую-

чись на принципі Даламбера, можна розглядати вузол як такий, що знаходиться у стані динамічної рівноваги. Зрештою маємо:

∑Fx = 0	− Rxi + Pxi + Fxi = 0;
∑Fy = 0 − Ryi		+ Pyi	+ Fyi = 0;
∑M = 0	− Rϕi	+ Pϕi	+ Fϕi = 0.

18.Метод скінчених елементів в задачах динаміки									8
Перепишемо ці рівняння в матричній формі:
−		i +		i +		i =		.
	R		P		F		0		(18.11)

Склавши н аналогічні н рівняння н для н кожного н з m н вільних н вузлів н скінченно-елементної н моделі,

отримаємо загальну систему рівнянь динамічної рівноваги. В матричній формі маємо:

r r r
−R + P + F = 0 .	(18.12)

Враховуючи, що вузлові реакції можна виразити через вузлові переміщення за допомогою матриці жорсткості скінченно-елементної моделі

r	(18.13)
R = K y ,

а сили інерції виражаються через другі похідні від переміщень співвідношеннями (18.10), надамо рівнянню (18.12) остаточного вигляду:

	r
&&	+ Ky = P .	(18.14)
M y	+ Ky = P .	(18.14)

Матричне диференціальне рівняння динамічної рівноваги може бути записане в координатній формі:

&&	+ K y	+ K	y		+ K + K	y		= P ,
m y				2			n
1 1	1,1 1	1,2			1,n			1
&&	+ K2,1 y1	+ K2,2 y2			+ K + K2,n yn = P2 ,
m2 y2
								(18.15)
L L L L L L L L L L L
&&	+ Kn,1 y1	+ Kn,2 y2			+ K + Kn,n yn = Pn .
mn yn
У цих співвідношеннях, як і раніше, через					Ki , j позначено вузлову реакцію Ri , зумовлену
одиничним вузловим переміщенням		y j = 1.

18.6. Розрахунок на вільні коливання

Вільними коливаннями вважаються такі, що відбуваються за відсутністю зовнішніх динамічних навантажень. Диференціальні рівняння динамічної рівноваги в цьому випадку можуть бути одержані із співвідношення (18.14), якщо вважати вектор вузлових навантажень нульовим

P = 0 . Отже, можна записати:

&&	r
	+ Ky = 0 ,	(18.16)
M y

або в координатній формі:

ето

інчени е ементів в а ача инамі и

m1y1

K11, y1

K1,2 y2

K1,n yn

m2 y2

K2,1y1

K2,2 y2

K2,n yn

mn yn

Kn,1y1

Kn,2 y2

Kn,n yn

к і у п.п. . .

уде

о ро шукувати ро в

ок систе и диференціал ни рівн н

ви л ді

ар онічни

функцій

a sin

2sin

;

a sin

2sin

;

a sin

2sin

атричній фор

і ці співвідношенн

ати ут

ви л д

Vsin

2Vsin

де VT

a1 a2 an

вектор а

плітуд ву лови

пере

і ен .

Післ

підстановки ро в

ку .

у рівн нн

18.16

дістане

о ал е ра чне рівн нн

2M V 0.

(18.17)

. у

(18.18)

(18.19)

(18.20)

е співвідношенн			еквівалентне систе і однорідни ал е ра чни					рівн н	відносно а плітуд
ву лови пере	і ен
K11,	m1	2 a1		K1,2a2			K1,nan		0;
K2,1a1				K2,1 m2	2 a2		K2,nan		0;
									(18.21)

Kn,1a1				Kn,2a2		Kn,n	mn	2 an	0.

систе	и рівн н	.	випливає,	о принай ні де кі а плітуди пере			і ен	удут
від інни и від нул		то то	існувати ут	віл ні коливанн	скінченноеле	ентно	оделі ,	к о
дорівнювати	е нулю детер інант, складений і коефіцієнтів				при невідо и	пере і	енн

18.Метод скінчених елементів в задачах динаміки

− m ω2

1,1

1,2

1,n

− m ω2

Det =

= 0 ,

(18.22)

K K

n ,n

− m ω2

або

Det =

K − ω2M

= 0 .

(18.23)

Рівнянню (18.23) може бути надана традиційна форма задачі на власні значення:

A − λE

= 0 ,

(18.24)

де

A = M−1K ,

(18.25)

λ = 1 ω2 .

(18.26)

При н побудові н матриці н жорсткості K н враховувалися н всі н ступні н вільності н скінченно-елементної моделі, в тому числі й кути повороту точкових мас, які насправді дорівнюють нулю, і тому матриця мас має нульові рядки і стовпці. Такі ступні вільності будемо називати фіктивними.

Тому при побудові матриці A необхідно виключити з матриць жорсткості K і матриці мас M

рядки і стовпці, які відповідають фіктивним ступням вільності.

Розв’язок рівняння (18.24) визначає власні числа λ і відповідні цим числам власні вектори V .

Власні числа характеризують частоти вільних коливань:

ω = +

(18.27)

а власні вектори − головні форми коливань.

18.7. Приклад розрахунку на вільні коливання

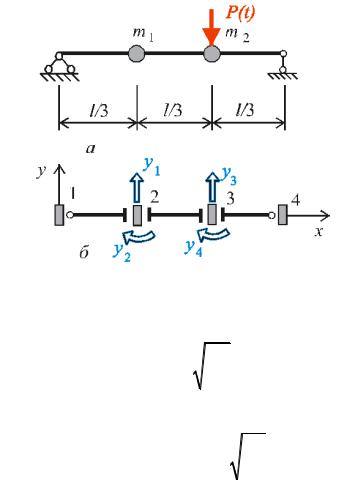
Визначити колові частоти і форми вільних коливань балки, на якій розташовано дві точкові маси m1 = m i m2 = 2m (рис. 18.6,а). Довжина прогону l=3 м. Балка має постійну жорсткість на згин EI=const і нескінченно велику жорсткість на поздовжні деформації: EA= ∞.

18.Метод скінчених елементів в задачах динаміки

Рис.18.6

Дискретну модель балки зображено на рис.18.6,б. У процесі призначення ступнів вільності враховано, що оскільки поздовжня жорсткість балки є нескінченно великою, поздовжні пе-

реміщення вузлів дорівнюватимуть нулю. На кінцях балки розташовано шарнірні опори, тому повороти опорних вузлів не вводяться до складу невідомих вузлових переміщень. Отже, вектор

				r	= { y	y		y	y		} і відповідно
вузлових переміщень має	чотири	компоненти		yT	= { y	y	2	y	y	4	} і відповідно
					1		2	3		4
скінченно-елементна модель − чотири ступні вільності.
Побудуємо матрицю зосереджених мас:
m			m
1
	0			0
M =			=					.			(18.28)
	m2				2m


		0					0

Матриця жорсткості скінченно-елементної моделі матиме такий вигляд:

K		K		K		K
	11,		1,2		1,3		1,4
K2,1		K2,2		K2,3		K2,4
K =								.
K	3,1	K	3,2	K	3,3	K	3,4

		K4,2		K4,3
K4,1						K4,4

18.Метод скінчених елементів в задачах динаміки

При н побудові н матриці н жорсткості н скінченно-елементної н моделі н врахуємо, н що н скінченний

елемент 1-2 має шарнір на початку і затиснення на кінці і належить до третього типу

(див.п.6.6.3), нскінченний нелемент 2-3 нмає нзатиснення на обох кінцях і належить до першого типу

(див.п.6.6.1) н і, нарешті, н скінченний н елемент 3-4 н має н затиснення на н початку н і н шарнір на н кінці н і

належить до другого типу (див.п.6.6.2).

Фізико-геометричні характеристики скінченних елементів занесемо до табл.18.1.

Таблиця.18.1

№ н	П.− к.	l	sinβ	cosβ	EI	i=EI/l

1	1-2	3	0	1	EI	0,3333EI

2	2-3	3	0	1	EI	0,3333EI

3	3-4	3	0	1	EI	0,3333EI

Обчислимо елементи першого стовпця матриці жорсткості. З цією метою надамо вузловому переміщенню y1 одиничне значення (рис.18.7) і обчислимо вузлові реакції.

Рис.18.7

1−2

2−3

1−2

12i

K1,1 = k55

+ k22

=	0	+	3 × 0,3333EI	×12	+	0	+	12 × 0,3333EI	×12	= 0,5555EI ;

		32					32

	3i		1−2			6i	2−3
K2,1	= k651−2 + k322−3 =		C	+	-		C	=
		l				l

3 × 0,3333EI

× 0,3333EI

×1

= -0,3333EI ;

2−3

12i

2−3

12 × 0,3333EI

K3,1 = k52

- fS

= -0 -

×1

= -0,4444EI ;

ето	інчени			е ементів в				а ача		инамі и			13
	2	3
K4,1	6i C			6 0.3333EI				1	0,6666EI.
	l					3
аки	са и чино		,	почер ово надаючи дискретній							оделі одиничні при		усові пере і енн
y2 1, y3	1, y4 1,		о числює			о еле	енти відповідно дру о о, трет о о і четверто о стовпців
атриці жорсткості.		рештою			ає	о
				0,5555				0,3333		0,4444		0,6666
				0,3333				2,3333		0,6666		0,6666
	K		EI									.	(18.29)
				0,4444				0,6666		0,5555		0,3333
				0,6666				0,6666		0,3333		2,3333
Підставивши вира и				.	і	.	у	.	, дістане		о

0,5555

0,3333

0,4444

0,6666

0,3333

2,3333

0,6666

0,4444

0,6666

0,5555

0,3333

0,6666

0,3333

2,3333

а о в координатній фор

0,5555

0,3333a

0,4444a

0,6666a

0,3333a1

2,3333a2

0,6666a3

0,6666a4

(18.30)

0,4444a

0,6666a

0,5555

0,3333a

0,6666a1

0,6666a2

0,3333a3

2,3333a4 0.

ру е і четверте рівн нн

. належат

до фіктивни

дина

ічни

ступнів віл ності.

ци

рівн н

нео ідно вира ити а

плітуди фіктивни

дина ічни

пере

і ен

a2 і a4 та підставити у

перше і третє рівн нн .

о в

уючи су

існо дру е і четверте рівн нн , на оди о

ето інчени е ементів в а ача инамі и 14

a2	0,06667a1			0,26667a3;				(18.31)
a4	0,26667a1			0,06667a3.				(18.31)
a4	0,26667a1			0,06667a3.
Підставл ючи одержані величини у перше і третє рівн нн						фор	ул	. отри ає о
0,3555		a1		0,3111a2			0;	(18.32)
0,1556a1			0,1778			a2	0,	(18.32)
0,1556a1			0,1778			a2	0,
де по начено
			m	2
			EI .					(18.33)
Прирівн вши до нул ви начник	систе и		рівн н		.	, ає	о у	ову на вності віл ни
коливан
0,3555				0,3111
						0,		(18.34)
0,1556			0,1778

відки

0,3555 0,1778 0,3111 0,1556 0;

2 0,5333 0,0148 0,

0,0294,

0,2667 0,2373

0,5040.

нарешті,

на оди о спектр частот власни коливан

0,0294EI	0,1715	EI	,
m		m

0,5040EI	0,7099	EI .
m		m

л ви наченн	оловни	фор коливан відкине о в систе і	(18.32) одне	рівн н ,
наприклад, дру е.	рівн нн ,	о алишилос , підстави о перше власне	число

0,3555 0,0294 a1 0,3111a3 0,

ето

інчени

е ементів в

а ача

инамі и

відки

a3 1,0482a1 ,

то то дл

першо

оловно

фор и,

к о a11

1, то a31

1,0482.

співвідношен

ожна

одержати

a21

0,2128,

a41

0,1968.

Анало ічно о числюют

плітуди пере

ен

дру о

оловно фор

и коливан .

18.8. Змушені коливання при гармонічному навантаженні

ушені коливанн ви начают с диференціал ни

рівн нн

дина

ічно рівнова и (18.14):

K y

P .

л не

о випадок, коли

овнішнє навантаженн

інюєт с

аконо синуса

P Psin t ,

(18.35)

де PT

вектор а плітудни

величин

овнішні

у а ал нени сил.

л даючи процес усталени

коливан , вважати

о,

о коливанн систе

и від увают с

частотою

овнішн о о дина

ічно о навантаженн

y Asin t

2Asin t ,

(18.36)

де AT

A1 A2 An

вектор

плітуд

пере

ен

ушени

коливан .

Післ

підстановки

співвідношен

диференціал не

рівн нн

18.14

ати е о

ал е ра чне рівн нн

2M A

P .

(18.37)

В координатній фор і

атричне рівн нн

на ере ви л ду

18.Метод скінчених елементів в задачах динаміки					16
(K1,1 − m1θ 2 ) A1 +		K1,2 A 2	+K +	K1,n A n	=						1;
								P
K2,1A1	+ (K2,2 − m2θ 2 ) A 2 +K +			K2,n A n	=				2 ;
						P
					(18.38)
L	L	L	L	L	L
Kn,1A1	+	Kn,1A 2	+K + (Kn,n − mnθ 2 ) A n =							n .
							P

Розв’язок алгебраїчних рівнянь визначає амплітуди вузлових переміщень, на базі яких можна визначити кінцеві реакції і, отже, внутрішні зусилля у стержнях системи (див. п. 6.9).

18.9. Приклад розрахунку на змушені коливання

Розрахуємо невагому балку постійної жорсткості EI (рис.18.8,а) з двома точковими масами m1 = m i m2 = 2m на дію вібраційної сили P (t ) = Psinθt . Амплітудна величина сили P=10

кН, циклічна частота θ = 0,8ω1.

Рис.18.8

З розрахунку на вільні коливання перша власна частота

ω		= 0,1715			EI	,
ω	1	= 0,1715			m	,
	1

отже

θ = 0,8ω				= 0,1372			EI	.
θ = 0,8ω			1	= 0,1372				.
			1				m
							m

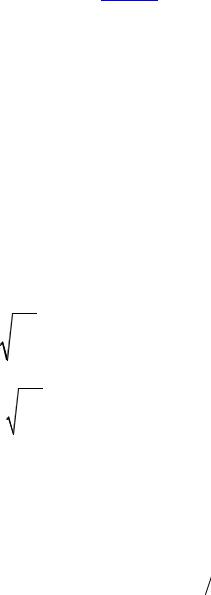
18.Метод скінчених елементів в задачах динаміки

Напрями можливих переміщень мас системи зображено на рис.18.8,б. Матриця мас M і матриця

жорсткості K н скінченно-елементної н моделі н побудовані н в н п.18.7. Вектор амплітуд вузлових

переміщень матиме чотири компоненти:

AT = { A	A	A	A	} .
1	2	3	4

Побудуємо вектор амплітудних величин вузлових динамічних навантажень:

	P			0
		1
r	P			0
		2
P =			=		.
	P3		−10

	P		0
		4

Обчислимо допоміжні величини:

			2
	EI
m1θ2 = m 0,1372					= 0,0188EI ,
	m

				2
		EI
m2θ2 = 2m 0,1372					= 0,0376EI .
		m

Підставимо всі зазначені величини у систему алгебраїчних рівнянь (18.38):

0,5367 A1	−0,3333A 2	−0,4444 A 3	−0,6666 A 4	=	0;
−0,3333A1	+2,3333A 2	+0,6666 A 3	+0,6666 A 4	=	0;
−0,4444 A1	+0,6666 A 2	+0,5179 A 3	+0,3333A 4	= −10 EI ;
−0,6666 A1	+0,6666 A 2	+0,3333A 3	+2,3333A 4	=	0.

Розв’язок системи визначає амплітуди вузлових переміщень:

A =

A		1			−303,020

A		2
A		2	=	1 67,259
						.
						.
A		3		EI −327,975
	A
	A	4			−58,941
		4

18.Метод скінчених елементів в задачах динаміки

Обчислимо зусилля у скінченному елементі 1-2 (S=0, C=1, l=3м, i=EI/3).

Побудуємо вектор кінцевих переміщень для стержня 1-2 (позначення і напрями кінцевих пере-

міщень наведено на рис.18.9,а,б):

									Рис.18.9
						d				0						0
							1
						d2				0				1		0
					r	d			0					1		0
					δ	= 3 =					=						.
					δ	= 3 =					=						.
					1−2	d4			0				EI			0
						d			A						-303,02
							5			1
						d6			A2						67,259
Обчислимо кінцеві реакції у стержні за формулою
								r	= k¢			T			δ	.							(18.39)
								s¢	= k¢			T			δ	.							(18.39)
								1−2			1−2 1−2 1−2
Вигляд матриці жорсткості k′						для стержня третього типу (шарнір на початку і затиснення на
кінці стержня) наведено в п.п.6.5.3. Отже:
	0	0		0 0		0					0			1 0			0 0 0 0					0
						-0.1111
	0	0,1111		0	0	-0.1111				-0.3333					0	1	0	0	0	0		0
r	0	0		0 0		0					0 0 0						1 0 0 0					0		,
s¢	=													×						×				,
1−2	=													×						×
	0	0		0 0		0					0			0 0			0 1 0 0					0
	0	-0,1111		0	0	0,1111				0,3333					0	0	0	0	1	0	-303,02
		-0,3333
	0	-0,3333		0	0	0,3333					1				0	0	0	0	0	1	67,259
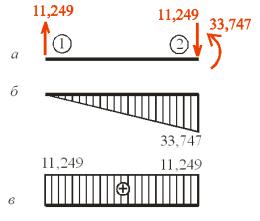
		r′	T	= {0		11,249				0		0			−11,249			−33,747}.
		(s1−2 )		= {0		11,249				0		0			−11,249			−33,747}.

На рис.18.10,а зображені сумарні кінцеві реакції, на рис.18.10,б − епюра згинаючих моментів,

а на рис.18.10,в − епюра поперечних сил у скінченному елементі 1-2.

18.Метод скінчених елементів в задачах динаміки

Рис.18.10

Аналогічно можна побудувати епюри внутрішніх зусиль в скінченних елементах 2-3 і 3-4.

Потрібно лише мати на увазі, що скінченний елемент 2-3 належить до першого, а скінченний елемент 3-4 − до другого типу, і вживати відповідні цим типам матриці жорсткості.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>