
- •Зміст підручника
- •1. Вступ
- •3. Теорія переміщень
- •8. Ферми
- •9. Тришарнірні арки
- •10. Плоскі рами
- •11. Метод сил
- •12. Метод переміщень
- •13. Змішаний метод
- •V.ОСНОВИ ДИНАМІКИ І СТІЙКОСТІ СПОРУД
- •17. Коливання систем із нескінченно великим числом ступнів вільності
- •18. Метод скінченних елементів у задачах динаміки
- •19.Стійкість споруд
- •23. Статично визначувані ферми
- •24. Розпірні системи
- •26. Нерозрізні балки
- •VIII. НАВЧАЛЬНІ ПРОГРАМНІ КОМПЛЕКСИ
- •27. Навчальний програмний комплекс АСИСТЕНТ
- •28. Комп’ютерне самотестування рівня знань

ДО ЗМІСТУ ПІДРУЧНИКА
1.Вступ
Зм і с т г л а в и
1.1.Задачі будівельної механіки
1.2.Основні припущення будівельної механіки
1.3. Навантаження
1.4. Розрахункові схеми споруд
1.5. Короткий історичний огляд
1.1.Задачі будівельної механіки
Усі інженерні конструкції і споруди − будівлі, мости, башти, резервуари, корпуси машин,
літаків, суден, ракет тощо − повинні задовольняти умовам міцності, жорсткості і стійкості.
Умови міцності полягають в тому, що внутрішні зусилля і напруження в елементах конструкцій не повинні перевищувати величин, за яких ці елементи можуть зруйнуватися.
В процесі експлуатації на конструкції і споруди діють зовнішні навантаження і впливи,
внаслідок чого їхні елементи деформуються і набувають деяких переміщень у просторі. Ці переміщення можуть спотворити зовнішній вигляд споруди або взагалі зробити її непридатною до експлуатації. Перевірка умов жорсткості − це порівняння деформацій споруди з тими, що припускаються.
Окрім основних навантажень, які можуть бути передбачені заздалегідь, на конструкцію або споруду можуть діяти інші непрогнозовані навантаження. Вони носять випадковий характер і мають незначну величину, проте викликають деякі додаткові деформації і переміщення. При знятті цих додаткових навантажень споруда має поновлювати свій попередній стан. Це є умовою стійкості споруди. До цих умов слід ще додати умови економічності: споруда мусить відповідати умовам міцності, жорсткості і стійкості при забезпеченні мінімальної власної ваги, а отже,
мінімальної вартості.

1.Вступ |
2 |
|
|
Виконання зазначених умов повинно передбачатися в процесі проектування конструкцій або споруд, тобто під час розрахунку їх на зовнішні впливи і навантаження. Будівельна механіка −
це наука, що розробляє методи розрахунку інженерних конструкцій і споруд на міцність,
жорсткість і стійкість.
З огляду на викладене сформулюємо основні завдання, що стоять перед будівельною
механікою:
1.Дослідження та утворення раціональних форм споруд.
2.Обчислення внутрішніх зусиль в усіх елементах конструкції або споруди, тобто визначення напруженого стану об’єкта, що вивчається.
3.Аналіз переміщень, які виникають в споруді (дослідження деформованого стану) під зов-
нішніми діями
4.Дослідження стійкості споруди.
Напруження, деформації і переміщення, які виникають у тілах різного виду від зовнішніх
навантажень, вивчаються в механіці твердого деформівного тіла. Розділами цієї науки є опір
матеріалів, теорія пружності, теорія пластичності, теорія повзучості, будівельна механіка.
Опір матеріалів займається розрахунками окремого пружного тіла, як правило, стержня або балки. Теорія пружності, теорія пластичності, теорія повзучості вирішують те саме завдання, що й опір матеріалів, але на вищому математичному рівні з використанням меншої кількості вихід-
них гіпотез, що дозволяє, з одного боку, оцінити розв’язки, які отримані за методами опору матеріалів, з іншого - знайти розв’язки нових задач, які взагалі не можуть бути вирішені методами опору матеріалів.
Будь-яка споруда складається з елементів, які за співвідношенням геометричних розмірів умовно можуть бути віднесені до масивних тіл, тонкостінних елементів - пластин і оболонок,
стержнів, тонкостінних стержнів (рис.1.1).
Рис.1.1

1.Вступ |
3 |
|
|
До масивних відносять просторові елементи, розміри яких в усіх трьох вимірах є величинами одного порядку (рис.1.1,а), у пластині (рис.1.1,б) і оболонці (рис.1.1,в) один із розмірів (товщина h) набагато менше двох інших a і b, у стержні (рис.1.1,г) два розміри –ширина a і висота h
набагато менші за його довжину b, у тонкостінному стержні (рис.1.1,д) ці три розміри мають різний порядок.
Таким чином, опір матеріалів розглядає задачі розрахунку окремих стержнів, до яких, як правило, належить й створена протягом останніх десятиліть теорія тонкостінних стержнів.
Задачі розрахунку інших елементів розглядаються теорією пружності, теорією пластичності,
теорією повзучості відповідно до врахування реальних властивостей матеріалу тіла.
Будівельна механіка вивчає складні механічні системи, до яких входять елементи різних типів: масивні тіла, пластини, оболонки, стержні.
Таке визначення будівельної механіки остаточно склалося в останні десятиріччя, оскільки стало можливим поряд із постановкою задачі дати методи, математичний апарат і програмне забезпечення для її розв’язання. Раніше таке визначення традиційно пов’язувалось із поняттям будівельної механіки в широкому розумінні і трактувалось як сукупність окремих дисциплін, які займаються розрахунком споруд. При цьому будівельна механіка у вузькому розумінні розгля-
дала складені зі стержнів механічні системи, які називаються стержневими системами. До стержневих систем можуть бути віднесені ферми (рис.1.2,а), балки (рис.1.2,б), рами (рис.1.2,в),
арки (рис.1.2,г) та комбіновані системи (рис.1.2,д), які утворюються поєднанням балок, рам або арок з фермами.
Рис.1.2
Цей розділ нині найширше відображений у навчальній літературі і носить назву будівельної механіки стержневих систем. Протягом довгого часу він називався “ статикою споруд”, “ графіч-
ною статикою споруд” тощо.
Зазначимо, що для формулювання задачі будівельної механіки необхідні характеристики механічної моделі конструкції, властивостей матеріалу тіла, навантаження.
Будівельна механіка має характерні особливості.
1.Вступ |
4 |
|
|
Насамперед, вона спрямована на задачі проектування конструкцій, і тому, на відміну від інших розділів механіки, на кінцевому етапі передбачає одержання числового результату. Історія розвитку будівельної механіки відображає розвиток математичних методів і засобів обчислювальної техніки; саме останні, як правило, визначають можливості у постановці задач будівельної механіки та їхньої реалізації.
Будівельна механіка розв’язує задачу визначення напружено-деформованого стану системи під дією навантажень, які вважаються заданими, тобто, як правило, задача взаємодії фізичних полів не розв’язується.
Поряд з теоретичними будівельна механіка традиційно включає в себе й експериментальні методи, проте в даний час вони викладаються в спеціальних курсах – таких, як
“ Експериментальні методи”, “ Випробування споруд” тощо.
Будівельна механіка обмежується визначенням напружень, деформацій і переміщень під дією зовнішніх навантажень і не формулює критерії міцності, як це робиться в опорі матеріалів. Буді-
вельна механіка стержневих систем на відміну від опору матеріалів, вивчає не напруження і деформації в окремих перерізах елементів, а їхні інтегральні характеристики − зусилля.
1.2.Основні припущення будівельної механіки
Розрахунки в будівельній механіці базуються на деяких припущеннях. Вони, як правило,
збігаються з припущеннями, які мають місце в опорі матеріалів і в теорії пружності, але відносяться до всієї споруди в цілому.
∙Гіпотеза суцільності − тіло вважається суцільним, таким, що неперервне заповнює свій об’єм. На цій підставі деформації і переміщення точок елемента можуть вважатися неперер-
вними функціями координат.
∙Гіпотеза однорідності та ізотропності: властивості матеріалу однакові в усіх точках і по усіх напрямках.
∙Гіпотеза ідеальної пружності: матеріал конструкцій вважається ідеально пружним. Це означає, що після зняття навантаження деформація усувається, споруда сповна поновлює фор-
му, яку мала до початку навантаження і повертає енергію, яку було витрачено на її деформацію.
∙Гіпотеза лінійної залежності між деформаціями і напруженнями: вважається, що між напруженнями і деформаціями в усіх точках зберігається лінійна залежність (закон Гука).
Завдяки цій гіпотезі, разом з попередніми, пружні властивості матеріалу в усіх точках тіла

1.Вступ |
5 |
|
|
характеризуються трьома параметрами: модулем пружності E, модулем зсуву G і коефіцієнтом Пуассона ν, які пов’язані між собою залежністю G = E 2(1 + ν) .
2(1 + ν) .
∙Гіпотеза малих переміщень: переміщення точок системи, які зумовлені пружними деформа-
ціями, є малими, тобто такими, що допускають лінійну залежність між деформаціями і перемі-
щеннями в рівняннях геометричного аспекту задачі, а також складання рівнянь рівноваги для недеформованого стану.
Рис.1.3
Наприклад, якщо елемент AB (рис.1.3) після деформації займає положення A′B′ , то лінійна деформація εx може бути обчислена в такий спосіб:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ ′ |
− AB |
|
|
|
|
|
|
(dx + u + du − u )2 |
+ (w + dw − w)2 − dx |
|
||||||||||||||||||||||||||
ε |
|
= |
A B |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
du 2 |
|
|
dw 2 |
|
|
|
|
|
|
du |
du 2 |
|
dw 2 |
|
||||||||||||||||||||||
= |
|
|
1 |
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
−1 = |
|
1 + 2 |
|
+ |
|
|
|
|
+ |
|
|
−1 ≈ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
dx |
|
|
dx |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
du |
|
|
|
1 du 2 |
|
1 |
dw 2 |
|
du |
|
1 dw 2 |
|
|||||||||||||||||||||
|
|
|
|
≈ 1 + |
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
− |
1 ≈ |
|
|
|
+ |
|
|
|
|
. |
|
|||||||||
|
|
|
|
|
dx |
|
|
|
|
|
2 |
|
|
dx |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 dx |
|
|
|
dx |
|
|
2 dx |
|
||||||||||||||||||||||
Якщо переміщення малі, такі, що
1 |
dw 2 |
du |
||||
|
|
|
|
<< |
|
, |
|
|
|
||||
2 |
|
dx |
|
dx |
||
то
εx = du dx
ізалежність між деформацією εx і переміщенням u є лінійною.
Вопорі матеріалів при розгляді елементарної теорії згину балок гіпотеза малих переміщень дозволяє точне рівняння осі балки при згині
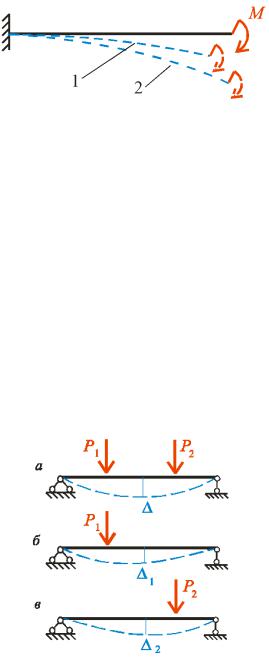
1.Вступ |
6 |
|
|
|
|
1 |
= − |
M |
|
(1.1) |
||
|
|
|
EI |
|||||
|
|
ρ |
|
|||||
замінити наближеним |
|
|
|
|
||||
|
d 2w |
= − |
M |
(1.2) |
||||
|
|
EI |
||||||
|
|
dx2 |
|
|
||||
і, наприклад, консольна балка, зображена на рис.1.4, при постійному по довжині згинальному моменті, що повинна була б при сталій кривизні згинатися по дузі кола 1 (як це випливає з рівняння), за елементарною теорією згинається по параболі 2, рівняння якої є розв’язком рівнян-
ня (1.2).
Рис.1.4
∙Гіпотеза природного ненапруженого стану: початкові напруження в тілі вважаються такими, що дорівнюють нулю. Це означає, що напруження і зусилля, які визначаються в результаті розрахунку, становлять лише їхній приріст над тими, що були спочатку.
Із наведених гіпотез випливає принцип незалежності дії сил (принцип суперпозиції): в
лінійно деформівних системах сумарний ефект від дії кількох сил дорівнює сумі ефектів від дії кожної сили окремо. Причому сумарний ефект не залежить від порядку їхнього прикладення.
Під ефектом слід розуміти переміщення точок споруди, опорні реакції, зусилля, напруження тощо. Так, позначимо через прогин будь-якої точки балки, на яку діють дві зосереджені сили
(рис.1.5,а). Прогин цієї точки, що зумовлений силою P1, позначено 1 (рис.1.5,б), а прогин від дії сили P2 (рис.1.5,в) − 2.
Рис.1.5
1.Вступ |
7 |
|
|
Тоді можна сказати, що |
|
= 1 + 2 . |
(1.3) |
Принцип суперпозиції (1.3) дає змогу розкласти розв’язання задачі при складних навантаженнях на розв’язання кількох окремих задач при простих навантаженнях. Цей принцип може бути застосований для побудови епюр зусиль або прогинів, де він іноді називається
принципом накладання.
При розв’язанні задач опору матеріалів і будівельної механіки велике значення має принцип Сен-Венана: якщо до будь-якої малої частини споруди прикладено зрівноважену систему сил, то вона викликає напруження, які швидко зменшуються в міру віддалення від цієї частини. Іншими словами: в точках, які є віддаленими від місця прикладання зовнішнього навантаження, напру-
ження мало залежать від детального способу реалізації цього навантаження. Принцип Сен-
Венана широко застосовується у будівельній механіці і дозволяє переносити сили по лінії їхньої дії, замінювати розподілені навантаження зосередженими силами (або навпаки) і вважати при цьому, що напруження і деформації у перерізах, достатньо віддалених від місця навантаження,
практично не змінюються. За такого формулювання принцип Сен-Венана називають принципом
пружної рівнозначності статично еквівалентних систем сил.
Додатково до вказаних гіпотез і принципів при розгляді конкретних систем будівельна механіка допускає різні гіпотези прикладної теорії пружності, наприклад, гіпотезу Кірхгофа– Лява для пластин і оболонок. Будівельна механіка стержневих систем досліджує системи,
елементом яких є стержень, при цьому використовуються додатково основні гіпотези опору матеріалів, наприклад, гіпотези елементарної теорії згину балок і т. д.
Не всі з наведених вище гіпотез повинні виконуватися одночасно. Наприклад, можна уявити собі що розглядається система, в якій очікуються не малі переміщення і треба відмовитися від відповідної гіпотези. Тоді ми отримаємо геометрично нелінійну задачу, де вже не виконується принцип суперпозиції. Можна уявити собі й інші умови для задач будівельної механіки (фізично нелінійні задачі), де відкидається гіпотеза лінійної залежності між деформаціями і напруженнями, задачі де нехтується гіпотеза однорідності та ізотропності тощо. Такі задачі виникають у практиці, але у цьому підручнику, який має характер першочергового і базового,
вони не розглядаються.
1.3. Навантаження
Методи розрахунку конструкцій великою мірою залежать від характеру зовнішнього навантаження, способу його прикладання, а також від умов роботи споруди. Поняття
|
т п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
навантаженн , |
окрі |
|
овнішні |
|
сил, |
поширюєт с |
на такі ді , |
к вплив |
те пературни |
а о |
||||||||||||||||||||||||
електро |
а нітни |
випро |
інюван , |
при усове |
і |
енн |
опор а о окре и |
|
ву лів конструкцій, |
|||||||||||||||||||||||||
попереднє |
напруженн |
|
то |
о. |
|
алежно від поведінки у часі |
навантаженн |
|
ожут |
|
ути |
|||||||||||||||||||||||
ро поділені на статичні й дина |
ічні. |
о статични |
|
ожут |
ути віднесені такі навантаженн , |
кі |
||||||||||||||||||||||||||||
інюют с |
в часі |
не начною швидкістю, |
коли прискоренн |
и |
ас систе |
и, |
о |
у |
овлені |
|||||||||||||||||||||||||
дефор |
аці |
|
и, |
|
ожна |
|
не тувати. |
авантаженн , |
ке |
у |
овлює |
начні |
прискоренн |
|
ас |
|||||||||||||||||||
споруди, внаслідок чо о |
еле енти починают коливатис , на иваєт с |
дина |
ічни . |
|
|
|
|
|
||||||||||||||||||||||||||
алежно від спосо у прикладанн |
ро рі н ют |
навантаженн |
осереджені |
і |
ро поділені. |
|||||||||||||||||||||||||||||
еал ні навантаженн |
авжди є ро поділени |
и. |
о |
осереджени |
віднос т |
|
такі навантаженн , |
|||||||||||||||||||||||||||
кі передают с |
на споруду на невеликій по відношенню до |
ро |
ірів пло |
|
і, |
ку |
ожна у |
овно |
||||||||||||||||||||||||||
прийн ти а точку. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
овнішні |
ді |
поділ ют с |
на |
постійні |
і |
ти |
часові. |
Постійне |
навантаженн |
діє |
впродовж |
|||||||||||||||||||||||
вс о о тер |
іну існуванн |
споруди |
е |
іни |
ісц |
|
прикладанн , величини та напр |
ку. |
к пра- |
|||||||||||||||||||||||||
вило, |
до |
постійно о |
|
навантаженн |
віднос т |
|
власну |
ва у |
споруди. |
о |
ти |
часово о |
||||||||||||||||||||||
дов отер |
іново о навантаженн |
|
|
ожна віднести ва у де ки |
еле |
ентів споруди, |
кі прот |
о |
||||||||||||||||||||||||||
часу |
ожут |
|
|
інювати сво |
арактеристики |
ро ташуванн , величину то |
о. Прикладо |
тако о |
||||||||||||||||||||||||||
навантаженн |
|
оже ути ва а стаціонарно о о ладнанн . |
о короткотер |
іново о ти |
часово о |
|||||||||||||||||||||||||||||
навантаженн |
віднос т |
сні ове і вітрове навантаженн , ва у людей, те |
пературні ді |
то |
о. |
|
|
|
||||||||||||||||||||||||||
авантаженн |
також |
ожут |
поділ тис |
|
а спосо о |
ді . |
ак, однопара |
|
етрични |
вважают |
||||||||||||||||||||||||
таке навантаженн , |
всі складові |
ко о |
інюют с |
в часі пропорційно одно |
у пара |
етру. |
к |
|
о |
|||||||||||||||||||||||||
систе |
а |
овнішні |
сил |
|
оже |
ути ро |
ита на окре |
і |
рупи, кожна |
ки не |
алежит від інши , |
|||||||||||||||||||||||
таке навантаженн |
|
на ивают |
а атопара |
етрични |
. |
авантаженн , |
ке |
|
інює своє ро ташу- |
|||||||||||||||||||||||||
ванн |
на споруді, на ивают |
ру о |
|
и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.4. |
озрахункові схеми споруд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
При ро ра унку споруд на |
іцніст , жорсткіст |
і стійкіст |
вичайно ро |
|
л дают |
не реал ну |
||||||||||||||||||||||||||||
споруду, а |
|
спро |
ену с е у, |
ка на иваєт с |
ро ра унковою. |
е пов |
ано |
|
ти |
, |
о еле |
енти, |
||||||||||||||||||||||
ки |
|
складаєт с |
|
іл шіст |
|
споруд, |
ают |
|
складну |
структуру. |
о |
у дл |
ро ра унку |
|||||||||||||||||||||
доводит с |
спро |
увати систе |
у, |
|
о ро ра овуєт с , свідо |
о від |
овл ючис |
від де ки |
|
енш |
||||||||||||||||||||||||
суттєви |
факторів. |
Отже, розрахункова схема |
|
це спро |
ене о раженн |
|
споруди, |
ке одер- |
||||||||||||||||||||||||||
жуєт с |
а ра унок і норуванн |
дру ор дни |
факторів. Пере ід від реал но споруди до |
ро ра- |
||||||||||||||||||||||||||||||
унково с е |
и – дуже відповідал ний етап ро ра унку. По-перше, спро |
енн , |
кі внесені при |
|||||||||||||||||||||||||||||||
1.Вступ |
9 |
|
|
переході до розрахункової схеми, повинні зробити прийнятною трудомісткість розрахунку, між тим, по-друге, вони повинні забезпечити достовірність результатів.
Загальних рекомендацій щодо переходу від реальної споруди до розрахункової схеми немає.
Проте існують деякі типові прийоми, які можуть бути проілюстровані на наступному прикладі.
Залізобетонну балку довжиною L покладено на дві стіни (рис.1.6,а). Відстань між осями стін позначено lc . Відстань між внутрішніми поверхнями стін (прогін “ у світлі”) - l0 . На балці розташоване обладнання вагою Q. Балка має прямокутний переріз (рис.1.6,б) висотою h і ши-
риною b. Замінимо цю конструкцію розрахунковою схемою. Балка спирається на стіни по деяких площадках довжиною ( L − l0 ) 2 . Ці реальні опори замінюються ідеалізованими опорами, одну з яких беруть за шарнірно-нерухому, а другу - за шарнірно-рухому. Розташову-
2 . Ці реальні опори замінюються ідеалізованими опорами, одну з яких беруть за шарнірно-нерухому, а другу - за шарнірно-рухому. Розташову-
ються ці уявні опори в центрах площадок спирання.
Реальні балки завжди мають дефекти виготовлення: деякі незначні відхилення від проектних розмірів, порушення прямолінійності ребер тощо. Вважаючи, що зазначені відхилення мало впливають на розподіл напружень в перерізах балки, знехтуємо цими дефектами, так само як і можливою нерівномірністю розподілу щебеня, можливим відхиленням в якості бетону тощо і за-
мінимо реальний брус відрізком прямої довжиною l = L - 2 ×(L - l0 ) 4 = ( L + l0 )
4 = ( L + l0 ) 2 , який збі-
2 , який збі-
гається з віссю реального бруса. Матеріал цієї уявної балки схарактеризуємо модулем пружності
E, коефіцієнтом Пуассона n та об’ємною вагою g. Параметри, що визначають жорскісні харак-
теристики розрахункової схеми, залежать від форми поперечного перерізу. Для прямокутного перерізу маємо: площа A = bh , момент інерції I = bh3 12 .
12 .

1.Вступ |
10 |
|
|
Рис.1.6
Вагу Q реального обладнання умовно замінимо або рівномірно розподіленим навантажен-
ням (рис.1.6,в) інтенсивністю q = Q a , або зосередженою силою P=Q, що прикладена в середині бази a. Власну вагу G = lbhγ балки можемо врахувати як рівномірно розподілене навантаження інтенсивністю g = G
a , або зосередженою силою P=Q, що прикладена в середині бази a. Власну вагу G = lbhγ балки можемо врахувати як рівномірно розподілене навантаження інтенсивністю g = G l = bhγ (рис.1.6,д) або можемо знехтувати нею, якщо власна вага набагато менша за вагу обладнання.
l = bhγ (рис.1.6,д) або можемо знехтувати нею, якщо власна вага набагато менша за вагу обладнання.
Таким чином, реальну балку (рис.1.6,а) зведено до розрахункових схем (рис.1.6,в – 1.6, д). Для цієї схеми можна обчислити опорні реакції, побудувати епюри внутрішніх зусиль і прогинів.
Наприкінці від розрахункової схеми необхідно повернутися до первісної конструкції, обчислити нормальні і дотичні напруження в її волокнах і зіставити з напруженнями, які може витримати матеріал, з якого виготовлено балку.
Для прикладу наведемо складніші розрахункові схеми будівельних споруд: поперечник головного корпуса ТЕЦ (рис.1.7,а) і просторовий рамний каркас будівлі (рис.1.7,б).

1.Вступ |
11 |
|
|
Рис.1.7
Конструкції, які утворюють споруду, є складними механічними системами. Задача розрахунку споруди, сформульована за допомогою відповідних математичних рівнянь,
залежностей або умов, є математичною моделлю розрахунку споруди.
Розрізняють дискретний, континуальний і дискретно-континуальний методи формулювання математичної моделі розрахунку споруди. Якщо стан системи характеризується скінченним чис-
лом параметрів, наприклад компонентів переміщень вузлів ферми, рами, або зусиль у стержнях,
то модель називають дискретною. Такі моделі описуються системами алгебраїчних рівнянь стосовно невідомих параметрів. У випадку, коли стан системи характеризується функціями однієї, двох або трьох змінних, тобто нескінченно великим числом параметрів − значень цих функцій, модель називається континуальною. При цьому розрізняють одновимірну (стержень),
двовимірну (пластина, оболонка), тривимірну (масивне тіло) задачу. Математична модель континуальної системи описується функціональними рівняннями (диференціальними − зви-
чайними для одновимірної задачі або у частинних похідних для дво- і тривимірної задачі,
інтегральними або інтегро-диференціальними рівняннями). Комбіноване використання двох зазначених моделей утворює дискретно-континуальну модель.
Термінологія, що пов’язана з методами формулювання математичної моделі, інколи переноситься й на самі системи і відповідно розрізняються дискретні, континуальні та дис-
кретно-континуальні системи.
Слід зауважити, що наведений поділ є умовним, оскільки сучасна будівельна механіка розглядає складні механічні системи, які описуються моделями, що включають різні типи рівнянь і, як правило, не допускають аналітичних розв’язків, дискретизуються безпосередньо у процесі розв’язання за допомогою різних чисельних методів. Таким чином, існує поняття
наближеної математичної моделі розрахунку споруди, якій часто можна поставити у відповідність реальну фізичну дискретну модель споруди, що фактично розраховується. При цьому питання відповідності, тобто ступеня точності розрахунку, розв’язується, як правило, на

1.Вступ |
12 |
|
|
фізичному рівні точності (якщо не вдається дати строгих математичних оцінок) шляхом порівняння результатів розрахунку схем із різним рівнем дискретизації.
У методі скінченних елементів система, що розраховується, замінюється її дискретною моделлю, яка утворюється розбивкою схеми на окремі елементи скінченних розмірів, котрі поєд-
нуються поміж собою в окремих точках, що називаються вузлами. Отже, розрахункова схема матиме вигляд сукупності скінченних елементів, на які розділено вихідну систему.
Так, на рис.1.8,а зображено розбивку на скінченні елементи ротора газової турбіни, на рис.1.8,б − корпуса ядерного реактора, а на рис.1.8,в − корпуса літака.
Рис.1.8
Таким чином, у процесі розрахунку будь-якої конструкції або споруди завжди можна виділити три етапи:
1.ідеалізація, яка полягає в переході до розрахункової схеми;
2.аналіз − власне розрахунок ідеалізованої розрахункової схеми;
3.інтерпретація − перенесення результатів розрахунку до вихідної схеми, висновки щодо
реальної конструкції.
При розв’язанні задач будівельної механіки розрахункова схема вважається заданою. Отже,
перший етап із розрахунку усувається. Разом із тим у процесі розв’язання слід пам’ятати, що цей етап існує і що розрахункова схема, яка розглядається, отримана в результаті нехтування рядом особливостей реального об’єкта. Як наслідок, аналіз розрахункової схеми доцільно провадити в межах такої самої точності, яка вже закладена вибором розрахункової схеми.
1.Вступ |
13 |
|
|
У будівельній механіці не розглядається і третій етап розрахунку, а також не вирішуються питання вибору параметрів перерізів, конструювання елементів. Означені питання викладаються у спеціальних курсах конструкцій.
Слід зауважити таке: відмова від аналізу першого і третього етапів розрахунку не значить, що будівельна механіка не має до них жодного відношення. І не тільки тому, що напружено-
деформований стан залежить від тих гіпотез, якими ми скористувалися, а можливість використання результатів рішення задачі при оцінці поведінки реальної конструкції залежать від того, наскільки детально ми можемо розв’язати задачу у рамках будівельної механіки. Треба брати до уваги й те, що сама будівельна механіка розвивається під впливом розвитку дисциплін,
що лежать у основі першого і третього етапів, а також самі ці дисципліни міняються залежно від можливостей, які надаються будівельною механікою
Якщо простежити за еволюцією будівельної механіки в останні п’ятдесят років, можна виявити стійку тенденцію переходу від розв’язання задач суто будівельного профілю до більш загального − машинобудівного. Між тим сам термін “ будівельна механіка” склався історично і,
на жаль, допускає її вузьке розуміння і віднесення до будівельної галузі, що призводить, зокрема,
до викладання класичних курсів будівельної механіки стержневих систем переважно для будівельних або пов’язаних із будівництвом спеціальностей, відносного скорочення розділів стійкості і динаміки споруд і т.п. До речі, англійський термін “structural mechanics” у перекладі означає “ механіка конструкцій”, “ механіка структур”, “ структурна механіка”. Така трактовка є більш точною, оскільки передбачає застосування до конструкцій, які зустрічаються не тільки і навіть не стільки в галузі будівництва, скільки у різних галузях техніки, зокрема у машино-,
судно-, ракетобудуванні, космічній техніці тощо. Сучасна будівельна механіка розглядає задачі з параметрами, характерними саме для цих галузей.
Різноманітність і специфічні особливості розрахункових схем у різних галузях техніки, а
також відсутність у свій час загальних підходів привели до виникнення цілого спектру дисциплін, які розглядають задачі будівельної механіки для об’єктів із різними параметрами – таких, як будівельна механіка літака, будівельна механіка літальних апаратів, будівельна механіка ракет, будівельна механіка корабля тощо, а також будівельна механіка оболонок,
будівельна механіка металевих конструкцій тощо. Справа, звичайно, не в термінології, а у її правильному використанні відповідно до змісту при вирішенні питань організації наукових досліджень і навчального процесу з будівельної механіки.
1.Вступ |
14 |
|
|
1.5. Короткий історичний огляд
Будівельна механіка як наука про деформівні системи народилась у далекому минулому в зв’язку із потребами людини і має багатовікову історію, яку описано у численних книжках і оглядах [16,26]. Характерно, що розвиток будівельної механіки йшов шляхом удосконалення постановок задач і методів їхнього розв’язання і пов’язаний не тільки з потребами виробництва,
зокрема таких галузей, як будівництво, машинобудування, а і з розвитком математичних методів і засобів обчислювальної техніки.
Прийнято вважати, що система знань про міцність почала складатись у ХV−ХVІІст. у працях Леонардо да Вінчі (1452−1519), Галілео Галілея (1564−1642), Роберта Гука (1635−1703), Е.Марі-
отта (1620−1684) та ін. Подальший її розвиток пов’язаний з іменами Я.Бернуллі (1654−1705),
Л.Ейлера (1707−1783), Ж.Лагранжа (1736−1813), М.В.Ломоносова (1711−1765), І.П.Кулібіна
(1735−1818), який, зокрема, розробив проект і створив модель аркового моста через р.Неву прогоном 300 м. Розробці графічних методів розрахунку споруд присвячені праці Ш.О.Кулона
(1736−1806), К.Кульмана (1821−1881), Л.Кремони (1830-1903).
Зазначимо, що на цьому етапі розвитку будівельної механіки через недосконалість обчислювальних засобів користувалися переважно графічними методами, а з появою арифмометрів почали застосовуватись аналітичні підходи. При цьому проблема полягала переважно у розв’язанні систем алгебраїчних рівнянь, і зусилля дослідників спрямовувались, з
одного боку, на розвиток наближених методів, які дозволяли б знизити порядок системи рівнянь,
а з іншого − на розробку спеціальних прийомів розв’язання системи рівнянь.
Можна вважати, що будівельна механіка як наука відбрунькувалась із загальної механіки у другій половині ХІХ століття. На той час головними об’єктами її вивчення були стержневі конструкції, зокрема ферми мостів. Наприкінці ХІХ і на початку ХХ ст. з розвитком техніки значно ускладнилися схеми стержневих і нестержневих систем. У розрахунках дедалі частіше почали застосовуватись методи теорії пружності, теорії пластичності. Поряд із розрахунками статично визначуваних конструкцій розвивались методи розрахунку статично невизначуваних систем.
Принципові положення у розвиток будівельної механіки внесені Л.Нав’є (1785−1836), який замість вивчення руйнування споруд запропонував розглядати їхній робочий стан, тобто пружну стадію роботи [16]. Працями Л.Нав’є, О.Коші (1789−1857), Б.Сен-Венана (1797−1886) за-
вершилось формування основних рівнянь теорії пружності. На цей час сформувалися фундаментальні варіаційні принципи будівельної механіки − принцип Ж.Лагранжа і принцип А.Кастільяно (1847−1884).
1.Вступ |
15 |
|
|
Розвиток будівельної механіки в той період пов’язаний з іменами Б.П.Клапейрона
(1799−1864), Г.Ламе (1795−1870), Дж.Максвелла (1831−1879), О.Мора (1835−1918), Д.Релея
(1842−1919), С.П.Тимошенка (1878−1972) та ін. У 1857 р. Б.П.Клапейроном було запропоновано рівняння трьох моментів для розрахунку нерозрізних балок. У 1864 р. Дж.Максвеллом і в 1876 р.
О.Мором була отримана формула для визначення переміщень у пружних системах за заданими внутрішніми зусиллями, що надала можливість зручного розрахунку статично невизначуваних систем.
Значну роль відіграли праці Д.І.Журавського (1821−1891), Х.С.Головіна (1844−1904),
М.А.Белелюбського (1845−1922), Ф.С.Ясинського (1856−1899), В.Г.Шухова (1853−1939),
Л.Д.Проскурякова (1858−1926), І.П.Прокоф’єва (1877−1958), які внесли суттєвий вклад у роз-
робку методів розрахунку і проектування мостів та інших споруд.
Розвитку методів будівельної механіки та їхньої інтеграції з методами теорії пружності сприяли фундаментальні праці В.Рітца (1878−1909), І.Г.Бубнова (1872−1919), Б.Г.Гальоркіна
(1871−1945), О.М.Крилова (1863−1945), М.І.Мусхелішвілі (1891−1976), П.Ф.Папковича
(1887−1946), а також В.З.Власова (1906−1958), який, зокрема, завершив створення загальної теорії тонкостінних стержнів.
Лише у 30-х роках нашого століття набули завершеної форми методи розрахунку статично невизначуваних стержневих систем, виділені методи сил, переміщень і змішаний метод, а також різні їхні модифікації. У процес їхнього формування значний внесок зробили В.Л.Кирпичов,
М.С.Стрелецький, О.О.Гвоздєв, П.Л.Пастернак, І.М.Рабінович, М.І.Безухов, В.В.Болотін та ін.
Поряд із удосконаленням методів розрахунку конструкцій на міцність виникла необхідність їхньої перевірки на стійкість. Незважаючи на те, що постановка проблеми і перший розв’язок задачі стійкості стисненого стержня належить Л.Ейлеру (1757 р.), розрахунки на стійкість почали широко застосовуватись тільки на початку ХХ ст. Суттєвий внесок у вирішення проблеми внесли Ф.Енгессер, Ф.С. Ясинський, С.П.Тимошенко та інші. Були отримані розв’язки задач стійкості арок, стиснених пластин, оболонок. В 1904 р. С.П.Тимошенко розв’язав задачу стійкості плоскої форми згину двотаврових балок. Узагальнення цієї задачі на тонкостінні стержні зроблено В.З.Власовим. М.В.Корноуховим у 1937 р. запропонований метод розрахунку рам на стійкість, який є узагальненням методу переміщень. На початку ХХ століття задачі стійкості були поширені на конструкції, які працюють за межею пружності (С.Ф.Енгессер,
Т.Карман, Ф.Р.Шенлі), а також на системи, де необхідно враховувати повзучість (О.Р.Ржаніцин).
Наявність у період до середини ХХ ст. малопотужних обчислювальних засобів зумовила розвиток лише простих і наближених методів розрахунку, використання розрахункових схем з
1.Вступ |
16 |
|
|
невеликою кількістю ступнів вільності, переважне використання статичних постановок задач,
що стримувало прогрес у будівництві, машино-, ракето-, авіабудуванні, космічній техніці.
Бурхливий розвиток обчислювальної техніки впродовж останніх десятиріч, перехід до повної автоматизації розрахунків, привели до докорінних змін у постановках задач і методах буді-
вельної механіки, створення комп’ютерних технологій аналізу роботи конструкцій. Виникла можливість значно більшого наближення розрахункових схем до реальних об’єктів, урахування властивостей матеріалу споруд. Головним в оцінюванні методів стала їхня універсальність і надійність, можливість застосування до аналізу широкого класу систем, комп’ютерна технологічність. Будівельна механіка вийшла за межі стержневих систем і стала фунда-
ментальною наукою з розрахунку конструкцій. Сформувались нові її розділи – такі, як ймовірнісні методи розрахунку і теорія надійності, динамічна стійкість, нелінійна теорія оболонок, оптимальне проектування тощо.
Розвитку комп’ютерних методів аналізу сприяли праці Дж.Аргіріса, О.Зенкевича,
А.Ф.Смирнова, А.В.Александрова, Б.Я.Лащеннікова, М.М.Шапошникова, В.І.Феодосьєва,
А.С.Вольміра, Л.А.Розіна, А.П.Філіна, Р.А.Резнікова, Д.В.Вайнберга, П.М.Сосіса, Н.П.Абов-
ського, А.М.Масленікова, А.А.Чіраса та багатьох інших вчених.
У сучасній будівельній механіці широко застосовуються методи механіки деформівного твердого тіла. На основі розвитку варіаційних принципів і методів дискретизації значного розвитку набув метод скінченних елементів (МСЕ), на базі якого створені і вельми поширені у світовій практиці універсальні програмні комплекси з розрахунку широкого класу конструкцій.
У розвитку і використанні МСЕ суттєву роль відіграли праці Дж.Аргіріса, О.Зенкевича, Бате і Вілсона, Одена, Р.Клафа, Л.А.Розіна, А.П.Філіна, А.А.Александрова, М.М.Шапошнікова,
В.А.Постнова, І.Ф.Образцова, П.М. Варвака, О.С. Сахарова та ін.
Завдяки комп’ютеризації і застосуванню чисельних методів широкого розвитку набули динамічні задачі будівельної механіки, чому сприяли праці Р.Клафа, В.І.Феодосьєва,
А.С.Вольміра, Б.Г.Коренева, О.В.Лужина, А.П.Філіппова, В.А.Лазаряна, Г.С.Писаренка.
З кожним роком зростає роль експериментальних методів, які надають суттєву інформацію про поведінку під дією навантаження реальних конструкцій та їхніх моделей.
Значний внесок у розвиток будівельної механіки зробили вчені, які працювали в Україні − В.Л.Кирпичов, С.П.Тимошенко, Є.О. Патон, К.К.Сімінський, О.М.Дінник, М.М.Крилов,
М.М.Боголюбов, М.В.Корноухов, Б.М.Горбунов, Ф.П.Бєлянкін, О.А.Уманський, М.Д.Жудін,
Д.В.Вайнберг, М.О.Кільчевський, А.Д.Коваленко, В.Г.Чудновський, О.І.Стрельбицька,
1.Вступ |
17 |
|
|
І.Я.Штаєрман, О.І.Виноградов, П.М. Варвак, Я.Д.Лівшиць, І.Є.Прокопович, В.А.Лазарян,
М.Г.Бондар, А.П.Філіппов та ін.
В.Л.Кирпичову належать праці в галузі методів розрахунку статично невизначуваних стержневих систем. Він також відомий як організатор вищої освіти в Україні. У 1885−1898 рр. −
засновник і перший директор Харківського технологічного (надалі − політехнічного), в 1898−1902 рр. − засновник і перший директор Київського політехнічного інституту.
Всесвітнє визнання здобули праці видатного українського вченого-механіка С.П.Тимошенка
(1878−1972), зокрема, в розвитку теорії стійкості пружних систем, варіаційних методів,
прикладної теорії пружності тощо. Його фундаментальні підручники з опору матеріалів, статики споруд, теорії пружності витримали найбільшу кількість видань і перекладів і нині широко використовуються у навчальних закладах світу. Він також відомий працями з історії науки і техніки, організації вищої технічної освіти. С.П.Тимошенко в 1917−1920 рр. працював про-
фесором Київського політехнічного інституту, брав участь в організації Української Академії наук, 1919−1920 − перший директор Інституту технічної механіки Української Академії наук. У 1920 р. емігрував до Югославії, з 1922 р. жив і працював у США, з 1960 р. − у Німеччині.
У галузі будівництва мостів велику роль відіграли дослідження Є.О.Патона (1870−1953), які започаткували розвиток раціональних схем і рішень. М.В.Корноухов (1903−1958) відомий фун-
даментальними працями у галузі методів дослідження стійкості рамних конструкцій, які увійшли до наукової і навчальної літератури. Д.В.Вайнберг (1905−1973) досяг істотних результатів у галузі прикладної теорії пружності, теорії пластин і оболонок. Він був ініціатором широкого розвитку загальних чисельних методів і програмного забезпечення аналізу інженерних кон-
струкцій.
При організації Української Академії наук у 1918 р. створений інститут технічної механіки, у 1929 р. він перейменований в Інститут будівельної механіки, а у 1959 р. − в Інститут механіки АН УРСР, нині це Інститут механіки ім. С.П.Тимошенка Національної Академії наук України.
Значна роль у розвитку будівельної механіки належить Г.С.Писаренку, який упродовж багатьох років очолював кафедру опору матеріалів Київського політехнічного інституту, був засновником і першим директором Інституту проблем міцності НАН України.
У даний час дослідження у галузі будівельної механіки на Україні проводяться в наукових установах НАН України (Інституті механіки ім. С.П.Тимошенка, Інституті проблем міцності та ін.), в системі Міністерства освіти і науки України − науково-дослідному інституті будівельної механіки, на кафедрах вищих навчальних закладів, в галузевих науково-дослідних інститутах та інших установах.
1.Вступ |
18 |
|
|
Розвиток сучасної будівельної механіки, відбувався, з одного боку, шляхом створення і удосконалення чисельних методів і комп’ютерних технологій дослідження складних конструкцій, а з іншого − шляхом уточнення розрахункових схем, вихідних гіпотез, моделей реальної поведінки матеріалу, в тому числі з плином часу в процесі експлуатації, умов наван-
таження, можливих відхилень розрахункових величин навантаження від дійсних тощо.
Більшість задач сучасної техніки потребує оптимізаційних вирішень, вивчення фізичних явищ,
пов’язаних із характером навантажень. (Наприклад, розрахунки корпусів ядерних реакторів,
морських бурових платформ, ракет, космічних систем тощо). Підвищується роль експе-
риментальних методів. Будівельна механіка дедалі більше пов’язується з прикладною і обчислю-
вальною математикою, системним програмуванням, теорією оптимізації, фізикою,
проектуванням конструкцій, технологією їхнього виготовлення, проектним менеджментом,
економікою.

ДО ЗМІСТУ ПІДРУЧНИКА
I. ОСНОВНІ ПОНЯТТЯ, ПРИНЦИПИ І РІВНЯННЯ
БУДІВЕЛЬНОЇ МЕХАНІКИ СТЕРЖНЕВИХ
СИСТЕМ
2.Кінематичний аналіз і основи статичного розрахунку
3.Теорія переміщень
4.Загальні рівняння будівельної механіки
5.Енергетичні теореми і варіаційні принципи будівельної механіки
Методи будівельної механіки мають своїм підгрунтям деякі основні поняття. принципи та рівняння,. які використовуються під час розрахунків будь-яких конструкцій і споруд.
У першу чергу це принципи, які дозволяють створювати складні споруди з окремих елементів.
Ці питання розглядаються в главі Кінематичний аналіз і основи статичного розрахунку. Тут також визначаються способи обчислення реакцій вхаємодії між елементами та внутрішніх зусиль в їх перерізах.
Під впливом зовнішніх дій у спорудах виникають зусилля (внутрішні сили), які характеризують напружений стан, а також деформації елементів, які спричиняють появу переміщень точок споруди і визначають деформований стан системи. Питанням обчислення переміщень та їх основним властивостям присвячено главу Теорія переміщень.
Питання побудови повної системи рівнянь будівельної механіки (рівняня статики, геометричні
і фізичні рівняння) викладаються в главі Загальні рівняння будівельної механіки.
Напружено-деформований стан будь-якої системи може бути визначений як за допомогою аналізу повної системи рівнянь будівельної механіки, так і шляхом варіаційного числення.
Основними поняттями тут є енергія деформації системи, робота зовнішніх і внутрішніх сил і т.ін.
Означений підхід спирається на екстремальні принципи, виходячи з яких можна вивчати із за-
гальних позицій як задачі статики, так і задачі динаміки і стійкості, а відтак такі принципи можуть вважатися універсальними. Варіаційний підхід наведено в главі Енергетичні теореми і варіаційні
принципи будівельної механіки

ДО ЗМІСТУ ПІДРУЧНИКА
2. Кінематичний аналіз і основи статичного
розрахунку
З м і с т г л а в и
2.1. Основні поняття кінематичного аналізу
2.1.1. Геометрично незмінювані розрахункові схеми
2.1.2. Геометрично змінювані розрахункові схеми
2.1.3. Миттєво змінювані розрахункові схеми
2.2. Конструктивні елементи розрахункових схем
2.2.1. Диски
2.2.2. З’єднувальні пристрої
2.2.3. Зв’язок між простими з’єднувальними пристроями
2.2.4. Опорні пристрої
2.3. Кількісний етап кінематичного аналізу
2.4. Якісний (структурний) етап кінематичного аналізу
2.4.1. Приєднання шарнірного вузла до диска (спосіб “ діад”)
2.4.2. З’єднання двох дисків
2.4.3. З’єднання трьох дисків (спосіб шарнірного трикутника)
2.5. Послідовність виконання кінематичного аналізу
2.6. Приклади кінематичного аналізу розрахункових схем споруд
2.7. Статичний метод розрахунку
2.7.1. Визначення реакцій в’язей − зовнішня задача
2.7.2. Визначення зусиль в елементах споруди − внутрішня задача
2.8. Кінематичний метод
2.9. Матриця рівнянь рівноваги

2.Кінематичний аналіз |
2 |
2.10. Особливості роботи геометрично змінюваних систем
2.1. Основні поняття кінематичного аналізу
Кожна споруда впродовж її експлуатації повинна зберігати свою первісну форму та положення при дії на неї будь– яких зовнішніх навантажень. Незначні зміни розмірів споруди та її елементів можуть відбуватись лише за рахунок їх деформації.
Дослідження відповідності споруди цій вимозі виконується за допомогою кінематичного аналізу. До того ж у багатьох випадках кінематичний аналіз споруди дозволяє визначити найбільш раціональну послідовність її розрахунку. Зазначимо, що під “ спорудою” мається на увазі її розрахункова схема.
Усі сили, що діють на споруду, можна поділити на зовнішні та внутрішні. До зовнішніх належать як безпосередньо діючі на споруду навантаження, так і реакції опор, що прикріплюють її до землі. Всі сили, які виникають у тілі елементів і у в’язях, що з’єднують ці елементи, при розгляді всієї споруди вважаються внутрішніми силами.
Статичний розрахунок споруд полягає у визначенні сил, які виникають в її елементах під
впливом різних прикладених до цієї споруди зовнішніх дій − навантажень.
Між тим, під час розрахунку споруд, які складаються з кількох елементів (дисків), виявляється зручнішим, а іноді й конче необхідним, розглядати окремі їх елементи або групи елементів. У
такому випадку реакції в’язей, які з’єднують окремі елементи чи їх групи з відокремленою від них частиною споруди, також вважаються зовнішніми силами.
Проблему статичного розрахунку можна, таким чином, розділити на дві задачі:
1. Визначення реакцій в’язей, що виникають між елементами споруд, в тому числі й реакцій
опорних пристроїв − зовнішня задача.
2. Визначення внутрішніх сил, до яких належать інтегральні характеристики напружень, що
виникають в елементах споруди в процесі їхнього деформування, − внутрішня задача.
Зауважимо, що внутрішні сили в поперечному перерізі стержня можна розглядати також як реакції в’язей, якщо умовно вважати, що стержень складається з двох частин, розташованих по обидві сторони від цього перерізу, які з’єднуються за допомогою припайки.
У цій главі розглядається кінематичний аналіз і основи статичного розрахунку плоских стерж-
невих систем.

2.Кінематичний аналіз |
3 |
2.1.1. Геометрично незмінювані розрахункові схеми
Геометрично незмінюваними розрахунковими схемами є такі, що не змінюють свого положення та форми, якщо припустити, що їхні елементи виготовлені з абсолютно твердого матеріалу (такого, що не деформується).
Приклад найпростішої геометрично незмінюваної системи у вигляді шарнірного трикутника наведено на рис.2.1. Справді, якщо стержні AB, AC і BC не деформуються, зміна положення шарніра C стосовно шарнірів A і B можлива лише за рахунок повороту стержнів AC і BC довкола шарнірів A і B, що неможливо через відсутність спільної ділянки шляху відповідних дуг.
2.1.2. Геометрично змінювані розрахункові схеми
Геометрично змінюваними розрахунковими схемами називаються такі, що можуть істотно змінити свою форму, якщо навіть припустити, що їх елементи виготовлено з абсолютно твердого матеріалу.
Приклад найпростішої геометрично змінюваної системи у вигляді шарнірного чотирикутника показано на рис.2.2. Пунктиром показано нову форму, яку може одержати розрахункова схема без будь-яких змін у розмірах її елементів.
Рис.2.1 |
Рис.2.2 |
2.1.3. Миттєво змінювані розрахункові схеми
До миттєво змінюваних відносять такі розрахункові схеми, точки яких здатні переміщуватись без зміни геометричних розмірів їх елементів з точністю до малих вищого порядку.
Насправді, у миттєво змінюваній системі, зображеній на рис.2.3, дуги AC і BC, за якими можуть повернутись відповідні стержні довкола шарнірів A і B, мають спільну дотичну, і тому точка C
може переміститися по вертикалі на деяку відстань без істотної зміни довжин цих стержнів.
Рис.2.3
Як показано далі, розв’язання рівнянь для визначення зусиль в миттєво змінюваних системах призводить до одержання нескінченних або невизначених значень.

2.Кінематичний аналіз |
4 |
2.2. Конструктивні елементи розрахункових схем
Розрахункова схема споруди складається з конструктивних елементів, які можна поділити на два види: диски та з’єднувальні пристрої.
2.2.1. Диски
Диском може бути названо будь-який елемент чи частину розрахункової схеми, якщо заздалегідь задана або доведена її геометрична незмінюваність. Диском можна назвати й усю систему, якщо вона напевно геометрично незмінювана.
Особливо слід відзначити поняття простого диска, до якого відносять геометрично незмінювану плоску однозв’язну фігуру, тобто таку фігуру, всі границі якої можна “ обійти” вздовж однієї неперервної лінії, не перетинаючи тіло фігури.
На рис.2.4 зображено приклади простих плоских дисків, де пунктирними лініями показано неперервні лінії “ обходу” їхніх границь. Окремими випадками простих плоских дисків є прямолі-
нійний (рис.2.4,в), криволінійний (рис.2.4,г) і ламаний (рис.2.4,д) стержні, а також диск нескінченно малих розмірів, або матеріальна точка (рис.2.4,е).
Рис.2.4
На рис.2.4,ж зображено диск, який не можна вважати простим, оскільки він не є однозв’язним.
Насправді, і це випливає з рисунка, можна “ обійти” всі його границі (і зовнішні і внутрішні), лише перетнувши його тіло хоча б один раз.
Простий плоский диск скінченних розмірів має три, а матеріальна точка – два ступня вільності. Нагадаємо, що ступнем вільності диска або системи дисків називається кількість незалежних геометричних параметрів, що визначають положення диска (системи дисків) стосовно будь-якої системи координат.
Кількість ступнів вільності диска або системи дисків характеризується кількістю незалежних переміщень (лінійних чи кутових), які можуть здійснювати елементи системи або вся система

2.Кінематичний аналіз |
5 |
стосовно системи координат. Можливість цих переміщень може бути усунена за допомогою з’єднувальних пристроїв.
2.2.2. З’єднувальні пристрої
З’єднувальний пристрій (з’єднання) − це елемент розрахункової схеми споруди, який певним чином обмежує взаємне переміщення дисків, що з’єднуються цим пристроєм, зменшуючи її ступінь вільності.
Водночас кожен з’єднувальний пристрій має певні статичні властивості, що характеризуються кількістю та видом реактивних сил, що виникають у ньому.
У плоских розрахункових схемах застосовують такі основні типи з’єднань: кінематичну в’язь,
циліндричний шарнір, муфту, припайку.
Кінематична в’язь з’єднує два диски (елементи С1, С2 і С3 на рис.2.5,а,б,в) та перешкоджає поступальному переміщенню одного диска стосовно другого у напрямку осі, що проходить через точки шарнірного приєднання в’язі до дисків. Тобто в’язь усуває один ступінь вільності, проте допускає взаємний поворот 1 дисків та взаємне поступальне переміщення 2 по нормалі до осі цієї в’язі.
Рис.2.5
У кінематичній в’язі виникає реактивна сила (реакція) R, лінія дії якої проходять вздовж осі в’язі (рис.2.5,г,д.е).
Простий циліндричний шарнір ( Ш1 на рис.2.6,а) з’єднує два диски, усуваючи можливість їхніх взаємних поступальних переміщень. Але він допускає їх взаємний поворот стосовно осі,
яка проходить через центр шарніра. Отже, це з’єднання зменшує кількість незалежних параметрів руху дисків на два, тобто усуває два ступні вільності.

2.Кінематичний аналіз |
6 |
Рис.2.6
Реакція R (рис.2.6,б) у циліндричному шарнірі являє собою силу, яка проходить через його центр, але має заздалегідь невідомий напрямок, який може бути визначений у подальшому розрахунку. При аналітичному розрахунку її звичайно замінюють на дві складові V і H, які зручно обрати взаємно ортогональними (рис.2.6,в).
Муфта (Mi на рис.2.7,а) допускає лише одне взаємне переміщення − поступальне переміщення двох дисків уздовж фіксованої прямої. Це з’єднання зменшує кількість незалежних параметрів
руху дисків на два, тобто усуває два ступні вільності.
Реакція в муфті представляє силу R, нормальну до напрямку можливого взаємного поступального переміщення дисків і розміщену з ексцентриситетом e стосовно центра муфти O
(рис.2.7,б). Звичайно цю реакцію замінюють на дві складові − силу R1 і момент M, віднесши їх до центра муфти O (рис.2.7,в).
Рис.2.7 |
Рис.2.8 |
Проста припайка (Пi на рис.2.8,а) повністю виключає взаємні поступальні та кутові переміщення двох дисків, які нею з’єднуються. Це з’єднання зменшує кількість незалежних параметрів руху дисків на три, тобто усуває три ступні вільності.

2.Кінематичний аналіз |
7 |
Реакція в припайці − це сила R, лінія дії та ексцентриситет e якої стосовно центра припайки O
заздалегідь невідомі (рис.2.8,б). Цю реакцію зручно замінювати на три складові, віднесені до центра припайки O: двох взаємно перпендикулярних сил V і H, а також моменту M (рис.2.8,в).
2.2.3. Зв’язок між простими з’єднувальними пристроями
Між різними простими з’єднаннями існує взаємний зв’язок, який, якщо це необхідно або зручно для проведення аналізу, надає змогу замінювати одні з’єднання іншими, не змінюючи при цьому їх кінематичні та статичні властивості.
Так, простий циліндричний шарнір Ш1,2 (рис.2.9,а), що усуває два взаємних поступальних переміщення дисків Д1 і Д2, можна замінити на дві кінематичні в’язі С1 і С2 (рис.2.9,б), що пере-
тинаються в центрі шарніра, що замінюється.
Рис.2.9
Навпаки, будь-які дві кінематичні в’язі С1 і С2, які з’єднують пару дисків Д1 і Д2, можуть розглядатись як циліндричний шарнір Ш1,2, розташований в точці перетину цих в’язей
(рис.2.9,в,г). Такий уявний шарнір називають фіктивним.
Муфту М1,2 (рис.2.10,а) може бути замінено на дві паралельні кінематичні в’язі С1 і С2, осі яких перпендикулярні до можливого взаємного переміщення з’єднаних дисків Д1 і Д2 (рис.2.10,б).
Очевидно, це з’єднання може розглядатись також як фіктивний шарнір, розташований на перетині паралельних в’язей С1 і С2, тобто на нескінченному віддаленні.
Рис.2.10

2.Кінематичний аналіз |
8 |
Просту припайку П1,2 (рис.2.11,а) можна замінити на три кінематичні в’язі С1,С2 і С3, осі яких не паралельні та не перетинаються в одній точці (рис.2.11,б), або на шарнір Ш1,2 і кінематичну в’язь С1,2, що не проходить через центр шарніра Ш1,2 (рис.2.11,в).
Рис.2.11
У розрахункових схемах споруд, окрім розглянутих простих з’єднувальних пристроїв,
використовуються також складні, або кратні шарніри та складні, або кратні припайки.
Складним (кратним) вважається шарнір, що з’єднує більш ніж два диски. Такий шарнір може бути замінено на прості шарніри, кількість яких на одиницю менша від кількості з’єднуваних дисків. Наприклад, складний шарнір Шi на рис.2.12,а, що з’єднує чотири диски Д1, Д2, Д3 і Д4,
еквівалентний трьом простим шарнірам.
Рис.2.12
Аналогічно визначається складна (кратна) припайка. Так, на рис.2.12,б зображено складну припайку Пi, що еквівалентна чотирьом простим припайкам.
2.2.4. Опорні пристрої
Якщо з’єднувальний пристрій приєднує споруду чи якийсь її елемент до опорного диска
−“ землі”, кажуть, що такий пристрій є опорним, або опорою. В плоских розрахункових схемах застосовують такі типи опорних пристроїв (опор): шарнірно-рухому опору (рис. 2.13,а), яка еквівалентна простій кінематичній в’язі; шарнірно-нерухому опору (рис.2.13,б), що відповідає

2.Кінематичний аналіз |
9 |
простому циліндричному шарніру; повзун (рис.2.13,в), ідентичний до муфти, та жорстке затиснення (рис.2.13,г), яке є простою припайкою.
Рис.2.13
На наведених для кожної опори схемах показано різні способи їх зображення в розрахункових схемах, їхні кінематичні властивості, тобто можливі складові переміщень стосовно “ землі”, та їхні статичні властивості, тобто складові реакцій, які передаються на елементи споруди з боку “ землі”.
2.3. Кількісний етап кінематичного аналізу
Як уже зазначалось, з погляду кінематичного аналізу кожна споруда складається з дисків і матеріальних точок. Вони мають певну кількість ступнів вільності і з’єднувальних пристроїв, що обмежують можливості взаємних переміщень дисків, усуваючи відповідну кількість ступнів вільності.
Кількісний етап має за мету визначення кількості ступнів вільності всієї розрахункової схеми, тобто сумарної кількості ступнів вільності (кількість незалежних параметрів руху), які визначають положення елементів системи стосовно якоїсь нерухомої системи координат. Цю величину називають ступнем геометричної змінюваності системи.

2.Кінематичний аналіз |
10 |
Виходячи з викладених кінематичних властивостей елементів розрахункової схеми споруди,
можна записати формулу (модифікацію формули Чебишова) для визначення ступня геометричної
змінюваності Г системи: |
|
Г = 3 Д + 2В − 3П − 2Ш − С − 3, |
(2.1) |
де Д − кількість простих дисків, включаючи опорний диск “ землю”, якщо система прикріплена до неї; В − кількість вузлів в’язей, тобто кількість матеріальних точок (рис.2.14,а), тобто точок, в
яких з’єднуються тільки кінематичні в’язі (рис.2.14,б); П − кількість простих припайок; Ш −
кількість простих шарнірів; С − кількість простих в’язей (стержнів); 3 (три) − число ступнів вільності всієї плоскої розрахункової схеми як твердого тіла на площині.
Рис.2.14
Опорні пристрої приймаються в формулі відповідно до еквівалентних з’єднувальних пристроїв. Складні шарніри та припайки зараховуються як відповідна до них кількість простих шарнірів і припайок.
Ступінь геометричної змінюваності розрахункової схеми, обчислену за формулою (2.1), дає змогу визначити її кінематичну характеристику:
– Якщо Г > 0, розрахункова схема споруди безперечно є геометрично змінюваною. Цей результат засвідчує, що з’єднувальних пристроїв не вистачає для усунення можливості переміщень, які можуть робити окремі елементи системи або вся система в цілому.
Якщо Г ≤ 0, можна стверджувати, що виконується необхідна умова геометричної незмінюваності розрахункової схеми, бо з’єднувальні пристрої можуть забезпечити нерухомість усіх елементів і системи в цілому. Проте з’єднувальні пристрої можуть бути встановлені в такий спосіб, що в одних зонах конструкції кількість їх надмірна, а в інших − недостатня. Скажімо, дві розрахункові схеми, зображені на рисунках 2.15,а і 2.15,б, мають однакову кількість всіх елементів, і для обох систем обчислення за (2.1) досягається результат Г = 0.

2.Кінематичний аналіз |
11 |
Рис.2.15
Проте очевидно, що система на рис.2.15,а геометрично незмінювана, а система на рис.2.15,б
геометрично змінювана, оскільки правий її диск може повернутись довкола шарніра B. У деяких випадках розташування з’єднувальних пристроїв може приводити до появи миттєвого центра взаємного обертання елементів системи.
Таким чином, при Г ≤ 0 розрахункова схема може бути або геометрично незмінюваною, або геометрично змінюваною, або, нарешті, миттєво змінюваною залежно від розташування дисків і з’єднань. Належність до конкретного типу остаточно встановлюється на підставі виконання якісн-
ого етапу аналізу розрахункової схеми.
2.4. Якісний (структурний) етап кінематичного аналізу
Якісний (структурний) етап аналізу розрахункової схеми полягає у визначенні послідовності та способів утворення системи з елементів. З’єднання всієї системи або її фрагментів повинно виконуватись відповідно до способів правильного з’єднання елементів у геометрично незмінювані системи.
Далі наведені основні способи утворення найпростіших геометрично незмінюваних плоских систем при використанні мінімальної кількості з’єднувальних пристроїв. Для зручності подальшого викладу надамо цим способам певні назви.
При поданні цих способів і прикладів структурного аналізу зручно використовувати умовну
“ формулу”, яка буде розміщуватись поруч з відповідною схемою з’єднання. Така “ формула” виглядає як дріб, де в чисельнику міститься перелік з’єднаних елементів, а у знаменнику − перелік з’єднувальних пристроїв, а після символа − позначення нового укрупненого диска. Якщо з’єднання виконано за допомогою фіктивного шарніра, в знаменнику подається найменування двох в’язей, що утворюють цей шарнір, із символом “ ד між ними.
2.4.1. Приєднання шарнірного вузла до диска (спосіб “ діад”)
Шарнірний вузол (матеріальну точку) B можна приєднати до диска Д за допомогою двох кіне-
матичних в’язей С1 і С2, що не лежать на одній прямій (рис. 2.16,а). Якщо в’язі С1 і С2 розташовані на одній прямій (рис.2.16,б), утворюється, так звана, миттєво змінювана система, яку не можна
використовувати в будівництві.

2.Кінематичний аналіз |
12 |
Рис.2.16 Рис.2.17
З’єднання трьох кінематичних в’язей трьома шарнірами (див.рис.2.1) можна розглядати як спосіб “ діад”, якщо одну кінематичну в’язь, наприклад AB, розглядати як диск, до якого двома в’язями приєднується вузол C.
2.4.2. З’єднання двох дисків
Зручно розглядати три способи приєднання одного диска до іншого, хоча використання відповідності між різними з’єднувальними пристроями дає змогу привести їх один до одного.
За способом припайки два диски Д1 і Д2 можуть бути з’єднані між собою за допомогою припайки П (рис.2.17).
Спосіб Полонсо полягає в тому, що два диски Д1 і Д2 можна з’єднати шарніром Ш і
кінематичною в’яззю С, що не проходить через центр шарніра Ш (рис.2.18,а). Якщо в’язь С проходить через центр шарніра Ш (рис.2.18,б), одержана таким чином система є миттєво змінюва-
ною.
Рис.2.18
Як спосіб Полонсо можна трактувати попарне з’єднання трьох кінематичних в’язей трьома шарнірами (див.рис.2.1): два диски AC i BC з’єднуються кінематичною в’яззю AB та шарніром C.
Спосіб Шухова передбачає, що два диски Д1 і Д2 можуть бути з’єднані трьома кінематичними в’язями С1, С2 і С3, які не перетинаються в одній точці, а отже, й не паралельні між собою
(рис.2.19,а). Якщо три з’єднувальні в’язі С1, С2 і С3 одночасно перетинаються в одній точці О
(рис.2.19,б) або всі вони паралельні одна щодо одної (рис.2.19,в), то утворена система буде миттєво змінюваною.

2.Кінематичний аналіз |
13 |
Рис.2.19
В останньому випадку якщо в’язі С1, С2 і С3 матимуть однакову довжину, система двох дисків
буде геометрично змінюваною (рис.2.19,г).
2.4.3. З’єднання трьох дисків (спосіб шарнірного трикутника)
Три диски Д1, Д2 і Д3 можна з’єднати за допомогою трьох шарнірів (реальних або фіктивних)
Ш1,2, Ш1,3 і Ш2,3, які не лежать на одній прямій (рис.2.20,а). Причому фіктивні шарніри (але не більш, ніж два з них) можуть бути і нескінченно віддаленими.
Рис.2.20
Так, усі три шарніри Ш1,2, Ш1,3 і Ш2,3, які з’єднують три диски Д1, Д2 і Д3 на рис.2.20,а, є
дійсними. На рис.2.20,б диски Д1 і Д3 з’єднані дійсним шарніром Ш1,3, диски Д1 і Д2 − фіктивним
2.Кінематичний аналіз |
14 |
шарніром Ш1,2, розташованим у точці перетину в’язей С1 і С2, що його утворили, а диски Д2 і Д3 −
фіктивним шарніром Ш2,3, утвореним в’язями С3 і С4 і розташованим на їх перетині. На рис.2.20,в
всі три з’єднувальних шарніри є фіктивними: диски Д1 і Д2 з’єднані в’язями С1 і С2, що утворю-
ють шарнір Ш1,2, розташований на їх перетині, в’язі С3 і С4 з’єднують диски Д1 і Д3 і утворюють на своєму перетині шарнір Ш1,3, шарнір Ш2,3, що з’єднує диски Д2 і Д3 через в’язі С5 і С6, нескінченно віддалений.
Якщо три шарніри Ш1,2, Ш1,3 і Ш2,3, дійсні чи фіктивні, розташовані на одній прямій
(рис. 2.20,г) або всі нескінченно віддалені, то кажуть, що система з трьох дисків Д1, Д2 і Д3 є
миттєво змінюваною.
2.5. Послідовність виконання кінематичного аналізу
Виконання кінематичного аналізу розрахункової схеми споруди можна поділити на три етапи.
∙Кількісний аналіз. На цьому етапі за допомогою формули Чебишова (2.1) обчислюють ступінь геометричної змінюваності розрахункової схеми споруди. Якщо одержано результат Г > 0,
можна відразу, не виконуючи другого етапу аналізу, дійти висновку щодо геометричної змінюваності розрахункової схеми внаслідок недостатньої кількості з’єднувальних пристроїв.
Якщо Г ≤ 0, можна зробити попередній висновок, що необхідна умова геометричної незмінюваності системи задовільняється, тобто, інакше кажучи, система може бути гео-
метрично незмінюваною. В цьому випадку треба перейти до виконання наступного етапу аналізу.
∙Якісний (структурний) аналіз полягає в дослідженні послідовності з’єднання елементів відповідно до викладених вище способів утворення найпростіших геометрично незмінюваних систем. Якщо встановлено, що якісь два чи три елементи з’єднані правильно за одним із цих способів, такий фрагмент системи можна розглядати як новий укрупнений диск та використовувати сукупно з іншими елементами для утворення нових геометрично незмінюваних фрагментів. Цей процес потрібно продовжувати доти, поки не буде проана-
лізоване приєднання всіх елементів розрахункової схеми споруди.
∙Остаточний висновок про геометричну незмінюваність, геометричну або миттєву змінюваність розрахункової схеми споруди. Якщо доведено правильне приєднання всіх елементів системи, вся розрахункова схема може вважатись геометрично незмінюваною. Якщо виявляється, що для з’єднання одних елементів використані зайві пристрої, а для інших їх бракує, всю розрахункову схему вважають геометрично змінюваною. Якщо ж хоча б одне

2.Кінематичний аналіз |
15 |
з’єднання виконується за винятком з якогось способу, що відповідає миттєвій змінюваності фрагмента, розрахункова схема вважається миттєво змінюваною.
Таким чином, для геометричної незмінюваності плоскої розрахункової схеми споруди необхідне задоволення двох умов: необхідна умова − Г ≤ 0; достатня умова − правильність утворення системи.
2.6. Приклади кінематичного аналізу розрахункових схем споруд
2.6.1. Кінематичний аналіз розрахункової схеми (рис. 2.21,а).
Рис.2.21
Перш, ніж розпочати кінематичний аналіз прикріпленої до “ землі” розрахункової схеми споруди, доцільно:
∙окремі ділянки “ землі” об’єднати в єдиний опорний диск таким чином, щоб інша частина схеми залишалась за його межами (на рис.2.21,а це поєднання для шарнірно-нерухомої опори B і
шарнірно-рухомої опори A подано пунктирною лінією);
2.Кінематичний аналіз |
16 |
· опорні пристрої показати у вигляді, зручному для проведення кінематичного аналізу.
Кількісний аналіз. При виконанні аналізу можливі різні варіанти трактування структури розрахункової схеми споруди. Для прикладу розглянемо два варіанти.
У першому варіанті (рис.2.21,б) розглянемо схему як сукупність трьох простих дисків Д1, Д2,
Д3, одного простого опорного шарніра Ш1 і чотирьох кінематичних в’язей С1, С2, С3 і С4.
Тоді параметри, що входять до формули Чебишова (2.1), набирають таких значень: Д = 3, В =
0, П = 0, Ш = 1, С = 4; отже
Г= 3×3 + 2×0 - 3×0 - 2×1 - 4 - 3 = 0.
Удругому варіанті (рис.2.21,в) будемо вважати, що та ж сама схема складається з дисків Д1, Д2,
Д3, Д4, Д5, Д6, простих шарнірів Ш2, Ш3, Ш4, Ш5, Ш6, Ш7 і опорних кінематичних в’язей С4, С5 і
С6. Тобто Д = 6 , П = 0, В = 0, Ш = 6, С = 3 і ,таким чином,
Г = 3×6 + 2×0 –3 ×0 – 2 ×6 – 3 – 3 = 0.
Отже, розрахункова схема може бути геометрично незмінюваною.
Як бачимо, результат кількісного аналізу не залежить від трактування опису структури розрахункової схеми.
Якісний аналіз. Визначаємо таку послідовність складання (монтажу) розрахункової схеми,
щоб на кожному його етапі утворювалась геометрично незмінювана частина схеми за допомогою будь-якого з відомих п’яти способів з’єднання елементів.
Так, для даного прикладу можна визначити два етапи монтажу. На першому етапі (рис.2.21,г)
диски Д1 і Д2 з’єднуються трьома кінематичними в’язями С1, С2 і С3, які не перетинаються в одній точці та не паралельні між собою (спосіб Шухова). Цю частину розрахункової схеми можна розглядати як укрупнений диск D1. Укрупнені диски позначатимемо латинською літерою D з ін-
дексом, що відповідає порядковому номеру його створення.
На другому етапі монтажу приєднання нового укрупненого диска D1 до диска-” земля” Д3
можна трактувати двома способами, виходячи з відповідного варіанта опису розрахункової схеми
(див. рис.2.21,б,в) - за способом Полонсо, тобто за допомогою шарніра Ш1 і кінематичної в’язі С4,
що не проходить через шарнір Ш1 (рис.2.21,д), або за способом Шухова, тобто за допомогою трьох кінематичних в’язей С4, С5 і С6, що не перетинаються в одній точці та не паралельні між собою.
На другому етапі утворюється новий укрупнений диск D2, що являє собою всю розрахункову схему, яка досліджується.
Висновок. Розрахункова схема споруди геометрично незмінювана.

2.Кінематичний аналіз |
17 |
2.6.2. Кінематичний аналіз розрахункової схеми (рис. 2.22,а)
Рис.2.22
Кількісний аналіз. Усі шарніри цієї схеми можна вважати вузлами кінематичних в’язей. Тому її структуру можна розглядати як сукупність вузлів В і кінематичних в’язей С (рис.2.22,б),
причому кількість таких вузлів В = 6, а кількість в’язей С = 9.
Тоді Г = 3×0 + 2×6 - 3×0 - 9 - 3 = 0.
Отже, розрахункова схема може бути геометрично незмінюваною.
Якісний аналіз. Створення цієї розрахункової схеми споруди можна представити у вигляді трьох етапів монтажу.
На першому етапі (рис.2.22,в) укрупнений диск D1 утворюється з’єднанням трьох дисків Д1, Д2,
Д3 трьома шарнірами Ш1, Ш2 і Ш3, які не лежать на одній прямій (спосіб шарнірного трикутника).
На другому етапі можна довести попереднім способом створення нового укрупненого диска D2.
Але для різноманітності уявімо цей диск (рис.2.22,г) як з’єднання диска Д4 і вузла В4 двома кіне-
матичними в’язями С4 і С5, що не лежать на одній прямій (спосіб діад).
На третьому етапі (рис.2.22,д) укрупнені диски D1 і D2 з’єднуються за допомогою трьох кінематичних в’язей С7, С8 і С9. Однак ці в’язі перетинаються в одній точці.
Висновок. Розрахункова схема споруди, що розглядається, миттєво змінювана.

2.Кінематичний аналіз |
18 |
2.6.3. Кінематичний аналіз розрахункової схеми (рис. 2.23,а)
Рис.2.23
Кількісний аналіз. Значення величин, що використовуються в формулі Чебишова (2.1),
визначаємо за схемою, поданою на рис.2.23,б, яку одержано з вихідної позначенням опорного диска-” землі” Д1, заміною складних шарнірів A,B,C і E парами простих шарнірів, уявленням шарнірно-нерухомої опори A простим шарніром Ш1, а шарнірно-рухомої опори B - кінематичною в’яззю С1.
Тоді одержуємо Д = 4, В = 0, П = 0, Ш = 1, С = 7 і зрештою
Г = 3×4 + 2×0 − 3×0 − 2×1 − 7 − 3 = 0.
Отже, розрахункова схема може бути геометрично незмінюваною.
Якісний аналіз. Створення системи здійснюється в два етапи.
На першому етапі укрупнений диск D1 складається з трьох дисків Д2, Д3, Д4, з’єднаних трьома фіктивними шарнірами Ш2,3, Ш3,4 і Ш2,4 (рис.2.23,в), які не лежать на одній прямій, причому шарнір Ш3,4 розташований у нескінченності. Кожний фіктивний шарнір одержано на перетині двох кінематичних в’язей, що з’єднують відповідну пару дисків.
Другий етап (рис.2.23,г) полягає в приєднанні укрупненого диска D1 до опорного диска Д1
способом Полонсо за допомогою шарніра Ш1 і в’язі С1, яка не проходить через шарнір Ш1. Таким чином, уся розрахункова схема являє собою диск D2.
Висновок. Розрахункова схема споруди, що розглядається, геометрично незмінювана.

2.Кінематичний аналіз |
19 |
2.6.4. Кінематичний аналіз розрахункової схеми, зображеної на рис.2.24,а
Кількісний аналіз. Для зручності дослідження перемалюємо розрахункову схему (рис.2.24,б).
Рис.2.24
З цією метою покажемо диск-” земля” Д1, прості диски Д2-Д6, прості шарніри Ш1, Ш2, Ш3 і
припайку П1, замінимо шарнірно-рухомі опори C і F кінематичними в’язями С1 і С2, а також замість складного шарніра E покажемо два еквівалентних щодо нього простих шарніри Ш4 і Ш5.
Використовуючи одержану схему, визначимо геометричну змінюваність за формулою Чебишова
(2.1):
Г = 3×6 + 2×0 - 3×1 - 2×5 - 2 - 3 = 0.
Отже, розрахункова схема може бути геометрично незмінюваною.
Якісний аналіз. Розглянемо послідовність монтажу системи.
На першому етапі (рис.2.24,в) диск Д2 приєднаний до диска Д1 припайкою П1 , створюючи
укрупнений диск D1.
Другий етап (рис.2.24,г) полягає в з’єднанні трьох дисків Д3, Д4, і Д5 за допомогою трьох шарнірів Ш2, Ш3 і Ш4, що не лежать на одній прямій. При цьому утворюється укрупнений диск D2.
Далі (рис.2.24,д) два укрупнених диски D1 і D2 з’єднуються способом Полонсо за допомогою шарніра Ш1 і в’язі С1, яка не проходить через Ш1, утворюючи новий укрупнений диск D3.
2.Кінематичний аналіз |
20 |
Нарешті на четвертому етапі (рис.2.24,е) до D3 приєднується диск Д6 способом Полонсо за допомогою шарніра Ш5 і в’язі С2, що не проходить через Ш5. Таким чином утворюється новий диск D4, який являє собою всю досліджувану систему.
Висновок. Розрахункова схема споруди, що розглядається, геометрично незмінювана.
2.7. Статичний метод розрахунку
Найбільш поширеним і загальним способом розв’язання як зовнішньої, так і внутрішньої задачі статики є використання методу перерізів. Цей метод полягає в тому, що від споруди наскрізним перерізом, який проходить через з’єднання, відокремлюється якийсь її фрагмент (елемент, група елементів). Розрізані в’язі (з’єднання) відкидаються і замінюються силами − реакціями цих в’язей.
Таким чином, на відокремлений фрагмент діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень і реакцій відкинутих в’язей.
Фрагмент споруди під дією системи зовнішніх сил відповідно до аксіоми статики може розглядатися як абсолютно тверде тіло. Тому до цієї системи сил можна застосувати умови її рівноваги, які дають змогу визначити невідомі реакції в’язей.
2.7.1. Визначення реакцій в’язей − зовнішня задача
Кількість реакцій в’язей, що з’єднують між собою елементи споруди і всю споруду до землі
R = С + 2Ш + 3П, |
(2.2) |
де С − кількість простих в’язей, Ш − кількість простих шарнірів, |
П − кількість простих |
припайок. |
|
Кількість рівнянь рівноваги, що можна скласти для розрахункової схеми споруди, яка
складається з Д простих дисків і В вузлів в’язей, визначається виразом |
|
U = 3 Д + 2В − 3. |
(2.3) |
При цьому беруть до уваги те, що до диска прикладається довільна система сил, для якої можна скласти три рівняння рівноваги; на вузол в’язів діє збіжна система сил, для якої можна записати два рівняння рівноваги; доданок "– 3" введено у цей вираз тому, що рівняння рівноваги складаються стосовно нерухомої системи координат, що зв’язана з одним із дисків, який вважається нерухомим (наприклад, із землею).
Якщо кількість невідомих реакцій в’язей R збігається з кількістю рівнянь рівноваги U, які можна вивести для всіх елементів системи, то всі реакції в’язей можуть бути визначені з одержаної системи рівнянь.

2.Кінематичний аналіз |
21 |
Розрахункові схеми споруд, для яких всі реакції в’язей можуть бути визначені з рівнянь рівноваги (рівняння статики), належать до статично визначуваних систем.
Якщо кількість невідомих реакцій в’язей R перевищує кількість рівнянь рівноваги U, для визначення реакцій самих цих рівнянь недостатньо і необхідно вдаватися до використання додаткових умов. Означені системи називаються статично невизначуваними.
Число, відповідне перевищенню кількості реакцій в’язей над кількістю рівнянь рівноваги,
називається ступнем статичної невизначуваності системи:
n = R − U = (С + 2Ш + 3П) − (3 Д + 2В − 3) = − Г. |
(2.4) |
Отже, для геометрично незмінюваних і статично визначуваних систем виконується будь-яке з двох співвідношень:
n = 0 |
або |
Г= 0. |
(2.5) |
Для геометрично незмінюваних і статично невизначуваних систем
n > 0 |
або |
Г < 0. |
(2.6) |
Для визначення реакцій в’язей геометрично незмінюваних і статично визначуваних систем, що задовольняють співвідношенню (2.5), застосовується метод перерізів.
При цьому замкненими перерізами можна відокремити всі диски та вузли в’язей, що складають систему. Для кожного диска, на який діє довільна система сил, і кожного вузла, що перебуває під дією збіжної системи сил, можна скласти рівняння рівноваги. Реакції в’язей можуть бути визначені з одержаної системи лінійних рівнянь.
Зазначимо, що рівність нулю визначника матриці коефіцієнтів цієї системи рівнянь засвідчує,
що розрахункова схема споруди миттєво змінювана.
Між тим застосування системи сумісних рівнянь для визначення реакцій в’язей недоцільно через значну трудомісткість. Необхідно намагатись складати рівняння рівноваги в такий спосіб,
щоб кожна невідома реакція визначалася з одного незалежного рівняння, в крайньому випадку для їх визначення необхідно було б розв’язати систему двох рівнянь із двома невідомими.
Цієї мети можна досягти, якщо визначення реакцій в’язей пов’язувати зі способом з’єднання елементів у геометрично незмінювану систему, оскільки кожному способу з’єднання відповідає доцільний спосіб складання рівнянь рівноваги. Розглянемо ці способи.
Спосіб діад. Для визначення реакцій двох в’язей, що приєднують шарнірний вузол до диска
(рис.2.25,а), вузол відокремлюється від диска замкненим перерізом 1-1 (рис.2.25,б).

2.Кінематичний аналіз |
22 |
Рис.2.25
Для визначення реакцій вязей R1 і R2 складаються два рівняння рівноваги одержаної таким чи-
ном системи збіжних сил. Кожне рівняння вміщуватиме тільки одне невідоме, якщо координатні осі спрямовувати перпендикулярно до кожної з двох в’язей:
∑Fy = 0 |
R1 ; |
∑Fz = 0 |
R2 . |
Якщо два диски з’єднуються припайкою (рис.2.26,а), доцільно провести замкнений переріз 1-1
через центр О припайки.
Рис.2.26
У місці розрізу прикладаються невідомі реактивні сили. Для однієї з відокремлених частин,
наприклад, правої частини (рис.2.26,б), можна скласти три рівняння рівноваги, кожне з яких містить одну невідому величину:
∑M O = 0 |
M o ; |
∑ Fx = 0 |
Ho ; |
∑ Fy = 0 |
Vo . |
У системах, що створені способом Полонсо (рис.2.27,а), необхідно визначити реакції в шарнірі
C і кінематичній в’язі AB, що з’єднують два диски.

2.Кінематичний аналіз |
23 |
Рис.2.27
Для цього виконується замкнений переріз 1-1 через шарнір C і в’язь AB (рис.2.27,а). Цей переріз поділяє систему на дві частини. Реакція R у в’язі AB спрямована вздовж її осі. Невідома реактивна сила в шарнірі C відображається двома складовими, одну з яких Hc зручно спрямувати паралельно, а другу Vc − перпендикулярно до реакції R. Реакції R, Vc і Hc визначаються з рівнянь рівноваги будь-якої з відокремлених частин, наприклад, правої:
∑M C = 0 |
R; |
∑Fy = 0 |
Vc ; |
∑M E = 0 |
H c . |
Для визначення реакцій трьох в’язей, що з’єднують два диски системи, утвореної за способом Шухова (рис.2.28,а), виконується наскрізний замкнений переріз 1-1 і розглядається рівновага будь-якого з дисків.
Рис.2.28
На рис.2.28,б показаний правий диск. На нього діє зовнішня сила P2 і невідомі реакції в’язей
R1, R2 і R3. Можна скласти три рівняння рівноваги цього диска, що відповідає кількості невідомих.
Для того щоб кожне рівняння містило лише одну невідому реакцію в якійсь кінематичній
в’язі, запишемо рівняння у вигляді суми моментів сил стосовно точки перетину двох інших
в’язей. Цей спосіб складання рівнянь називається способом моментної точки (спосіб
Ріттера), а відповідні точки називаються моментними точками або точками Ріттера.
Наприклад:

2.Кінематичний аналіз |
24 |
∑M A = 0; P2 × l + R3 |
× r3 = 0; R3 = -P2 |
l |
. |
|
|||
|
|
r |
|
|
|
3 |
|
Реакції R1 і R2 визначаються відповідно з аналогічних рівнянь рівноваги |
|||
∑M B = 0 R2 ; |
∑M C = 0 R1. |
|
|
Якщо дві з трьох кінематичних в’язей системи, створеної за способом Шухова (рис.2.29,а), не паралельні одна одній (наприклад, в’язі С1 та С2) то реакцію третьої в’язі визначають таким самим чином, як і в попередньому випадку.
Рис.2.29
Моментна точка для кінематичної в’язі С2 розташована на нескінченності. Тому для виз-
начення реакції R2 не може бути використано рівняння моментів, і рівняння рівноваги складається в формі суми проекцій сил, що діють на відокремлену частину, на вісь, що перпендикулярна до двох інших паралельних в’язей. Розглядаючи, наприклад, праву частину (рис.2.29,б), рівняння рівноваги можна записати у вигляді
∑Fy = 0; R2cosα - P3cosβ = 0; R2 |
= P3 |
cos β |
. |
|
|||
|
|
cos α |
|
Розглянемо визначення реакцій у трьох шарнірах, що з’єднують три диски за способом шарнірного трикутника (рис. 2.30,а).
Рис.2.30

2.Кінематичний аналіз |
25 |
Наскрізним замкненим перерізом, що перетинає два будь-яких шарніри (наприклад перерізом
1-1 через шарніри A і B), розділяємо систему на дві частини і розглядаємо рівновагу частини, яка складається з двох дисків Д1 і Д2 (рис. 2.30,б). Реакцію в кожному розрізаному шарнірі зображуємо у вигляді двох взаємно перпендикулярних складових VA і HA (в шарнірі A) і VB та HB (в шарнірі B).
При цьому складові HA і HB спрямовуємо по прямій, що з’єднує центри розрізаних шарнірів A і B.
Складові VA і VB можуть бути визначені з рівнянь рівноваги:
∑M A = 0 VB ; ∑ M B = 0 VA .
Виконаємо наскрізний переріз 2-2 через третій шарнір C відокремленої частини і розглянемо рівновагу одного з дисків, наприклад Д2 (рис. 2.30,в). Складові VC і HC реакції в шарнірі C
спрямуємо паралельно до відповідних складових реакцій у шарнірах A і B.
Складові VA і VB вже відомі, тому з умов рівноваги диска одержуємо
∑M C = 0 H A ; ∑M E = 0 HC ;
∑ Fy = 0 VC .
Нарешті, складову HB можна обчислити з рівняння рівноваги системи дисків Д1-Д2:
∑ Fx = 0 H B .
Якщо три диски з’єднані способом шарнірного трикутника шістьма кінематичними в’язями,
що утворюють три фіктивних шарніри (рис.2.31,а), реакції в цих в’язях визначаються таким чином.
Рис.2.31

2.Кінематичний аналіз |
26 |
У кожному фіктивному шарнірі розташована точка прикладання рівнодіючої реакцій у в’язях,
що складають цей шарнір. Означену рівнодіючу можна відобразити будь-якими двома складовими, наприклад R1 і R3, R2 і R4 (рис.2.31,б), R5 і R6 (рис.2.31,в,г). Їхні напрямки визнача-
ються лише зручністю розрахунку.
Розглядаючи рівновагу частини системи на рис.2.31,б, можна визначити R1 і R2 з рівнянь:
∑M B = 0 R1 ; ∑M A = 0 R2 .
Переходячи до рівноваги диска Д1 (рис.2.31,в), можна визначити R3, R5 і R6 з рівнянь:
∑M C = 0 R3 ; ∑M E = 0 R6 ;
∑ Fz = 0 R5 .
Нарешті, розглядаючи рівновагу диска Д2 (рис.2.31,г), одержимо R4:
∑M C = 0 R4 .
Визначивши складові R1...R6, обчислимо реакції в кінематичних в’язях, розкладаючи R1...R6 по напрямках відповідних в’язей.
Розглянемо визначення реакцій кінематичних в’язей у двох окремих випадках розташування в’язей при з’єднанні трьох дисків за допомогою способу шарнірного трикутника. Ці окремі випадки зображено на рис. 2.32,а і 2.33,а.
Рис.2.32

2.Кінематичний аналіз |
27 |
Система на рис.2.32,а відрізняється від розглянутої раніше тим, що дві кінематичні в’язі С1 і С2
паралельні і відповідний фіктивний шарнір розташований на нескінченності. Тому перерізи
(рис.2.32,а,б,в), послідовність визначення реакцій у в’язях R1, R2 і R6 та рівняння рівноваги, що використовуються для цього, аналогічні викладеним у попередньому випадку. Відмінність у рівняннях рівноваги, що застосовуються для визначення реакцій R3, R5 і R4:
на підставі рис.2.32,в
∑ Fy = 0 R3 ; ∑M D = 0 R6 ;
на підставі рис. 2.32,г:
∑Fy = 0 R4 .
Усистемі, що показана на рис.2.33,а, чотири кінематичні в’язі попарно паралельні: С1 і С2, С5 і
С6. Послідовність визначення реакцій у в’язях така.
Рис.2.33
Для зрівноваженої частини системи, що відокремлена замкненим наскрізним перерізом 1-1 (рис.2.33,б), можна скласти рівняння рівноваги, з якого визначається реакція R4:
∑Fx = 0 R4 ,
попередньо зобразивши рівнодіючу реакції у в’язях С3 і С4 двома складовими, з яких одну,
наприклад R3, спрямувавши паралельно до реакцій R1 і R2.
Далі наскрізним замкненим перерізом 2-2 поділяємо схему на рис.2.33,б на дві частини, кожна з яких зображена на рис.2.33,в,г.

2.Кінематичний аналіз |
28 |
Розглядаючи рівновагу частини на рис.2.33,в, одержуємо
∑ Fy = 0 R3 ; ∑M A = 0 R5 ;
∑M C = 0 R6 .
Зумов рівноваги частини на рис.2.33,г маємо
∑ M E = 0 R1 ; ∑ M iD = 0 R2 .
Визначення реакцій в’язей складеної розрахункової системи базується на якісному етапі кінематичного аналізу. До складених належать такі розрахункові схеми, які побудовані як завершення кількох послідовних етапів приєднання елементів до раніше створених дисків.
Упослідовності, протилежній приєднанню чергових елементів до дисків, тобто розпочинаючи
зостаннього приєднання, необхідно відокремлювати ці елементи, проводячи замкнені наскрізні перерізи через в’язі, що їх прикріплюють.
Розглядаючи умови рівноваги кожної відокремленої частини системи, можна визначити реакції перерізаних в’язей. Ці реакції необхідно прикладати як зовнішні сили до фрагментів, до яких прикріплено досліджену частину, у протилежному напрямі і враховувати їх у подальших розрахун-
ках разом із навантаженням.
Якщо вважати, що створення геометрично незмінюваної системи відбувається як послідовний монтаж з окремих елементів, то визначення реакцій в’язей систем можна уявити як її демонтаж. Цілком природно, що послідовність демонтажу повинна бути протилежною послі-
довності монтажу.
Приклад 2.1. Визначити реакції в’язей розрахункової схеми споруди, яка зображена на
рис.2.34,а, якщо d=2 м, P1=20 кН, P2=40 кН.
Рис.2.34

2.Кінематичний аналіз |
29 |
Кінематичний аналіз цієї розрахункової системи викладено в п.п. 2.6.3. Результат кількісного етапу Г = 0, свідчить, що система статично визначувана, тобто всі реакції в’язей можуть бути
визначені за допомогою рівнянь рівноваги, складених для всієї системи та її окремих частин.
Під час кінематичного аналізу встановлено, що останнім було приєднання всієї системи як диска до землі. Тому насамперед замкненим перерізом відокремлюємо диск D1 від землі,
перетинаючи при цьому опорний шарнір A, зображений у вигляді шарнірно-нерухомої опори, і
опорну кінематичну в’язь B - шарнірно-рухому опору.
На диск D1 (рис.2.34,б), окрім заданих зовнішніх сил P1 і P2, з боку відкинутого диска-“ землі”
діють реакції шарнірно-нерухомої опори A і шарнірно-рухомої - B. Лінія дії реакції RB
перпендикулярна до можливого напряму руху опори B: Лінія дії реакції шарнірно-нерухомої опори A невідома, тому зображуємо цю реакцію у вигляді двох складових - вертикальної VA і
горизонтальної HA.
Складаючи три рівняння рівноваги довільної системи сил, що діють на диск, визначаємо три
невідомі реакції: |
|
|
∑ Fx = 0; |
HA + P2 = 0; |
HA = – 40 кН; |
∑ MA = 0; – P 2 d – P 1 ×2d + RB ×4d = 0; |
RB = 20 кН; |
|
∑ Fy = 0; |
VA + P1 – V B =0; |
VA = 0. |
Зображуємо робочу схему (рис.2.35,а), |
на якій на відміну від рис. 2.34,б реакції VA, HA і RB |
|
показано як відомі сили з урахуванням зміни напряму HA внаслідок набутого від’ємного значення.
Рис.2.35
2.Кінематичний аналіз |
30 |
За цією робочою схемою виконуємо перевірку обчислень, використовуючи інше рівняння
рівноваги |
|
|
|
|
∑ MB = 0; |
– 40×3d + 40×2d – 20×2d + 20×4d = 0. |
|
||
Рівняння задовольняється, що свідчить про правильність визначення VA, HA і RB. |
||||
Розглянемо диск D1 |
(див.рис.2.23,г), утворений способом шарнірного трикутника. |
|||
Відокремлюємо від нього замкненим перерізом I фрагмент |
(рис.2.35,а) і використовуємо рівняння |
|||
рівноваги фрагмента (рис.2.35,б), з яких обчислюємо реакції в’язей R4 і R5: |
||||
∑ Fy = 0; |
20 + R5×cos45° =0; |
R5 = – 28,29 кН; |
||
∑ MK = 0; |
– 20 ×d – R 4 × d = 0; |
R4 = – 20 кН. |
|
|
Реакцію R3 обчислюємо з рівняння рівноваги фрагмента (рис. 2.35,в), відокремленого від диска |
||||
D1 замкненим перерізом II (рис.2.35,а): |
|
|
||
∑MF = 0; |
– 40×d/3 – |
40×2d/3 – R 4×4d/3 – R 3×7d/3 = 0; |
R3 = – 5,72 кН. |
|
Повернемось до фрагмента на рис.2.35,б: |
|
|
||
∑ Fx = 0; |
– R 3 + R2 – R 4 + R5×cos45° = 0; |
R2 = – 5,72 кН. |
||
Знову розглянемо рівновагу фрагмента на рис.2.35,в: |
|
|||
∑ M0 = 0; |
40×d – 40×2d +5,72×d + R1×r1 = 0; |
R1 = 13,56 кН; |
||
∑Fx = 0; |
40 – 40 |
+ R1×cosa+ R4 + R3 + R6×cosa = 0; R6 = 13,56 кН. |
||
Числові значення кута a і плеча r1, які входять у ці рівняння, визначаємо заздалегідь, виходячи з геометричних розмірів розрахункової схеми.
Визначені значення реакцій можна перевірити, складаючи додаткове рівняння рівноваги для фрагмента системи на рис.2.35,г, яка відокремлена від диска D1 перерізом III :
∑ Fy = 0; – R 1×sina + R6×sina – R 5×cos45° – 20 = 0;
– 13,56×sina + 13,56×sina + 28,29×cos45° – 20 = 24,29 – 24,29 = 0 .
Приклад 2.2. Визначити реакції в’язей розрахункової схеми споруди, що зображена на рис.2.36,а.

2.Кінематичний аналіз |
31 |
Рис.2.36
Кінематичний аналіз цієї розрахункової системи викладено в п.2.6.4. Результат кількісного етапу Г = 0, свідчить, що система статично визначувана, тобто всі реакції в’язей можуть бути визначені за допомогою рівнянь рівноваги. Такі рівняння потрібно складати як для всієї системи,
так і для її окремих частин. Нагадаємо, що ці частини повинні відокремлюватись у послідовності,
зворотній щодо їх приєднання при створенні системи, яка встановлена при виконанні якісного етапу кінематичного аналізу.
У першу чергу визначимо реакції в шарнірі E і шарнірно рухомій опорі F, які останніми приєднували простий диск Д6 до системи. Для цього відокремлюємо диск замкненим перерізом по шарніру E і опорі F та зображуємо його окремо (рис.2.36,б). Для системи довільних сил, що діють на нього, складаємо три рівняння рівноваги, з яких визначаємо дві складові VE і HE реакції в шарнірі E і реакцію опори RF:
∑ ME = 0; |
6×5 + RF×4 = 0; |
RF = – 7,5 кН; |
∑ Fx = 0; |
– 7,5 + HE = 0; |
HE = 7,5 кН; |
∑ Fy = 0; |
– 6 + VE = 0; |
VE = 6 кН. |
2.Кінематичний аналіз |
32 |
Величини визначених реакцій для зручності подальшої роботи позначаємо на рисунку. При цьому змінюємо на протилежний напрям реакції RF, яка в результаті обчислення виявилась від’ємною.
Для перевірки обчислень складаємо додаткове рівняння рівноваги
∑ MF = –7,5 ×4 + 6×5 = 0.
Далі відокремлюємо перерізом складений диск, який було приєднано передостаннім
(рис.2.36,в). При цьому перерізаються шарнір B і шарнірно рухома опора C. На складений диск діють зосереджені сила P1 і момент M1, визначені складові реакції VE і HE приєднаного диска з протилежним напрямом та невідомі складові VB і HB реакції шарніра B і реакція RC в’язі C. Для визначення останніх скористуємось з трьох рівнянь рівноваги довільної системи сил:
∑ MB = 0; |
– 20 + 12 ×5 + 6×10 – 7,5 ×2 – RC ×8 = 0; |
RC = 10,625 кН; |
∑ MC = 0; |
– 20 – 12 ×3 + 6×2 – 7,5 ×2 + VB×8 = 0; |
VB = 7,375 кН; |
∑ Fx = 0; |
HB – 7,5 = 0 ; |
HB = 7,5 кН. |
Записуємо обчислені величини реакцій на рис.2.36,в і виконуємо їх перевірку за допомогою додаткового рівняння рівноваги
∑ Fy = 0; – 12 – 6 + 7,375 + 10,625 = 0 .
Розглянемо диск, який було приєднано до диска–“ земля” першим за допомогою припайки
(рис.2.36,г). До цього диска прикладені сили взаємодії між ним і диском, який спирається на нього, у вигляді реакцій VB і HB зі зворотним напрямом, та три невідомі складові VA, HA і MA
реакції затиснення A. Визначаємо ці складові, використовуючи рівняння рівноваги:
∑ Fx = 0; |
HA – 7,5 = 0 ; |
HA = 7,5 кН; |
∑ Fy = 0; |
VA – 7,375 = 0; |
VB = 7,375 кН; |
∑ MA = 0; |
– MA +7,375×6 = 0; |
MA = 44,25 кН. |
Далі необхідно визначити реакції в’язей, за допомогою яких утворений складений диск на рис.2.36,в. Для цього наскрізним перерізом через шарніри D і E відокремлюємо два диски
(рис.2.37,а). На ці два з’єднаних диски Д4 і Д5 діють зосереджені сила P1 і момент M1, а також чотири складові VD, HD, VE1 і HE1 реакцій шарнірів D і E. Реакції VE і HE диска Д6 можуть бути прикладені як до диска Д5, так і до диска Д3. Будемо вважати їх віднесеними до диска Д3, що уможливить вилучення їх з розгляду на даному етапі обчислень.

2.Кінематичний аналіз |
33 |
Рис.2.37
Для зображеної на рис.2.37,а довільної системи сил можна скласти три рівняння рівноваги, а
невідомих сил діє чотири. Одначе є можливість скласти два рівняння для визначення двох невідомих:
∑ MD = 0; |
– 20 + 12 ×5 – VE1×10 = 0; |
VE1= 4кН; |
∑ ME1 = 0; |
VB×10 – 20 – 12 ×5 = 0; |
VB = 8 кН. |
Відокремлюємо наскрізним перерізом через шарнір G диск Д5 (рис.2.37,б). До цього диска прикладені дві складові VG і HG реакції в шарнірі G і дві складові VE1 і HE1 реакції в шарнірі E1,
одну з яких (VE1) вже визначено. Три невідомі реакції визначаємо за допомогою трьох рівнянь рів-
новаги довільної системи сил: |
|
|
∑ MG = 0; |
4×5 + HE1×4 = 0; |
HE1 = 5 кН; |
∑ Fx = 0; |
HG – 5 = 0 ; |
HG = 5 кН; |
∑ Fy = 0; |
– V G + 4 = 0; |
VG = 4 кН. |
Складаючи раніше не використане третє рівняння рівноваги системи дисків на рис.2.37,а,
визначаємо невідому складову HD реакції шарніра D: |
|
|
∑ Fx = 0; |
HD – 5 = 0 ; |
HD = 5 кН. |
Для перевірки правильності визначення реакцій у внутрішніх з’єднаннях складеного диска розглянемо окремо зображений диск Д4 (рис. 2.37,в), до якого прикладені зосереджені сила P1 і M1
та обчислені раніше складові реакцій у шарнірах D і E1. Перевіряємо, чи задовольняються рівняння рівноваги:
2.Кінематичний аналіз |
34 |
∑ Fx = 0; |
5 – 5 = 0 ; |
∑ Fy = 0; |
8 – 12 + 4 = 0 ; |
∑ MD = 0; |
– 20 + 12 ×5 – 4 ×5 – 5 ×4 = 0. |
Рівняння задовольняються. Отже, реакції в шарнірах обчислені правильно.
Виконуємо перевірку визначення реакцій опор. З цією метою відокремлюємо всю розрахункову схему від диска–“ земля” ( рис.2.36,г). Прикладаємо всі навантаження і обчислені реакції опор. Складаємо рівняння рівноваги:
∑ Fx = 0; |
7,5 – 7,5 = 0 |
; |
∑ Fy = 0; |
7,375 – 12 + |
10,625 – 6 = 0 ; |
∑ MA = 0; |
– 44,25 – 20 + 12 ×11 – 10,625 ×14 + 6×21 – 7,5 ×6 = 0. |
|
Рівняння задовольняються. Отже реакції опор обчислені правильно.
2.7.2. Визначення зусиль в елементах споруди − внутрішня задача
Як уже зазначалося, при зовнішніх діях на споруди останні деформуються і в них виникають зовнішні та внутрішні сили. Якщо зовнішні сили, до яких належать безпосередньо прикладені до споруди силові фактори, в тому числі реакції в’язей, звичайно діють на неї дискретно, то внутрішні сили поширюються на все тіло елементів споруди.
У стержневих елементах покладено внутрішні сили відносити до кожного їх поперечного перерізу і прикладати до центра ваги перерізу. Внутрішні сили в перерізі стержня поділяють на згинальні моменти, поперечні та поздовжні сили.
Згинальним моментом у перерізі стержня називається головний момент усіх зовнішніх сил,
розташованих з одного боку від перерізу. Згинальний момент є інтегральною характеристикою нормальних напружень.
Згинальний момент у перерізі стержня визначається як сума моментів усіх сил, розташованих по один бік від перерізу, стосовно центра ваги перерізу.
Загальне правило знаків для згинальних моментів у стержневих системах не визначено. На епюрах згинальних моментів ординати необхідно відкладати з боку розтягнених волокон перерізу.
Для балок і арок згинальний момент вважається додатним, якщо він розтягує нижнє волокно перерізу.
Поперечною силою в перерізі стержня, яка є інтегральною характеристикою зсуваючих напру-
жень, називають проекцію головного вектора сил, розташованих з одного боку стержня, на площину перерізу.

2.Кінематичний аналіз |
35 |
Поперечна сила в перерізі стержня визначається як сума проекцій всіх сил, розташованих по один бік від перерізу, на нормаль до осі стержня в цьому перерізі.
Поперечна сила вважається додатною, якщо вона намагається повернути відповідну частину стержня за годинниковою стрілкою стосовно перерізу.
Поздовжньою силою в перерізі стержня, яка є інтегральною характеристикою напружень поздовжньої деформації, називають проекцію головного вектора сил, розташованих з одного боку стержня, на нормаль до площини перерізу.
Поздовжня сила в перерізі стержня визначається як сума проекцій всіх сил, розташованих по один бік від перерізу, на дотичну до осі стержня в цьому перерізі.
Поздовжня сила вважається додатною, якщо вона розтягує переріз.
Так, внутрішні сили в перерізі I-I стержня, зображеного на рис.2.38,а, можна визначити,
розглядаючи ліву від цього перерізу частину стержня. Тоді:
M |
I −I |
= |
∑ |
M |
лів. = -P ×r - P ×r + P ×r ; |
|
|
|
|
I −I |
1 1 2 2 3 3 |
||
QI −I |
= ∑ Fn |
лів. = −P1sinj − P2 cosj + P3sin( j + a3 ); |
||||
N I −I |
= ∑ Ft |
лів |
= −P1cosj + P2sinj + P3cos( j + a3 ). |
|||
Ті самі внутрішні сили можна визначити, розглядаючи праву від перерізу частину стержня:
M I − I = ∑ M Iп−р.I = P4 × r4 - P5 × r5 - M1;
QI −I = ∑ Fnпр = −P4 cos( j + a4 ) + P5 cosj;
NI − I = ∑ Ftпр = P4sin( j + a4 ) - P5sinj.
Рис.2.38

2.Кінематичний аналіз |
36 |
Слід зауважити, що при обчисленні величин Q і N знаки проекцій |
сил на осі n і t |
проставляються відповідно до правила знаків поперечних і поздовжніх сил, а не до напряму
координатних осей.
Визначення внутрішніх сил в перерізі стержня може бути зведено до розв’язання зовнішньої задачі, якщо розглядати стержень як два окремих стержні, з’єднаних в перерізі припайкою. У
цьому випадку згинальний момент у перерізі може тлумачитись як реактивний момент у припайці, а поперечна і поздовжня сили − як складові реакції припайки, відповідно паралельна і перпендикулярна до осі стержня в перерізі. Для визначення складових реакції припайки стержень перерізається по припайці та складаються рівняння рівноваги лівої (рис. 2.38,б) або правої (рис.2.38,в) частини стержня.
2.8. Кінематичний метод
Кінематичний метод ґрунтується на принципі можливих переміщень, згідно з яким для будь-
якої зрівноваженої системи сума робіт всіх сил на будь-яких можливих нескінченно малих перемі-
щеннях дорівнює нулю:
A = 0 . |
(2.7) |
Відповідно до цього принципу для визначення реакції якоїсь в’язі необхідно відкинути цю в’язь і натомість прикласти реакцію в’язі як зовнішню силу невідомої величини. Далі потрібно надати системі нескінченно мале переміщення в напрямі відкинутої в’язі, побудувати відхилений стан і прирівняти нулю суму робіт всіх зовнішніх сил на утворених переміщеннях. Шукана реакція визначиться із розв’язку цього рівняння.
Наприклад, обчислимо опорну реакцію VB балки (рис.2.39,а).
Рис.2.39

2.Кінематичний аналіз |
37 |
Відкинувши опору B (рис.2.39,б), одержимо механізм. Прикладемо реакцію опори VB як зовнішню силу. Надамо переміщення в точці B у напрямку цієї сили. Сума робіт всіх сил становитиме
A = −Py p + VB y = 0 ,
звідки VB = PyP y . |
|
|
|
|
|
|
З подібності трикутників |
|
|
|
|
|
|
|
y p |
= |
l + c |
|||
|
|
|
|
. |
||
|
y |
|
|
|||
|
|
|
l |
|||
Остаточно маємо |
|
|
|
|
|
|
V |
= |
l + c |
P . |
|||
|
||||||
|
B |
|
|
l |
||
|
|
|
|
|||
2.9. Матриця рівнянь рівноваги
Усі елементи будівельних конструкцій повинні перебувати у стані рівноваги. Виходячи з умов рівноваги обчислюються опорні реакції і внутрішні зусилля в окремих елементах. Але і системи,
складені з елементів, також повинні перебувати у стані рівноваги. Розглянемо складання рівнянь рівноваги для плоскої стержневої системи.
У будь-якій стержневій системі можна виділити два типи елементів: стержні і вузли. Під вузлами розумітимемо точки, де з’єднуються кілька стержнів. Сукупність рівнянь рівноваги,
складених для кожного стержня і для кожного вузла, може розглядатися як система рівнянь рівноваги всієї стержневої системи. Оскільки в кожному стержні за невідомі величини можна прийняти 6 кінцевих зусиль (M, Q, N – на одному і M, Q, N – на протилежному кінці стержня), а
також опорні реакції у вузлах, то для системи, яка містить S стержнів і R опорних реакцій,
загальна кількість невідомих становитиме k=6S+R. З іншого боку, для кожного стержня і для кожного вузла можна скласти по три рівняння рівноваги. Отже, якщо система з S стержнями має u
вузлів, то загальна кількість рівнянь становитиме m=3S+3u.
Рівняння рівноваги для вузлів доцільно записувати, використовуючи загальну систему координат усієї стержневої системи. При складанні рівнянь рівноваги для стержнів виявляється зручним обирати для кожного стержня свою власну систему координат x’y’ . Початок такої системи координат розташовують на кінці стержня, який прилягає до вузла із меншим номером.
Цю точку вважають початком, а протилежну − кінцем стержня. Вісь x’ спрямовують вздовж стержня від його початку до кінця, а вісь y’ − перпендикулярно до стержня. Таку систему

2.Кінематичний аналіз |
38 |
координат називають місцевою або локальною.
Розглянемо стержневу систему (рис.2.40,а), яка складається з трьох стержнів і чотирьох вузлів.
Розкладання системи на стержні і вузли показано на рис.2.40,б.
Рис.2.40
Внутрішні зусилля в перерізах стержня 1-2 (рис.2.40.,в) спрямовані відповідно до правилу знаків для простих балок: додатні поздовжні сили викликають розтягування стержня, поперечні сили намагаються повернути стержень за годинниковою стрілкою, згинальні моменти викликають розтягнення в “ нижньому” волокні стержня (розташування “ верхнього” або “ нижнього” волокна визначається напрямом осі y’ місцевої системи координат стержня).
З умов рівноваги стержня 1-2 маємо:
∑Fx′
∑Fy′
∑M1
=0 − N1−2 + N2−1 = 0;
=0 Q1−2 − Q2−1 − ql1−2 = 0;
=0 Q2−1l1−2 + M1−2 − M 2−1 + ql12−2 / 2 = 0.
Для вузла 1 (рис.2.40,г)
2.Кінематичний аналіз |
39 |
∑Fx = 0
∑Fy = 0
∑M1 = 0
Для стержня 2-3 (рис.2.40,г)
∑Fx′ = 0
∑Fy′ = 0
∑M 2 = 0
Для вузла 2 (рис.2.40,е)
∑Fx = 0
∑Fy = 0
∑M 2 = 0
Для стержня 3-4
∑Fx′ = 0
∑Fy′ = 0
∑M 3 = 0
H1 + N1−2cosα + Q1−2sinα = 0;
V1 + N1−2sinα − Q1−2cosα = 0;
−M1−2 = 0.
−N2−3 + N3−2 = 0; Q2−3 − Q3−2 = 0;
Q3−2l2−3 + M 2−3 − M 3−2 = 0.
N2 −3 − N2 −1cosα − Q2 −1sinα + Pcosβ = 0;
−Q2 −3 − N2 −1sinα + Q2 −1cosα − Psinβ = 0;
−M 2 −3 + M 2 −1 = 0.
−N3−4 + N4−3 = 0;
Q3−4 − Q4−3 = 0;
Q4−3l3−4 + M 3−4 − M 4−3 = 0.
Аналогічні рівняння можна скласти для вузла 3:
∑ Fx = 0 ∑ Fy = 0 ∑M 3 = 0
і для вузла 4:
∑Fx = 0 ∑Fy = 0 ∑M 4 = 0
−N3−2 + Q3−4 + H3 = 0;
−Q3−2 − N3−4 = 0;
M 3−2 − M 3−4 − M = 0
Q4 −3 + H 4 = 0;
N4 −3 + V4 = 0;
M 4 −3 + M 4 = 0.
Одержані рівняння можна записати у вигляді табл.2.1, де кожен рядок відповідає одному рівнянню, а кожен стовпець − невідомому зусиллю або опорній реакції.

2.Кінематичний аналіз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 2.1 |
||||
|
N1-2 |
Q1-2 |
|
M1-2 |
|
N2-1 |
|
Q2-1 |
|
M2-1 |
|
V1 |
|
H1 |
|
N2-3 |
|
… |
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
|
0 |
|
1 |
|
0 |
|
|
0 |
|
|
0 |
|
0 |
|
0 |
|
|
… |
|
0 |
|
|
|
|
0 |
1 |
|
0 |
|
0 |
|
-1 |
|
|
0 |
|
|
0 |
|
0 |
|
0 |
|
|
… |
|
ql1-2 |
|
|
|
|
0 |
0 |
|
1 |
|
0 |
|
l1-2 |
|
|
-1 |
|
0 |
|
0 |
|
0 |
|
|
… |
|
−ql |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−2 |
|
|
|
|
cosα |
sinα |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
1 |
|
0 |
|
|
… |
|
0 |
|
|
|
|
sinα |
-cosα |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
1 |
|
0 |
|
0 |
|
|
… |
|
0 |
|
|
|
|
0 |
0 |
|
1 |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
0 |
|
0 |
|
|
… |
|
0 |
|
|
|
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
0 |
|
-1 |
|
… |
|
0 |
|
|
|
|
|
… |
… |
… |
… |
|
… |
|
… |
|
… |
|
… |
|
… |
|
… |
|
|
|
|
|
|
… |
|
|
|
|
У матричній формі рівняння рівноваги матимуть вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.8) |
||
|
|
|
|
|
|
|
|
|
|
A S = F , |
|
|
|
|
|
|
|
|
|
|
|
|||||
де A− матриця коефіцієнтів рівнянь рівноваги: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
− 1 |
0 |
0 |
1 |
0 |
0 0 |
0 |
|
0 |
… |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
1 |
0 |
0 |
− 1 0 0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
0 |
0 |
1 |
0 |
l1−2 |
− 1 0 |
0 |
|
0 |
… |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = cosα |
|
sinα |
0 |
0 |
0 |
0 |
− 1 0 |
0 |
… . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
− cosα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinα |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
… |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 0 l2−3 |
0 |
… |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… … … … … … … … |
|
|
|
|
|
|
|||||||||||||
Сукупність внутрішніх зусиль на кінцях стержнів, а також опорних реакцій стержневої системи
представлені вектором
|
M |
|
N |
Q |
M |
V H N |
|
…} . |
ST = { N Q |
1−2 |
2−3 |
||||||
1−2 1−2 |
|
|
2−1 2−1 |
|
2−1 1 1 |
|
Вплив зовнішніх навантажень характеризується вектором
FT = {0 ql -ql2 2 0 0 0 0 }.
1−2 1−2 …
Залежно від кількості стержнів, вузлів і опорних в’язей можливі три випадки:
∙n = m, тобто кількість рівнянь відповідає кількості невідомих.. У цьому випадку матриця коефіцієнтів рівнянь рівноваги A є квадратною (рис.2.41,а).

2.Кінематичний аналіз |
41 |
Рис.2.41
a |
a |
… |
a |
|
11 |
12 |
|
1k |
|
A = a21 |
a22 |
… a2k . |
||
… |
… |
… |
… |
|
|
ak 2 |
|
|
|
ak1 |
… akk |
|||
Вектор зусиль визначається як розв’язок матричного рівняння
S = A −1F .
Наявність розв’язку означає, що система, яка розглядається, є геометрично незмінюваною і статично визначуваною.
Натомість, якщо матриця A є особливою, тобто якщо її визначник дорівнює нулю, то обернена матриця A-1 не існує, і, отже, рівняння не має розв’язку. Означений випадок відповідає миттєвій змінюваності системи.
∙n > m. Матриця A є прямокутною: кількість стовпців перевищує кількість рядків (рис.2.41,б),
тобто кількість невідомих перевищує кількість рівнянь. Це означає, що вихідна система є гео-
метрично незмінюваною і статично невизначуваною.
∙ n < m. Матриця A є прямокутною: кількість стовпців менше ніж кількість рядків (рис.2.41,в),
тобто кількість рівнянь перевищує кількість невідомих. Вихідна система є геометрично змінюваною.
Отже, вигляд матриці коефіцієнтів рівнянь рівноваги може розглядатись як статичний кри-
терій геометричної незмінюваності споруди.
Різновидом статичного критерію геометричної незмінюваності є спосіб нульового навантаження, який полягає в розрахунку системи при відсутності зовнішніх навантажень.

2.Кінематичний аналіз |
42 |
Розглянемо, наприклад, геометрично незмінювану систему двох дисків, що пов’язані трьома стержнями (рис.2.42,а), що не паралельні і не перетинаються в одній точці, тобто за способом Шухова за відсутністю зовнішніх сил.
Рис.2.42
Реакції у стержнях обчислюють з трьох умов рівноваги:
∑M k1 = 0 S1 = 0; ∑M k3 = 0 S3 = 0; ∑ Fy = 0 S2 = 0.
Отже, в геометрично незмінюваній системі в разі відсутності зовнішнього навантаження всі реакції дорівнюють нулю.
У миттєво змінюваній системі (рис.2.42,б), що утворена з двох дисків, які поєднуються трьома
паралельними стержнями, умова рівноваги ∑ Fy = 0 виконується тотожно при будь-яких
величинах реакцій розсічених в’язей, в тому числі і відмінних від нуля. Таким чином, неможливо довести дорівнювання нулю всіх реакцій в’язей.
Із розглянутих прикладів можна зробити висновок: якщо на базі рівнянь рівноваги можна довести, що за відсутності зовнішніх навантажень реакції всіх в’язей дорівнюють нулю, система геометрично незмінювана. Якщо це довести неможливо і відмінні від нуля реакції задовольняють умовам рівноваги, система миттєво змінювана.
2.10. Особливості роботи геометрично змінюваних систем
Як вже зазначалося, геометрично змінювані системи не зберігають своєї первісної форми при дії зовнішніх навантажень. Але це не означає, що зміна форми такої системи виключає можливість ії використання. Характерним прикладом такої системи є гнучка нитка. Ступінь геометричної змі-
нюваності гнучкої нитки нескінченно велика, оскільки положення її точок на площині

2.Кінематичний аналіз |
43 |
визначається нескінченною кількістю параметрів. Вона набуває тієї або іншої форми залежно від вигляду зовнішнього навантаження (рис.2.43).
Рис.2.43
Проаналізуємо докладніше роботу таких систем. В процесі аналізу геометрично змінювані системи можуть розглядатися як такі, що мають мінімально необхідну кількість в’язей, але реакції в одній або в кількох в’язях дорівнюють нулю за будь-яких навантажень.
Розглянемо стержень AB, який прикріплено до основи за допомогою шарніра A і завантажено зовнішньою силою P (рис.2.44,а).
Дана система є геометрично змінюваною, оскільки диск AB поєднуються з диском –“ земля” лише за допомогою шарніра. Отже в системі не вистачає одній кінематичної в’язі. Умовно накладемо цю в’язь, аби система перетворилася на геометрично незмінювану (рис.2.44,б) − на кінці B додамо опорний стержень.
Рис.2.44
Опорна реакція у стержні може бути обчислена з рівняння рівноваги елемента AB, який відсічений від опор (рис.2.44,в):
∑M A = 0 P × a - R ×b = 0

2.Кінематичний аналіз |
44 |
Тобто момент зовнішньої сили P зрівноважується моментом реактивної сили в додатковому опорному стержні.
Для еквівалентності заданої (рис.2.44,а) і перетвореної (рис.2.44,б) схем поставимо вимогу рівності нулю реакції в додатковому опорному стержні. Виходячи з цього момент зовнішньої сили буде неврівноваженим. Під дією цього моменту елемент AB буде обертатись стосовно точки A,
причому момент сили P змінюватиметься внаслідок зміни плеча a. Нарешті стержень дійде положення, коли плече a дорівнюватиме нулю (рис.2.44,г). В цьому положенні при навантаженні,
що розглядається, рівняння моментів задовольняється тотожно. Отже система перебуватиме в стані рівноваги і може бути розрахована звичайними методами.
Наступний приклад. Розглянемо систему, зображену на рис.2.45,а.
Рис.2.45
Система утворена з’єднанням диска CD із диском –“ земля” за допомогою лише двох кінематичних в’язей AC i BD. Вона є геометрично змінюваною: не вистачає однієї кінематичної в’язі. Для перетворення її у геометрично незмінювану накладемо на систему додаткову в’язь − стержень AD (рис. 2.45,б). Отже, можна розглядати знов утворену систему як таку, що утворена способом Шухова: диск CD з’єднується з диском–“ земля” за допомогою трьох кінематичних в’язей: AC, AD i BD. Для визначення реакцій в цих в’язях необхідно відокремити диск CD від
“ землі”, за допомогою перерізу, що розтинає ці в’язі (рис.2.45,в), і скласти три рівняння рівноваги.
Так, для обчислення реакції R AD необхідно скласти рівняння моментів стосовно точки K:
∑M K = 0 P × a + RAD × r = 0 .
2.Кінематичний аналіз |
45 |
Якщо поставити вимогу рівності нулю реакції R AD , то елемент CD знаходитиметься під дією |
|
незрівноваженого моменту |
P × a . В результаті елемент CD, а також в’язі AC і BD будуть |
переміщуватися, причому плече сили P буде змінюватися. В той момент, коли стержні CD і BD |
|
розташовуватимуться на одній прямій (рис.2.45,г), моментна точка реакції RAD буде збігатися з точкою C. Отже, плече зовнішньої сили P стане нульовим, зовнішній момент зникне, і рівняння моментів буде виконуватись тотожно. Таким чином, при зазначеному навантаженні геометрично змінювана система може умовно розглядатись як геометрично незмінювана.
На підставі наведених міркувань можна дійти такого висновку: геометрично змінювані
системи можуть змінювати свою форму, пристосовуючись до зовнішнього навантаження, і в
такому стані розраховуватись як геометрично незмінювані.
