
- •Зміст підручника
- •1. Вступ
- •3. Теорія переміщень
- •8. Ферми
- •9. Тришарнірні арки
- •10. Плоскі рами
- •11. Метод сил
- •12. Метод переміщень
- •13. Змішаний метод
- •V.ОСНОВИ ДИНАМІКИ І СТІЙКОСТІ СПОРУД
- •17. Коливання систем із нескінченно великим числом ступнів вільності
- •18. Метод скінченних елементів у задачах динаміки
- •19.Стійкість споруд
- •23. Статично визначувані ферми
- •24. Розпірні системи
- •26. Нерозрізні балки
- •VIII. НАВЧАЛЬНІ ПРОГРАМНІ КОМПЛЕКСИ
- •27. Навчальний програмний комплекс АСИСТЕНТ
- •28. Комп’ютерне самотестування рівня знань

О П А
|
|
|
|
|
|
|
|
|
3. Теорія переміщень |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Зміст глави |
|
|
|
|
|
|
||||||||||||
|
. |
. |
о ота |
|
овнішні і внутрішні |
сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
. |
. |
а ал нені сили і у а ал нені пере |
і енн |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
. |
. |
ніверсал ні по наченн |
пере і |
|
|
ен |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
. |
. |
атриц |
податливості і |
атриц |
жорсткості |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
. |
. |
нте рал |
ора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
. |
. Окре |
і випадки астосуванн |
фор |
ули |
аксвелла– |
ора |
|
|||||||||||||||||||||
|
. |
. О численн |
|
інте рала |
|
ора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
. |
. Пере |
і |
енн |
від ді те |
|
ператури |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
. |
. Пере |
і |
енн |
від при |
усово о |
|
і |
енн |
опор |
|
|
|
|
|
|
|
||||||||||||
|
. |
. Повна фор |
ула дл о численн |
|
пере і |
ен |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
. |
. |
еоре |
и в ає ності |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
. |
. . |
еоре |
а про в ає |
ніст |
ро |
іт |
теоре а Бетті |
|
|
|
|
||||||||||||||||
|
|
. |
. . |
еоре |
а про в ає |
ніст |
пере |
і |
|
ен |
теоре а |
аксвелла |
|||||||||||||||||
|
|
. |
. . |
еоре |
а про в ає |
ніст |
реакцій |
|
теоре |
а |
еле |
|
|
|
|||||||||||||||
|
|
. |
. . |
еоре |
а про в ає |
ніст |
реакцій і пере |
і |
ен |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Під впливо |
овнішні |
дій і навантажен |
споруди дефор уют с . |
При ц о у координати, о |
||||
арактери уют |
положенн |
кожно о |
перері у, |
інюют с , то то |
перері и пере і уют с . |
|||
Ви наченн ци |
пере |
і |
ен |
авданн |
теорі |
пере |
і ен . |
|
О численн |
пере |
і |
ен |
нео ідно |
|
|
|
|
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
– дл |
ро ра унку споруд на жорсткіст , коли ви начают с |
най іл ші пере і |
енн |
перері ів |
||||||||||||
споруди fmax і порівнюют с пере і енн |
и, |
кі припускают с , то то перевір єт с у |
ова |
|||||||||||||
fmax |
[ f ]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– дл |
ро ра унку статично неви начувани |
систе |
при складанні рівн н |
су |
існості дефор |
ацій |
||||||||||
еле |
ентів споруди. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.1. обота зовнішніх і внутрішніх сил |
|
|
|
|
|
|
|
|
||||||||
к |
о до споруди прикладено певну силу, |
ка в процесі навантаженн |
ростає від нул |
до |
||||||||||||
кінцево |
величини |
|
порівн но |
невеликою |
швидкістю |
таке навантаженн |
на иваєт с |
|||||||||
статичним , |
споруда дефор |
уєт с , |
точки, |
в |
ки |
прикладено навантаженн , пере і |
уют с і |
|||||||||
сили дійснюют ро оту. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
о |
л не |
о статичне |
авантаженн стержн |
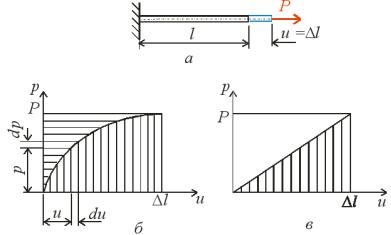
рис. . ,а , кий внаслідок ді |
ро т |
уючо сили P |
||||||||||
дістає |
подовженн |
l. |
к о |
атеріал стержн |
є |
фі ично-нелінійни , |
рафік |
алежності |
іж |
|||||||
навантаженн |
і пере |
і |
енн |
кінц |
стержн |
уде криволінійни рис. . |
, . |
|
|
|
|
|||||
ис. .
л о численн ро оти, ку виконала сила P, ві е о пере і енн u в довіл ний о ент часу і нада о йо у приріст du. оді ро ота сили виражаєт с інте рало
|
l |
|
|
Ap |
pdu |
|
(3.1) |
|
0 |
|
|
і вл є со ою пло у іж кривою і віссю u, |
ка на |
рафіку рис. . , |
аштри ована вертикал ною |
штри овкою. аку ро оту на ивают дійсною. |
|
|
|
к о ж надати приріст не пере і |
енню, |
а навантаженню, |
то ро ота виражати ет с |
інте рало |
|
|
|
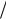
|
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Au |
udp . |
|
|
|
|
|
|
|
|
|
|
|
|
(3.2) |
||||
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аку ро оту на ивают |
додатковою. |
а |
рафіку |
рис. |
. , |
пло |
а, |
о відповідає додатковій |
||||||||||||||||||
ро оті, по начена ори онтал ною штри овкою. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
у |
а дійсно і додатково ро оти на иваєт с |
|
повною роботою |
овнішні |
сил |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
Aп |
Ap |
|
Au . |
|
|
|
|
|
|
|
|
|
|
|
(3.3) |
||||
Очевидно, |
о повній ро оті відповідає пло |
а пр |
окутника. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
л |
лінійно дефор овани систе |
|
іж навантаженн |
і пере |
і |
енн |
, |
о |
у |
овлене, |
існує |
|||||||||||||||
лінійна |
алежніст |
рис. |
. ,в . При ц о |
у дійсна ро ота |
о ражуєт с |
пло |
ею |
аштри овано о |
|||||||||||||||||||
трикутника. Очевидно, |
о додаткова ро ота в тако |
у ра і дорівнює дійсній ро оті |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
Ap |
Au |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
(3.4) |
|||
і оже |
ути о числена к пло а трикутника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
A |
P |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(3.5) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О начена |
рівніст |
на иваєт с |
|
теоремою |
Клапейрона |
|
|
|
- |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Отже, ро ота сили на |
у овлени |
цією силою пере і |
енн |
|
на иваєт с дійсною. |
к |
о ж |
||||||||||||||||||||
сила P, |
алишаючис |
не |
інною, дійснює ро оту на пере |
і енн |
|
l, |
у овлени |
інши |
и ді и, |
||||||||||||||||||
то таку ро оту на ивают |
можливою. |
ожлива ро ота дорівнює до утку величини сили на |
|||||||||||||||||||||||||
відповідне пере і енн , |
ке у овлене інши |
и сила |
и |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
A |
|
P |
l . |
|
|
|
|
|
|
|
|
|
|
|
|
(3.6) |
|||
|
л |
о численн |
ро оти внутрішні |
сил відокре |
и |
о нескінченно |
алий еле |
ент довжиною |
|||||||||||||||||||
dx. |
а рис. . ,а о ражено внутрішні |
усилл , |
|
кі діют |
у перері а |
еле |
ента. |
или N , M , |
Q дій- |
||||||||||||||||||
снювати |
ут |
ро оту відповідно на по довжні |
|
дефор |
аці |
, в ає |
ни |
кута |
повороту і в ає |
ни |
|||||||||||||||||
кута |
суву |
перері ів. |
і |
дефор аці |
о ражено |
на рис. . |
, |
. |
, |
. По довжн |
дефор |
аці |
|||||||||||||||
становит |
dx , де |
|
відносна |
по довжн |
|
дефор |
аці |
|
|
l |
l |
в ає ний кут повороту |
|||||||||||||||
d |
dx ( |
криви на осі дефор |
овано о стержн |
|
поперечна дефор аці |
dx , де |
кут |
||||||||||||||||||||
суву. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еорі перемі ен |
4 |
ис. .
ійсна ро ота внутрішні сил становити е
U |
1 |
( N dx |
M dx |
Q dx ). |
(3.7) |
|
|
||||||
2 |
||||||
|
l |
|
|
|
||
|
|
|
|
|
||
Анало ічно ожна аписати |
ожливу ро оту внутрішні сил одно о стану i на пере і |
енн |
||||
іншо о стану p: |
|
|
|
|
|
|
|
|
|
Uip |
( Ni pdx |
Mi pdx |
|
Qi pdx ). |
|
(3.8) |
||
|
|
|
|
l |
|
|
|
|
|
|
|
ци |
фор |
ула |
підсу овуванн |
поширюєт с |
на |
всі стержні |
систе и. нак |
інус |
|||
поставлено то |
у, |
о внутрішні |
сили |
стержнево |
систе |
и |
N ,M ,Q |
дл нескінченно |
ало о |
||
еле ента, |
кий вилучено і стержнево систе и, є |
овнішні |
и. Внутрішні ж сили в еле енті |
удут |
|||||||
ати ут |
таку са у величину, але спр |
овуют с |
у воротно |
у напр ку. |
|
||||||
3.2. Узагальнені сили і узагальнені переміщення
|
точки |
ору про ле |
, о |
вивчают с |
удівел ною |
е анікою, |
всі пере і |
енн |
лінійні |
|||||
пере |
і |
енн |
точок споруди, кути повороту перері ів в еле |
ента , в ає |
ні поступал ні і кутові |
|||||||||
пере |
і |
енн |
перері ів то |
о |
ают одні й ті са |
і властивості. |
о |
у |
а вичай |
уд - |
ке пере- |
|||
і енн , не алежно від |
йо о |
арактеру |
а о від |
причин, |
о |
йо о |
у овлюют , на ивают |
|||||||
узагальненим переміщенням, то то пере і |
енн |
у а ал но |
у ро у |
інні ц о о слова. |
|
|||||||||
еорі |
|
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
5 |
||||
|
ожно |
у пере і |
енню ставл т |
у відповідніст |
|
певну силову дію, |
ка |
дійснює ро оту на |
||||||||||
ц о |
у пере |
і |
енні. |
ака силова ді |
на иваєт с |
узагальненою силою, |
то то силовою дією в |
|||||||||||
а ал но |
у сенсі слова. |
і ни у а ал нени |
пере |
|
і |
енн |
відповідают |
рі ні а |
арактеро та |
|||||||||
напр |
ко |
у а ал нені сили. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
о л не |
о кіл ка прикладів у а ал нени |
пере |
і |
ен і відповідни |
ци сила |
у а ал нени |
||||||||||||
сил. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
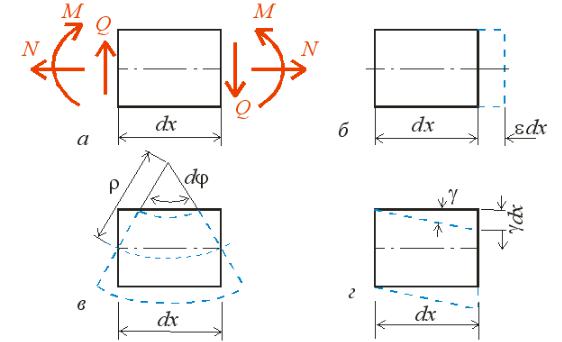
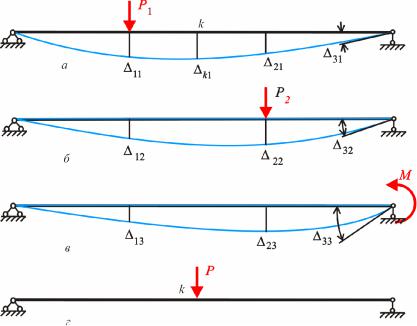
1. Внаслідок дефор |
аці споруди точка C пере |
|
істит с |
в положенн |
C1 |
рис. |
. |
,а . |
о ота |
|||||||||
сили P, |
ка |
|
оже |
ути прикладена в цій точці, |
вира ит с |
співвідношенн |
A |
P |
, |
де |
||||||||
відрі ок |
CC2 , |
кий є |
проекцією |
повно о |
пере |
і |
енн |
CC1 на |
напр |
ді |
сили. |
Отже, |
||||||
2. В ре ул таті дефор ацій споруди точки C і |
D пере іст т с в |
положенн |
C1 і |
D1 |
|
відповідно рис. . , . |
о ота дво сил P, кі ожут |
ути прикладені в ци |
точка |
і спр |
овані |
на устріч одна одній, |
уде виражена співвідношенн |
|
|
|
|
A P 1 P 2 P( 1 2 ).
Отже,
.
3. В ре ул таті дефор аці споруди перері C стержн повернет с на кут рис. . ,в . При ц о у осереджений о ент M, кий оже ути прикладений в ц о у перері і, дійснит ро оту
A M .
аки чино ,
.
ис.3.3
еорі |
перемі ен |
|
|
|
|
|
|
6 |
|
. шарнірі C поєднуют с |
два стержні. В процесі дефор |
аці один і |
стержнів повернет с |
на |
|||||
кут 1, а дру ий |
на кут 2 |
рис. . , . |
ва однакови а величиною і протилежно спр |
овани |
|||||
осереджени о |
енти M, кі ожут |
ути прикладені до кожно о |
і стержнів, при |
ц о |
у |
||||
дійснюют |
ро оту |
|
|
|
|
|
|
|
|
|
|
|
A M 1 |
M 2 |
M( 1 |
2 ). |
|
|
|
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
3.3. Універсальні позначення переміщень
Буд - ке у а ал нене пере і енн |
по начаєт с |
літерою |
, |
к |
о воно |
у |
овлене овнішн ою |
||||||||
дією довіл но величини, |
а о літерою , |
к |
о величина ді |
дорівнює одиниці. |
В по наченн |
||||||||||
ввод т с два індекси, наприклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3P , ik . |
|
|
|
|
|
|
|
|
|
ндекси по начают |
ісце на одженн |
і |
арактер |
пере |
і |
енн , а |
також |
дію, |
о йо о |
||||||
у овлює. Перший індекс пов |
аний |
арактеро |
та напр |
о |
пере |
і |
енн . Він вка ує на |
||||||||
у а ал нену силу, |
ка відповідає ци |
арактеристика . |
ру ий індекс пов |
аний і |
дією, ка |
||||||||||
викликає це пере і |
енн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
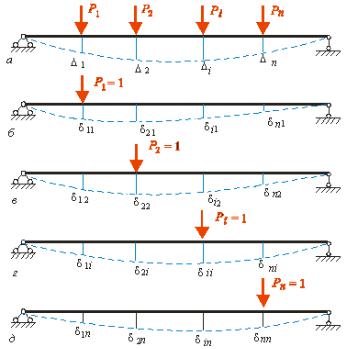
а рис. . ,а-в |
о ражено три |
дефор |
овани стани |
алки, |
|
о пере уває під дією рі ни |
|||||||||
навантажен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. .
еорі перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|||||
ак, |
12 |
вл є со ою пере |
і |
енн в напр |
і сили P1 |
першо о стану, то то про ин |
алки, від |
|||||||||||
ді сили |
P2 |
дру о о стану |
31 |
пере |
і енн |
в напр |
і сили P3 |
трет о о стану, |
то то кут |
|||||||||
повороту, від ді |
сили P1 першо о стану то |
о. |
в а алі |
ожна ска ати, |
о |
ij це пере |
і |
енн в |
||||||||||
напр |
і у а ал нено |
сили стану i від ді у а ал нено сили стану j. |
|
|
|
|
|
|
||||||||||
Отже, |
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
||
|
|
|
. |
ак, |
дл то о, |
о |
по начити в попередн о у прикладі вертикал не пере |
і |
енн |
|||||||||
точки |
k |
від |
ді сил стану |
, створи о |
допо іжний стан k, приклавши в перері і k |
|
алки |
|||||||||||
вертикал ну |
осереджену силу |
рис. . , . |
оді дане пере |
і |
енн по начати |
ет с |
k1 . |
|
|
|
||||||||
3.4. Матриця податливості і матриця жорсткості |
|
|
|
|
|
|
||||||||||||
о |
л не |
о |
ку-не уд стержневу систе |
у, наприклад |
|
алку, під дією кіл ко |
у а ал нени |
сил |
||||||||||
P1, P2 , , Pn |
рис. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а підставі принципу не алежності ді |
сил |
принцип суперпо иці |
уд - кий про ин |
|
ожна |
|||||||||||||
подати |
|
к су |
у про инів від кожно сили окре о |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
i |
i1 |
i2 |
|
|
in . |
|
|
|
|
|
(3.9) |
ручно вира ити дійсний про ин чере про ини, у овлені дією одинични сил
ис. .
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|||
|
|
|
|
|
|
i |
i1P1 |
i2P2 |
|
|
inPn , |
|
|
|
(3.10) |
|||
де ik |
пере |
і енн |
від ді сили |
Pk |
1, де k 1, 2, , n . Отже, |
ожна |
аписати |
|
|
|
||||||||
|
|
|
|
|
|
1 |
11P1 |
|
12P2 |
1nPn, |
|
|
|
|
||||
|
|
|
|
|
|
2 |
21P1 |
|
22 P2 |
2nPn, |
|
|
|
(3.11) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
n |
n1P1 |
|
n2P2 |
nnPn. |
|
|
|
|
||||
а о в |
атричній фор |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
B P , |
|
|
|
|
|
(3.12) |
||
ут |
по начено |
|
{ |
1 |
2 |
|
|
n} |
|
|
вектор |
у а ал нени |
пере |
і |
ен , |
|||
PT {P1 |
P2 |
Pn} |
вектор |
овнішні |
|
дій, |
B |
квадратна |
атриц |
одинични |
пере |
і |
ен , |
|||||
то то |
пере |
і |
ен , |
кі |
у |
овлені |
одинични и |
у а ал нени |
и сила |
и. а начена |
атриц |
|||||||
на иваєт с |
матрицею податливості: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
11 |
|
12 |
|
1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
21 |
22 |
2n . |
|
|
|
|
(3.13) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
n2 |
|
nn |
|
|
|
|
|
|
удь-який коефіцієнт матриці податливості ij характеризує величину переміщення в
напрямі i від дії в напрямі j одиничної узагальненої сили. |
|
|||||||
атрично |
рівності |
. |
ожна |
ати величини сил, |
кі відповідают одинични |
|||
у а ал нени пере |
і |
енн |
|
|
|
|
|
|
|
|
|
|
|
P |
B 1 |
K |
(3.14) |
ц о у вира і K |
B 1 |
квадратна |
атриц , ку на ивают матрицею жорсткості: |
|||||
|
|
|
|
|
k11 |
k12 |
k1n |
|
|
|
|
|
K |
k21 |
k22 |
k2n . |
(3.15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kn1 |
kn2 |
knn |
|
координатній фор і рівніст . |
ає ви л д |
|
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
||||
|
|
|
|
|
|
P1 |
|
|
k11 1 |
|
k12 2 |
|
|
k1n n , |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
P2 |
|
|
k21 1 |
|
k22 2 |
|
|
k2n n , |
|
|
|
|
(3.16) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Pn |
|
|
kn1 1 |
|
kn2 2 |
|
|
knn n . |
|
|
|
|
|
|
||||||
|
л |
ви наченн |
|
фі ично о |
|
істу |
коефіцієнтів |
атриці |
жорсткості |
покладе о |
в |
|||||||||||||||
|
співвідношенн |
. |
|
всі пере |
і |
енн , окрі |
одно о, |
таки и, |
о дорівнюют |
нулю. |
|
априклад, |
||||||||||||||
|
не ай |
1 |
3 |
|
4 |
…= |
n |
|
0 , |
а |
2 |
|
1. |
|
оді |
першо о |
рівн нн |
P1 |
|
k12 , то то |
||||||
|
коефіцієнт |
атриці |
жорсткості |
при |
а начени |
у |
ова |
дорівнює першій у а ал неній силі в |
||||||||||||||||||
|
напр |
і дру о о |
у а ал нено о пере |
і |
енн . |
в а алі |
ожна ска ати, |
о довільний коефіцієнт |
||||||||||||||||||
|
kij дорівнює силі |
Pi |
від |
дії |
|
примусового |
переміщення |
j |
1 за |
умови, |
що |
всі інші |
||||||||||||||
|
переміщення дорівнюють нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
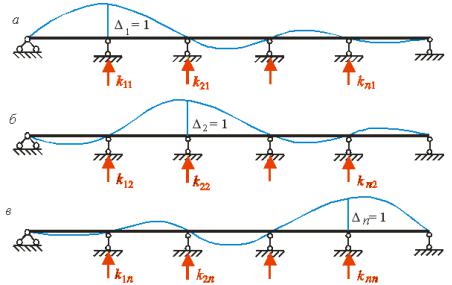
|
аки |
чино |
, еле |
енти |
атриці жорсткості |
ожна трактувати |
к опорні реакці |
в |
ей, |
о |
||||||||||||||||
|
накладені на систе у в напр |
|
і ожливи |
пере |
і |
ен |
рис. . . |
о |
у |
атрицю жорсткості |
||||||||||||||||
|
інколи на ивают |
|
атрицею реакцій. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. .
3.5. нтеграл Мора
ай а ал ніши |
етодо о численн |
пере |
і ен у стержневи систе |
а |
є |
етод ора. Він |
випливає принципу |
ожливи пере і |
ен |
і до вол є ви начати пере |
і |
енн |
точок систе и |
чере усилл в еле |
ента . |
|
|
|
|
|
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
||||
Принцип |
ожливи пере і ен , |
кий сфор |
ул овано |
а ранже |
дл |
систе |
, складени |
|
тіл, |
||||||||||||||
о не дефор |
уют с , є фунда |
ентал ни |
принципо |
е аніки. |
ідно |
ци |
принципо |
дл |
уд - |
||||||||||||||
ко |
рівноважено |
систе |
и |
су а |
ро іт |
всі |
прикладени |
овнішні |
|
сил на |
віртуал ни |
||||||||||||
пере |
і енн |
дорівнює |
нулю. |
л |
пружни |
систе |
о начений |
|
принцип |
|
оже |
|
ути |
||||||||||
сфор |
ул ований таки |
чино |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
то то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
U |
0 . |
|
|
|
|
|
|
|
|
|
(3.17) |
|||
ц о |
у вира і A |
|
ро ота |
овнішні , |
а U |
внутрішні |
сил. |
овнішні сили |
це навантаженн , |
||||||||||||||
о прикладені до конструкці , та опорні реакці , внутрішні |
це |
|
усилл , |
кі |
виникают |
в |
|||||||||||||||||
еле ента |
споруди при |
дефор уванні. |
ожливи и вважают с |
пере |
і |
енн , |
кі припускают с |
||||||||||||||||
існуючи |
и в |
и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
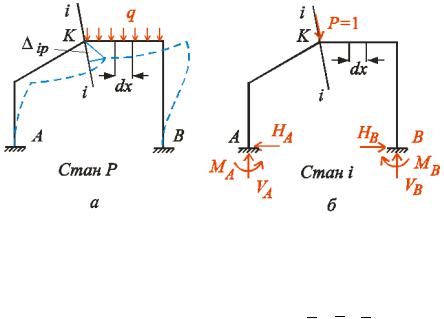
о |
л не |
о два напружено-дефор |
овани |
стани стержнево |
систе |
|
и. Перший стан |
рис. |
. |
,а |
|||||||||||||
у овлено овнішні |
и навантаженн |
и, |
кі, по суті, |
ожут |
ути довіл ни |
и. |
а ве |
о цей напру- |
|||||||||||||||
жено-дефор |
ований стан стержнево систе и вантажним, а о стано |
P. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
ис. . |
|
|
|
|
|
|
|
|
дру о |
у стані на стержневу систе |
у в довж де ко |
довіл но пр |
о i-i діє одна |
осереджена |
|||||||
сила, |
ка дорівнює одиниці. |
акий стан |
стан i |
уде |
о на ивати допоміжним, а о одиничним. |
||||||||
Внутрішні |
усилл |
допо іжно о стану по начати |
е |
о |
к Mi , Qi , Ni . О идва ці стани є |
ож- |
|||||||
ливи |
и і, |
ідно |
принципо |
а ранжа, су |
а ро іт одно о стану на пере |
і енн |
іншо о |
ає |
|||||
дорівнювати нулю. |
о л не |
о ожливу ро оту сил стану i на пере і |
енн |
стану P: |
|
|
|||||||
|
|
|
|
Aip |
Uip |
0 . |
|
|
|
|
(3.18) |
||

|
еорі |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
||||||
|
|
ожлива |
ро ота |
овнішні |
сил |
дорівнює |
до утку |
одинично |
сили |
стану |
на відповідне |
||||||||||||||||||||||||||||
|
пере |
і енн |
стану P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aip |
1 |
|
ip . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.19) |
|||||
|
Підстави |
о |
ро оту |
овнішні |
|
сил |
. |
|
|
|
і |
ожливу |
ро оту |
|
внутрішні |
|
сил |
3.8 |
у |
||||||||||||||||||||
|
співвідношенн . . |
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ip |
|
|
|
(Ni pdx |
Mi pdx |
|
Qi pdx). |
|
|
|
|
|
(3.20) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
фор ула, посутн о, є на лиженою, оскіл ки пере |
і |
енн |
|
реал ни |
систе |
ают |
|||||||||||||||||||||||||||||||
|
скінченні |
наченн . |
и |
еншу величину становл т |
пере |
і енн , ти |
|
фор |
ула точніша. Проте |
||||||||||||||||||||||||||||||
|
оскіл ки |
жорсткості |
еле |
|
ентів реал ни |
споруд |
достатн о |
|
великі, |
цю |
фор |
улу |
ожна |
||||||||||||||||||||||||||
|
ро |
л дати |
к |
точну. |
а |
, |
де |
точніст |
ви вл єт с недостатн ою, |
|
ожут |
|
ути |
астосовані |
|||||||||||||||||||||||||
|
етоди ро в |
|
анн |
ео |
етрично нелінійни |
адач. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
При ді |
на споруду неру о о о |
овнішн о о навантаженн |
дефор |
аці |
ожут |
|
ути виражені |
|||||||||||||||||||||||||||||||
|
чере |
внутрішні сили. |
л фі ично-лінійни |
систе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
N p |
|
, |
p |
|
|
1 |
|
|
M p |
|
, |
p |
|
|
Qp |
|
, |
|
|
|
|
|
(3.21) |
||||||
|
|
|
|
|
|
|
|
|
EA |
|
|
p |
|
|
EI |
|
|
GA |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
де |
е ро |
ірний коефіцієнт, |
о |
алежит |
|
від фор |
и перері у стержн |
|
і о числюєт с |
а |
||||||||||||||||||||||||||||
|
фор |
улою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
Sвідс |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.22) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
dA. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
Ixby |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
окре а, дл |
пр |
окутно о перері у =1,2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
ура уванн |
|
. |
|
фор |
ула дл |
о численн |
|
пере і |
ен |
. |
|
на ирає ви л ду |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
ip |
|
|
|
|
Ni NP dx |
|
|
Mi MP dx |
|
|
|
QiQP dx. |
|
|
|
(3.23) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
|
|
|
|
|
EI |
|
|
|
|
|
GA |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
ей вира |
на иваєт с |
фор улою Максвелла–Мора. |
а допо |
о ою ціє |
фор |
ули |
ожна |
||||||||||||||||||||||||||||||
|
о числити |
|
уд - |
ке пере і |
|
енн |
в |
|
уд - |
кій стержневій систе |
і чере |
|
внутрішні |
усилл |
дво |
|
|||||||||||||||||||||||
|
станів. Перший |
стан |
|
вантажний |
|
у |
овлено |
дією |
овнішні |
|
навантажен , дру ий |
|
|||||||||||||||||||||||||||
|
допо іжний |
|
|
дією |
одинично |
|
у а ал нено сили, |
ка |
|
відповідає |
пере |
і |
енню, |
о |
|||||||||||||||||||||||||
|
ро шукуєт с . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еорі |
перемі ен |
|
|
|
|
12 |
|||||||
аки |
чино , дл |
о численн |
уд - ко о пере і |
енн |
нео ідно |
||||||||
Ви начити усилл |
M p , N p ,Q p від |
овнішн о о навантаженн . |
|||||||||||
О рати |
допо іжний стан i, |
відкинувши |
овнішні |
навантаженн і приклавши одиничну |
|||||||||
у а ал нену силу, |
о відповідає пере і енню. |
|
|
||||||||||
Ви начити усилл |
|
|
i , |
|
|
|
|
|
|
|
|
||
|
M |
N |
i ,Qi |
у допо |
іжно |
у стані. |
|
||||||
О числити пере і |
енн а фор |
улою |
аксвелла- |
ора |
3.23). |
||||||||
3.6.кремі випадки застосування формули Максвелла–Мора
Величини кожно о |
тр о |
доданків у фор |
|
улі |
|
|
аксвелла– |
|
ора |
арактери уют |
внесок то о |
||||||||||||||||
чи іншо о виду внутрішні |
усил |
в пере |
і |
|
енн , |
о ро шукуєт с . а підставі аналі у ци |
|||||||||||||||||||||
доданків ожна дійти висновку, |
о дл |
рі но о виду конструкцій не туванн де ки и вида и |
|||||||||||||||||||||||||
усил |
ало по начаєт с |
на величині пере |
|
і |
|
|
енн . |
ак, дл |
|
алок і ра , дефор |
уванн ки |
||||||||||||||||
від уваєт с |
переважно |
а ра унок |
ину, |
ожна |
не тувати впливо |
|
по довжні |
і поперечни |
|||||||||||||||||||
сил. |
тако |
у ра і фор |
ула |
аксвелла– |
ора |
|
|
|
|
ати |
е ви л д |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i M P |
dx . |
|
|
|
|
|
|
|||||
|
|
|
|
|
ip |
|
M |
|
|
|
|
|
(3.24) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
піввідношенн . |
|
на ивают |
інтегралом Мора. |
|
|
|
|
|
|
|
|||||||||||||||||
л |
фер |
, в стержн |
|
ки |
існуют по довжні дефор |
аці , ожна аписати |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i NP |
dx. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ip |
|
|
N |
|
|
|
|
|
(3.25) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|||
л |
арок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i NP |
dx |
|
|
|
i M P |
dx. |
|
||||||
|
|
|
|
|
|
ip |
|
|
|
|
|
N |
|
M |
(3.26) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
l |
|
EA |
|
|
|
|
l |
|
EI |
|
|
|
||||||||
3.7.бчислення інтеграла Мора
нте рал |
ора оже ути о числений а о е посередні |
інте руванн , а о а допо о ою |
|
прийо ів чисел но о інте руванн . В практични |
адача , к правило, використовуют два прийо- |
||
и чисел но о інте руванн правило Верещагіна і формулу |
імпсона– Корноухова. Процедура |
||
о численн |
інте рала ора в тако у ра і на ивают |
множенням епюр. |
|
еорі перемі ен |
13 |
||||||
|
|
|
|
l |
|
||
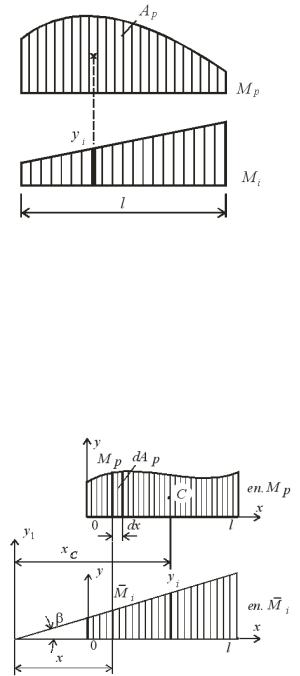
а правило Вере а іна дл о численн інте рала |
|
i M p dx достатн о по |
ножити пло у |
||||
M |
|||||||
0 |
|
|
|
||||
епюри M P на ординату епюри |
|
i , о ерет с під центро т жінн епюри M P |
рис. . |
||||
M |
|||||||
|
|
l |
|
||||
|
|
|
|
i M pdx Ap yi . |
(3.27) |
||
|
|
M |
|||||
0 |
|
|
|
|
|
||
|
|
|
|
ис. . |
|
|
|
|
к |
о ордината yi |
і пло |
а Ap ро ташовані по один і той са ий ік стержн , до уток ерет с |
|||||
і нако |
плюс . |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
||
асправді, |
ро л не о о численн інте рала |
|
|
i M Pdx на прикладі пере |
ноженн дво |
|||
M |
||||||||
|
|
|
|
|
0 |
|
|
|
епюр рис. . |
, одна |
ки |
M P ає довіл ний арактер, а дру а – Mi о ежена пр |
ою. |
||||
ис. .
о уток M Pdx є еле ентарною пло ею, ка ерет с на епюрі M P :

еорі перемі ен |
14 |
dAP M Pdx .
Ординату на пр |
олінійній епюрі |
ожна представити у ви л ді Mi |
x tg . |
рештою інте рал |
|||||||||||||||||
на уває ви л ду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
l |
|
|
|
l |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
MiM Pdx |
x tg dAP |
tg |
xdAP . |
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
||
нте рал у правій частині співвідношенн |
|
це статичний о |
ент |
SP пло |
і епюри M P |
||||||||||||||||
стосовно осі y1, |
ка про одит |
чере |
точку перетину |
епюри |
|
|
i |
пр |
ою, |
о |
і аєт с |
||||||||||
M |
|||||||||||||||||||||
віссю |
стержн . |
к відо о, статичний |
|
о ент пло |
і дорівнює до утку пло |
і на координату |
|||||||||||||||
центра |
т жінн |
SP |
AP xC . |
а цій підставі |
ає |
о |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MiMPdx xC AP tg . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нарешті, по |
ітивши, |
о xCtg |
yi , остаточно одержує о |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i M Pdx |
AP yi . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ор |
ула |
і псона– |
орноу ова – це окре |
ий випадок відо |
о |
ате |
атично о аналі у |
|||||||||||||
фор ули і |
псона |
фор ули |
пара ол |
|
дл |
о численн |
ви начени |
інте ралів, коли інтервал |
|||||||||||||
інте руванн |
ро кладаєт с |
на дві діл нки рис. . |
|
|
|
|
|
|
|
|
|
|
|||||||||
ис. .
еорі перемі ен |
|
|
|
|
|
|
|
|
|
15 |
l |
|
|
|
l |
|
|
|
|
|
|
M |
M |
|
dx |
a a |
|
4c c |
|
b b |
(3.28) |
|
i |
|
P |
|
6 |
i |
p |
i |
P |
i P |
|
0 |
|
|
|
|
|
|
|
|
|
|
При використанні фор ули |
і |
псона– |
орноу ова нео |
ідно, |
о |
|||||
|
|
|
|
|
|
|
|
|
В |
|
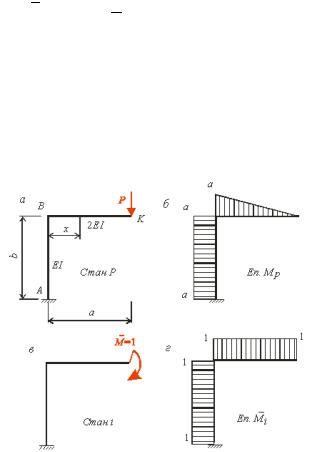
Приклад 3.1. О числити кут повороту в перері і k ра и рис. . ,а .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Процес ро в анн |
істит |
чотири етапи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1. |
Ви наченн |
усилл |
від |
овнішн о о |
навантаженн . |
|
|
|
а ри елі M p |
P( a |
x ), на стійці |
|||||||||||||||||||||||||||||||
|
M p Pa. Епюру |
M p |
по удовано на рис. . |
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2. |
творенн |
допо |
іжно о стану. опо |
іжний стан |
стан i |
|
о ражено на рис. |
|
. ,в. |
|||||||||||||||||||||||||||||||||
3. |
Ви наченн |
усил |
в допо |
іжно |
у стану на ри елі |
|
|
|
i |
1, на сто ку |
|
|
i |
1. Епюру |
|
i |
||||||||||||||||||||||||||
M |
M |
M |
||||||||||||||||||||||||||||||||||||||||
|
по удовано на рис. |
. |
|
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. |
О численн |
пере |
і |
енн |
а фор |
улою |
|
ора. е |
ожна |
ро ити в рі ні спосо и. |
|
|
|
|
||||||||||||||||||||||||||||
|
езпосереднє інтегрування: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
i M P |
dx |
B |
|
|
i M P |
dx |
K |
|
|
|
i M P |
dx |
|
|
|
|
|
|
|
|
||||||||||||||
|
ip |
|
|
M |
M |
M |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
l |
|
|
|
EI |
|
|
|
|
A |
EI |
B |
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
= |
b 1 Pa |
|
a P( a |
|
x ) 1 |
Pab |
|
|
|
Pa2 |
|
|
Pa2 |
Pa |
|
|
|
a |
||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
. |
|
|
||||||||||
|
|
0 |
|
EI |
|
|
0 |
|
|
2EI |
|
|
|
EI |
|
|
|
2EI |
|
|
4EI |
EI |
|
4 |
|
|
||||||||||||||||

еорі перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
||
За правилом Верещагіна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ip |
|
MiMP |
dx |
B |
MiMP |
dx |
K |
MiM P |
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
l |
EI |
|
|
|
A |
|
EI |
B |
|
2EI |
|
|
|
|
||||
|
1 |
( Pa b ) |
1 |
|
|
1 |
|
1 |
Pa a |
1 |
|
Pa |
|
b |
a |
. |
||||
|
EI |
|
|
|
|
|
EI |
4 |
||||||||||||
|
|
|
|
|
2EI |
2 |
|
|
|
|
|
|
|
|||||||
За формулою імпсона–Корноухова:
ip |
MiM P |
dx |
B |
MiMP |
dx |
||||||||
|
|
|
|||||||||||
|
|
l |
|
EI |
A |
EI |
|
|
|||||
|
|
b |
|
1 Pa 4 1 Pa |
1 |
Pa |
|||||||
|
6EI |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a |
|
Pa 1 |
4 |
Pa |
1 |
0 |
|||||
|
|
6 2EI |
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|||||
K MiMP dx
B 2EI
Pa |
b |
a |
|
|
EI |
4 . |
|||
|
||||
3.8. Переміщення від дії температури
к відо о |
фі ики, |
тіла при на ріванні ро ширюют с , а при о олодженні |
скорочуют с . |
|||||
о у ді на споруду те |
ператури спричин є дефор уванн |
конструкцій. При ц о |
у в статично |
|||||
ви начувани |
систе а |
ані внутрішні |
усил , ані опорни |
реакцій не виникає. А відтак фор ула |
||||
ора у ви л ді . |
непридатна дл |
о численн те |
пературни пере і ен |
і виникає потре а |
||||
ати е один варіант фор ули, при начений власне дл |
ро ра унків на дію те |
ператури. |
||||||
апише о інте рал |
|
ора у ви л ді, |
кий є анало ічни |
. |
|
|
||
|
|
|
|
it |
|
(Ni tdx |
Mi t dx |
Qi t dx). |
(3.29) |
|||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
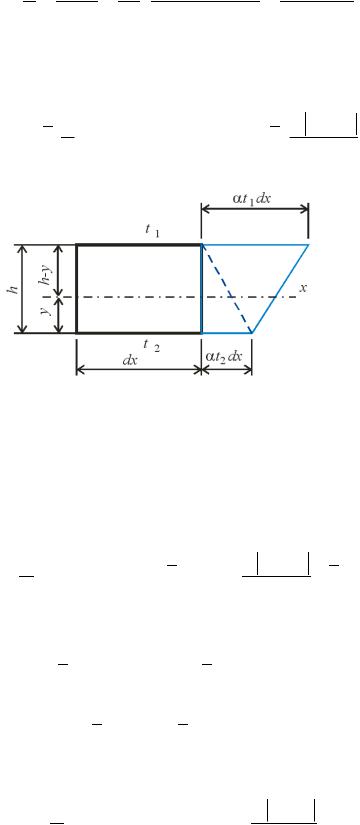
Вира и |
о дефор |
аці |
нескінченно |
ало о еле |
ента |
рис. . |
|
від ді |
те ператури. |
|||||
Припусти о дл |
о наченості, |
о t1> t2 > 0. |
оді видовженн |
вер н о о волокна становити е |
||||||||||
t1dx, а нижн о о |
t2dx, де |
коефіцієнт лінійно о |
ро ширенн |
атеріалу дл сталі і дл |
||||||||||
етону |
1,2 10-5 |
рад-1). |
|
|
|
|
|
|
|
|
|
|||
Відносне видовженн |
осі еле ента стержн |
|
|
|
|
|
|
|||||||
|
|
t |
|
t1dx |
y |
t2dx |
|
|
|
|
|
|
||
|
|
|
|
|
|
( h |
y ) |
|
t1 y |
t2 ( h |
y ) , |
|||
|
|
|
hdx |
hdx |
h |
|||||||||
еорі перемі ен |
|
|
|
|
|
17 |
криви на |
|
|
|
|
|
|
t |
1 |
dx |
1 t1dx |
t2dx |
(t1 t2 ) |
, |
|
|
dx |
dx |
h |
h |
|
кут суву t=0.
аки чино ,
l |
N |
|
t y |
t |
(h y) dx |
l |
M |
|
t1 t2 |
dx . |
(3.30) |
it |
|
i h |
1 |
2 |
|
|
|
i |
h |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. . |
|
|
|
|
|
|
|
||
Оскіл ки в ра |
а |
|
инал ні |
о |
енти не |
ают |
наків, у дру о |
у доданку рі ниц |
те ператур |
|||||||||||
ерет с а |
одуле |
, |
і до уток |
ерет с |
|
і |
нако |
плюс, |
к о ро т |
нені волокна на стержні в |
||||||||||
допо іжно |
у стані |
|
і ают с |
ро т нени |
и |
волокна |
и від ді |
те |
|
ператури. к |
о постійні |
|||||||||
величини винести |
а |
нак інте рала, одержи |
о |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
t y |
t |
|
(h |
|
|
y) |
l |
N |
dx |
t1 |
t2 |
l |
M |
dx . |
(3.31) |
|
|
|
it |
h |
1 |
|
2 |
|
|
|
|
|
i |
|
2 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
По начи |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
ANi |
Nidx, |
|
|
AMi |
Midx , |
|
|
|
|
(3.32) |
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
де AMi, ANi |
відповідно пло і епюри Mi |
і епюри Ni на стержні в допо |
іжно у стані. |
|||||||||||||||||
ура уванн |
по начен . |
остаточно |
ає |
о |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
t y |
|
t |
|
(h |
|
y) |
A |
t1 |
t2 A . |
(3.33) |
||||
|
|
|
|
it |
h |
1 |
|
|
|
2 |
|
|
|
Ni |
2 |
|
|
Mi |
|
|
еорі |
перемі ен |
|
|
|
|
|
|
18 |
В окре |
о у випадку, к о перері |
стержн |
си етричний, то то y=h/ , вира . |
на ирає |
||||
ви л ду |
|
|
|
|
|
|
|
|
|
it |
t1 |
|
t2 A |
|
t1 t2 A . |
(3.34) |
|
|
|
2 |
Ni |
|
h |
Mi |
|
|
|
|
|
|
|
|
|
||
ра і, коли еле енти споруди піддают с рівно ірно у на ріванню а о о олодженню, то то t1=t2=t, ає о
|
|
|
|
|
it |
tANi . |
(3.35) |
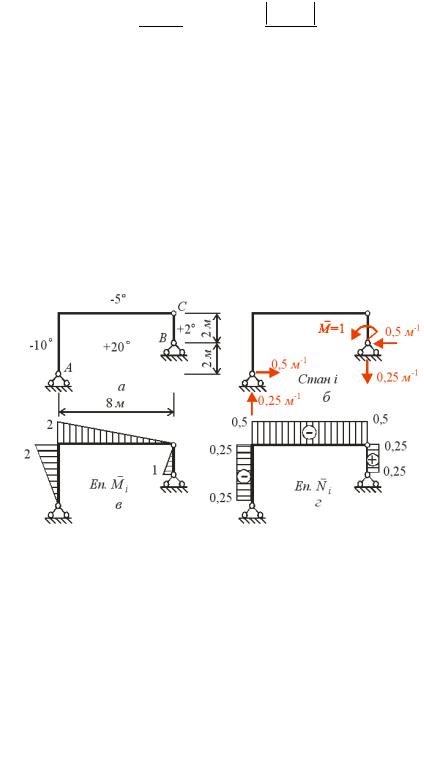
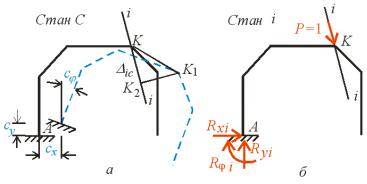
Приклад 3.2. О числити кут повороту в шарнірі B ра и, ка пере уває під дією те |
ператури |
||||||
рис. . |
,а . |
тержні ра и |
ают |
пр |
окутний перері . Висота перері у сто ків становит |
, , а |
|
ри ел |
, |
. атеріал |
алі о |
етон |
=1,2 10-5 рад-1). |
|
|
|
|
|
|
|
|
ис. . |
|
|
опо |
іжний стан утворюєт с |
шл |
о |
прикладанн |
одинично о осереджено о о енту до |
|||
опори B. |
е у авантаженн |
й опорни |
реакцій у допо |
іжно у стані о ражено на рис. . |
, . |
|||
Відповідні епюри |
инаючи |
о |
ентів і по довжні сил по удовано на рис. . ,в і рис. . |
, |
||||
відповідно. Пере і |
енн о числює о |
а фор улою . |
|
|
||||
it 1,2 10 |
5 |
|
|
10 |
20 |
|
1 |
2 4 |
5 |
20 |
1 |
|
2 8 |
|
|
20 |
2 |
|
|
1 |
1 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0,2 |
|
|
2 |
0,4 |
2 |
|
0,2 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1,2 10 5 |
10 20 |
0,25 4 |
|
|
5 20 |
0,25 8 |
20 2 |
0,25 |
2 |
|
0,0123 р 1 . |
|||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
еорі перемі ен |
|
19 |
|
3.9. Переміщення від примусового зміщення опор |
|||
к |
о опори споруди |
і уют с , то споруда |
інює своє ро ташуванн , а точки одержуют |
пере і |
енн . При ц о у неважко впевнитис |
у то у, о в статично ви начувани систе а |
|
опорні реакці , внутрішні |
усилл і дефор аці еле ентів дорівнюют нулю. |
||
|
|
|
|
|
|
|
|
|
|
|
ис. . |
|
|
|
|
|
|
|
|
|
|
|
|
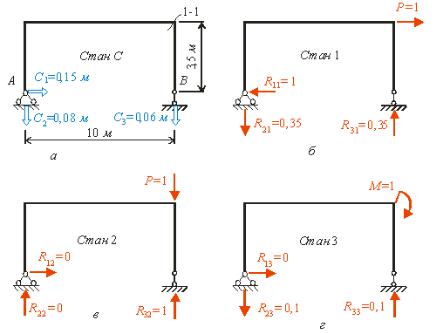
л |
о численн |
ко ос |
пере і |
енн , |
у овлено о |
і |
енн |
опор споруди, |
скористає |
ос |
|||||||||||||
принципо |
ожливи |
пере |
і |
ен . |
о |
л не |
о два ожливи |
стани споруди. |
|
|
|
|
|||||||||||
Перший стан C див.рис. . |
,а |
у |
овлено поступал ни |
|
и пере |
і |
енн |
и |
атисненн |
cx |
і cy |
||||||||||||
в напр |
і координатни |
осей і поворото |
на кут c . |
к вже |
адувалос , дефор аці еле |
ентів у |
|||||||||||||||||
ц о у стані не виникают . |
|
допо іжно у стані i |
див. |
|
рис. . |
, |
на ра |
у в напр |
і i-i діє |
||||||||||||||
одинична |
осереджена сила, |
ка спричинює опорні реакці |
Rxi, Ryi |
і R i. |
о |
л не |
о ро оту сил |
||||||||||||||||
стану i на пере |
і енн стану C. |
ідно |
принципо |
ожливи |
пере |
і ен |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Aic |
U ic |
0 |
|
|
|
|
|
|
|
|
|
(3.36) |
||
ефор |
аці |
в стані C відсутні, то |
у ро ота внутрішні |
сил Uic=0. Отже, |
|
. |
одержує о, |
||||||||||||||||
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aic |
0. |
|
|
|
|
|
|
|
|
|
|
(3.37) |
|
іншо о оку, ро ота |
овнішні |
сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Aic |
1 |
ic |
Rxi |
cx |
Ryi |
cy |
|
R i c . |
|
|
|
|
(3.38) |
|||||
а підставі |
. |
і . |
|
|
ожна |
аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ic |
Rxi |
cx |
Ryi |
cy |
R i |
|
c , |
|
|
|
|
|
|
(3.39) |
|||
а о в |
а ал но |
у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ic |
|
|
R jic j . |
|
|
|
|
|
|
|
|
(3.40) |
||
еорі |
перемі ен |
20 |
ц о |
у вира і R ji |
опорна реакці Rj допо іжно о стану i, c j відповідне ви ушене |
і енн |
опори у стані C. |
|
|
|
|
|
|
|
|
|
|
ис. . |
|
|
|
|
|
|
аки |
чино , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад |
3.3. |
Ви начити |
поступал ні |
пере |
і енн |
і |
кут повороту |
перері у - ра и |
|||||||
рис. . |
,а , |
о у |
овлюют с |
пере |
і |
енн |
и опор. |
|
|
|
|
|
|||
л |
о численн |
|
вертикал но о |
і |
ори онтал но о пере |
і |
ен , |
а також дл кута повороту |
|||||||
перері у |
– |
створює |
о допо |
іжні стани рис. . |
, – ). |
а ци |
с е |
а о ражено опорні реакці |
|||||||
ци станів. О числи |
о пере і |
енн |
|
а фор |
улою . |
|
|
|
|
|
|||||
ори онтал не пере |
і енн |
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1C |
|
R j1C j |
1 0,15 |
|
0,36 |
0,08 |
0,35 |
0,06 |
|
0,1422 |
; |
||||
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
вертикал не пере |
і |
енн |
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2C |
|
R j2C j |
|
1 0,06 0,06 ; |
|
|
|
|
|
|
|||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кут повороту
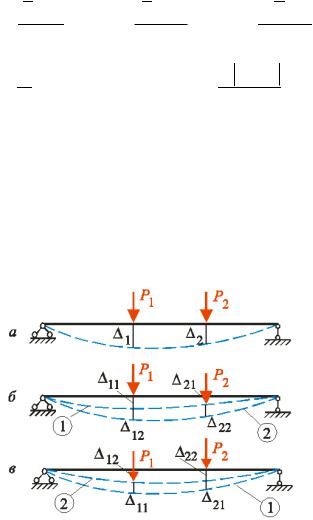
еорі |
перемі ен |
|
21 |
|
3 |
|
|
3C |
R j3C j |
0,1 0,08 0,1 0,06 |
0,02 р . |
j1
3.10.Повна формула для обчислення переміщень
|
практични |
ро ра унка |
ожливі випадки, коли |
стержневі |
систе |
и |
пере увают під |
|||||||||||
одночасною дією |
овнішні |
сил, при |
усово о пере |
і |
енн |
опор, а також те |
пературно о пол . В |
|||||||||||
ц о |
у ра і повне пере |
і |
енн |
оже |
ути ви начене на підставі принципу суперпо иці |
к су а |
||||||||||||
пере |
і ен |
від кожно |
ді |
окре |
о |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
iS |
ip |
it |
ic . |
|
|
|
|
|
|
|
Проте |
ожна скористатис |
не окре и и фор |
ула |
и пере і |
ен |
від окре |
и |
дій, а повною |
||||||||||
фор |
улою |
ора, |
ка |
оже |
ути аписана |
к су |
а пере |
і ен |
від силови |
|
дій |
3.23 , |
впливу |
|||||
те ператури 3.33 і при усово о пере і енн опор 3.40):
Ni NP dx |
|
MiM P dx |
|
QiQP dx |
|
|
|
|
|
iS |
EA |
|
EI |
|
GA |
|
|
|
|
l |
l |
l |
|
|
|
(3.41) |
|||
t y t |
(h y) A |
t1 t2 A |
R |
|
c |
. |
|||
h |
1 2 |
|
Ni |
2 |
Mi |
|
ji |
j |
|
3.11. Теореми взаємності
3.11.1.Теорема про вза мність робіт теорема Бетті
о л не |
о лінійно-дефор івну |
систе у, наприклад алку, під дією дво статично |
прикладени |
у а ал нени сил P1 i P2 |
рис. . . |
ис. .
еорі перемі ен |
22 |
Повні про ини алки під сила и від одночасно ді о о сил на підставі принципу суперпо иці ожна представити к су и про инів від ді кожно сили окре о
1 |
11 |
12 , |
2 |
21 |
22 . |
інцева дефор аці рис. . ,а не алежит |
від чер овості прикладанн сил, отже, ро л не о |
|
два спосо и авантаженн
1.початку до алки статично прикладаєт с сила P1 рис. . , , ка викликає про ини 1 і
виконує дійсну ро оту
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
1 |
P |
|
|
, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
1 |
11 |
|
|
|
|
|
|
|
|
|
|||||
а поті |
до дефор |
овано |
с е |
и прикладаєт с |
|
сила |
|
|
P2 . рештою |
алка одержує додаткові |
|||||||||||||||||||
про ини 2, і дійсну ро оту при ц о |
у виконує сила P2 : |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
1 |
P |
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
2 |
22 |
|
|
|
|
|
|
|
|
|
|||
а |
наченн |
ци |
додаткови |
про инів сила |
|
P1 |
не впливає, |
оскіл ки |
величина |
алишаєт с |
|||||||||||||||||||
не |
інною. |
о |
у ро ота |
є |
ожливою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
A12 |
|
P1 12 . |
|
|
|
|
|
|
|
|
|
|
|||||||
Повна ро ота, |
ку |
дійснюют |
о идві сили |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
A |
A |
|
A |
A |
|
1 |
P |
|
|
|
|
1 |
P |
|
|
P |
|
. |
|
|||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
11 |
|
22 |
12 |
|
1 |
|
11 |
|
2 |
22 |
1 |
12 |
|
|
|||||||||
2. початку до |
алки прикладаєт с |
сила P2 |
(рис. |
. |
,в ,. Вона викликає про ини 2 і дійснює |
||||||||||||||||||||||||
дійсну ро оту A22 . Післ |
ц о о до дефор |
|
овано |
с е |
|
и статично прикладаєт с сила P1. Балка |
|||||||||||||||||||||||
одержує додаткові про ини 1. |
о ота A11, |
|
|
|
ку виконує ц |
сила, |
також уде дійсною. При |
||||||||||||||||||||||
ц о |
у |
величина |
сили |
P2 |
алишаєт с |
не |
|
|
|
інною, |
|
а |
відтак |
на |
величини ци |
додаткови |
|||||||||||||
про инів не впливає. Отже, |
ро ота A21 |
повинна ро |
|
л датис |
к |
ожлива |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A21 |
|
|
P2 |
|
21 . |
|
|
|
|
|
|
|
|
|
|||||
Повна ро ота в ц о у випадку |
ати е ви л д |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
еорі перемі ен |
23 |
A A |
A |
A |
1 |
P |
|
|
1 |
P |
|
P |
|
. |
|
2 |
|
2 |
|
|
|||||||||
22 |
11 |
21 |
|
2 |
22 |
1 |
11 |
2 |
21 |
|
|||
Порівнюючи повну ро оту в о о |
випадка |
до оди |
о висновку, |
о |
|
|
|||||||
|
|
P1 |
12 |
|
P2 |
21 . |
|
|
|
|
(3.42) |
||
|
|
|
A12 |
A21 . |
(3.43) |
|
Положенн , |
ке ойно уло доведене, відо |
е під на вою теореми про взаємність робіт, а о |
||||
теореми |
етті. |
|
|
|
|
|
3.11.2.Теорема про вза мність переміщень теорема Максвелла |
|
|||||
к о в . |
покласти, о P1 |
P2 P , ати |
е |
о |
|
|
|
|
|
12 |
|
21 . |
|
оли, до то о ж, у а ал нені сили дорівнюют |
одиниці P1 P2 |
1, то |
||||
|
|
|
12 |
21. |
(3.44) |
|
івніст |
. |
виражає теоре |
у про в ає ніст |
пере і ен |
|
|
.
теоре и про в ає ніст пере і ен , ка також відо а к теоре а аксвелла, випливає, о атриц податливості див. п. . .)
11 12 1n
B21 22 2n
n1 n2 nn
є си етричною стосовно оловно діа оналі.
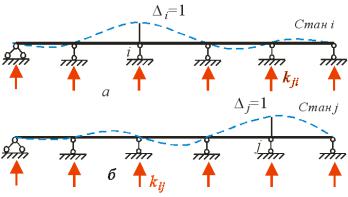
еорі перемі ен |
|
|
|
|
|
|
24 |
|||
3.11.3.Теорема про вза мність реакцій |
теорема Релея |
|
|
|
||||||
о |
л не |
о |
дл прикладу |
пружну |
систе |
у у ви л ді |
суціл но |
а атопро оново |
алки |
|
рис. . |
у |
дво |
стана |
та |
j, у овлени |
при усови |
и пере і |
енн и опор |
i та j |
|
відповідно.
|
|
|
|
|
ис. . |
|
|
|
|
|
В о о |
стана |
алка ви инаєт с |
і на |
опора |
виникают |
опорні реакці , кі по начи о |
kij |
|||
реакці на опорі i в стані j, k ji реакці |
на опорі j в стані i. |
оді |
теоре и про в ає ніст |
ро іт |
||||||
випливає, |
о |
|
|
|
|
|
|
|
|
|
|
|
|
kij |
i k ji |
j . |
|
|
|
||
к о пере і |
енн опор дорівнюют |
одиниці |
i |
1, j |
1 , |
ає о |
|
|||
|
|
|
|
kij |
k ji . |
|
|
|
|
(3.45) |
Отже |
|
і |
|
|
|
|
|
|
j |
|
|
|
|
j |
|
|
|
|
|
і. е положенн |
|
на ивают |
теоре |
ою про в ає ніст |
реакцій. |
а підставі теоре и . |
ожна дійти до висновку, |
|||||
о атриц |
жорсткості пружно систе и |
див. п. . |
). |
|
|
|
||||
|
|
|
|
k11 |
k12 |
|
k1n |
|
|
|
|
|
|
K |
k21 |
k22 |
|
k2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kn1 |
kn2 |
|
knn |
|
|
|
авжди си етрична відносно оловно діа оналі.
3.11.4.Теорема про вза мність реакцій і переміщень
о л не о таку са у суціл ну а атопро онову алку в інши одинични стана рис. . .
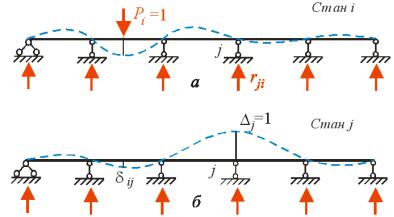
еорі |
перемі ен |
25 |
|
стані |
до |
алки прикладена одинична осереджена сила Pi |
1 рис. . ,а , а в стані j |
при усово пере і |
уєт с опора j рис. . , . |
|
|
|
|
ис. . |
|
|
|
|
а підставі теоре и Бетті ожна |
аписати |
|
|
|
|
|
|
|
Aij |
Aji . |
|
|
|
Однак ро ота Aji , оскіл ки |
сила и у |
стані |
j |
є опорні реакці , а |
опори стану не |
|
пере і уют с . Отже, ро ота сил стану |
на пере |
і енн |
стану j також дорівнює нулю |
|||
|
Aij |
Pi ij |
rji |
j |
0 . |
|
відси |
|
|
|
|
|
|
|
|
rji |
ij . |
|
(3.46) |
|
j |
|
|
|
|
Pi |
1 |
|
|
|
|
|
|
Pi 1 |
|
j. |
|
|
|
|
|

О П А
|
|
|
|
|
. |
|
а ал ні рівн нн |
удівел но |
|
е аніки |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
іст |
|
лави |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
. |
тержневі систе |
|
и |
к систе |
и |
і скінченни |
число |
ступнів віл ності |
|
|
|
|
|||||||||||||||||||
|
4. |
. |
івн нн |
статики |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
. |
. |
ео |
етричні рівн нн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
. |
. |
і ичні рівн нн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
. |
. Постановка |
адач удівел но |
е аніки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
. |
. |
оловні властивості статично ви начувани |
і статично неви начувани |
|
систе |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1. тержневі системи як системи зі скінченним числом ступнів вільності |
|
|
|
||||||||||||||||||||||||||||||
|
Однією |
оловни |
|
арактеристик |
уд - |
ко систе |
и є кіл кіст |
ступнів віл ності, то то |
|||||||||||||||||||||||||
|
іні |
ал на |
кіл кіст |
|
не алежни |
ео |
етрични |
|
пара |
етрів, |
|
о |
ви начают |
положенн |
всі |
||||||||||||||||||
еле |
ентів систе и. |
|
исло ци |
пара |
етрів, |
ке при виконанні кіне |
атично о аналі у ви началос |
|
а |
||||||||||||||||||||||||
фор |
улою |
е ишова, становило скінченну величину. |
е |
уло пов |
|
ано |
ти |
, |
о всі систе |
|
и |
||||||||||||||||||||||
ро |
л далис |
к такі, |
о складают с |
окре |
и |
дисків, то то |
жорстки |
еле |
ентів, |
дефор |
аці |
||||||||||||||||||||||
|
ки |
а о в а алі відсутні, |
а о настіл ки |
алі, |
о ни и |
ожна не тувати. л |
аналі у таки |
систе |
|||||||||||||||||||||||||
нео |
ідно використовувати скінчену кіл кіст |
ал е ра чни |
рівн н |
рівнова и. |
асправді ж |
уд - |
|||||||||||||||||||||||||||
|
ка дефор |
івна систе |
а |
|
ає нескінченну кіл кіст |
ступнів віл ності. |
ак, дл |
авданн на пло |
ині |
||||||||||||||||||||||||
положенн |
точок дефор |
овано осі |
алки потрі но нати пере |
і |
енн |
кожно |
точки. Оскіл ки |
||||||||||||||||||||||||||
число таки |
точок є нескінченно велики , |
то й кіл кіст |
пара |
етрів, |
|
о ви начают |
дефор овану |
||||||||||||||||||||||||||
віс |
алки, |
також |
уде нескінченни . |
івнова а систе |
нескінченно великою кіл кістю ступнів |
||||||||||||||||||||||||||||
віл ності |
ате |
атично описуєт с диференціал ни и а о інши |
и функціонал ни |
и рівн нн |
|
и. |
|||||||||||||||||||||||||||
|
о в |
анн |
таки |
рівн н |
часто становит |
чи алі складно |
і. Проте |
ожна пока ати, |
о в ра і |
||||||||||||||||||||||||
відсутності |
ро поділено о |
в довж |
стержн |
навантаженн |
положенн |
уд - |
ко |
точки |
|||||||||||||||||||||||||
дефор |
овано осі цілко |
ви начаєт с пере |
і |
енн |
|
и йо о кінців [10]. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
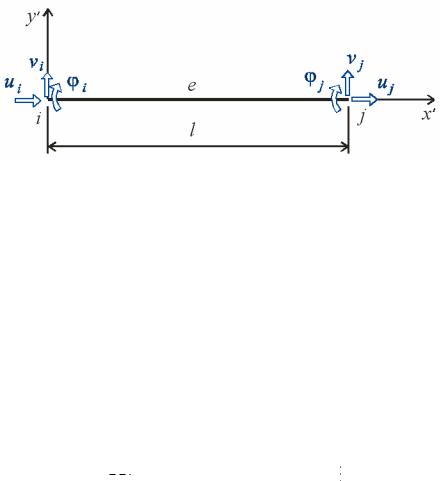
4. |
ага |
ні рівн нн |
іве |
но |
ме ані и |
|
|
2 |
|
правді, |
ро |
л не о віл ний від ро поділени овнішні навантажен стержен |
e рис. |
. |
, |
||||
кінец |
ко о i |
ає поступал ні |
пере |
і енн |
ui ,vi і поворот i , а протилежний |
кінец |
j |
|
|
пере |
і енн |
u j ,v j і поворот j . |
|
|
|
|
|
||
ис.4.1
укупності ци пере і ен ожут ути аписані у ви л ді атриц -стовпців векторів
|
|
|
|
|
δi |
|
ui |
|
|
δj |
u j |
|
|
|
|||
|
|
|
|
|
|
vi |
; |
|
v j . |
|
|
||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
|
Пере і |
енн о о |
кінців стержн також |
ожна |
аписати у ви л ді вектора |
|
||||||||||||
|
|
|
|
|
ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δi |
|
|
vi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
T |
|
|
ui vi |
i u j |
T |
|
||||
|
δe |
|
|
|
u j |
δi |
δ j |
e |
|
|
v j j e . |
(4.1) |
|||||
|
|
δ j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
v j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
По удує |
о фор улу дл |
|
ви наченн |
пере |
і |
ен |
у |
уд - |
кій точці стержн чере |
пере і енн |
|||||||
йо о кінців. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иференціал не рівн нн |
по довжні |
дефор |
|
ацій і диференціал не рівн нн |
ину стержн в |
||||||||||||
ра і відсутності ро поділени |
навантажен |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
d 2u |
|
0, |
|
|
|
d 4v |
|
0 |
|
|
(4.2) |
|
|
|
|
|
|
dx2 |
|
|
|
dx4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ают ро в |
ки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
1 |
2 x , |
|
|
|
|
|
(4.3) |
||||
|
|
|
|
v 3 |
4 x |
|
5 x2 |
6 x3 . |
|
(4.4) |
|||||||

4. |
ага |
ні рівн нн |
іве |
но |
ме ані и |
|
|
|
|
3 |
||||||
|
ро в |
ку . |
ожна ви начити кут повороту в |
уд - |
ко у перері і стержн |
|
||||||||||
|
|
|
|
|
|
|
dv |
4 |
2 5 x |
3 6 x2 . |
|
|
(4.5) |
|||
|
|
|
|
|
|
dx |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
апише |
о вира и |
. |
, . |
в |
атричній фор |
і |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
δ( x ) |
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
u( x ) |
|
|
1 x |
0 |
0 |
0 |
0 |
3 |
L( x ) . |
(4.6) |
||||
|
|
|
e |
v( x ) |
e |
0 0 1 x x2 x3 |
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
Вира и о вектор коефіцієнтів |
чере |
пере |
і енн |
|
кінців |
стержн . к |
о підставити в |
|||||||||
(4.3) |
. координати початку |
xi |
= 0 |
і кінц |
xj |
=l , |
ати |
е |
о |
|
|
|
||||
|
|
|
|
ui |
1 , |
ul |
|
1 |
2l, |
|
|
|
|
|
||
|
|
|
|
vi |
3 , |
v j |
|
3 |
4l |
|
5l 2 |
|
6l3 , |
(4.7) |
||
|
|
|
|
i |
4 , |
l |
|
4 |
2 5l |
3 6l 2 . |
|
|||||
|
атричній фор |
і алежності . |
ожут |
|
ути |
аписані у ви л ді |
|
|||||||||
|
ui |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
vi |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
|
i |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
δe |
u j |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
||||||||
|
v j |
|
0 |
0 |
1 |
l |
l 2 |
l3 |
|
|
|
j |
e |
0 |
0 |
0 |
1 |
2l |
3l 2 |
|
|
|
|
|
|
|
|
||
одержано рівності ви начає |
о вектор коефіцієнтів |
: |
|||||||
Le1δe .
ц о у співвідношенні о ернена атриц Le1 ає ви л д
1 |
|
|
|
|
2 |
|
|
|
|
3 |
Le |
|
. |
(4.8) |
4 |
|
|||
|
|
|
|
56
(4.9)
4. ага ні рівн нн іве но ме ані и 4
|
|
|
|
|
|
1 |
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 l |
|
|
0 |
|
0 |
|
1 l |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Le1 |
|
0 |
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
0 |
. |
|
|
|
|
|
|
(4.10) |
|||
|
|
|
|
|
0 |
|
|
0 |
|
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
3 l 2 |
|
2 l |
0 3 l 2 |
|
1 l |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
2 l3 |
1 l 2 |
0 |
|
|
2 l3 1 l 2 |
|
|
|
|
|
|
|
|
|
|||||||
Підставл ючи . |
до |
. , |
|
ати |
е |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
(x)e |
L(x)Le1 e . |
|
|
|
|
|
|
|
|
|
|
(4.11) |
|||||||
о уток |
атриц |
L(x) L -1 |
в . |
|
також є |
атрицею, еле |
енти |
ко |
|
вл ют |
со ою функці |
||||||||||||||||||
координати x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
1 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L(x)Le |
0 |
|
1 3 |
2 |
2 |
3 |
x(1 |
2 |
|
2 |
) 0 |
3 |
2 |
2 |
3 |
x( |
|
2 |
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
) |
|
||||||||||||||||||
де = x/l відносна координата точки на осі стержн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Еле |
енти одержано |
атриці |
|
це функці , |
|
кі виражают |
пере |
і |
енн |
точки |
відносною |
||||||||||||||||||
координатою |
в довж осі x |
|
перший р док |
|
атриці і в довж осі y стержн |
дру ий р док |
|||||||||||||||||||||||
атриці |
від одинични |
пере |
і ен |
йо о кінців. Перший стовпец |
|
від пере |
і |
енн |
ui |
= 1, |
|||||||||||||||||||
дру ий |
від vi = 1 то |
о. |
а начені функці на ивают с |
|
функціями форми. Вира |
. |
|
дає |
о у |
||||||||||||||||||||
ви начити пере |
і енн |
уд - |
ко |
точки стержн |
к |
|
о пере |
і |
енн |
йо о кінців відо |
і. |
о у |
|||||||||||||||||
ожна ка ати, |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Ви начи |
о, |
наприклад, пере |
і |
енн |
в |
середині |
|
про ону |
стержн , |
лівий |
кінец |
ко о |
|||||||||||||||||
повертаєт с |
на кут , а правий |
|
пере |
і уєт с |
|
ввер |
на величину f. накше кажучи, |
ає |
|
о |
|
||||||||||||||||||
|
|
|
|
|
ui = 0, |
|
|
vi = 0, |
|
|
i = , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
uj = 0, |
|
|
vj = f, |
|
|
j = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Відносна координата перері у, о нас цікавит , = 0, . О числи о пере і енн а фор улою
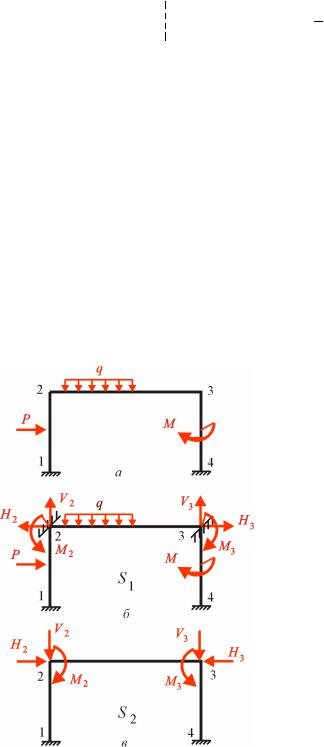
4. |
ага ні рівн нн |
|
іве |
но |
ме ані и |
|
|
|
|
|
|
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
u(x) |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0.5 |
0 |
|
0 |
0.5 |
0 |
|
|
0 |
|
|
|
||||
|
|
|
(x)e |
v(x) e |
0 |
|
0.5 |
0.125l |
0 |
0.5 |
|
0.125l |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.125l |
0.5 f . |
|
|
|
|
|
|
|
|
|
|
|
|
|
е ай на плоску ра у |
рис. . |
,а , |
ка складаєт с |
|
тр о |
еле |
ентів, |
о поєднуют с |
іж |
|||||||||
со ою у ву ла |
і |
, діє довіл не овнішнє навантаженн . |
|
|
|
|
|
|
|
||||||||||
|
апружено-дефор |
ований |
стан ра и |
оже |
ути |
представлений |
к су а |
напружено- |
|||||||||||
дефор овани |
станів |
дво |
систе |
S1 |
i |
S2. |
исте |
а S1 рис. |
. |
, |
утворена і |
адано ра |
и |
||||||
акріпленн |
всі |
|
ву лів |
від |
уд - |
ки |
ожливи |
пере і |
ен , а систе а S2 |
рис. . ,в |
|
||||||||
пере уває під дією тіл ки ву лови |
навантажен , |
кі дорівнюют |
а величиною і протилежні |
а |
|||||||||||||||
напр |
а и реакці |
в |
ей, |
|
о введені до систе |
и S1. |
|
|
|
|
|
|
|
|
|||||
|
|
ис.4.2 |
|
|
еруючис принципо суперпо иці ро ра унок ви ідно |
ра и ожна ро класти на два етапи |
|
1) |
ро ра |
унок окре и стержнів к однопро онови алок на дію ро поділени навантажен |
|
2) |
ро ра |
унок всіє стержнево систе и на дію лише ву лови |
навантажен . |
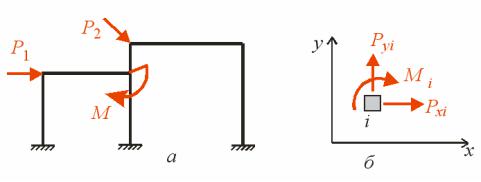
4. ага |
ні рівн нн |
|
іве |
но |
ме ані и |
|
|
|
6 |
|||
Перший етап ро ра унку виконуєт с |
а |
етода |
и опору |
атеріалів. При ц о |
у ви начают с |
|||||||
реакці у вни |
опор в окре и |
стержн |
і напружений стан стержнів від ді ро поділено о на |
|||||||||
стержн |
навантаженн . |
ру ий етап є най іл ш трудо істки і оже ро |
л датис |
к основна |
||||||||
адача ро ра унку стержнево |
систе |
и. |
а дано |
у етапі ра |
а ро ра овуєт с |
тіл ки |
одо ді |
|||||
ву лови |
навантажен . |
адача ц , |
к |
така, |
о ає скінченне число |
ступнів |
віл ності, |
|||||
описувати |
ет с |
скінченною систе ою ал е ра чни |
рівн н . |
|
|
|
|
|||||
4.2. |
івняння статики |
|
|
|
|
о |
л не о стержневу систе у, |
ка складаєт с |
пр |
олінійни |
стержнів постійно жорсткості |
і авантажена у ву ла осереджени |
и сила и та |
о ента |
и рис. |
. ,а . |
|
|
|
|
|
|
ис.4.3 |
|
|
|
|
|
|
|
л |
довіл но о ву ла рис. |
. , |
сукупніст |
овнішні |
навантажен |
оже |
ути представлена у |
|||||
ви л ді |
атриці-стовпц , то то вектора |
|
|
|
|
|
|
|
||||
|
|
|
|
Pxi |
а о |
T |
Pxi |
Pyi |
Mi |
, |
|
(4.12) |
|
|
Fi |
Pyi |
Fi |
|
|||||||
|
|
|
|
Mi |
|
|
|
|
|
|
|
|
причо |
у де кі ко |
поненти |
ожут |
дорівнювати нулю. Ву лові навантаженн |
дл всіє |
систе и, |
||||||
о ає m ву лів, також пода |
о у ви л ді вектора |
|
|
|
|
|
|
|
||||
|
FT |
F1 F2 |
Fn |
={Px1 Py1 |
M1 |Px2 Py2 M2| |
...| Pxm Pym |
Mm }. |
(4.13) |
||||
к відо о, рівн нн рівнова и стержнево систе и ают ви л д див.п. .
|
AS |
F , |
(4.14) |
де |
– атриц рівнова и стержнів і ву лів, |
S, F вектори внутрішні |
усил і овнішні |
навантажен . |
|
|
|

4. ага |
ні рівн нн |
іве |
но |
ме ані и |
|
7 |
|||
Вектор |
внутрішні усил |
у |
систе |
і, |
о |
складаєт с |
n стержнів, |
ожна представити у |
|
ви л ді |
|
|
|
|
|
|
|
|
|
|
|
ST |
s1 |
s2 |
se |
sn . |
(4.15) |
||
ц о |
у співвідношенні se |
вектор кінцеви |
усил |
у стержні рис. . |
|
||||
ис.4.4
|
|
|
|
seT |
Mi |
Qi |
Ni |
M j |
Qj |
N j . |
|
|
|
|
|
(4.16) |
|||
ра і відсутності ро поділени |
в довж стержн |
навантажен кіл кіст |
|
не алежни |
пара |
етрів, |
|||||||||||||
о ви начают |
напружений |
стан |
стержн , |
|
ожна скоротити. |
асправді, |
складе |
о рівн нн |
|||||||||||
рівнова и дл стержн |
рис. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Fx |
0 |
|
Ni |
N j |
0 Ni = N j |
N; |
|
|
|
|
|
||||||
|
|
Fy |
0 |
|
Qi |
Q j |
|
0 |
Qi = Q j = Q; |
|
|
|
|
|
|
(4.17) |
|||
|
|
M i |
0 |
M i |
M j |
Q jl 0 Q M j |
Mi |
l. |
|
|
|||||||||
ци співвідношен |
випливає, |
о всі шіст |
ко |
понентів кінцеви |
усил . |
ожут |
ути |
||||||||||||
виражені чере |
три пара |
етри |
N, Mi, Mj. |
атрично у ви л ді |
ає |
о |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 l |
1 l |
|
0 |
Mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sek |
|
|
M j |
|
de se . |
|
|
|
|
|
(4.18) |
||||
|
|
|
|
|
0 |
1 |
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 l |
1 l |
|
0 |
e |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
апропонована процедура |
еншує |
а ал ну кіл кіст |
невідо и |
пара |
етрів, кі ви начают |
||||||||||||||
напружений стан систе |
и. |
ак, к |
о систе |
а складаєт с |
n стержнів, |
то кіл кіст |
не алежни |
||||||||||||
пара етрів складати |
е |
n. |
к |
о ж систе а |
істит |
m ву лів, |
то кіл кіст |
рівн н рівнова и, кі |
|||||||||||
ожна скласти, становити |
е |
m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

4. |
ага |
ні рівн нн |
|
іве |
но |
ме ані и |
|
|
|
|
|
|
|
|
|
|
8 |
||||||||||
4.3. |
еометричні рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Внаслідок |
|
виникненн |
|
внутрішні |
усил |
|
стержні |
дефор |
уют с , |
ву ли |
систе и |
||||||||||||||||
пере |
і |
уют с , |
|
і |
ви л д |
споруди |
інюєт с . |
Проте стержні |
не відокре люют с |
один |
від |
||||||||||||||||
одно о. Вони дефор уют с |
су |
існо |
і у |
оджено, |
алежно |
від |
пере і |
ен |
|
ні |
кінців, |
о |
|||||||||||||||
вл ют |
со ою |
ву ли стержнево |
систе |
и. |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
О начені |
|
алежності |
ожна представити в |
атричній фор і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(4.19) |
|
де |
|
вектор пере і ен |
ву лів систе |
и, G – де ка, поки |
о неви начена, |
атриц . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
m . |
|
|
|
|
|
|
|
(4.20) |
|||
ожен ву ол i |
ає три ко поненти пере |
і |
ен |
|
xi, |
yi |
поступал ні пере |
і |
енн |
в напр |
ка |
||||||||||||||||
осей x i y, а також кут повороту i |
ву ла. Отже, |
дл |
уд - |
ко о ву ла |
|
оже |
о |
аписати вектор |
|||||||||||||||||||
пере |
і |
ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
i |
. |
|
|
|
|
|
|
|
|
(4.21) |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
xi |
|
yi |
|
|
|
|
|
|
|
|
||||
Вектор пере |
|
і |
ен всіє |
систе |
и |
оже |
ути аписаний у ви л ді |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
1 |
2 |
|
m |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
x1 |
y1 |
1 |
|
x2 |
|
y2 |
|
2 |
|
xm |
|
ym |
m |
. |
|
|
(4.22) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вектор |
e |
арактери ує дефор аці |
стержнів. |
|
кожно |
у стержні дефор |
аці , |
кі ви начают |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор se , |
ожут |
ути представлені у ви л ді вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
i |
|
j |
l |
. |
|
|
|
|
|
|
|
|
(4.23) |
|||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
||||||||
Отже, повний вектор дефор |
ацій усіє стержнево систе |
и |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
T |
1 |
|
2 |
n |
|
|
|
|
|
|
|
|
|
(4.24) |
||||
оже |
ути |
аписаний у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
T |
|
|
i1 |
j1 |
|
l1 |
|
i2 |
j2 |
|
l2 |
in |
|
jn |
|
ln . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4. |
ага |
ні рівн нн |
|
|
іве |
но |
|
ме ані и |
|
|
|
|
|
|
|
|
|
9 |
|||||||
л |
ви наченн |
атриці |
G |
|
ео |
етрични |
рівн н |
|
скористає |
ос |
принципо |
ожливи |
|
||||||||||||
пере |
і |
ен , |
ідно |
ки |
су |
а ро іт всі |
|
овнішні |
і внутрішні |
сил на |
уд - |
ки |
ожливи |
|
|||||||||||
нескінченно |
али |
пере і |
енн |
дорівнює нулю |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
U |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
а |
ожливі ві |
|
е о дійсні пере |
і |
енн |
систе |
и, |
кі ви начают с |
векторо |
. |
|
|
|||||||||||||
овнішні сили, |
|
о прикладені до ву лів, дійснюют |
ро оту на пере |
і енн |
ву лів |
|
|||||||||||||||||||
|
|
|
|
|
A=Px1 x1+ Py1 |
y1+M1 1+ Px2 |
x2+ Py2 |
y2+M2 2...+ |
|
|
|
|
|||||||||||||
|
|
|
|
|
+ Pxm xm+ Pym ym+Mm m = FT . |
|
|
|
|
|
|
|
|
||||||||||||
Внутрішні сили |
дійснюют |
ро оту на дефор |
аці |
стержнів |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
U= |
Mi1 |
i1 |
Mj1 j1 N1 |
l1 |
Mi2 |
i2 |
Mj2 j2 |
N2 |
l2 ... |
|
|
|
||||||||||
|
|
|
|
|
Min in |
Mjn jn Nn |
ln = ST . |
|
|
|
|
|
|
|
|
|
|
||||||||
нак |
інус |
поставлено |
то |
у, |
о |
усилл |
Nk, |
Mik, Mjk |
по відношенню до еле ента є |
||||||||||||||||
овнішні и. Внутрішні сили, |
кі перешкоджают |
дефор |
аці |
, дорівнюют |
ци |
усилл |
а |
||||||||||||||||||
наченн |
, але діют |
у протилежно |
у напр |
|
і. Отже, повна ро ота |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
FT |
|
ST |
0 . |
|
|
|
|
|
|
|
|
|
|
||
Підставл ючи в одержану рівніст |
вира и дл |
векторів навантаженн . |
|
і дефор |
ацій . |
, |
|||||||||||||||||||
ати |
е |
о |
|
|
|
|
|
|
|
AS |
|
|
T |
|
0. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|||||||
|
ре ул таті виконанн |
операці |
транспонуванн |
до утку дістане |
о |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ST AT |
|
T |
|
|
. |
|
|
|
|
|
|
|
|
||
Порівнюючи ліву і правучастини рівності |
ачи |
о, |
о: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
G |
|
AT , |
|
|
|
|
|
|
|
|
|
(4.25) |
||
то то матриця геометричних рівнянь дорівнює транспонованій матриці рівнянь рівноваги.
Одержаний вира вл є со ою так |
вану статико-геометричну аналогію. |
|
Отже, ео етричне рівн нн . |
оже ути переписане у ви л ді |
|
|
AT . |
(4.26) |
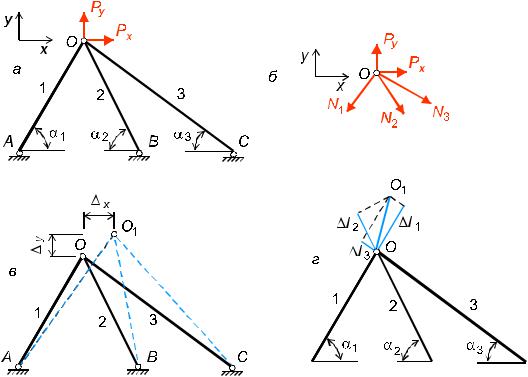
4. ага |
ні рівн нн |
|
іве |
но |
ме ані и |
|
10 |
|||
л |
ілюстраці |
статико- |
ео |
етрично анало і |
ро л не |
о фер у, ка |
ає тіл ки один ву ол |
|||
рис. . |
,а і |
авантажена дво |
а сила |
и Px |
i Py. |
Виокре |
люючи ву ол |
рис. . , і складаючи |
||
рівн нн |
рівнова и |
ати е |
о |
|
|
|
|
|
|
|
Fx = 0 |
|
N1cos 1 |
+ N2cos 2 + N3cos 3 + Px = 0, |
|
|
|||||
|
|
|
N1cos 1 |
N2cos 2 |
N3cos 3 = Px; |
|
|
|||
Fy = 0 |
|
N1sin 1 |
N2sin 2 |
N3sin 3 + Py = 0, |
|
|
||||
N1sin 1 +N2sin 2 + N3sin 3 = Py.
ис.4.5
По начи о |
1 = a11, |
cos 2 = a12, |
cos 3 = a13; |
sin 1 = a21, |
sin 2 = a22,, sin 3 = a23. |
оді ожна |
аписати, |
о |
|
|
|
|
|
a11 |
|
a12 |
a13 |
N1 |
Px . |
|
|
||
|
|
|
N |
2 |
|
|
|||||
|
|
a21 |
|
a22 |
a23 |
|
Py |
|
|
||
|
|
|
N3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
Отже в дано у випадку ST |
N1 |
|
N2 |
N3 , FT |
|
Px Py |
, атриц рівн н рівнова и |
||||
A= |
a11 |
a12 |
a13 = |
cos 1 |
|
cos 2 |
cos 3 . |
||||
|
a |
a |
a |
23 |
sin |
|
|
sin |
2 |
sin |
3 |
|
21 |
22 |
|
1 |
|
|
|
|
|||
4. |
ага |
ні рівн нн |
|
іве |
|
но |
ме ані и |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|||||||||||
|
Встанови |
о надалі аналітичну |
алежніст |
|
іж дефор аці |
и стержнів і пере і енн |
и ву ла |
||||||||||||||||||||||||
|
фер и. Вважати е о, |
о всі стержні видовжуют с |
і ву ол |
пере |
і |
уєт с |
в положенн |
|
1 |
||||||||||||||||||||||
|
рис. . ,в . Вира и |
о видовженн |
стержнів |
l1, |
l2, |
l3 чере |
пере |
і |
енн |
ву ла |
x i |
y. |
|
|
|
||||||||||||||||
|
Беручи до ува и, |
о видовженн |
стержнів |
алі порівн но |
|
ні и первісни и довжина и, |
|||||||||||||||||||||||||
|
нове положенн |
ву ла |
1 |
ожна відшукати наступни |
чино |
. Відкладе |
о видовженн |
уд - |
ки |
||||||||||||||||||||||
|
дво |
стержнів, |
наприклад |
першо о |
і трет о о, в |
напр |
а |
|
ні |
осей і |
|
кінців |
постави |
о |
|||||||||||||||||
|
перпендикул ри. О начені перпендикул ри |
а |
інюют |
ду и, |
а |
ки |
и повертают с |
видовжені |
|||||||||||||||||||||||
|
стержні |
і |
довкола точок |
прикріпленн . |
аки |
чино |
на оди |
о положенн |
видовжени |
||||||||||||||||||||||
|
першо о і трет о о стержнів. |
Оскіл ки післ |
дефор |
аці систе |
а |
алишаєт с |
цілісною, в точці |
1 |
|||||||||||||||||||||||
|
повинен |
на одитис і кінец |
стержн . |
|
л |
|
ви наченн |
відповідно о видовженн |
|
і повороту |
|||||||||||||||||||||
|
ц о о стержн |
постави о перпендикул р і |
точки |
1 |
на напр |
стержн |
, |
авд ки чо |
у |
уде |
|||||||||||||||||||||
|
одержано |
видовженн |
l2 |
рис. |
. , |
. |
ові |
координати точки |
|
вл ют |
со ою |
поступал ні |
|||||||||||||||||||
|
пере і енн ву ла |
x i |
y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Отже |
ає |
о дл |
першо о стержн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
l1 = |
xcos 1 + |
|
ysin 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
дл |
дру о о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 = |
|
xcos 2 + |
ysin 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
дл |
трет о о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 = |
|
xcos 3 + |
ysin 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Перепише |
о одержані рівності в |
атричній фор |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
l1 |
|
cos 1 |
|
sin 1 |
|
x |
|
a11 |
a21 |
|
x . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
l |
|
cos |
2 |
sin |
2 |
|
|
a |
|
a |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
y |
|
12 |
22 |
|
y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
l3 |
|
cos 3 |
sin 3 |
|
|
a13 |
a23 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
По начивши T ={ |
l1 |
|
l2 |
l2}, |
|
T = { x |
|
y}, по ачи |
о, |
о |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Отже, |
к і |
уло доведено, |
атриц |
|
ео |
етрични |
рівн н |
G дорівнює транспонованій |
атриці |
|||||||||||||||||||||
|
AT |
рівн н рівнова и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
івн нн |
рівнова и . |
і |
ео |
етричні |
рівн нн |
. |
|
не |
пов |
ані |
|
фі ични |
и |
||||||||||||||||
|
арактеристика |
и |
конструкці . |
о |
у |
вони |
однаковою |
ірою |
ожут |
ути |
використані |
дл |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
ага |
ні рівн нн |
|
іве |
но |
ме ані и |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ро ра унку конструкцій |
к і |
пружни , так і |
|
пластични |
|
атеріалів. стержневи систе |
а ці |
|||||||||||||||||||||||
|
рівн нн |
є лінійни и |
ал е ра чни |
и. |
інійніст |
о у |
овлена |
припу |
енн |
|
|
одо |
али ни |
||||||||||||||||||
|
дефор |
ацій, внаслідок чо о рівн нн |
рівнова и складают с |
дл |
недефор |
овано с е |
и споруди. |
||||||||||||||||||||||||
|
исте |
и, |
дл |
|
ки |
|
оже |
ути |
покладени |
таке |
припу |
енн , |
на ивают с |
|
геометрично |
||||||||||||||||
|
лінійними. |
к |
о ж пере |
і |
енн |
не є |
али и, рівн нн |
статики складают с |
дл |
дефор овано |
|||||||||||||||||||||
|
с е и, то то |
|
ура уванн |
|
пере і |
ен . Оскіл ки пере і |
|
енн , в свою чер у, |
алежат |
від |
|||||||||||||||||||||
|
усил , |
рівн нн |
рівнова и |
удут |
нелінійни |
и. |
о |
у такі систе |
и на ивают |
геометрично |
|||||||||||||||||||||
|
нелінійними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
оча статичні та |
ео |
|
етричні рівн нн |
складені не алежно одне від одно о, |
іж ни |
и існуют |
||||||||||||||||||||||||
|
певні |
в |
|
ки. |
Передовсі |
, |
використовуючи |
атрицю рівн н |
|
одніє |
кате орі , |
|
ожна фор |
ал но |
|||||||||||||||||
|
аписати |
рівн нн |
іншо |
|
кате орі . |
е |
на а ато поле шує |
складанн |
ео |
етрични |
рівн н , |
||||||||||||||||||||
|
оскіл ки |
ео |
етричне |
дослідженн |
споруд |
становит |
чи |
алі |
трудно |
і, |
а |
складанн |
рівн н |
||||||||||||||||||
|
рівнова и |
дійснюєт с |
порівн но просто. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
снує |
також певний |
|
в |
|
ок |
іж |
вектора |
и навантажен |
F і |
пере |
і |
ен |
|
. |
|
асправді, |
||||||||||||||
|
кіл кіст |
ко понентів кожно о вектора у ву лі і, таки |
|
чино |
, у всій систе і однакове. Анало ічна |
||||||||||||||||||||||||||
|
алежніст |
існує |
іж вектора и |
усил |
S і дефор |
ацій . |
|
о у, |
к |
о певний р док рівн н |
|||||||||||||||||||||
|
рівнова и |
вл є со ою су |
у проекцій всі |
овнішні |
|
і внутрішні |
сил на |
ку-не уд |
|
віс , то в |
|||||||||||||||||||||
|
ео етрични |
рівн нн |
|
ко понента вектора пере |
і |
ен |
дорівнювати |
е пере |
і |
енню ву ла в |
|||||||||||||||||||||
|
напр |
і ціє осі. |
к |
о |
усилл |
S в одит |
до рівн нн |
статики в стовпец |
i |
атриці A, |
то в р дку |
||||||||||||||||||||
|
ео етрични |
рівн н |
ати |
е |
о ко поненту дефор аці i, |
о відповідає |
усиллю Si. |
|
|
|
|||||||||||||||||||||
|
аведені два висновки |
ожут |
ути у а ал нені таки |
правилом подвійності |
у |
ова |
одніє |
||||||||||||||||||||||||
|
систе |
и відповідают |
інні іншо |
систе |
и і навпаки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4.4. Фізичні рівняння
|
|
|
|
. |
о |
л не |
о |
окре |
ий |
стержен |
i-j, |
|
навантажений кінцеви |
и по довжні |
и сила |
и N і инаючи |
и о |
ента |
и Mi |
i Mj |
рис. . ,а . |
||||
По довжн дефор |
аці |
стержн виражаєт с чере по довжню силу |
а аконо |
ука |
|
|||||||
|
|
|
l N |
l |
. |
|
|
|
|
|
|
(4.27) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
EA |
|
|
|
|
|
|
|
|
ути повороту на кінц |
стержн |
на підставі принципу не алежності ді сил виражают с |
чере |
|||||||||
кінцеві о енти алежност |
и |
|
|
|
|
|
|
|
|
|
|
|
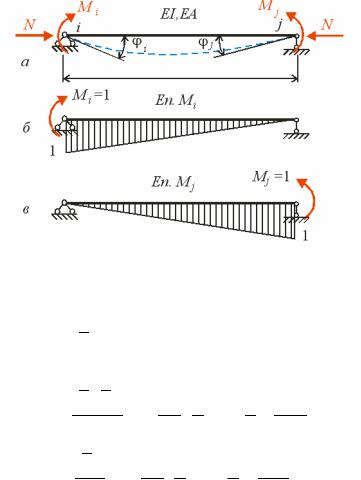
ні рівн нн |
іве |
но ме ані и |
|
13 |
|
|
i |
ii M i |
ij M j |
, |
(4.28) |
|
j |
ji M i |
jj M j . |
||
|
|
||||
ii
ij
jj
l |
M 2 |
dx |
1 |
1 |
1 |
l |
2 |
|
l |
, |
|
|
|
i |
|
|
|
|
|
|
|||||
0 |
EI |
|
|
EI |
2 |
|
|
3 |
|
3EI |
|
|
l MiM j |
dx |
1 |
1 |
1 |
l |
1 |
|
l |
, |
|||
|
EI |
EI |
2 |
3 |
6EI |
|||||||
0 |
|
|
|
|
||||||||
l |
M 2j |
dx |
1 |
1 |
1 |
l |
2 |
|
l |
. |
|
|
|
EI |
|
EI |
2 |
3 |
|
3EI |
|
||||
0 |
|
|
|
|
|
|
|
|||||
алежності . |
. |
у атричній фор і |
ати ут |
ви л д |
|
|
|
|
|
|
e |
bese . |
|
|
(4.29) |
T |
={ i |
i |
|
|
T |
Mi M j |
N e |
ут по начено e |
l}e вектор дефор |
ацій стержн se |
|||||
вектор кінцеви усил |
be |
атриц |
податливості стержн e, ка ає ви л д |
|
|
||
4. ага ні рівн нн |
іве но ме ані и |
14 |
|
|
|
|
|
|
|
l |
l |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3EI |
6EI |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
be |
|
l |
l |
0 |
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
6EI |
3EI |
||||||
|
|
|
|
|
|
|
l |
|
|||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
EA e |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
л |
всіє систе |
и, о складаєт с |
n еле |
ентів, ає |
ісце |
алежніст |
|||||||
|
|
|
|
|
|
BS, |
|
|
|
|
|
||
де T |
1 |
2 |
n |
вектор дефор |
ацій всіє |
систе |
и, |
|
|||||
ST |
s1 |
s2 |
sn |
вектор |
усил всіє систе и, |
|
|
|
|||||
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
b2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
bn |
|
|
|
|
ква ідіа онал на |
атриц , |
о складена |
атриц податливості окре |
и стержнів. |
|||||||||
(4.30)
(4.31)
4.5. Постановка задач будівельної механіки
Повна систе а рівн н удівел но е аніки складаєт с тр о руп алежностей статичні співвідношенн .
A S F ;
|
ео етричні співвідношенн |
. |
|
|
|||
|
|
|
|
|
|
AT |
; |
|
фі ичні співвідношенн |
. |
|
|
|
||
|
|
|
|
|
|
BS. |
|
|
нфор ацію |
одо о |
єкта, |
кий ро ра овуєт с , |
ожна ро поділити на три типи |
||
1) |
ео етрична і тополо ічна інфор аці координати ву лів систе и і в ок по іж ву ла и |
||||||
2) |
фі ична інфор |
аці |
жорсткості поперечни |
перері ів EI i EA); |
|||
3) |
авантаженн |
систе |
и |
вектор овнішні навантажен F ). |
|||
При ц о у нео ідно ви начити
4. |
ага |
ні рівн нн |
іве |
но |
ме ані и |
|
15 |
||||
1) |
усилл |
у всі |
стержн |
|
вектор S ); |
|
|
|
|
||
2) пере і |
енн |
всі ву лів систе и вектор |
). |
|
|
|
|||||
|
Отже, відо и и є вектор F , а невідо и |
и |
вектори S і . л ро в анн адачі достатн о |
||||||||
по удувати дві |
атриці |
атрицю у ов рівнова и A і атрицю податливості B. |
|
||||||||
4.6. |
оловні властивості статично визначуваних і статично невизначуваних |
||||||||||
|
систем |
|
|
|
|
|
|
|
|
||
|
ра і, |
к |
о систе |
а, |
о ро ра овуєт с , |
становит |
статично ви начувану с е |
у, атриц |
|||
рівн н |
рівнова и A є квадратною і, |
отже, |
ає о ернену |
атрицю A–1. оді рівн нн |
рівнова и |
||||||
(4.14) ви начаєт с |
вектор S : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = A–1 F . |
|
|
|
|
|
|
|
|
|
|
(4.32) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
відси |
випливає, |
|
о |
дл |
о численн |
усил |
в |
статично |
ви начувани |
систе |
а |
не |
ає |
|||||||||||||||
нео |
ідності |
удувати і використовувати |
атрицю податливості. |
накше кажучи, |
усилл |
в |
|||||||||||||||||||||||
статично ви начувани |
|
систе |
а |
не |
алежат |
від жорсткостей |
ні |
еле ентів. |
л |
ро в |
анн |
||||||||||||||||||
адачі |
нео |
ідно |
лише, |
о и |
атриц |
рівн н |
|
рівнова и |
ула |
неосо ливою, то то |
о |
|
|||||||||||||||||
ви начник не дорівнював нулю й, отже, систе |
а ула |
|
иттєво не |
інюваною. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Виключаючи дефор |
|
аці |
|
ео |
етрични |
(4.26) і фі ични |
. |
рівн н , одержи |
о |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AT |
|
B S , |
|
|
|
|
|
|
|
|
|
(4.33) |
|||
відки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
T |
1 |
|
|
|
|
|
|
|
|
|
|
(4.34) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B S. |
|
|
|
|
|
|
|
|
||||
В окре |
о |
у випадку, коли |
овнішнє навантаженн |
відсутнє, то то вектор навантажен |
F |
0 , |
|||||||||||||||||||||||
. |
|
очевидно, |
о й вектор усил |
S |
|
0 . Отже, в ра і відсутності |
овнішн о о навантаженн |
||||||||||||||||||||||
усилл |
в статично ви начувани |
систе |
а |
не виникают . |
о |
у при ді |
тіл ки те |
пературно о |
|||||||||||||||||||||
пол |
а о |
при усово о |
|
і |
енн |
опор |
|
усилл |
в |
стержн |
|
статично |
ви начувани |
систе |
|||||||||||||||
дорівнюют |
нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При ро в |
анні статично неви начувани |
адач нео |
ідно, крі |
атриці рівнова и, |
ка не |
уде |
|||||||||||||||||||||||
квадратною |
|
див.п. . |
, |
по удувати також |
атрицю |
податливості, |
дл |
чо о |
нео |
|
ідно |
нати |
|||||||||||||||||
жорскісні |
арактеристики еле |
ентів систе |
и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
а |
цій підставі |
ожна |
ро ити |
ни ку |
висновків |
одо |
де ки |
властивостей |
статично |
|||||||||||||||||||
неви начувани систе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
о поділ |
усил |
в статично неви начувани |
систе |
а |
алежит від жорсткостей |
|
еле |
ентів. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
ага |
ні рівн нн |
іве |
но |
ме ані и |
|
|
|
|
|
16 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
о у |
при |
ро в |
анні таки |
адач нео |
ідно спочатку |
|
ки ос |
|
іркуван |
адатис |
|||||
|
|
жорсткост |
и еле |
ентів а о |
співвідношенн |
и. |
|
|
|
|
|
|
|||||
|
2. |
В статично неви начувани |
систе |
а , |
о |
на од т с під дією те |
пературно о пол а о |
||||||||||
|
|
при усово о пере |
і енн |
опор, |
усилл |
виникают |
навіт |
у |
ра і |
відсутності |
овнішні |
||||||
|
|
навантажен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. |
уйнуванн |
а о вилученн |
одніє |
а о |
декіл ко |
айви |
в |
ей не |
викликає |
не айно о |
||||||
|
|
руйнуванн |
всіє |
споруди. |
При |
ц о у |
|
інюєт с |
кіл кіст |
стовпців |
m атриці рівн н |
||||||
|
|
рівнова и A і отже вектори |
усил |
|
S і пере |
і |
ен |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

О П А
5. Енергетичні теореми і варіаційні принципи будівельної механіки
Зміст глави
. |
.Енер і |
дефор аці лінійно-пружно систе |
и |
|
|
|
|
|
|
|
|
||||||||||||||||
. |
. Повна потенціал на енер і |
дефор івно систе |
и |
|
|
|
|
||||||||||||||||||||
. |
. |
ункціонал і варіаці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
. |
. |
ео |
ідна у |
ова екстре |
у |
у функціоналу |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
. |
. Варіаційна постановка |
адачі про плоский |
|
ин |
|
|
|
|
|
|
|
|
|||||||||||||||
|
. |
. |
Основні співвідношенн |
адачі про плоский |
|
ин пр |
олінійно о стержн |
||||||||||||||||||||
|
. |
. |
ор |
ула ріна дл |
адачі про плоский |
|
ин |
|
|
|
|
|
|
|
|||||||||||||
. |
. Варіаційне рівн нн |
|
а ранжа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
. |
. Варіаційне рівн нн |
|
астіл |
но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
. |
. Екстре |
ал ні властивості функціоналів |
а ранжа і астіл |
|
но |
||||||||||||||||||||||
. |
. Пр |
і |
етоди ро в |
анн варіаційно |
адачі |
|
|
|
|
|
|
|
|||||||||||||||
|
. |
. |
. |
етод |
ітца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
. |
. |
етод Бу нова- |
|
ал оркіна |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
. |
. |
. |
етод |
реффца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. |
. |
|
етод скінченни еле |
ентів к пр |
ий варіаційний |
етод |
|
||||||||||||||||||||
|
. |
. |
. |
етод скінченни |
еле |
ентів у фор |
і |
|
етоду пере |
і |
ен |
||||||||||||||||
|
. |
. |
. |
етод скінченни |
еле |
ентів у фор |
і |
|
етоду сил |
|
|
|
|
|
|||||||||||||
апружено-дефор ований стан уд - |
ко систе и |
оже |
ути ви начений |
|
а допо |
о ою дво |
||||
еквівалентни |
під одів |
локал но о |
та |
інте рал но о. |
окал ний |
під ід |
а уєт с |
на повній |
||
систе і рівн н |
удівел |
но е аніки |
рівн нн статики |
. |
, ео |
етричні |
. |
і фі ичні . |
||

5. Енергетичні теореми і варіаційні принципи |
|
2 |
|||
рівн нн |
. нте рал ний під ід рунтуєт с |
на варіаційно |
у численні. Основни |
и пон тт и тут є |
|
енер і |
дефор аці систе и, ро ота овнішні і внутрішні |
сил і т.ін. О начений під ід спираєт с |
|||
на екстре ал ні принципи, ви од чи ки |
ожна вивчати і |
а ал ни по ицій |
к адачі статики, |
||
так і адачі дина іки і стійкості, а відтак такі принципи ожут |
вважатис універсал ни и. |
||||
5.1.Енергія деформації лінійно-пружної системи
процесі дефор уванн |
пружно систе |
и в |
еле |
ента |
накопичуєт с |
енер і , внаслідок чо о |
||||||
післ |
н тт |
овнішн о о |
навантаженн |
систе |
а повертаєт с |
до сво о |
первісно о ви л ду. |
|||||
О начена енер і на иваєт с |
потенціальною енергією деформації. Вона дорівнює дійсній ро оті |
|||||||||||
внутрішні сил (3.7) і вважаєт с |
додатною. В плоски |
стержневи |
систе |
а |
потенціал на енер і |
|||||||
дефор |
аці |
складаєт с |
енер і |
ро т ненн -стисненн , |
ину й |
суву і |
|
оже ути аписана у |
||||
ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
U1
2
l
N |
M |
Q dx . |
(5.1) |
0
Відносні дефор аці |
пов |
ані |
і |
усилл и |
а |
допо |
о ою |
фі ични співвідношен |
акон |
||||||||
ука |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
EA , |
|
|
M |
EI , |
|
Q |
GA |
|
(5.2) |
||||
а о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
, |
|
M , |
|
|
Q . |
|
(5.3) |
||||
|
|
|
|
|
EA |
|
|
|
EI |
|
|
GA |
|
|
|
||
Підставл ючи першу . |
а о дру у |
|
|
рупу |
. |
фі ични |
співвідношен у . одержує о |
||||||||||
вира дл |
потенціал но |
енер і дефор аці |
чере |
усилл |
|
|
|
|
|
|
|
||||||
|
|
U |
|
l |
N 2 |
|
dx |
l |
M 2 |
dx |
|
l Q2 |
dx |
(5.4) |
|||
|
|
|
0 |
2EA |
0 |
2EI |
|
0 |
2GA |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а о чере |
дефор аці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l EA 2 |
dx |
l |
EI 2 |
dx |
||
U |
2 |
|
2 |
|||
0 |
|
|
0 |
|
||
Потенціал ну енер ію дефор |
ацію |
ожна |
аписати й чере |
|||
до систе и прикладено n у а ал нени |
|
овнішні |
сил P1, P2, |
|||
суперпо иці усилл ожна аписати у ви л ді |
|
|
|
|||
l |
GA 2 |
dx. |
(5.5) |
|
2 |
||
0 |
|
|
овнішні навантаженн . ак, к о
, Pn , то на підставі принципу

5. Енергетичні теореми і варіаційні принципи |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
1P1 |
|
|
|
|
2 P2 |
|
|
|
n Pn ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
N |
N |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
1P1 |
|
|
|
|
2 P2 |
|
|
|
n Pn ; |
|
|
|
|
|
|
|
(5.6) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
M |
M |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1P1 Q2 P2 Qn Pn , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
де |
|
i , |
|
i , |
|
|
усилл |
від ді |
|
у а ал нено |
сили Pi |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
N |
M |
Qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
к о підставити |
алежності |
. |
|
|
|
до |
. |
|
|
|
, то післ |
|
перетворен дістане о |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
U |
|
1 |
|
11 |
P12 |
|
|
12 PP1 2 |
|
|
|
1n PP1 n |
|
|
21P2 P1 |
|
22 P22 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(5.7) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2n P2 Pn |
|
n1Pn P1 |
|
|
|
n2 Pn P2 |
|
|
nn Pn2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
оефіцієнти ij |
це еле |
енти |
|
|
|
атриці податливості.. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Виконає о |
адані перетворенн , |
|
коли |
|
енер і |
|
ви начаєт с |
|
тіл ки |
одни доданко |
, |
о |
||||||||||||||||||||||||||||||||||||||||||||||||||||
алежит від |
ину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
l |
M |
2 |
dx , |
|
|
|
|
|
|
|
|
|
(5.8) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2EI |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а навантаженн |
становл т лише дві сили P1 i |
P2 . оді ідно |
|
|
. |
инал ні |
о енти |
ожут |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ути аписані у ви л ді M |
|
|
|
1P1 |
|
|
2 P2 . Потенціал на енер і |
. |
в тако |
у ра і апишет с |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
M |
M |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
наступни |
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
l |
|
2 P2 |
|
|
|
2 |
|
1 |
|
2 P1P2 |
|
|
2 P2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
M |
M |
M |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
M |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
U |
|
|
|
|
|
|
|
1 1 |
|
|
|
2 2 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
dx |
|
|
||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
P |
2 |
|
l M 2 |
|
dx |
|
PP |
|
|
|
|
l M |
M |
|
|
dx P |
2 |
|
|
l M 2 |
dx |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
0 EI |
|
|
|
|
|
|
|
1 2 |
|
|
|
|
0 |
|
|
EI |
|
|
2 |
|
|
0 EI |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
P2 |
|
|
PP |
|
|
P P |
|
|
|
|
P2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
11 |
|
|
|
1 |
2 |
12 |
|
|
|
2 |
|
|
1 |
|
|
21 |
|
|
2 |
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Отже, |
потенціал на |
енергія |
|
|
|
деформації |
є |
квадратичною |
|
формою навантаження. |
В |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
атричній фор і вона оже ути аписана к
|
1 T |
|
|
|
U |
|
P |
B P, |
(5.9) |
2 |
||||
де PT P1 P2 Pn вектор навантажен , B |
атриц податливості. |
|||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
4 |
|||||||||||
Анало ічно ожна |
вира ити |
потенціал ну |
енер ію |
|
. |
|
у |
ви л ді квадратично |
фор и |
|||||||
пере |
і ен . ійсно, підстави о до . |
співвідношенн . |
|
. |
ає |
о |
|
|||||||||
|
|
U |
1 |
K |
T |
B K |
|
1 |
|
T |
K |
T |
BK . |
|
||
|
|
2 |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В |
вши до ува и, |
о внаслідок си |
етрі KT |
K , а до уток |
атриці податливості і |
атриці |
||||||||||
жорсткості дорівнює одиничній |
атриці BK=E, отри ає |
о |
|
|
|
|
|
|||||||||
де |
T |
|
1 |
В ро орнуто
|
U |
1 T K |
|
(5.10) |
|
|
2 |
|
|
2 |
n вектор пере і |
ен , K |
атриц жорсткості. |
|
уви л ді співвідношенн . |
на уває ви л ду квадратично фор |
и пере і ен |
||
U |
1 |
k11 |
2 |
k12 1 2 |
k1n 1 n |
k21 2 1 k |
22 |
2 |
k12 2 n |
|
|
|||||||
|
2 |
1 |
2 |
|
|
|||||||||||||
|
|
|
|
kn1 |
n |
1 |
kn2 |
n 2 |
knn |
2 |
|
|
|
|
|
(5.11) |
||
|
|
|
n . |
|
|
|
|
|
||||||||||
фор |
улює о основні властивості потенціал но |
енер і |
|
|
|
|
|
|
||||||||||
Потенціал на енер і |
дефор аці |
авжди додатна. |
е є наслідко |
співвідношен . і . . |
||||||||||||||
Потенціал на |
енер і |
дефор |
ацій |
є квадратичною |
фор |
ою |
навантаженн |
. |
а о |
|||||||||
квадратичною фор |
ою пере і |
ен |
. 0). |
|
|
|
|
|
|
|
|
|||||||
о потенціал но енер і |
не |
ожна |
астосовувати принцип суперпо иці не алежності дій , |
|||||||||||||||
то то потенціал на енер і дефор |
ацій від ді |
на споруду кіл ко |
навантажен не дорівнює су і |
|||||||||||||||
енер ій від окре о ді кожно о навантаженн . |
|
|
|
|
|
|
|
|
||||||||||
правді, ро |
л не |
о три стани ро т |
нено о стержн . В першо |
у стані на стержен |
діє ро - |
|||||||||||||
т уюча сила P1 |
рис. |
. |
,а , в дру о |
у |
сила P2 |
рис. . , |
, а в трет о у |
о идві сили водночас |
||||||||||
рис. . ,в . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ис. .1 кожно у авантаженні потенціал ну енер ію о числює о а фор улою

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
5 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
l |
N 2 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2EA |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
l P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оді дл першо о |
авантаженн |
U1 |
|
|
1 |
|
|
dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 2EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
l P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дл |
дру о о |
U2 |
|
|
2 |
dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дл |
трет о о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U3 |
l |
P1 P2 2 |
dx |
l |
P12 |
dx |
|
l |
P22 |
|
dx |
|
l |
P1P2 |
dx . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
0 |
|
2EA |
|
|
|
|
|
0 2EA |
|
0 2EA |
|
|
0 |
|
EA |
|
|
||||||||||||||
|
відси випливає, |
о потенціал на енер і |
дефор |
аці |
від одночасно |
ді о о |
сил |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l P P |
|
|
|
|
|
|
|
|
|
|
|
P l |
|
|
|
|
|||||||
|
|
|
|
|
U |
|
|
U |
|
U |
|
|
|
|
1 2 |
dx U |
|
|
U |
|
|
P |
|
2 |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
3 |
|
1 |
|
2 |
|
|
EA |
|
|
|
|
1 |
|
|
2 |
1 EA |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Останній доданок, |
о порушує принцип не алежності дій, |
|
ожна тлу |
ачити |
к ро оту сили P1 |
|||||||||||||||||||||||||||||||
на відповідно у пере |
і енні |
P2l EA, ке |
|
у овлене силою P2 . |
|
к |
|
уло вка ано в п. . , таку |
||||||||||||||||||||||||||||
ро оту на ивают |
ожливою. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поданн |
потенціал но |
енер і у ви л ді квадратично |
фор |
и навантаженн |
. і квадратично |
|||||||||||||||||||||||||||||||
фор |
и пере |
і ен . |
дає |
о у сфор улювати дві важливі теоре |
и. |
|
|
|
|
|
||||||||||||||||||||||||||
Теорема Кастільяно: частинна по ідна від потенціал но |
енер і |
дефор |
аці |
по одній і |
||||||||||||||||||||||||||||||||
діючи не алежни |
у а ал нени |
сил дорівнює пере |
і енню в напр |
|
|
і ціє сили. |
|
|||||||||||||||||||||||||||||
|
асправді, почер ово продиференціювавши квадратичну фор |
у навантаженн . |
по кожній |
|||||||||||||||||||||||||||||||||
діючій силі одержи о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
U |
|
11P1 |
|
12 P2 |
1n Pn , |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
21P1 |
|
22 P2 |
2n Pn , |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
(5.12) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
U |
|
n1P1 |
|
n2 P2 |
n1Pn . |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
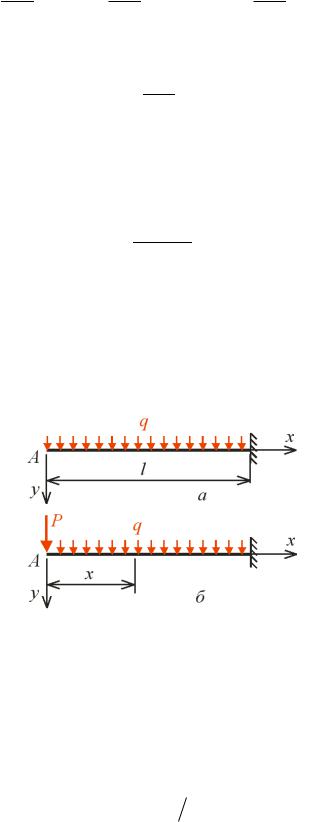
5. Енергетичні теореми і варіаційні принципи |
|
6 |
||
у |
и, о |
ро і ені в правій частині рівностей, вл ют |
со ою |
величини пере і ен |
1, |
2 , , |
n , виражені чере у а ал нені сили і відповідні пере |
і енн |
див. співвідношенн |
. |
. Отже |
|
|
|
|
|
U |
1 , |
U |
|
U |
|
|
|
||||
|
|
P1 |
|
2 |
Pn |
n |
|
|
|||||
|
|
|
P2 |
|
|
|
|
|
|||||
і в а алі |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
i . |
|
|
(5.13) |
||
|
|
|
|
|
|
|
Pi |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е ко впевнитис |
у то |
у, |
о дру а частинна по ідна від |
. |
по кожній у а ал неній силі Pj |
||||||||
дорівнює відповідно |
у одинично |
у пере |
і |
енню |
еле |
енту |
атриці податливості |
|
|
||||
|
|
|
|
|
|
|
2U |
|
ij . |
|
|
(5.14) |
|
|
|
|
|
|
|
|
Pi Pj |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Окре и |
випадко |
теоре и |
астіл |
но є |
теоре а |
ена реа частинні |
по ідні |
від |
|||||
потенціал но енер і дефор |
аці по реакці |
айви |
в |
ей систе |
и дорівнюют нулю. |
|
|||||||
Приклад |
5.1. Ви начити про ин |
віл но о |
кінц |
консол но алки від ді |
рівно |
ірно |
|||||||
ро поділено о навантаженн |
рис. |
. ,а . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
ис. .2 |
|
|
Окрі |
адано о навантаженн , прикладе |
о до віл но о кінц |
А |
алки у а ал нену силу, о |
||
відповідає шукано |
у пере і енню |
вертикал ну силу P рис. . |
, , |
ка фіксує арактер і напр |
||
пере і |
енн . |
|
|
|
|
|
апише о вира |
дл инал но о |
о енту в довіл но у перері і і |
а сцисою x: |
|||
|
|
|
M |
qx2 2 Px . |
|
|

5. Енергетичні теореми і варіаційні принципи |
7 |
Потенціал ну енер ію дефор аці ви начи о а фор улою . |
|
|
|
|
U |
l |
M 2 |
dx |
1 |
|
l qx2 2 Px 2 dx . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
0 |
2EI |
|
2EI |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Виконавши інте руванн , дістане |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
U |
|
|
ql5 |
|
|
|
Pql |
4 |
|
|
P |
2l3 |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
40EI |
|
|
|
8EI |
|
6EI |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вертикал ній осередженій силі відповідає вертикал не пере і |
енн |
точки прикладенн |
сили, |
|||||||||||||||||||||||
то то про ин |
. Відповідно до теоре |
и |
астіл |
но |
. |
|
|
на оди |
о |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
U |
|
|
|
|
ql4 |
|
|
Pl3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
P 8EI 3EI . |
|
|
|
|
|
|
|
|||||||||||
нарешті, поклавши в співвідношенн , |
|
о одержане, дійсну величину допо |
іжно сили P, |
|||||||||||||||||||||||
то то прирівн вши |
до нул , остаточно |
ає |
|
о |
|
|
|
|
ql 4 |
8EI . |
|
|
|
|
|
|
||||||||||
Теорема Лагранжа. |
астинна |
по ідна від |
|
|
потенціал но енер і дефор |
аці |
по одно у і |
|||||||||||||||||||
не алежни |
у а ал нени |
пере |
і |
ен |
дорівнює |
у а ал неній |
силі, |
о |
відповідає |
ц о |
у |
|||||||||||||||
пере і енню. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
правді, продиференціювавши квадратичну фор |
у |
. |
почер ово по кожно |
у не алежно |
у |
|||||||||||||||||||||
у а ал нено |
у пере |
і енню |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
k11 1 |
|
k12 2 |
k1n n , |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
k21 1 |
|
k22 2 |
|
|
k2n n |
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(5.15) |
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
U |
|
kn1 1 |
|
kn2 2 |
|
|
knn n . |
|
|
|
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
і порівн вши |
. |
. |
до оди |
о до висновку, |
о |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
U |
|
|
|
Pi |
. |
|
|
|
|
|
|
|
|
|
(5.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
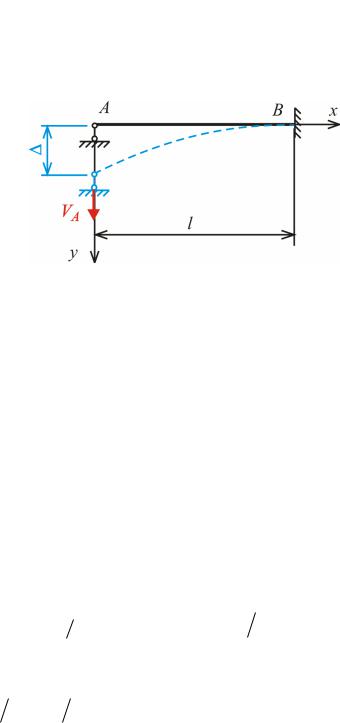
5. Енергетичні теореми і варіаційні принципи |
|
|
|
8 |
||||||
|
е ко впевнитис у то у, о дру а частинна по ідна від |
. |
по не алежно |
у у а ал нено у |
||||||
пере |
і |
енню |
j |
дорівнює силі, ка відповідає ц о |
у пере і |
енню і діє в напр |
і у а ал нено о |
|||
|
|
|
|
|
|
|
|
|
|
|
пере |
і |
енн |
i , то то дру а по ідна від потенціал но енер і |
дефор аці |
дорівнює відповідно у |
|||||
еле |
енту атриці жорсткості |
|
|
|
|
|
|
|||
|
|
|
|
2U |
|
kij . |
|
|
|
(5.17) |
|
|
|
|
i |
|
|
|
|
||
|
|
|
|
j |
|
|
|
|
|
|
Приклад 5.2. О числити реакцію на лівій опорі |
алки |
рис. . |
а у |
ови |
ушено о пере і енн |
|||||
на величину . |
|
|
|
|
|
|
|
|
||
ис. .3 івн нн про инів алки в ра і відсутності ро поділено о навантаженн ає ви л д
|
|
|
|
|
|
|
|
|
|
y C C |
2 |
x C |
3 |
x2 |
C |
4 |
x3. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
Постійні інте руванн |
|
ви начи |
о |
|
ранични |
у ов |
|
|
|
|||||||||||||||
при x=0 |
y(0) |
C1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y 0 |
2C3 |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
при x=l |
y l |
C |
|
C |
2 |
l |
C |
3 |
l 2 |
C |
3 |
l3 |
0 , |
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y (l) C2 2C3l 3C4l 2 |
|
0 . |
|
|
|
|
|
|
|
|
|
||||||||||||
о в |
уючи ці рівн нн , |
на оди |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
C |
, |
|
C |
2 |
|
|
3 2l, |
|
C |
3 |
0, |
C |
4 |
2l3 . |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отже, рівн нн |
пружно ліні |
|
ає ви л д |
|
|
|
|
|
|
|
|
|
||||||||||||
|
y |
1 3x 2l x3 2l3 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
риви на дефор овано осі алки виражаєт с алежністю

5. Енергетичні теореми і варіаційні принципи |
9 |
|
|
|
|
d 2 y |
|
3 |
x l3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Потенціал на енер і |
дефор |
аці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
U |
l |
EI 2 |
dx |
l EI |
|
3 x l3 2 dx |
|
3EI 2 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
2l3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а ал нена сила, |
ка відповідає пере |
і |
|
|
енню |
і є опорною реакцією VA , |
ви начаєт с |
а |
||||||||||||||||||||||
теоре |
ою |
а ранжа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
VA |
|
|
dU |
|
|
3EI |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
5.2. Повна потенціальна енергія деформівної системи |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
процесі дефор |
уванн |
в споруді накопичуєт с |
енер і |
дефор |
аці , |
у овлена внутрішні |
и |
|||||||||||||||||||||||
сила |
и. Однак точки прикладенн |
овнішні |
|
|
сил в процесі дефор уванн |
пере |
і уют с , і то |
у |
|||||||||||||||||||||||
ці сили також |
дійснюют ро оту. В а алі |
|
енер етично точки |
ору дефор уванн |
споруди |
це |
|||||||||||||||||||||||||
процес о |
|
іну енер і |
|
и дво систе |
сил |
|
|
|
овнішні |
і внутрішні . Повна потенціал на енер і |
|||||||||||||||||||||
дефор овано систе и |
оже |
ути представлена у ви л ді |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
A , |
|
|
|
|
|
|
|
|
|
|
(5.18) |
|||
де U |
потенціал на енер і |
дефор |
аці |
ро ота пружни |
|
сил , |
ка |
авжди вважаєт с |
додатною, A |
||||||||||||||||||||||
енер і |
потенціал |
овнішні |
сил, |
ка дорівнює ро оті овнішні |
сил і нако |
" інус". |
|
||||||||||||||||||||||||
Повна енергія деформації |
оже ро |
л датис |
к ро ота, |
ку |
дійснюют |
внутрішні сили |
|||||||||||||||||||||||||
пружності |
і |
овнішнє |
навантаженн |
при |
|
|
пере оді |
систе |
и |
|
дефор |
овано о |
в первісний |
||||||||||||||||||
недефор |
ований стан, внаслідок чо о ро ота внутрішні |
|
сил є додатною, а |
овнішні |
від є ною. |
||||||||||||||||||||||||||
ак, дл |
ро т нено о стержн див.рис. |
|
. ,а потенціал овнішні |
сил |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
P |
|
l |
Pu p . |
|
|
|
|
|
|
|
|
|
||||||
л і нуто алки рис. .
l
A y(x)q(x)dx .
0
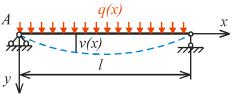
5. Енергетичні теореми і варіаційні принципи |
10 |
ис. .
Потенціал на енер і дефор аці оже ути виражена чере внутрішні сили - дл ро т нени стиснени еле ентів
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U Р |
|
|
|
l |
|
N 2 |
dx , |
|
|
|
|
|
|
|
|
|
|
|
(5.19) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- дл |
і нути |
еле |
ентів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U З |
|
|
|
l |
M 2 |
dx , |
|
|
|
|
|
|
|
|
|
|
|
(5.20) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а о |
ура уванн |
то о, |
о N |
|
EAu , |
M |
|
EIy |
|
чере |
пере |
і енн |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
U |
Р |
1 l |
|
EA u |
|
2 |
dx, |
U |
З |
|
1 l |
EI y |
2 |
dx |
(5.21) |
|||||||||||||||
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
2 |
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
сі ці вира и |
ожут |
ути |
аписані |
|
а єдиною фор ою |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
U C |
|
|
|
U C dx , |
|
|
|
|
|
|
|
|
|
|
|
|
(5.22) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де |
U C |
устина енер і |
дефор |
аці , |
то то енер і , |
о віднесена до довжини стержн , C – |
||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
арактеристика дефор |
івно о стану |
|
ро т |
|
ненн , |
|
ин то |
о . При ро т |
ненні і |
ині |
||||||||||||||||||||||||||
|
|
|
|
|
|
р |
|
N 2 |
|
|
|
|
|
|
u |
|
2 |
|
|
|
|
|
|
З |
|
M 2 |
|
|
|
|
y |
2 |
|
|
||
|
|
|
|
|
U |
0 |
|
|
|
|
|
EA |
|
|
|
|
, |
|
|
U0 |
|
|
|
|
|
|
EI |
|
|
|
. |
(5.23) |
||||
|
|
|
|
|
|
2EA |
|
2 |
|
|
|
|
|
2EI |
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Енер і дефор |
аці |
всіє |
систе и дорівнює су і енер ій |
еле |
|
ентів |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
Ui . |
|
|
|
|
|
|
|
|
|
|
|
|
(5.24) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
|
11 |
|||||
Повна потенціал на енер і |
дефор аці в ра і потре и |
оже |
ути представлена також чере - |
||||
кіл ка |
дискретни пара етрів, |
кі ви начают |
стан усіє |
систе |
и. априклад, дл консол но |
||
алки |
рис. . |
|
|
|
|
|
|
|
П U A 1 l |
EI y 2dx |
l |
q x y x dx Py a M . |
|||
|
|
2 0 |
|
|
|
|
l |
|
|
|
0 |
|
|
|
|
ис. .5 |
|
|
|
Оскіл ки кут повороту є першою по ідною від про инів, то то |
l |
y |
l , ауважи о, о |
повна потенціал на енер і алки алежит від функці про инів y(x) |
к від ар у |
ента. |
|
5.3. Функціонал і варіація
При астосуванні інте рал но о під оду, |
кий |
а уєт с |
на екстре ал ни |
принципа , |
постає |
||||||||||||
нео ідніст |
ро |
л дати про ле у, |
о у а ал нює класичну |
адачу |
ате |
атично о аналі у про |
|||||||||||
пошук |
акси |
ал но о і |
іні ал но о |
начен |
де ко |
функці |
y |
f x , а са |
е, потрі но на одити |
||||||||
акси |
ал ні і |
іні |
ал ні наченн , так вани , |
функціоналів. |
Функціоналом на ивают |
інну |
|||||||||||
величину, наченн |
ко |
ви начаєт с |
аданн |
|
одніє |
а о декіл ко |
функцій. |
ак, функціонало |
|||||||||
оже |
ути довжина l ду и плоско криво , ка |
єднує дві точки A x0 , y0 |
i B x1, y1 рис. . |
||||||||||||||
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 dx . |
|
|
|
|
|
|||
|
|
|
|
|
|
l y x |
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
||
ис. .6
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|||||||||||||||||||||
|
о енти інерці , статичні |
о |
енти, координати центру т жінн |
де ко |
криво |
а о повер ні |
||||||||||||||||||||||||||||
також є функціонала |
и, оскіл ки |
|
наченн |
ви начают с |
|
ви оро |
криво а о повер ні. |
|
|
|||||||||||||||||||||||||
|
всі |
наведени |
|
приклада |
принципови |
є такий факт |
|
к |
о при |
аданні функці |
y |
f |
x |
|||||||||||||||||||||
числу x відповідає число y, то дл функціоналу число відповідає функці . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
е один приклад функціоналу |
ро |
|
л не о потенціал ну |
енер ію дефор |
аці |
алки, |
о |
||||||||||||||||||||||||||
инаєт с |
дефор |
аці |
и |
суву |
дл |
|
спро |
|
енн |
адачі |
|
не тує |
о . |
оді |
ідно |
|
(5.22) |
|||||||||||||||||
потенціал на енер і |
дефор |
аці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
U |
|
l |
EI y |
2 dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина U |
це число, |
ке |
алежит |
від дру о по ідно про инів y |
і, отже, від са |
о функці |
|||||||||||||||||||||||||||
про инів y(x), |
ка |
арактери ує дефор |
овану віс |
алки. |
к |
|
о |
адаватис |
|
рі ни |
и функці |
и |
||||||||||||||||||||||
про инів, |
то кожній функці відповідати |
е своє |
наченн |
|
потенціал но енер і дефор |
аці |
U. |
|||||||||||||||||||||||||||
Отже, потенціал на енер і |
дефор |
аці є функціонало . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ункціонал часто |
адаєт с |
ви начени |
|
інте рало |
. Проте так |
|
уває не |
авжди. |
априклад, |
||||||||||||||||||||||||
координати центру т жінн |
криво чи повер ні ви начают с |
відношенн |
інте ралів. |
|
|
|
||||||||||||||||||||||||||||
|
Варіаційне численн |
вивчає |
етоди, |
кі |
дают |
|
о у |
на одити |
акси |
ал ні |
|
іні |
ал ні |
|||||||||||||||||||||
наченн функціоналів. адачі, в |
ки |
нео |
ідно дослідити де кий функціонал на |
акси |
у |
а о |
||||||||||||||||||||||||||||
іні у , на ивают |
варіаційними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Варіаційна про ле |
а дл |
функціоналу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F x, y, y , y dx |
|
|
|
|
|
|
|
|
|
|
(5.25) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фор улюєт с так |
найти функцію |
y(x) , |
|
а |
ко функціонал П на уває екстре |
ал ні |
іні ал ні |
|||||||||||||||||||||||||||
чи |
акси |
ал ні |
наченн . |
ункці |
y(x) ро шукуєт с |
на |
ножині функцій, |
|
кі |
адані в інтервалі |
||||||||||||||||||||||||
a,b , а також є неперервни |
и і |
|
ладки |
|
и. Всі ці о наки ви начают |
клас функцій, від |
ки |
|||||||||||||||||||||||||||
алежит функціонал. |
а функці , |
кій відповідає ексте |
ал не |
наченн |
функціоналу, на иваєт с |
|||||||||||||||||||||||||||||
екстремаллю. У варіаційно у численні екстремаль віді рає ту са |
у рол , |
о й ар у |
ент функці , |
|||||||||||||||||||||||||||||||
а |
ко о ц |
функці |
ає екстре |
ал не |
наченн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
е ай функціонал . |
|
адано на однопара |
етричній сі |
' |
функцій y x,a . |
О ранн певно о |
|||||||||||||||||||||||||||
числово о |
пара |
етра |
|
одно начно |
ви начає |
криву |
і |
|
сі |
' |
. |
к |
о ви рано |
де кие |
наченн |
|||||||||||||||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
13 |
||||||||||||||||
пара |
етра |
, то функці |
|
y x, |
|
алежит |
лише |
від |
|
одно о |
ар у |
енту |
x, |
|
ожна |
|||||||||||
продиференціювати і підставити одержані величини y x , y x |
і |
y |
|
x |
до функціоналу . . |
|||||||||||||||||||||
оді функці |
F, |
ка на одит с |
під |
нако |
інте ралу, |
алежит |
лише від |
|
інно x, отже |
ожна |
||||||||||||||||
о числити інте рал |
. |
і ви начити число П. |
аки |
чино , |
кожній кривій однопара |
етрично |
||||||||||||||||||||
сі |
' функціонал |
. |
|
ставит |
|
у відповідніст |
де ке число і, |
отже, на однопара етричній сі ' |
||||||||||||||||||
криви |
наченн функціоналу є просто функцією пара |
етра . При де ки |
наченн |
пара |
етра |
|||||||||||||||||||||
ц |
функці |
|
оже на увати стаціонарне наченн . |
риві, відповідні ци |
наченн |
пара |
етра, і |
|||||||||||||||||||
удут |
екстре ал |
и. |
|
л ро |
л нуто |
однопара |
етрично |
сі ' |
|
y x,a |
слід ро рі н ти частинне |
|||||||||||||||
диференціюванн |
по |
|
інній x |
|
при фіксовано |
у пара |
етрі |
і частинне диференціюванн |
по |
|||||||||||||||||
при фіксовано у |
наченні x . Перша операці по начаєт с |
си |
воло |
d, а дру а – си |
воло |
: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dy |
x, |
y dx, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x, |
y d . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иференціал |
y на иваєт с |
варіацією функці |
y x,a |
. Варіаці , |
к і |
уд - кий диференціал, |
|||||||||||||||||||
становит |
со ою лінійну частину прирісту функці , |
о варіюєт с , проте при підра унку варіаці |
||||||||||||||||||||||||
приріст функці о числюєт с |
не від |
інюванн |
ар у |
енту x, |
а від |
інюванн пара етра при |
||||||||||||||||||||
фіксовано |
у x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ро |
л нуто |
у прикладі введенн |
однопара |
етрично |
сі |
' |
y x,a |
дл |
ви наченн |
операці |
||||||||||||||
варіюванн |
|
функці |
у |
овлене лише |
етою поле шити ро у інн |
ново о пон тт . |
а ал но у |
|||||||||||||||||||
випадку цю операцію |
|
ожна ввести наступни |
чино . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
о |
л не |
о де ку функцію y x , ви начену в інтервалі |
a,b |
|
рис. . . |
|
|
|
|
|
|||||||||||||||
ис. .7
о л не о таку інену функцію
~ |
x , |
(5.26) |
y x y x |
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
14 |
|||||||||||||||||||||
де x – де ка функці , |
|
ка |
адовол н є ті ж у |
ови ладкості, |
о й функці |
y |
x . а допо |
о ою |
||||||||||||||||||||
пара етра |
ожна надавати |
|
|
іні функці y |
x |
|
довіл но |
алі величини. |
л |
ц о о достатн о |
||||||||||||||||||
на лижати пара |
етр до нул . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Порівн є |
о |
наченн |
|
інено функці |
~ |
|
|
і |
наченн |
и ви ідно |
функці |
y(x) при де ко у |
||||||||||||||||
|
y x |
|
||||||||||||||||||||||||||
фіксовано у |
наченні |
інно |
x. |
|
|
л |
ц о о ро |
л не |
о рі ницю |
іж |
~ |
і |
y x . О начена |
|||||||||||||||
|
|
y x |
||||||||||||||||||||||||||
рі ниц |
і на иваєт с варіацією функці |
y x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
y |
y |
x |
|
y |
|
x |
|
x . |
|
|
|
|
|
||||||
Варіаці |
арактери уєт с |
дво |
а основни |
и властивост |
|
и. По-перше, |
це нескінченно |
ала |
||||||||||||||||||||
іна, |
оскіл ки пара етр на лижаєт с |
до нул . По-дру е, |
варіаці – це віртуал на ожлива |
|||||||||||||||||||||||||
іна, |
оскіл ки |
ожна |
дійснити довіл ни |
чино . |
|
і ницю |
іж |
варіацією y і диференціало |
||||||||||||||||||||
dy видно на рис. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
к |
о в |
ате |
атично |
у аналі і диференціало |
|
функці f |
на иваєт с |
оловна лінійна частина |
||||||||||||||||||||
приросту функці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f |
|
d f |
|
|
|
|
|
d 2 f |
|
|
|
|
|
d n f |
|
|
Rn 1 , |
|
|
|
|
||||
|
|
|
1! |
|
|
|
|
2! |
|
|
|
|
|
n! |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d f |
|
f |
dx |
|
f |
dy , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
d 2 f |
|
2 f |
|
|
dx2 |
2 |
2 f |
|
dxdy |
2 |
f |
dy2 |
|
|
|
|
|
||||||||
|
|
|
|
x2 |
|
x y |
y2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
то о, то варіаці |
функціоналу |
|
це |
|
оловна лінійна частина приросту функціоналу |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
n |
|
Rn |
1 , |
|
|
|
|
|
|
|||||
|
|
|
|
1! |
|
|
|
|
2! |
|
|
|
|
n! |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
y |
|
|
y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
2 |
|
|
y 2 |
2 |
|
y y |
|
2 |
|
y . |
|
|
|
|
|||||||||
|
|
|
|
|
y2 |
|
|
|
|
|
y y |
|
|
|
|
y 2 |
|
|
|
|
|
|
||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
15 |
||||||||||||||||||
|
аки |
чино |
, варіаці |
функціоналу . |
, |
о |
у |
овлена варіюванн |
|
y і y , ає ви л д |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
F |
y |
F |
y |
d x . |
|
|
|
|
|
|
|
(5.27) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а анало ією |
ате |
атични |
аналі о |
у варіаційно |
у численні |
ає |
ісце наступна теоре а |
|||||||||||||||||||||
к о функціонал |
y x |
|
ає першу варіацію і на уває |
акси |
у |
у а о |
|
іні |
у |
у на де кій кривій |
|||||||||||||||||||
y |
y0 |
x , то перша варіаці |
функціоналу дорівнює нулю, то то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
(5.28) |
||
|
нак |
|
дру о |
варіаці |
функціоналу |
свідчит |
про арактер |
екстре у |
у |
2 |
0 |
|
у ова |
||||||||||||||||
іні |
у |
у, а 2 |
|
0 |
у |
ова |
акси |
|
у |
у функціоналу. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5.4. Необхідна умова екстремуму функціоналу |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Варіаційна |
|
адача, при |
астосуванні до |
адач |
удівел но |
|
е аніки, |
фор |
улюєт с |
в такий |
|||||||||||||||||||
спосі |
ви начити |
де ку |
функцію |
наприклад, |
про ин алки , |
таку, |
|
о и |
функціонал, |
кий |
|||||||||||||||||||
ви начає повну потенціал ну енер ію систе и, |
ав |
и екстре |
у |
, то то |
|
ав стаціонарне |
наченн . |
||||||||||||||||||||||
л |
однови |
ірно о випадку о начений функціонал виражаєт с |
співвідношенн |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
F x, y, y , y dx . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, потрі но, |
о и |
виконувалас |
у ова |
стаціонарності |
функціоналу, |
наприклад, |
у ова |
||||||||||||||||||||||
іні |
у |
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F x, y, y , y dx |
min . |
|
|
|
|
|
|
|
(5.29) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
адоволенн |
у |
ови |
.29 |
нео |
ідно |
ро в |
ати |
адачу |
варіаційно о |
численн |
про |
|||||||||||||||
відшуканн |
екстре |
алі |
y(x) |
дл |
функціоналу |
|
y . |
і |
функцій |
y(x), |
на |
кій шукаєт с |
|||||||||||||||||
екстре |
у |
, |
поки о не ви начена. Природно, |
о функці |
о начено |
сі |
|
ают |
адовол н ти |
||||||||||||||||||||
у ови ладкості, проте крайові у |
ови не вточнюют с . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Припусти |
о, |
о на де кій функці |
y(x) функціонал на уває |
іні |
у |
у. |
о |
л не о на відрі ку |
|||||||||||||||||||||
a,b ра о |
і |
функцією y(x) |
рис. . |
іншу на лижену до не функцію |
|
|
|
|
|
|
|
||||||||||||||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
16 |
|||||||||
|
|
|
|
|
|
y1 |
y |
y, |
|
|
|
|
(5.30) |
де y |
x |
варіаці |
функці |
y; |
ли |
ке до нул |
число, x |
довіл на ладка |
|||||
функці . |
раничні у |
ови, |
ки |
адовол н ют |
функці |
y, |
о |
належат |
до класу |
ожливи |
|||
варіацій V, поки |
е також не уточнюют с . і ни |
наченн |
відповідают рі ні величини П. |
||||||||||
Отже, ожна ро |
л дати П |
к функцію величини . о то |
|
|
|
|
|||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
F x, y x |
x , y x |
x , y x |
x dx . |
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Величина П ати |
е екстре |
ал не |
наченн , |
к |
о |
0 , то |
у |
ає виконуватис у |
ова |
||||
ут по начено
b |
|
|
|
Fy x |
Fy x |
Fy x dx 0. |
(5.31) |
0 a
F |
F , |
F |
F , |
F |
F |
(5.32) |
y |
y |
y |
y |
y |
y |
|
Виконавши інте руванн частина |
и дл |
дру о о і двічі дл |
трет о о доданку в |
.3 дістане о |
||
d d
|
d |
|
|
b |
|
|
b |
|
dFy |
d 2 Fy |
|
|
|
F |
F |
y |
F |
y |
b |
F |
ydx |
0. (5.33) |
|||||
|
|
|
|
|
2 |
||||||||
y |
dx |
y |
|
y |
|
a |
|
y |
dx |
dx |
|
|
|
0 |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||
Перши |
два доданки, то то неінте рал ні члени в |
.3 |
, |
арактери уют |
так |
вані природні |
|||||||||||
раничні у |
ови, то то встановлюют |
в |
ок |
іж функцією y(x) та |
по ідни |
и на |
раниц |
||||||||||
про |
іжку [a,b], а останній інте рал ний доданок |
всередині про іжку. піввідношенн |
.33) |
||||||||||||||
ожна ро |
л дати |
к рівніст нулю ро оти всі |
овнішні |
і внутрішні |
сил, |
о діют |
на пружне |
||||||||||
тіло, на |
ожливи |
пере і енн , ки |
и є варіаці y i |
y . |
кі раничні у |
ови не накладалис |
|||||||||||
на клас V |
ожливи |
варіацій y , серед ни |
існує підклас варіацій V , |
кий складаєт с |
і |
функцій |
|||||||||||
y , |
о |
адовол н ют у ови |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
a |
0, |
y b |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
y |
a |
0, |
y |
b |
|
0. |
|
|
|
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
17 |
а підкласі варіацій V у ова . на уває ви л ду |
|
|
|
|
|
|
|
|
|
|
b |
F |
|
dF |
|
|
|
d 2 F |
y dx |
|
0 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
(5.34) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
dx |
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
варіаційно |
у |
численні |
існує |
|
ле |
а |
к |
|
о |
дл |
уд - |
ко |
неперервно |
на |
відрі ку |
[a,b] |
||||||||||||
функці x виконуєт с |
у |
ова |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
dx |
0, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
x) – також неперервна на відрі ку [a,b] функці , то |
x) |
0. |
|
|
|
|
|
|
||||||||||||||||||||
|
а цій підставі |
оже |
|
о прирівн ти до нул |
вира у дужка |
у співвідношенні .34): |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dF |
|
|
|
d 2F |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Fy |
|
|
y |
|
|
|
|
y |
0. |
|
|
|
|
|
|
|
(5.35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dx2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ей |
вира |
арактери ує |
нео |
ідну |
у ову |
екстре |
ал ності |
функціоналу |
і |
на иваєт с |
||||||||||||||||||
рівнянням Ейлера . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, функці |
y(x), |
ка |
а е печує екстре |
ал ніст |
функціоналу П, |
ає адовол н ти рівн нн |
|||||||||||||||||||||||
(5.35 . |
к |
уло а начено, така функці |
y(x) на иваєт с |
екстре |
аллю. |
|
|
|
|
|
|||||||||||||||||||
|
епер |
поверне |
ос |
|
до |
|
класу |
|
ожливи |
|
|
варіацій |
V. |
|
к |
о |
y(x) |
екстре |
ал , |
то в |
|||||||||
співвідношенні |
. |
інте рал ний член |
е ає і у |
ова |
|
0 на ирає ви л ду |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d F |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П |
F |
|
|
|
y |
|
F |
y b |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
dx |
y |
|
|
|
|
|
y |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
алежно від то о, кі |
раничні у |
ови |
адовол н є функці |
y(x) і відповідно варіаці |
y(x), |
||||||||||||||||||||||||
отри |
ана рівніст |
|
оже |
адавати ти чи інші |
раничні у |
ови, |
о дови начают |
крайову |
адачу. |
||||||||||||||||||||
|
аки |
|
чино , |
астосуванн |
нео |
ідно у |
ови екстре |
у |
у функціоналу дає |
о у |
|
|
|
||||||||||||||||
одержати диференціал не рівн нн |
рівнова и пружно систе |
и, ро в |
ко |
ко о є екстре |
ал |
||||||||||||||||||||||||
ви начити природні |
раничні у ови. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ра і, коли на функці , |
о в од т |
до функціоналу |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
F y1, y2, , yn |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
||||||||
a
накладено додаткові у ови

5. Енергетичні теореми і варіаційні принципи |
18 |
|
|
|
fi y1, y2, , yn |
0 |
|
i |
1,2, , m , |
|
|||
адачу на ивают варіаційною на у овний екстре |
у |
. Вона оже |
ути ведена до варіаційно е |
||||||||
додаткови |
у |
ов дл іншо о функціоналу |
|
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
m fm dx 0 . |
||||
|
|
|
F 1 f1 |
2 f2 |
|||||||
|
|
|
a |
|
|
|
|
|
|
|
|
Екстре |
алі |
дано о функціоналу |
удут |
також |
і |
екстре |
ал |
и |
ви ідно о функціоналу. |
||
Пара етри i |
на ивают с |
неви начени и |
ножника |
и |
а ранжа. Вони |
ожут ути ви начені |
|||||
рівн нн Ейлера та у ов дл |
о ежен |
функцій fi . |
|
|
|
|
|
||||
Приклад 5.3. Одержати рівн нн |
рівнова и |
алки на дво |
опора |
під дією ро поділено о |
|||||||
навантаженн |
рис. .8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. |
.8 |
|
|
|
|
|
|
|
апише |
о повну потенціал ну енер ію дл |
|
алки |
|
|
|
|
|
|
||||
|
l |
EI y |
2 |
|
|
l |
|
|
l |
|
EI y |
2 |
|
|
U A |
|
|
dx |
|
qydx |
|
|
|
qy dx . |
|||
|
2 |
|
2 |
|
|||||||||
|
0 |
|
|
0 |
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
По начи |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F y, y |
|
EI |
y |
2 |
qy . |
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F y, y dx. |
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Використовуючи по наченн |
.32 , |
оже |
о аписати |
|
|
|
|
||||||
|
F |
F |
|
|
|
EI |
y |
2 |
qy |
q , |
|||
|
y |
y |
y |
|
|
2 |
|
|
|
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
19 |
F |
F |
|
EI |
y |
y |
y |
y |
|
2 |
Fy |
F |
|
EI |
y |
y |
y |
|
2 |
2
qy 0 ,
2
qy EIy .
Підставивши одержані величини до рівн нн Ейлера .35 дістане о
|
|
|
|
|
|
q |
|
|
d 2 |
|
EIy |
0 , |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
||||||
то то диференціал не рівн нн |
рівнова и |
алки. |
к о EI |
const , то |
|
|
|
||||||||||||
|
|
|
|
|
|
EI |
|
d 4 y |
q |
0 . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
dx |
4 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
о в |
ок |
дано о |
рівн нн |
ви начит |
|
|
функцію |
про инів, |
ка надаст |
іні |
у у повній |
||||||||
потенціал ній енер і |
алки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
к |
о ро |
л нути неінте рал ні члени, то |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
d F |
|
b |
|
|
|
b |
|
d |
|
|
l |
|
|
|||
|
|
F |
y |
F |
|
y |
0 |
EIy |
y |
EIy y |
l |
||||||||
|
|
y |
dx |
y |
|
y |
|
|
|
|
a |
|
dx |
|
|
0 |
|
0 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
EIya y EIyb y EIyb y EIya y 0.
|
онкретний ви л д природни |
|
ранични |
у |
ов алежит |
від типу кіне |
атични |
ранични |
||||||||||||||
у ов |
алки. |
іне |
атичні |
раничні у |
ови |
адают |
варіаці |
v |
0 |
, v l |
і v |
0 |
, v |
l , кі, |
||||||||
в свою чер у, |
адают |
природні |
раничні у |
ови. |
ожливі варіанти наведено у |
веденій та лиці |
||||||||||||||||
5.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, крайова |
адача, |
о описує |
ин |
алки, ви начаєт с |
навантаженн |
q x , |
а також |
|||||||||||||||
кіне |
атични |
и і |
природни |
и |
ранични и |
у |
ова |
и. |
алежно |
від |
ранични |
|
у |
ов |
ожна |
|||||||
ро рі н ти два типи |
адач. В |
адача |
першо о типу ро в' |
ок існує при |
уд - |
ко у ро поділено у |
||||||||||||||||
навантаженн |
q x . |
В |
адача |
дру о о |
типу ро в' |
ок |
існує |
тіл ки |
тоді, |
коли |
навантаженн |
|||||||||||
адовол н є додаткові у |
ови. Ви начал ни |
в дано |
у випадку є |
арактер ро в' |
ку рівн нн |
|||||||||||||||||
рівнова и однорідно |
адачі |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
EIyIV 0

5. Енергетичні теореми і варіаційні принципи |
20 |
||
відповідни |
и ранични и |
у ова и. к о крайова однорідна адача |
ає лише тривіал ний |
ро в' ок, то |
вона належит |
до першо о типу. В протилежно у ра і – |
до дру о о. о л не о |
о начене питанн докладніше. |
|
|
о в' ок однорідно о рівн нн |
ви начаєт с |
співвідношенн |
y0 x C1Y1 x C2Y2 x C3Y3 x C4Y4 x , |
||
де C1,C2 ,C3,C4 – константи, |
кі ви начают с |
ранични у ов, а Y1 x ,Y2 x ,Y3 x ,Y4 x – |
фунда ентал на систе а функцій |
|
|
|
|
|
|
|
|
Y x |
1, Y x x, Y x |
|
x2 |
, |
Y x |
x3 |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
3 |
|
|
|
2! |
|
4 |
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
е ко впевнитис , |
о дл |
ранични |
у |
ов |
ео |
етрично не |
інювани |
алок див. р дки |
– 4 |
||||||||||||||
та |
л. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
C2 |
|
C3 |
|
C4 |
|
|
0, |
|
|
|
|
|||
то то дл |
а начени с е |
y0 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
л |
|
ео |
етрично |
інівано |
алки, |
|
о ає лише одну шарнірну опору |
див. р док та л. . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
C1 |
C3 |
|
C4 |
|
|
|
0. |
|
|
|
|
|
|
||
|
аки |
чино |
, нетривіал ний ро в' |
ок дл |
ціє |
алки |
|
ає ви л д |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
y0 x C2Y2 x C2 x, |
|
|
|
|
||||||||||||
де C2 – довіл на константа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
л |
неоперто |
алки р док |
та л. . |
|
існуют |
два нетривіал ні ро в' |
ки. е ко впевнитис |
в |
||||||||||||||||
то |
у, |
о |
|
y(1) |
C |
(C |
|
ожна в |
ти таки |
|
, |
|
о дорівнює 1), |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0(2) |
C2 x |
(C2 |
ожна в |
ти таки |
|
, |
|
о дорівнює . |
|
||||||||||
|
Ви начи |
о надалі ро в' |
ок неоднорідно о рівн нн |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
EIyIY |
q x . |
|
|
|
|
|
|
|
|
|||||
|
івн нн |
адовол н єт с частинни |
|
ро в' |
ко |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y x |
|
|
1 x |
x f |
|
d , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
3! 0 |
|
|
|
|
||||||||||
де |
f |
|
|
q x |
EI . |
ей ро в' ок |
кий відповідає початкови |
у ова |
|
|
||||||||||||||
y 0 y 0 y 0 y 0 0.
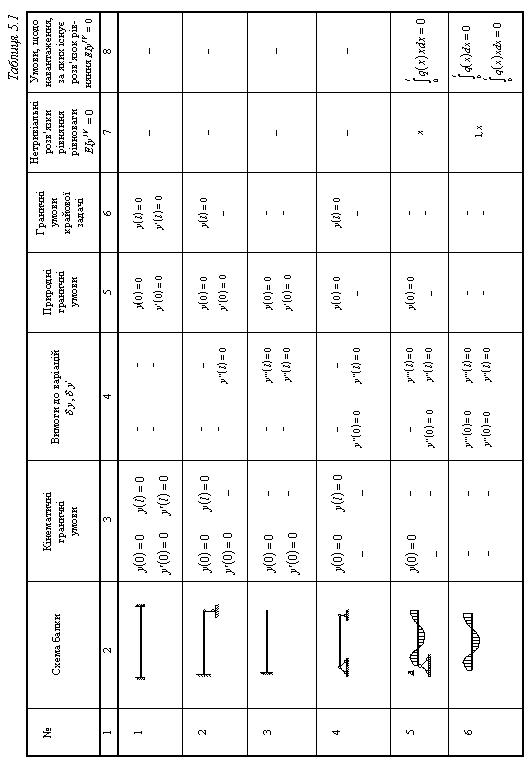
5. Енергетичні теореми і варіаційні принципи |
21 |
5. Енергетичні теореми і варіаційні принципи |
22 |
а ал ний ро в' ок неоднорідно о рівн нн апишет с |
к су а ро в' ків однорідно о і |
неоднорідно о рівн н |
|
y x C1Y1 x C2Y2 x C3Y3 x C4Y4 x y x .
Проаналі ує |
о |
астосуванн |
а начено о ро в' ку дл |
рі ни |
ранични у |
ов. |
|
|||||
л |
алки, |
о |
ає |
атисненн |
о о сторін |
див. р док |
та |
л. . |
, на підставі ранични |
у ов |
||
на ліво |
у кінці |
x=0), |
ає о C1 |
0, C2 0. |
апише |
о |
раничні у |
ови дл |
право о кінц |
x=l): |
||
|
|
|
|
y l |
|
C3Y3 l C4Y4 l |
y l |
|
0, |
|
||||||||||||||||
|
|
|
|
y l |
|
C3Y3 l C4Y4 l |
y l |
|
0. |
|
||||||||||||||||
Отже, |
ає о систе |
улінійни |
ал е ра чни |
рівн н відносно довіл ни |
констант |
|||||||||||||||||||||
|
|
|
|
|
|
Y3 l |
|
Y4 l |
C3 |
|
|
|
y |
l |
|
|
|
|||||||||
|
|
|
|
|
|
Y3 l |
|
Y4 l |
C4 |
|
|
|
y |
l |
|
|
|
|||||||||
а о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
l3 |
|
|
|
|
|
|
1 |
|
|
|
|
l |
3 f d |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|||||||||
|
|
|
|
C3 |
3! |
|
||||||||||||||||||||
|
|
|
2! |
|
3! |
|
0 |
|
|
|
|
. |
|
|||||||||||||
|
|
|
|
|
|
l 2 |
C4 |
1 |
|
|
|
|
l |
|
|
|
|
|||||||||
|
|
|
|
l |
|
|
|
|
2 f |
d |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|||||||
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2! 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Оскіл ки ви начник |
атриці коефіцієнтів не дорівнює нулю |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
|
l3 |
|
|
|
|
|
l 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Det |
|
2! |
|
3! |
|
|
|
|
|
0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l |
|
l 2 |
|
|
|
12 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
систе |
а |
ає один і тіл ки один ро в' |
ок при |
уд - кій функці |
|
f |
x . |
|
||||||||||||||||||
л |
алки, атисненою на ліво у і шарнірно опертою на право |
у кінці |
див. р док та л. . ), |
|||||||||||||||||||||||
також |
ає о C1 0, |
C2 0. |
ранични у |
ов дл право о кінц x=l) |
ає о |
|||||||||||||||||||||
|
|
|
|
y l |
C3Y3 l C4Y4 l |
y l |
|
0, |
|
|||||||||||||||||
|
|
|
|
y l |
|
C3Y3 l C4Y4 l |
y l |
|
0. |
|
||||||||||||||||
Відносно констант C3,C4 отри ає о систе у

5. Енергетичні теореми і варіаційні принципи |
23 |
Y3 |
l |
Y4 |
l |
C3 |
y |
l |
Y3 |
l |
Y4 |
l |
C4 |
y |
l |
а о ура уванн начен фунда ентал но систе и функцій |
|
|||||
|
|
|
|
l2 |
|
l |
3 |
C3 |
|
|
|
|
|
1 l |
l 3 f |
d |
|
|
|||||||||
|
|
|
|
2! |
3! |
|
|
|
|
3! 0 |
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
C4 |
|
|
|
|
l |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
l |
|
|
|
|
|
|
|
l |
|
f |
|
d |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ви начник |
атриці коефіцієнтів від інний від нул |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
l3 |
|
|
|
l |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Det |
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2! |
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
відси випливає, |
о |
адача |
ає ро в' |
ок при |
|
уд - |
кій функці |
f x . |
|
|
|||||||||||||||||
Анало ічна ситуаці |
ає |
ісце в |
алка , |
о |
|
ают |
|
атиснени |
лівий і не |
акріплений правий |
|||||||||||||||||
кінец |
див. р док |
та |
л. . |
а о о идва шарнірно оперти |
кінц |
див. р док |
та л. . . |
||||||||||||||||||||
нша ситуаці |
виникає при аналі і |
ео |
етрично |
інювано |
алки, ка |
ає шарнірну опору при |
|||||||||||||||||||||
x 0 і віл ний кінец |
при x |
|
l |
|
див. р док |
та л. |
. |
|
. |
|
л ліво о кінц |
алки ранични у ов |
|||||||||||||||
ожна |
аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
C3 |
0. |
|
|
|
|
|
|
|||||||||
раничні у ови на право у кінці
y l |
C2Y2 l C4Y4 l |
y l |
0, |
y l |
C2Y2 l C4Y4 l |
y l |
0. |
Перепише о систе у в атричній фор і
|
|
|
l |
|
|
|
0 |
l |
C2 |
l |
|
f |
d |
0 |
|
|
. |
|||
0 |
1 |
C4 |
l |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
f |
|
d |
|
|
|
|
0 |
|
|
|
Ви начник атриці коефіцієнтів дорівнює нулю
5. Енергетичні теореми і варіаційні принципи |
24 |
|
|
Det |
0 |
l . |
0 |
|
|
|
|
0 |
1 |
|
|
і, отже, систе а |
оже ати ро в' ок |
лише |
в |
ра і |
виконанн певни у ов. ійсно, систе а |
|
складаєт с дво |
рівн н |
|
|
|
|
|
|
|
l |
|
|
|
|
|
lC4 |
|
l |
f |
|
d , |
|
|
0 |
|
|
|
|
|
|
l |
|
|
|
|
|
C4 |
f |
|
d . |
|
|
|
|
0 |
|
|
|
|
l
О идві рівності ожливі одночасно, к о
f |
d 0, то то навантаженн |
ає |
|
|
|
|
|
|
|
0 |
|
|
|
|
адовол н ти рівн нн |
рівнова и |
M A 0. |
При ц о |
у константа C2 |
оже |
ути довіл ною, |
|||||
то то |
алка |
оже ати |
уд - кий поворот відносно шарніра. |
|
|
|
|||||
о |
л не |
о |
неоперту |
алку |
див. р док |
та л. . |
. |
ранични |
у ов |
на ліво у кінці |
|
C3 |
C4 |
0. |
апише |
о у |
ови на право у кінці |
|
|
|
|
|
|
|
y l |
C1Y1 l C2Y2 l |
y l |
0, |
||||
|
y l |
C1Y1 l C2Y2 l |
y l |
0. |
||||
і співвідношенн ожна перетворити до наступно о ви л ду |
|
|||||||
|
|
l |
|
|
|
|
|
|
|
|
l |
|
f |
d |
0, |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
f |
d |
0, |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
відки випливає, |
о |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
f d |
0. |
|
|
|||
|
|
0 |
|
|
|
|
|
|
Отже, ожна |
ро ити висновок, |
о функці |
f |
|
ає |
адовол н ти дві у ови: |
||
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
25 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
d |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
d |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то то |
навантаженн |
повинно |
ути |
са |
о рівноважени |
. |
онстанти |
C1 , |
C2 |
ожут |
|
ути |
|||||||||||||||||
довіл ни |
и. |
е о начає, |
о дефор |
ована |
алка |
оже |
ай ати |
уд - ке положенн на пло ині. |
|
||||||||||||||||||||
5.5. Варіаційна постановка задачі про плоский згин |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
к |
уло ска ано, |
одна й та ж са |
а |
адача статики дефор івни |
систе |
|
ате |
атично |
оже |
ути |
|||||||||||||||||||
поставлена по рі но |
у. |
ласична постановка |
|
вл є со ою крайову |
адачу дл |
диференціал ни |
|||||||||||||||||||||||
рівн н , |
адани |
в де кій о ласті. |
івн нн |
становл т |
|
три |
рупи, |
о |
арактери уют |
напружено- |
|||||||||||||||||||
дефор |
ований стан дефор |
івно |
систе |
и всередині о ласті. |
райові у |
ови адают с |
|
на |
раниці |
||||||||||||||||||||
о ласті і |
ожут |
ви начатис |
ранични |
и рівн нн |
и і |
ранични |
и у |
ова |
и. |
|
|
|
|
|
|||||||||||||||
Ви од чи |
першо |
постановки |
адачі |
статики |
|
а |
допо |
о ою |
|
операцій інте руванн |
і |
||||||||||||||||||
варіюванн |
шукано |
функці |
|
ожна |
прийти |
до |
дру о |
постановки. |
|
к |
о |
перша |
|
постановка |
|||||||||||||||
на иваєт с диференціал ною, то дру ий під ід носит |
|
на ву варіаційно о. Основною процедурою |
|||||||||||||||||||||||||||
пере оду від диференційно |
постановки до варіаційно |
є інте руванн |
а частина и. |
|
|
|
|
||||||||||||||||||||||
іншо о |
оку, |
ожна |
|
а ви ідну в ти варіаційну |
адачу і далі, використовуючи відповідні |
||||||||||||||||||||||||
положенн варіаційно о численн , |
перейти до крайово |
адачі. |
|
дано |
у випадку диференціал не |
||||||||||||||||||||||||
рівн нн |
є рівн нн |
Ейлера дл |
варіаційно |
|
адачі. |
|
а начений фор |
алі |
пере одів від одніє |
||||||||||||||||||||
постановки до іншо |
оже |
ути |
астосований в |
адача |
|
статики дл |
рі ни |
дефор івни |
тіл, у то у |
||||||||||||||||||||
числі |
дл |
пластин, |
о олонок, |
стержневи |
систе |
то |
о. |
о |
л не |
о |
всі |
ці |
питанн |
на |
адачі |
||||||||||||||
плоско о |
ину пр |
олінійно о стержн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5.5.1 Основні співвідношення задачі про плоский згин прямолінійного стержня |
|
|
|
|
|||||||||||||||||||||||||
е ай до пр |
олінійно о стержн постійно |
жорсткості EI прикладено поперечне ро поділене |
|||||||||||||||||||||||||||
навантаженн |
q(x). |
а рис. |
. |
,а пока ано додатні напр |
|
и осей координат, а на рис. . |
, |
– додатні |
|||||||||||||||||||||
напр |
и |
инал ни |
о ентів M і поперечни |
сил Q. |
інці стержн |
|
ро ташовані в точка |
||||||||||||||||||||||
координата |
и x=a i x=b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
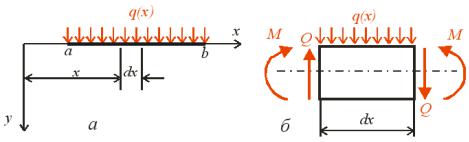
5. Енергетичні теореми і варіаційні принципи |
26 |
ис. .
апружено-дефор ований стан стержн описуєт с тр о а рупа и рівн н . Перша рупа – це рівн нн рівнова и, віднесені до внутрішні точок стержн
|
dQ |
q, |
dM |
Q, x |
a,b . |
(5.36) |
|
dx |
dx |
||||
|
|
|
|
|
||
о дру о рупи в од т ео етричні рівн нн , |
о пов' |
уют дефор аці і пере і |
енн |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 y |
x |
a,b , |
|
|
|
(5.37) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де |
y x |
– пере і |
енн |
точок осі стержн в довж осі y, x – дефор аці |
ину, |
ка |
вл є со ою |
||||||||||||||||||
криви ну осі стержн |
в перері і |
а сцисою x. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
івн нн |
трет о |
|
фі ично |
|
рупи встановлюют |
в' |
ок іж дефор |
аці и і внутрішні |
и |
|||||||||||||||
усилл |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
EI . |
|
|
|
|
|
|
(5.38) |
|||
|
аведені |
співвідношенн |
|
|
. |
– |
|
. |
|
|
|
ви начают |
напружено-дефор |
ований стан |
у |
||||||||||
внутрішні |
точка |
стержн . |
л |
отри |
анн |
крайово |
адачі ці рівн нн |
нео |
ідно доповнити |
||||||||||||||||
ранични и у ова и. |
л ц о о на ліво |
у (x=a) і на право |
у (x=b) кінц |
стержн |
ставл т с |
по |
|||||||||||||||||||
дві раничні у ови. |
а ліво |
у кінці |
ожут |
ути |
|
адані чотири варіанта у |
ов |
|
|
|
|
||||||||||||||
1) |
кіне |
атичні у ови – пере |
і |
енн |
y a і кут повороту y |
x ; |
|
|
|
|
|
||||||||||||||
2) |
природні у ови – поперечні сили Q a і |
|
инал ні о |
енти M a ; |
|
|
|
|
|
||||||||||||||||
3) |
ішані у |
ови |
y a |
і M a ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
ішані у |
ови |
y a |
і Q a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Анало ічн варіанти у ов |
|
ожут |
адаватис |
на право |
у кінці стержн |
y b |
i |
y |
b ; |
|
||||||||||||||
2) |
Q b |
i M b ; |
3) |
y b |
i |
M b ; |
4) |
y b |
|
|
i Q b . |
|
ови на ліво |
у і право |
у кінц |
не |
|||||||||
алежат |
одне від одно о. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

5. Енергетичні теореми і варіаційні принципи |
27 |
л ручності фор улюванн ранични у ов введе о си волічні вектори |
операцій |
диференціюванн |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
dx . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
d |
|
d |
|
d |
2 |
|
|
|
|
|
|
|
|
(5.39) |
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
а допо |
о ою ци |
си |
волічни |
векторів кіне атичні і природні |
раничні у |
ови |
ожут |
ути |
|||||||||||||||||||
представлені вира а |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
d1y, |
M |
|
d2M . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При фор |
улюванні |
ішани |
ранични |
у |
ов скористає |
|
ос |
під одо , викладени |
в ро оті |
|||||||||||||||||||
проф. .А. |
о іна [29]. Введе |
|
о спеціал ні діа онал ні |
атриці дру о о пор дку |
I1 |
i |
I2 , у |
|||||||||||||||||||||
ки |
кожен діа онал ний еле |
ент дорівнює а о нулю а о одиниці, |
а су а ци |
дво |
атриц |
|||||||||||||||||||||||
дорівнює одиничній |
атриці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
I1 |
I2 |
|
1 |
0 |
. |
|
|
|
|
|
|
|
|
|
(5.40) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Отже, |
к |
о кійс |
діа онал ний еле |
ент |
атриці I1 |
дорівнює одиниці, то відповідний еле ент |
||||||||||||||||||||||
атриці I2 дорівнює нулю і навпаки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
а допо |
о ою атриц |
d1,d2 ,I1,I2 |
чотири варіанта |
ранични |
у |
ов на ліво у кінці стержн |
|||||||||||||||||||||
при x |
a) |
апишут с |
а єдиною фор |
ою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
I1d1y x |
I2d2M x x a |
v a |
p a , |
|
|
|
|
(5.41) |
|||||||||||||||
де дл першо о варіанта |
ранични |
у ов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
I1 |
1 |
0 |
|
|
I2 |
0 |
0 |
|
|
|
|
|
y a |
|
|
|
0 |
|
|
|
|
||||
|
|
|
0 |
1 |
, |
|
0 |
0 |
, |
|
v a |
|
y |
a |
, |
p a |
0 |
; |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
дл |
дру о о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
0 |
0 |
|
|
I2 |
1 |
0 |
|
|
|
|
|
0 |
|
|
|
|
Q a |
|
|
|
|
|
||
|
|
|
0 |
0 |
|
, |
0 |
1 |
, |
|
v a |
|
0 |
, |
p a |
|
M a |
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

5. Енергетичні теореми і варіаційні принципи |
28 |
дл трет о о |
|
|
|
|
I1 |
1 |
0 |
|
I2 |
|
0 |
0 |
|
|
|
y a |
|
|
|
0 |
|
|
|
|
|
0 |
0 |
, |
|
0 |
1 |
, |
v a |
|
0 |
, |
|
p a |
M a |
; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
і дл |
четверто о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
I1 |
0 |
0 |
|
I2 |
|
1 |
0 |
|
|
|
0 |
|
|
|
Q a |
|
|
|
|
|
0 |
1 |
, |
|
0 |
0 |
, |
v a |
|
y |
a |
, |
p a |
|
0 |
; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
наведени |
співвідношенн |
вектори ν i |
p введено дл |
|
ожливості |
апису ранични у ов |
|||||||||||||
а єдиною фор |
ою дл всі |
варіантів. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
а право у кінці стержн |
x |
b |
раничні у ови |
апишут с |
у ви л ді |
|
|
|
|||||||||||
|
|
|
|
|
I1d1y x |
I2d2M x x |
b |
v b |
p b . |
|
|
(5.42) |
||||||||
|
атриці I1, I2 |
і вектори ν, p ви начают с |
так са |
о, к і дл |
ліво о кінц |
стержн . |
||||||||||||||
|
аки |
чино |
, крайову |
адачу дл |
ину стержн |
ожна |
аписати к систе |
у рівн н стосовно |
||||||||||||
пере |
і |
ен , дефор |
ацій і внутрішні |
усил |
|
|
|
|
|
|
|
|
|
|
||||||
d 2 M |
q |
x |
|
dx2 |
|||
|
|
||
|
d 2 y |
; |
|
|
dx2 |
|
|
M |
EI |
|
ранични у ова и
I1d1y x I2d2M x
I1d1y x I2d2M x
0;
(5.43)
x |
a |
v a |
p a ; |
|
|
||
|
|
|
(5.44) |
x |
b |
v b |
p b . |
|
|
5. Енергетичні теореми і варіаційні принципи |
29 |
Отже, крайова адача повністю ви начаєт с авданн функці q x , жорсткості EI , векторів
v a , p a , v b , p b , а також атриц I1 |
|
а о I2 |
на кожно у кінці стержн . |
|
|||||||||||||
Виключивши в систе і |
. |
дефор |
ацію , |
ожна перейти до постановки |
адачі відносно |
||||||||||||
пере і ен |
і |
инал ни |
о |
ентів M x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
d 2M |
|
q(x) 0, |
|
|||||||
|
|
|
|
|
|
|
dx2 |
|
(5.45) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
d 2 y |
|
|
M |
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
dx2 |
|
EI |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
ранични |
и у |
ова |
и . . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, |
о в |
адачі (5.45) |
ожна виключити внутрішні усилл M x і |
аписати крайову |
|||||||||||||
адачу відносно пере |
і |
ен |
y x : |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
d 4 y |
q x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
’ |
(5.46) |
||||
|
|
|
|
|
|
|
|
|
dx4 |
EI |
|||||||
I1d1y x I2d2M x x a
I1d1y x I2d2M x x b
v a |
p a , |
|
(5.47) |
v b |
p b . |
5.5.2 Формула Гріна для задачі про плоский згин |
|
|
|
|
|
|
|
|
|
||||||
ор |
ула |
ріна вл є со ою фор улу інте рал но о численн , |
ка пов' |
ує |
наченн |
n-кратно о |
|||||||||
інте рала по |
де кій о ласті і |
n-1)-кратно о інте рала по |
раниці |
ціє |
о ласті. |
ор |
ула |
ріна |
|||||||
широко |
використовуєт с |
в |
ате атичній фі иці при |
по удові і |
при |
дослідженні |
ро в' |
ків |
|||||||
крайови |
адач. По удова |
фор ули |
дл |
адачі про |
ин |
стержн |
водит с до |
двократно о |
|||||||
інте руванн |
а частина и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е ай на |
інтервалі |
a,b |
адано |
дві |
функці f |
x |
i |
g x , |
кі |
ожут |
|
ути |
двічі |
||
продиференційовані всередині інтервалу. Використовуючи фор |
улу інте руванн |
а частина и |
|||||||||||||
ожна аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Енергетичні теореми і варіаційні принципи |
30 |
b |
d 2 g x |
|
|
dg x |
|
b |
b df x dg x |
|
|
||||
|
|
|
|
|
|||||||||
f x |
|
dx f |
x |
|
|
|
|
|
|
|
|
dx . |
(5.48) |
dx2 |
dx |
|
a |
|
dx |
|
dx |
||||||
a |
|
|
|
a |
|
|
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Післ повторно о інте руванн а частина |
и одержи |
о |
|
|
|
|
|
||||||
b |
f x |
d 2 g x |
dx f x |
dg x |
|
b |
|
||||||
|
|
|||||
a |
dx2 |
dx |
|
a |
||
|
|
|
||||
|
|
|
||||
|
|
|
|
|
|
df x |
g x |
|
b |
b |
d 2 f |
|
x |
g x dx . |
(5.49) |
|
|
||||||||
|
|
|
|
||||||
dx |
|
a |
a |
dx |
2 |
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Використовуючи диференціал ні оператори . |
, рівніст (5.49) |
|
ожна аписати у ви л ді |
|||||||||||||||||||||
|
|
|
|
|
b |
|
|
d 2 g x |
|
d 2 f x |
|
|
|
|
|
|
|
|
T |
|
b |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
f |
x |
|
|
|
|
|
|
|
g x |
dx |
d2 |
f x |
|
d1 g x |
|
, |
(5.50) |
|||
|
|
|
|
|
|
dx2 |
|
|
dx2 |
|
|
||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де в правій частині |
аписано скал рний до уток векторів d2 f |
x |
i |
d1 g x . піввідношенн |
|||||||||||||||||||||
. |
становит |
фор улу |
|
ріна дл |
адачі, |
о о |
|
оворюєт с . |
|
|
|
|
|
|
|||||||||||
|
о |
л не о де кі осо ливості, пов' |
ані і |
|
астосуванн |
ціє |
фор |
ули до функцій |
инал ни |
||||||||||||||||
о |
ентів |
M x |
і |
пере |
і ен |
y x , |
кі фі уруют |
у |
крайовій |
адачі . |
, . |
. ункці |
|||||||||||||
инал ни |
о |
ентів, дефор |
ацій |
і |
пере |
і |
ен , |
|
кі |
адовол н ют крайові |
адачі, на ве о |
||||||||||||||
дійсни |
и і по начи |
о |
відповідно M0 x , 0 |
x |
i |
y0 |
x . Пор д |
|
дійсни и введе |
о статично |
|||||||||||||||
ожливу функцію |
инал ни |
о ентів M 0 |
x , |
|
ка |
|
адовол н є тіл ки рівн нн |
рівнова и |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d 2M 0 |
x |
q x |
0 |
|
|
|
|
|
(5.51) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
і природні раничні у ови
|
0 |
x |
|
|
|
|
|
|
|
||||
I2d2M |
|
|
|
x a |
||
|
0 |
|
|
|
||
x |
||||||
|
|
|||||
I2d2M |
|
|
x b |
|||
|
|
|
|
|
||
p a ;
|
(5.52) |
p b . |
|
а |
підставі теоре и єдності ро в' |
ку |
крайово адачі |
. , |
. |
дійсні |
усилл |
M0 x , |
дефор |
аці 0 x і пере і енн |
y0 x |
ви начают с |
єдини |
чино . |
о о не |
ожна |
|

5. Енергетичні теореми і варіаційні принципи |
|
|
|
31 |
|||||||
стверджувати |
про |
статично ожливі |
инал ні о |
енти M 0 |
x . |
Останні |
єдини |
чино |
|||
ви начают с |
лише |
в статично ви начувани |
систе |
а , оскіл ки |
дл |
таки |
систе |
ро в' ок |
|||
крайово адачі . |
, . |
є єдини . |
|
|
|
|
|
|
|
||
о |
л не |
о, наприклад, |
стержен (рис. . |
, віл ний на ліво у кінці x=a) |
і атиснений на |
||||||
право |
у кінці x=b). |
е ео |
етрично не |
інювана і статично ви начувана систе а. |
|
||||||
ис. .10
В дано у випадку на ліво у кінці
|
I2 |
1 0 |
|
|
0 |
|
|
|
0 |
1 |
, |
p a |
0 |
, |
|
|
|
|
|
|
|||
а на право у кінці |
|
|
|
|
|
|
|
|
I2 |
0 0 |
|
|
0 |
|
|
|
0 |
0 |
, |
p b |
0 |
. |
|
|
|
|
|
|
|||
Отже, систе а . , . |
становит |
адачу |
оші дл вичайни диференціал ни рівн н , у |
||||
ки при x=a адано M a |
0 i M a |
0. |
ожливі |
вони ж і дійсні усилл |
|||
|
|
|
|
x |
|
|
|
|
M 0 x |
|
|
|
x |
q |
d . |
a
л стержн , віл но оперто о на ліво у кінці x=a, і атиснено о на право у x=b рис. . ,
ис. .11
ає о дл ліво о кінц
I2 |
1 |
0 |
, |
|
0 |
|
0 |
0 |
p a |
0 |
, |
||
|
|
|
|
|||
а дл право о |
|
|
|
|
|
|
I2 |
0 |
0 |
, |
|
0 |
|
0 |
0 |
p b |
0 |
. |
||
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
32 |
||||||||||||
|
тержен |
становит |
|
статично |
неви начувану систе у. |
Внаслідок |
ц о о |
в дано |
у випадку |
||||||||||
ає |
о справу і |
адачею |
оші, дл |
ко |
недови начені початкові |
у ови |
адано |
M a і |
не |
||||||||||
ви начено по ідну |
M a . В цій статично неви начуваній |
адачі систе |
а співвідношен |
. |
, |
||||||||||||||
. |
ви начає цілу сі |
'ю статично |
ожливи |
усил |
M 0 x . В силу 5.43 |
дл |
кожно о статично |
||||||||||||
ожливо о |
усилл |
M 0 |
x |
ожна поставити у відповідніст |
дефор ацію |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
x |
1 |
M 0 x . |
|
|
|
|
(5.53) |
||
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При варіаційно |
у фор |
улюванні |
адачі про |
ин стержн |
використовуєт с |
сі ' кіне |
атично |
||||||||||||
ожливи пере і |
ен |
y* |
x . |
о ціє |
сі ' належит |
функці , кі не порушуют |
суціл ності алки |
||||||||||||
в інтервалі |
a,b , |
то то |
ают |
неперервну першу по ідну і |
адовол н ют |
кіне атичні у |
ови на |
||||||||||||
кінц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1d1y* x I1d1y* x x a
x b
першо у ро л нути стержнів рис. . |
ає о |
при x=a |
|
v a ,
|
(5.54) |
v b . |
|
I1 |
0 |
0 |
|
0 |
|
0 |
0 |
, v a |
0 |
; |
|
|
|
|
при x=b
I |
1 |
0 |
, |
|
0 |
; |
|
|
v b |
|
|||
1 |
0 |
1 |
|
|
0 |
|
|
|
|
|
дру о у стержні рис. . ): при x=a
I1 |
1 |
0 |
|
0 |
|
0 |
0 |
, v a |
0 |
; |
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
33 |
||||||
при x=b |
|
|
|
|
|
|
|
I1 |
1 |
0 |
|
0 |
|
||
0 |
1 |
, v b |
0 |
. |
|||
|
|
|
|
||||
ожно у кіне атично ожливо у пере |
і |
енню y* |
x |
у силу 5.43 ожна поставити у |
|||
відповідніст дефор ацію |
|
|
|
|
|
|
|
|
* x |
|
d 2 y x |
|
(5.55) |
||
|
|
dx2 |
|||||
|
|
|
|
|
|||
та усилл |
|
|
|
|
|
|
|
|
M * |
x |
EI * |
x . |
(5.56) |
||
Природно, |
о дійсні |
усилл |
|
M 0 |
x |
належат |
до класу статично |
|
ожливи |
усил , |
а дійсні |
||||||||||||||||||||||||
пере і |
енн |
|
y0 x – до класу кіне |
атично |
ожливи |
пере |
і |
ен . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ор |
ула |
ріна |
|
5.50 |
справедлива дл |
|
уд - |
ки |
двічі |
диференційовани |
|
функцій |
f |
x i |
|||||||||||||||||||||
g x . |
к о підпор дкувати ці функці |
де ки |
додаткови |
|
у ова |
, |
прита |
анни |
ро |
л нутій |
|||||||||||||||||||||||||
адачі, наприклад, покласти f x |
|
M 0 |
x , |
а |
g x |
y* |
|
x , то і |
співвідношенн |
|
. |
ожна |
|||||||||||||||||||||||
одержати |
одифікацію |
фор |
ули |
|
ріна, |
|
ка пов' |
ує статично |
ожливі |
усилл |
M 0 |
x |
|
||||||||||||||||||||||
кіне атично |
ожливи и пере |
і енн |
и y* |
x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
b |
|
|
d 2 y* x d 2M 0 x |
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
b |
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
* |
|
|
|
|
|
0 |
|
|
|
* |
|
|
|
|
|||||||||||||
|
|
|
M |
|
x |
|
dx2 |
|
|
|
|
dx2 |
|
|
y |
|
x |
dx |
|
|
|
d2M |
|
x |
d1y |
|
x |
a . |
|
(5.57) |
|||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вернувши ува у на |
5.51), фор |
улу (5.57) перепише |
о у ви л ді |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
b |
0 |
|
d |
2 y* x |
|
|
|
|
|
|
|
0 |
|
T |
|
|
* |
|
|
b |
b |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
M |
|
x |
|
|
|
dx |
|
d2M |
|
x |
|
d1y |
|
x |
|
|
y |
|
x q x dx . |
|
|
(5.58) |
||||||||||
|
|
|
|
|
dx2 |
|
|
|
|
|
a |
|
|
|
|
||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При |
виведенні |
|
фор |
|
ули . |
|
|
не |
ули |
|
вра овані |
природні |
|
раничні |
у ови |
5.52 , |
ки |
||||||||||||||||||
адовол н ют |
статично |
ожливі |
усилл |
|
M 0 |
x |
і |
кіне |
атичні |
|
раничні |
у |
ови |
5.54 , |
о |
||||||||||||||||||||
відповідают |
кіне |
атично ожливи |
пере |
і |
енн |
и |
y* |
x . |
|
еінте рал ний член фор |
ули . |
||||||||||||||||||||||||
на підставі |
5.40 |
ожна |
аписати наступни |
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
|
T |
|
|
* |
|
x |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
T |
|
|
|
* |
|
|
x |
|
b |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
d2M |
|
|
|
|
|
d1y |
|
|
|
|
a |
|
|
|
|
I1 I2 d2M |
|
|
|
|
d1y |
|
|
|
|
|
a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
(5.59) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
* |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
I |
|
|
x |
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
I1d2M |
|
|
d1y |
|
|
|
|
|
|
|
|
2d2M |
|
|
|
d1y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
наслідок то о, |
|
о |
|
атриц |
діа онал на, перший доданок у правій частині . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
T |
|
|
|
|
* |
x |
|
b |
|
|
|
|
|
|
|
|
0 |
x |
|
T |
|
|
|
|
|
|
|
* |
|
x |
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
I1d2M |
|
|
|
|
d1y |
|
|
|
|
|
d2M |
|
|
|
I1d1y |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
аки чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
x |
T |
|
|
|
* |
x |
|
b |
|
|
|
|
|
|
|
0 |
|
x |
|
T |
|
|
|
|
|
* |
x |
|
b |
|
|
|
|
|
|
|
|
0 |
|
x |
|
T |
|
|
|
|
|
|
|
* |
x |
|
b |
|
(5.60) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
d2M |
|
|
|
|
d1y |
|
|
|
|
|
|
d2M |
|
|
|
|
I1d1y |
|
|
|
|
|
|
I2d2M |
|
|
|
|
|
|
d1y |
|
|
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
силу |
ранични |
у |
ов |
|
. |
|
, |
|
|
. |
|
|
останн |
рівніст |
на уває ви л ду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
x |
T |
|
|
|
* |
x |
|
b |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
0 |
|
x |
|
b |
|
|
|
|
|
|
T |
|
|
|
* |
|
|
x |
|
b |
|
|
|
|
(5.61) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
d2M |
|
|
|
|
|
|
d1y |
|
|
|
|
|
|
|
|
v x |
|
|
|
d2M |
|
|
|
|
|
p x |
|
|
|
d1y |
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ура уванн |
|
|
|
|
|
. |
|
|
фор |
|
улу |
|
. |
|
|
представи |
|
о наступни |
|
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
b |
0 |
|
d |
2 |
y |
* |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
T |
|
|
|
* |
|
|
|
b |
|
|
b |
* |
|
|
|
|
|
|
|
|||||||||||||||||||
M |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
v x |
|
|
|
d2M |
|
|
x |
|
|
|
p x |
|
d1y |
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
x q x dx. |
(5.62) |
|||||||||||||||||||||||||
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
фор |
улі |
|
|
. |
|
|
|
|
на |
від іну |
|
від . |
|
|
|
|
в |
вно |
у |
ви л ді |
|
присутні |
|
|
раничні |
у ови, |
ки |
|||||||||||||||||||||||||||||||||||||||||||||||
адовол н ют |
статично |
|
ожливі |
|
усилл |
|
M 0 x і кіне атично |
|
ожливі пере |
і |
енн |
y* |
x . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Очевидно, |
|
о дійсні |
усилл |
|
|
M 0 |
|
x і пере і |
|
енн |
|
y0 |
x |
|
адовол н ют |
|
|
інте рал ну тотожніст |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(5.62). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к о скористатис |
|
рівністю 5.55 , |
|
|
|
ка ви начає дефор |
ацію * x , |
відповідну кіне |
атично |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ожливи |
пере |
|
і |
|
|
|
енн |
|
, то співвідношенн |
|
|
. |
|
|
перепишет с |
|
|
у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
b |
|
0 |
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
T * |
|
|
|
b |
|
|
b |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
M |
|
|
|
|
x dx |
|
|
|
v x |
|
|
d2M |
|
|
|
x |
|
|
p x |
|
|
|
|
d1y |
|
x |
|
|
|
|
|
y |
|
|
|
x q x dx. |
|
(5.63) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Енергетичні теореми і варіаційні принципи |
35 |
||||||
а |
е |
а допо о ою фор ул |
. |
а о . |
ожна одержати варіаційні рівн нн а ранжа і |
||
астіл |
но. |
|
|
|
|
|
|
5.6. Варіаційне рівняння Лагранжа |
|
|
|||||
е ай |
y0 x – дійсні пере і |
енн , відповідні крайовій адачі 5.43), (5.44 . Природно, |
о ц |
||||
функці |
|
адовол н є у |
ови ладкості і крайові у |
ови (5.54 . твори о під ножину кіне |
атично |
||
ожливи |
пере і ен |
y* ( x . |
л |
ц о о покладе |
о |
|
|
y* |
x |
y |
0 |
x |
y |
x |
x |
a,b , |
(5.64) |
|
|
|
|
|
|
|
|
|
|
де y x – довіл на варіаці |
пере |
|
і |
енн |
y0 |
x , |
о |
ає неперервну по ідну і |
адовол н є у ови |
I1 d1 y x I1 d1 y x
x |
a |
0, |
(5.65) |
x |
b |
0. |
|
|
|
Величина 0 у правій частині ци співвідношен |
– це дво |
ірний нул овий вектор 0 0 |
0 T. |
|||||||||
ункці |
y x |
на иваєт с |
можливим, |
а о |
віртуальним |
переміщенням. |
силу |
у |
ов, |
|||
накладени |
на нескінченно |
алу функцію |
y x , пере і |
енн |
y* ( x ) також |
ає нео |
|
ідну |
||||
ладкіст |
і |
адовол н є |
раничні у ови . |
, то то дійсно є кіне |
атично ожливи . |
|
|
|
||||
Підставивши |
y* ( x ) |
і M 0 x до . |
і вра овуючи, |
о y0 x і M 0 x адовол н ют |
цю |
|||||||
тотожніст , на підставі . |
отри ає о |
|
|
|
|
|
|
|
||||
|
b |
0 |
d |
2 |
y x |
|
|
T |
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
p x |
d1 y |
y x q |
|
0. |
|
|
|
M |
|
x |
|
dx2 |
dx |
x |
x dx |
(5.66) |
||||
|
a |
|
|
|
|
|
|
a |
a |
|
|
|
|
івніст . |
|
– це інте рал на тотожніст , ка справедлива дл |
уд - ки |
статично |
ожливи |
||||||||
усил |
M 0 x і |
|
ожливи пере і ен y x . |
|
|
|
|
|
|||||
к |
о ввести |
ожливі дефор |
аці |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
d 2 y |
x |
, |
|
|
(5.67) |
|
|
|
|
|
|
|
dx |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
то фор улу . |
ожна переписати наступни чино : |

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
36 |
||||||||||||||
|
|
|
|
b |
|
0 |
|
|
|
|
T |
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
M x x dx p x |
|
d1 y x |
q x |
y x dx 0. |
|
|
|
|
|||||||||||||
|
|
|
|
|
a |
|
|
|
|
||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перший член отри ано о співвідношенн |
– |
це |
ро ота |
статично |
ожливи |
внутрішні |
|||||||||||||||||||
усил |
M 0 |
x на віртуал ни дефор |
аці |
|
x . |
нак |
інус перед інте рало |
по снюєт с ти , |
|||||||||||||||||
о внутрішні |
усилл |
|
діют |
навпроти |
пере |
і ен . |
ру ий |
доданок – |
це |
ро ота |
овнішні |
||||||||||||||
кінцеви |
усил |
p a |
|
i |
p b на відповідни |
віртуал ни |
пере |
і |
енн |
кінців стержн . Останній |
|||||||||||||||
доданок – це ро ота |
овнішн о о ро поділено о навантаженн |
q x |
на віртуал ни |
|
пере |
і енн |
|||||||||||||||||||
осі стержн |
y x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а начи |
о, |
о в дано у випадку |
аєт с |
на ува і не дійсна ро ота, |
ка |
дійснюєт с |
в процесі |
||||||||||||||||||
ро витку дефор |
ацій, а |
ожлива ро ота остаточни |
усил на остаточни |
пере |
і енн . |
|
|
||||||||||||||||||
аки |
|
чино |
, на |
|
|
а і співвідношенн |
|
. |
ожна |
дійти |
до |
висновку |
|
|
|
- |
|||||||||
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
A |
0. |
|
|
|
|
|
|
|
|
|
|
(5.68) |
||
ут U , A– відповідно су и ро іт внутрішні |
і |
овнішні |
сил на |
уд - ки |
|
нескінченно |
|||||||||||||||||||
али |
ожливи |
пере |
|
і |
енн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
фор |
ул оване положенн |
вл є со ою |
основи |
віртуал ни |
пере |
і |
ен |
і |
на иваєт с |
||||||||||||||||
варіаційним рівнянням Лагранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отже, |
варіаційно |
|
у |
рівн нню |
а ранжа |
адовол н є |
уд - |
ке |
статично |
ожливе |
усилл |
||||||||||||||
M 0 |
x . |
Вірни |
є й протилежне твердженн |
к |
о внутрішні |
усилл |
M x |
адовол н ют |
|||||||||||||||||
інте рал ну тотожніст
b |
d |
2 |
y x |
|
T |
b |
b |
|
|
|
|
||||
M |
x |
|
dx2 |
dx p x |
d1 |
y x |
|
a |
|
|
|
|
a a |
||
q x y x dx 0, |
(5.69) |
то усилл M x є статично ожливи и.
ійсно, двічі астосовуючи інте руванн а частина и оже о аписати

5. Енергетичні теореми і варіаційні принципи |
37 |
b |
|
|
|
|
|
d 2 y x |
|
|
|
|
|
|
|
T |
b |
b d 2 M x |
y x dx . |
|
|||||||
|
M x |
|
dx |
2 |
|
dx |
d2 |
M x |
|
d1 y x |
|
|
dx2 |
|
|
||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
||||
Використовуючи ті ж перетворенн , |
о і в співвідношенн |
5.60 , перший доданок ожна |
|||||||||||||||||||||||
представити у фор і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
T |
|
|
|
|
b |
|
|
|
T |
|
|
b |
|
|
|
|
|
T |
|
b |
d2 M x |
|
d1 y x |
a |
d2 |
M x |
|
I1d1 y x |
I2 d2 M x |
d1 |
y x . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
важаючи |
на |
те, |
о |
|
ожливі пере |
і |
енн |
y x |
адовол н ют |
|
у ови |
. |
, останню |
||||||||||||
рівніст ожна переписати наступни |
чино |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
b |
|
|
|
T |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
d2 M x |
d1 y x |
a |
|
I2 d2 M x |
d1 |
y x . |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
||
а підставі |
|
а начено о інте рал на тотожніст . |
на уває ви л ду |
|
|
|
|
||||||||||||||||||
b |
|
d |
2 |
M x |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
b |
|
|
||||
|
|
|
|
dx2 |
|
q x |
y x dx |
|
p x I2 d2 M x |
|
|
d1 |
y x |
0. |
|
||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||
еінте рал ний член у ц о |
у вира і перетвори о а допо о ою |
5.40 |
і . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
T |
|
b |
|
|
|
|
|
T |
|
|
|
|
|
b |
|||
p x I2 d2 M x d1 y x |
|
|
p x I2 d2 M x |
|
|
I1 |
|
I2 d1 y x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
a |
|
b |
|
|
|
|
|
|
T |
|
|
b |
a |
p x I |
2 d2 M x |
|
|
I1 d1 y x |
a |
|
p x I2 d2 |
M x |
|
I2 d1 y x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
T |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||
p x I2 d2 M x I2 d1 y x . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
а підставі отри |
|
ано о ре ул тату |
ожна представити інте рал ну тотожніст |
. |
у ви л ді |
||||||||||||||||||||
b |
d |
2 |
M x |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
b |
|
||||||
|
|
|
|
dx2 |
|
|
q x y x dx p x I2 d2 M x |
|
I2 d1 y x |
0. |
|||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||

5. Енергетичні теореми і варіаційні принципи |
38 |
||||
авд ки довіл ності варіаці |
y x в усі точка |
інтервалу |
a,b , а також довіл ності до утку |
||
I2 δ1 y x на йо о кінц , |
останн о рівності випливає, о |
|
|||
|
|
d 2M |
q x |
0 |
|
|
|
dx2 |
|
||
|
|
|
|
|
|
і
I2 δ2 M x
I2 δ2 M x
x a p a ,
x b p b .
Отже, |
M x є статично |
ожливи |
усилл , то то M x |
M 0 |
x . е свідчит про те, о |
|
інте рал на тотожніст |
. |
, так са |
о к і співвідношенн |
5.51 |
і 5.52 , ви начає статично |
|
ожливі |
усилл . |
|
|
|
|
|
Отже, |
справедливи |
є твердженн |
якщо в будь-якій системі сума робіт усіх внутрішніх і |
|||
зовнішніх сил на будь-яких можливих варіаціях переміщень дорівнює нулю, то система перебуває в стані рівноваги.
к о на підставі 5.43), (5.44 прийн ти
M |
EI |
d 2 y |
(5.70) |
||
dx |
2 |
||||
|
|
|
|||
і підставити до . , то одержи о варіаційне рівн нн |
|
а ранжа |
|||
b |
|
d |
2 |
y d |
2 |
y x |
|
T |
b |
b |
|
|
|
|
|
|
|||||
|
EI |
dx2 |
|
dx2 |
dx p x |
d1 |
y x |
|
||
a |
|
|
|
|
a a |
|||||
q x y x dx 0, |
(5.71) |
де пере і енн y x адовол н є кіне атичні раничні у ови
I1d1y x I1d1y x
xa
xb
v a ,
(5.72)
v b .

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
39 |
|||||||||||||||||||||
івн нн |
|
. |
|
на иваєт с |
варіаційни |
|
рівн нн |
а ранжа, аписани |
відносно кіне |
атично |
|||||||||||||||||||||
ожливи пере і ен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Варіаційно о рівн нн |
а ранжа в фор |
|
і . |
|
недостатн о дл |
повно о ви наченн ро в' ку |
|||||||||||||||||||||||||
адачі і отри |
анн |
дійсни |
усил |
M 0 |
x , |
|
дефор |
ацій 0 x |
і пере і |
ен |
y0 |
x , оскіл ки під |
|||||||||||||||||||
час фор |
улюванн |
рівн нн не використовувавс |
фі ичний |
акон M |
EI див.5.43 . Але післ |
||||||||||||||||||||||||||
використанн |
|
. |
|
принцип |
ожливи |
|
пере і |
ен , а о варіаційне рівн нн |
|
а ранжа в фор і |
|||||||||||||||||||||
(5.71 |
вже до вол є |
кіне |
атично |
ожливи |
|
пере |
і |
ен |
y * (x) виділити дійсні y0 |
x . |
ійсно, |
||||||||||||||||||||
. |
і . |
|
випливає, |
|
о функці |
EI |
|
d 2 y |
|
статично |
ожлива, то то адовол н є рівн нн |
||||||||||||||||||||
|
|
|
dx2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рівнова и |
5.51 |
і |
раничні у ови (5.52 . |
|
к |
о до то о ж поставити ви |
о у, |
о |
пере |
і |
енн |
||||||||||||||||||||
y x |
|
y* |
x |
|
ули |
кіне |
атично |
ожливи |
и, |
то |
ро в' |
ок |
рівн нн |
. |
|
|
уде |
адовол н ти |
|||||||||||||
рівн нн |
5.47), (5.48 . |
а цій підставі |
ожна вважати, |
о варіаційне рівн нн |
а ранжа в фор і |
||||||||||||||||||||||||||
. |
є варіаційною постановкою |
адачі, |
|
і ц |
постановка ви начає єдиний ро в' |
ок на класі |
|||||||||||||||||||||||||
кіне |
атично |
ожливи пере і ен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
аведена варіаційна постановка адачі припускає пере ід до еквівалентно |
варіаційно |
адачі в |
||||||||||||||||||||||||||||
фор |
і у |
ови стаціонарності функціоналу на класі кіне атично |
ожливи |
пере |
і |
ен . |
|
|
|||||||||||||||||||||||
|
ідно |
|
фор |
улою 5.8 і співвідношенн |
|
5.56 , потенціал на енер і |
дефор аці |
ину |
|||||||||||||||||||||||
стержн |
дл |
де ко о кіне |
атично |
ожливо о пере |
і |
енн |
y* |
x |
ає ви л д |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
U |
|
1 |
b EI * x 2 dx , |
|
|
|
|
|
|
|
|
|
(5.73) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де дефор |
аці |
* |
x |
пов' |
ана |
кіне атично |
|
ожливи |
и |
пере і |
енн |
и |
співвідношенн |
||||||||||||||||||
(5.55 . Отже, |
варіаці |
потенціал но енер і |
|
дефор |
аці , |
о у |
овлена y* |
x , |
оже |
ути |
аписна |
||||||||||||||||||||
наступни |
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
EI * |
|
x * |
x dx . |
|
|
|
|
|
|
|
|
|
(5.74) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ура уванн |
|
співвідношен |
5.35 |
|
і |
5.67 |
|
варіаці |
потенціал но енер і |
представл єт с |
||||||||||||||||||||
фор |
улою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
b |
d 2 y* x d 2 y* x |
dx . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
EI |
|
|
|
dx2 |
|
|
dx2 |
|
|
|
|
|
|
|
(5.75) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
40 |
||||||||||||||||||||
відси випливає дру а фор |
а варіаційно о рівн нн |
а ранжа . |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
* |
|
b |
b |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
U |
p x |
d1 y |
|
x |
a |
|
q |
|
x y |
|
x dx , |
|
(5.76) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ке ви начена на кіне |
атично |
ожливи |
пере і |
енн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вра овуючи те, |
о |
овнішні |
сили не варіюют с , |
|
операцію варіюванн |
ожна винести і |
||||||||||||||||||||||
отри ати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
(5.77) |
||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
* |
|
|
|
T |
|
|
* |
|
b |
|
b |
|
* |
|
|
|
|
|
|
|
|
|
|
1 y |
U y |
|
|
|
x |
|
|
y |
x q x dx. |
(5.78) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
p x |
|
d1y |
|
|
a |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ункціонал |
1 y* |
на иваєт с |
функціоналом |
Лагранжа, |
а о |
функціоналом |
повної |
|||||||||||||||||||||
потенціальної енергії. |
Він дорівнює рі ниці потенціал но енер і |
|
дефор ацій дл y* і ро оти |
|||||||||||||||||||||||||
адани |
овнішні |
сил, |
кі не |
|
інюют с |
в процесі |
|
іни пере |
|
і |
ен y*. ункціонал |
а ранжа |
||||||||||||||||
ро л даєт с |
на кіне |
атично |
|
ожливи |
пере |
і |
енн |
. |
|
|
івніст |
|
|
. |
|
є умовою стаціонарності |
||||||||||||
функціоналу Лагранжа, вона еквівалентна варіаційно у рівн нню |
5.71 . аки |
чино , |
||||||||||||||||||||||||||
пере і |
енн |
y*, |
ке |
|
надає |
функціоналу . |
|
стаціонарне |
наченн , |
адовол н є варіаційне |
||||||||||||||||||
рівн нн |
|
. |
і, отже, є дійсни |
. |
а |
підставі |
а начено о |
|
|
ожна |
сфор |
улювати |
принцип |
|||||||||||||||
стаціонарності повно |
потенціал но |
енер і |
|
серед усіх кінематично можливих переміщень |
||||||||||||||||||||||||
дійсні переміщення надають повній потенціальній енергії стаціонарне значення.
Постановка |
адачі . |
, . |
також є варіаційною. |
л не |
|
рівн нн |
5.47 |
є рівн нн |
|||
Ейлера. відси випливают |
природні природні |
раничні у |
ови. |
|
а о |
у |
ова и |
5.54 , ки |
|||
кіне атично |
ожливі пере |
і енн |
адовол н ют |
а ви наченн |
, |
рівн нн |
Ейлера і природні |
||||
раничні у ови варіаційно |
адачі . |
, . |
повністю ви начают |
|
крайову |
адачу 5.47), (5.48). |
|||||
сі три постановки у ви л ді крайово |
адачі дл диференціал но о рівн нн |
. , . |
|||||||||
варіаційне рівн нн а ранжа . |
і стаціонарності функціоналу |
. |
, . |
|
є еквівалентни и. |
||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
41 |
|||||||||||||||||||
5.7. Варіаційне рівняння Кастільяно |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
е ай |
M 0 x |
– |
дійсні |
усилл , |
відповідні крайовій |
адачі |
5.44), (5.45 . |
Природно, |
о ці |
|||||||||||||||||
усилл |
адовол н ют |
рівн нн |
|
(5.51 і природні крайові у ови (5.52 . |
твори о під ножину |
|||||||||||||||||||||
статично |
ожливи |
усил M 0 x |
|
|
а допо |
о ою співвідношенн |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
M 0 |
x |
|
M |
0 |
|
x |
M |
x |
|
x |
a,b , |
|
|
|
|
(5.79) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де M |
x |
– довіл на варіаці |
|
|
|
усилл |
M 0 |
x , ка |
адовол н є однорідне диференціал не |
|||||||||||||||||
рівн нн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 M |
x |
0 |
|
|
|
|
|
|
|
(5.80) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
і однорідні природні крайові у ови |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
I2d2 M |
x |
x |
a |
0, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.81) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
I2d2 M |
x |
x |
b |
0, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де 0T |
0 |
0 – нул овий вектор. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ункці |
M |
x на иваєт с |
|
статично |
ожливою варіацією |
усилл |
M 0 x . Внаслідок у |
ов, |
||||||||||||||||||
о накладают с |
на нескінченно |
|
|
алу функцію M x , усилл |
M 0 |
x |
адовол н є рівн нн |
|||||||||||||||||||
(5.51) і природн |
раничн у |
ови (5.52), то то дійсно є статично |
ожливи . |
|
|
|
||||||||||||||||||||
Підставивши |
y* |
x |
і M 0 x |
|
|
до (5.62) і вра овуючи, |
о y* |
x |
і M |
0 |
x |
адовол н ют |
цю |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тотожніст , на підставі (5.80) і (5.81) отри ає |
о |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
b |
|
d |
2 |
|
y |
* |
x |
|
|
|
|
T |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
v x |
|
d2 M |
|
|
0. |
|
|
|
||
|
|
|
|
|
x |
|
|
|
dx2 |
dx |
|
|
x |
|
|
(5.82) |
||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||
івніст |
(5.82) становит інте рал ну тотожніст , |
ка виконуєт с |
дл |
кіне атично ожливи |
|
пере і ен |
y* x і статично ожливи варіаці |
усил M x . |
івн нн (5.82) носит |
на ву |
|
варіаційного рівняння Кастільяно. Воно є дво сти |
анало о рівн нн |
а ранжа (5.66) |
у то у |
||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
42 |
||||||||||||||||||||||||||||
сенсі, |
о |
к |
о рівн нн |
|
а ранжа виражає основні співвідношенн |
іж нескінченно |
али |
и |
|||||||||||||||||||||||||||||
кіне |
атично |
ожливи |
и варіаці |
|
|
|
и пере і |
ен |
і статично |
ожливи |
и |
усилл |
и, то рівн нн |
||||||||||||||||||||||||
астіл |
но ви начає |
|
|
в' |
ок |
іж нескінченно |
али |
и статично |
ожливи и варіаці |
и внутрішні |
|||||||||||||||||||||||||||
усил |
і кіне атично |
|
|
|
ожливи |
и пере |
|
і |
енн |
и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
а підставі варіаційно о рівн нн |
|
астіл |
но (5.82) |
|
ожна дійти до висновку |
|
|
|
|||||||||||||||||||||||||||||
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Це положення носить назву |
|
|
|
|
|
|
||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, варіаційно у рівн нню |
|
астіл |
но |
адовол н ют |
уд - кі |
кіне атично ожливі |
|||||||||||||||||||||||||||||||
пере і енн . Вірни |
|
|
|
є і |
воротне твердженн |
к |
о де ка функці |
y x |
адовол н є варіаційнк |
||||||||||||||||||||||||||||
рівн нн |
|
астіл |
|
|
но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
b |
M |
|
d |
2 |
y x |
|
|
|
|
|
T |
|
|
M |
|
b |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
dx |
x |
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
v |
|
|
d2 |
|
|
0, |
|
|
|
(5.83) |
|||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||
то вона є кіне |
атично |
|
ожливи |
пере |
|
і |
енн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Оскіл ки варіаці |
M x |
пов' |
|
|
ані співвідношенн |
|
|
и . |
|
, . |
|
і, отже, не є довіл ни |
и, до |
||||||||||||||||||||||||
ни |
оже |
ути |
|
|
астосований |
етод неви начени |
ножників |
а ранжа. Введе |
о в інтервалі |
a,b |
|||||||||||||||||||||||||||
де ку функцію x |
, по |
ножи о |
|
|
на рівн нн |
(5.83) і |
апише |
о ре ул тат у ви л ді |
|
|
|||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
d y |
x |
|
|
|
|
|
d M |
x |
|
|
|
|
|
T |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
a |
|
M |
|
x |
|
dx2 |
|
|
|
x |
|
|
dx2 |
|
dx |
|
|
|
v |
x |
|
d2 M |
x |
a |
0. |
|
(5.84) |
|||||||||
|
рівн нні (5.84) на від |
іну від (5.82) фі урує не |
y* |
x , а |
y x , оскіл ки |
е слід довести, |
о |
||||||||||||||||||||||||||||||
y x |
– |
це кіне |
|
атично |
ожливі пере і |
енн , |
кі підпор дковуют с |
ранични |
у ова |
(5.54). |
|||||||||||||||||||||||||||
користавшис фор улою (5.50) |
|
|
дійсні |
о де кі перетворенн |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
b |
|
|
|
d 2 M x |
|
|
|
|
|
b |
|
|
|
d 2 |
x |
|
|
|
|
|
|
|
T |
|
|
b |
|
|
||||||
|
|
|
|
x |
|
|
|
dx2 |
dx |
|
|
|
M |
x |
dx2 |
|
dx |
d2 M |
x |
|
d1 x . |
(5.85) |
|||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
||||||
Анало ічно перетвори о неінте рал ний член у рівн нні (5.85):

5. Енергетичні теореми і варіаційні принципи |
43 |
|
|
|
|
|
|
|
T |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
b |
|
|
|
||||
|
|
|
|
d2 M x |
|
d1 x |
a |
|
|
I1 |
|
I2 d2 M x |
d1 |
|
x |
a |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
T |
|
|
b |
|
|
|
|
|
|
|
T |
|
|
b |
|
|
|
|
|
|||||||||
|
|
|
|
I1d2 M x |
|
|
d1 x |
a |
|
I |
2d2 |
M x |
|
d1 x |
a |
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а підставі (5.81) |
ає о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
b |
|
|
|
|
|
|
T |
|
|
|
b |
|
|
|
|
|
|
|
||||
|
|
|
|
d2 |
M x |
|
d1 x |
a |
|
|
I1d2 |
M x |
|
d1 |
x |
a |
|
|
|
|
|
|
(5.86) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
I1d2 M x |
|
I1 d1 |
x |
a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ура уванн |
|
дво |
останні |
співвідношен |
(5.85) і (5.86) представи |
о рівн нн |
(5.84) у фор і |
|||||||||||||||||||||||||||||
b |
|
d |
2 |
y x |
d |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
b |
|
|
|
a M |
x |
|
dx2 |
|
dx2 |
|
|
|
dx . |
|
I1d2 M |
x |
|
v |
x |
I1d1 |
|
x |
|
a |
0. |
(5.87) |
||||||||||||||
При отри анні рівн нн . |
|
|
|
ули |
е ра |
використані у |
ови |
5.81). |
|
|
|
|
|
|
|
|
||||||||||||||||||||
астосуванн |
|
ножника |
|
а ранжа x |
|
до вол є вважати функцію M |
|
|
x |
у рівн нні . |
||||||||||||||||||||||||||
довіл ною в усі точка інтервалу |
a,b . о то о ж вектор I1d2 M |
x |
|
є довіл ни на кінц |
||||||||||||||||||||||||||||||||
інтервалу. |
а а і основно ле и варіаційно о численн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d 2 y x |
|
d |
2 x |
x |
a,b . |
|
|
|
|
|
|
|
|
|
(5.88) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
овіл ніст |
вектора I1d2 M x |
|
на кінц |
|
інтервалу до вол є |
аписати рівності |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
I1d1 a |
|
v |
|
|
a , |
|
|
|
|
|
|
|
|
|
|
|
|
(5.89) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
I1d1 b |
|
v |
|
|
b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
співвідношенн |
(5.88) |
ожна по ачити, |
о x |
|
ожна ототожнити |
|
|
пере |
і енн |
y x . |
||||||||||||||||||||||||||
оді рівності (5.89) до вол ют |
|
стверджувати, |
о пере і |
енн |
є кіне |
атично |
ожливи |
и, то то |
||||||||||||||||||||||||||||
y x |
y* |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, |
ожна сфор улювати наступне |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Використовуючи рівності (5.43) встанови |
о |
в' |
|
ок |
іж пере |
і |
енн |
|
и і |
|
усилл |
и |
|
|||||||||||||||||||||||

5. Енергетичні теореми і варіаційні принципи |
44 |
|
|
|
|
d 2 y |
|
M |
. |
|
|
(5.90) |
|
|
|
|
dx2 |
EI |
|
|
|||
|
|
|
|
|
|
|
|
|||
Підставивши (5.90) до (5.82) отри |
ає |
о варіаційне рівн нн |
|
|
||||||
b M x M |
x |
|
|
T |
|
b |
|
|||
|
M x |
0. |
(5.91) |
|||||||
|
EI |
|
dx v x |
d2 |
||||||
a |
|
|
|
|
|
|
|
a |
|
|
е рівн нн на иваєт с варіаційним рівнянням Кастільяно, записаним відносно статично
можливих зусиль.
Використовуючи ножник а ранжа пока ати, о
x так са о, к це уло ро лено раніше, ожна
|
|
|
|
|
|
|
|
|
d 2 |
|
M |
|
|
|
|
|
|
|
|
|
|
|
(5.92) |
|||
|
|
|
|
|
|
|
|
|
dx2 |
|
EI |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1d1 a |
|
v a , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
I d b |
v b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к о ототожнити |
|
ножник |
|
а ранжа |
x |
кіне |
атично |
ожливи |
и |
пере і |
енн |
и |
|||||||||||||
y* x , то |
' суєт с , |
|
о |
усилл |
|
M x , |
ке |
адовол н є у |
ови рівнова и |
M x |
|
M 0 |
x |
, |
||||||||||||
пов' |
ані |
рівн нн |
|
(5.92), ке вра овує фі ичний |
акон. Отже, |
M 0 x |
і |
y* |
x |
адовол н ют |
|
|||||||||||||||
рівн нн (5.45) і раничні у |
ови (5.46), то то вони є дійсни |
и. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Анало ічно то |
у, |
к це |
уло ска ано |
приводу варіаційно о рівн нн |
|
а ранжа у фор |
і (5.66), |
|||||||||||||||||||
тут також |
ожна стверджувати, |
о варіаційно о рівн нн |
астіл |
но у фор і (5.82) недостатн о |
||||||||||||||||||||||
дл повно о ви наченн |
ро в' |
ку |
адачі і отри |
анн |
дійсни |
усил |
M 0 |
x , дефор ацій 0 |
x |
і |
||||||||||||||||
пере |
і ен |
y0 x , оскіл ки при |
|
апису рівн нн |
(5.82) не |
ув використаний фі ичний |
акон. |
|||||||||||||||||||
авд ки ура уванню (5.90), |
принцип ожливи |
напружен , а о варіаційне рівн нн |
астіл |
но в |
||||||||||||||||||||||
фор |
і (5.91) до вол є виділити |
класу статично |
ожливи |
усил |
M 0 x дійсні |
усилл |
M |
0 |
x . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аки |
чино , варіаційне |
рівн нн |
астіл |
но в |
фор і |
(5.91) |
– |
це |
|
ате |
атична |
варіаційна |
||||||||||||||
постановка |
адачі, |
о |
водит |
до |
єдино о |
ро в' |
ку на класі статично |
ожливи |
внутрішні |
|
||||||||||||||||
усил . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
45 |
|||||||
Відповідно |
до (5.43) потенціал ну енер ію |
дефор аці дл де ко о статично |
ожливо о |
|||||
вектора усил |
M 0 x |
ожна аписати у ви л ді |
|
|
|
|||
|
|
U |
1 b |
M 0 x |
2 |
dx. |
(5.93) |
|
|
|
2 |
a |
EI |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Варіаці ціє |
енер і |
представл єт с співвідношенн |
|
|||||
|
|
U |
b M 0 x M 0 |
x |
dx. |
|
|
|
|
|||
|
|
|
|
EI |
|
|
|
|
|
|||
|
|
|
|
a |
|
|
|
|
|
|
|
|
оді варіаційне рівн нн |
астіл |
но (5.91) |
ожна представити у фор і |
|||||||||
|
|
|
|
|
|
T |
|
b |
|
|
|
|
|
|
U |
v a |
|
d2 M |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
Введе |
о функціонал Кастільяно: |
|
|
|
|
|
|
|
|
|||
|
П2 M |
0 |
U M |
0 |
v x |
T |
0 |
x |
|
b |
||
|
|
|||||||||||
|
|
. |
||||||||||
|
|
|
|
d2M |
|
|
||||||
|
|
|
v a |
i v b |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||
адані кінцеві пере і енн |
|
не варіюют с , то у операцію варіюванн |
||||||||||
винести а |
нак функціоналу і отри ати в силу (5.95) |
|
|
|
|
|
|
|||||
(5.94)
(5.95)
(5.96)
ожна
|
|
|
|
|
|
|
|
|
2 |
0 . |
|
|
|
|
|
|
|
(5.97) |
|
ункціонал |
астіл |
но |
. |
на иваєт с |
також функціонало |
додатково енер і , |
ка і |
||||||||||||
воротни |
нако |
дорівнює рі ниці потенціал но |
енер і |
дефор |
аці |
дл |
статично |
ожливи |
|||||||||||
усил M 0 x |
і ро оти кінцеви |
усил |
та |
, де |
адано кінцеві пере і |
енн . Вважаєт с , |
о в |
||||||||||||
процесі дефор |
аці |
кінцеві |
усилл |
не |
|
інюют с . |
ункціонал |
|
астіл |
но ро л даєт с |
на класі |
||||||||
статично |
ожливи |
усил |
M 0 x . |
івн нн |
|
. |
– це у |
ова стаціонарності додатково енер і . |
|||||||||||
татично |
ожливі |
усилл |
M 0 x , |
о надают |
функціоналу |
2 |
M 0 |
стаціонарне |
наченн , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
адовол н ют |
рівн нн |
. |
, а о |
|
. |
, і, |
отже, є дійсни |
и. |
а начене до вол є сфор |
улювати |
|||||||||
.
5. Енергетичні теореми і варіаційні принципи |
46 |
адача |
. , |
. , |
к і |
пов' уют внутрішні усилл |
|||
пере і енн |
є |
ожливи |
и. |
адача . |
, |
є варіаційною. |
івн нн |
Ейлера |
дл |
тако |
адачі |
||
пере |
і енн |
|
и, а природні раничні у |
ови а е печуют те, |
о ці |
||||
аки |
чино |
, |
ра о |
рівн нн |
и рівнова и, |
ки |
адовол н є |
||
M 0 x , рівн нн |
Ейлера і природні раничні у |
ови утворюют крайову |
адачу 5.45), (5.46). |
|||
Все а начене |
ожна ре ю увати наступни |
чино |
крайова |
адача |
. , . , варіаційне |
|
рівн нн . |
і у |
ови стаціонарності функціоналу . |
вл ют |
со ою еквівалентні постановки |
||
адачі про |
ин стержн . |
|
|
|
|
|
5.8. Екстремальні властивості функціоналів Лагранжа і Кастільяно
к |
уло |
а начено |
ви |
е, дійсні пере і |
енн y0 x |
і дійсні |
усилл |
M 0 |
x надают |
||||||||||
стаціонарні |
наченн |
функціоналу повно |
енер і |
1 y і функціоналу додатково |
енер і |
2 M |
|||||||||||||
відповідно. |
о |
л не |
о питанн |
чи |
удут |
ці стаціонарні наченн |
екстре |
у |
а и і, |
к |
о так, то |
||||||||
ки и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
початку |
о числи о |
стаціонарне |
наченн |
функціоналів |
а ранжа |
|
1 y і |
|
астіл но |
||||||||||
2 M . |
л |
ц о о |
скористає |
ос |
теоре |
ою |
лапейрона |
див. |
п. . |
, |
ідно |
ко |
фактично |
||||||
витрачена |
на |
дефор |
уванн |
дійсна ро ота статично прикладени |
овнішні |
сил |
дорівнює |
||||||||||||
половині до утку кінцеви |
начен |
ци |
сил на відповідні пере і |
енн . |
к |
о |
ожлива ро ота |
||||||||||||
оже |
ути |
аписана у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
T |
|
T |
|
b |
b |
|
|
|||||
A v x d2M 0 |
x p x d1y0 |
x |
|
|||
a |
|
|||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
q x y0 x dx , |
(5.98) |
то дійсна ро ота становити е
|
|
|
1 |
|
|
|
1 |
T |
|
|
|
|
|
|
T |
|
|
|
|
b |
1 b |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A0 |
|
A |
|
|
|
v x |
d2M0 x |
|
|
|
p x |
d1y0 |
x |
|
|
|
|
q x y0 x dx. |
(5.99) |
||||||||
2 |
2 |
|
|
|
|
|
a |
2 |
a |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Внаслідок то о, |
о потенціал на енер і |
дефор |
аці |
U0 дорівнює половині ожливо |
ро оти |
||||||||||||||||||||||
овнішні сил, ає о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 b |
|
|
|
d 2 y0 x |
2 |
|
|
1 b M 02 x |
|
|
|
|
|
|
|
|
|
||||||
U0 |
|
EI |
dx |
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
a |
dx |
2 |
|
2 |
|
|
EI |
|
|
|
|
|
|
|
(5.100) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
||||
1 |
|
|
T |
|
|
|
|
T |
|
b |
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
v x d2M 0 x |
p x d1 y0 |
x |
|
|
|
q x y0 x dx. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
a |
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
47 |
|||||||||||||||||||||||||||||||||
авд ки 5.78 |
|
|
і . |
|
стаціонарне |
наченн |
функціоналу |
а ранжа, |
о відповідає дійсни |
||||||||||||||||||||||||||||||||||||
наченн |
y0 x |
і M 0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
b |
1 |
|
|
|
|
T |
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1 w0 |
|
|
|
|
|
v x |
|
d2 M0 x |
|
|
|
|
p x |
|
|
d1 y0 |
x |
|
|
|
|
q x y0 x dx |
0. |
(5.101) |
|||||||||||||||||||
|
|
2 |
|
|
a |
2 |
|
|
a |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Анало ічно, ви од чи |
|
|
|
. |
|
, |
ожна |
отри |
|
ати, |
о |
|
стаціонарне |
наченн функціоналу |
|||||||||||||||||||||||||||||||
астіл |
но також дорівнює |
|
0 , то то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y0 |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.102) |
|||||||
Отже, |
ає о, |
|
|
|
|
|
о |
|
стаціонарні наченн |
|
|
|
функціоналу |
а ранжа |
і функціоналу |
астіл |
но |
||||||||||||||||||||||||||||
і ают с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 y0 |
|
|
|
2 M0 |
|
|
|
|
0 . |
|
|
|
|
|
|
|
(5.103) |
|||||||||||
адалі нео |
ідно |
|
дослідити |
поведінку |
ци |
|
функціоналів |
в околі дійсно о |
напружено- |
||||||||||||||||||||||||||||||||||||
дефор |
овано о стану. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Почне |
о дослідженн |
|
функціоналу |
|
|
а ранжа. |
О числи о рі ницю |
1 y* |
|
0 , |
де, |
к і |
|||||||||||||||||||||||||||||||||
раніше, |
y* x – кіне |
атично |
ожливі пере |
|
і |
енн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
П y* |
|
П |
0 |
|
П y* |
|
П |
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
b |
|
|
d |
2 |
y |
* |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
* |
|
|
b |
|
|
|
|
* |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
dx |
|
|
|
p x |
|
d1y |
|
x |
|
|
|
|
|
q x y |
|
x dx |
|
|
|
|
|||||||||
|
|
|
2 |
|
|
a |
|
dx2 |
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
b |
|
|
d |
2 |
y0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
dx |
|
|
|
p x |
|
d1y0 x |
|
|
|
|
|
q x y0 |
x dx |
|
|
(5.104) |
|||||||||||||
|
|
|
2 |
|
|
a |
|
dx2 |
|
2 |
|
|
|
|
|
|
2a |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 b |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 y0 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 b |
|
|
d 2 y* |
x |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
EI |
|
|
|
|
dx |
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
a |
|
dx2 |
|
|
|
|
2 |
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
T |
|
|
|
|
* |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
p x |
|
d1y0 x d1y x |
|
|
|
|
q x y0 |
|
|
x |
y x dx. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Використовуючи |
фор |
улу |
|
ріна |
і |
прийн вши |
f |
x |
|
|
M 0 x |
|
i |
g x |
y* |
x |
y0 |
x , |
|||||||||||||||||||||||||||
о числи |
о інте рал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
48 |
||||||||||||||||||||||||
b |
|
|
|
d |
2 y* x |
|
d |
2 y0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M |
0 |
x |
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
dx2 |
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.105) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
b d 2M 0 x |
|
|
|
||||||
|
|
|
|
|
|
|
T |
|
|
* |
|
|
|
|
|
|
|
|
* |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
d2M 0 |
|
x |
d1 |
y |
|
|
x y x |
|
|
|
|
|
y |
|
x y0 |
x dx |
||||||||||||
|
|
|
a |
a |
dx2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вра овуючи, |
о |
M 0 |
x – |
дійсні усилл , рівніст |
|
. |
|
ожна переписати наступни |
|||||||||||||||||||||
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
d 2 y* |
|
x |
|
|
d 2 y0 x |
|
|
|
|
|
|
|
|
||||||||
|
|
M 0 |
x |
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||||||||
|
a |
|
|
dx2 |
|
|
|
|
dx2 |
|
|
|
|
|
(5.106) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
|
|
||||||
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
p x d1 y x y0 |
|
x |
q x y x y0 x dx |
|
|||||||||||||||||||||||
|
|
|
a |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Підстави о . |
|
|
у . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
w |
|
|
|
1 b |
EI |
|
d |
2w (x) |
dx |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
0 |
|
2 |
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 b |
d 2w |
(x) |
|
|
|
|
|
b |
|
|
|
|
d 2w (x) |
d |
2w |
(x) |
|
|
|
|
||||||
|
|
|
|
|
|
EI |
0 |
|
|
|
|
|
|
dx |
|
|
M0 (x) |
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
dx2 |
|
|
|
|
|
|
|
dx2 |
|
dx2 |
|
|
|
|
||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 b |
|
d 2w (x) |
d 2w |
|
(x) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
dx. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
dx2 |
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, |
ожна |
аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 y* |
|
|
|
|
0 |
|
1 y* |
1 y0 |
0, |
|
|
|
|
|
(5.107) |
||||||||
причо |
у |
нак рівності справедливий лише |
|
|
а у |
|
ови, |
|
о y* |
x |
y0 |
x . |
|
|
|
|
|
||||||||||||||
о |
л не о тепер функціонал |
астіл |
|
но. О числи о рі ницю |
0 |
2 M 0 , де |
M 0 x – |
||||||||||||||||||||||||
статично |
ожливі усилл . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
2 M 0 |
|
2 M0 |
|
|
|
|
|
2 M 0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
b |
|
|
2 |
|
|
|
|
b |
|
|
|
0 |
|
|
2 |
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
1 M0 x |
|
1 M |
x |
|
|
|
|
|
|
|
0 |
|
b |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
v x |
d2 |
M |
0 x |
M |
|
x |
. |
(5.108) |
|
|
2 |
|
|
EI |
|
2 |
|
|
|
|
|
EI |
|
|
|
|
||||||||||||||
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
49 |
||||||||||||||||||||||||
Прийн вши f x |
|
|
M 0 |
x |
|
M 0 |
x |
|
і |
g x |
y0 x |
і вра овуючи співвідношенн |
. , |
|||||||||||||||||
використає |
о фор улу |
ріна |
5.50 |
|
дл |
о численн інте ралу |
|
|
|
|
|
|
||||||||||||||||||
|
b |
M 0 |
x |
|
M |
0 |
x |
|
d |
2 |
y0 |
x |
|
|
v x |
T |
|
0 |
|
|
b |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
d2 M 0 |
x M |
|
x |
. |
(5.109) |
||||||||||
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Підставивши співвідношенн |
|
. |
|
|
до рівн нн |
. |
|
|
отри ає |
о |
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
1 b M |
0 x |
2 |
|
|
|
|
1 b M 0 x 2 |
|
b |
|
0 |
|
d 2 y0 x |
|
||||||||||||
0 |
2 M |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
dx M0 |
x M |
|
x |
|
|
dx. |
||
|
2 |
|
|
|
EI |
|
|
|
2 |
|
|
EI |
|
|
|
|
dx2 |
|||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||||
Перепише о цей ре ул тат |
|
ура уванн |
|
|
|
рівн н |
5.45) |
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
2 M |
0 |
|
|
1 b |
M0 |
x 2 |
|
dx |
|
1 b M 0 x |
2 |
dx |
|
|
||||||||||
|
|
|
|
2 |
a |
|
EI |
|
|
2 |
|
a |
|
EI |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
b M0 x M 0 x M0 x |
dx |
|
|
1 b |
M0 x M 0 x |
dx. |
|||||||||||||||||||
|
a |
|
|
EI |
|
|
|
|
|
|
2 |
a |
|
|
|
|
|
|
EI |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, |
ає о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 M 0 |
2 M0 |
|
|
|
2 M 0 0 , |
|
|
||||||||||||||
причо у |
нак рівності справедливий лише |
а у |
ови M 0 |
x |
|
|
M0 x . |
|
|
|
|
|||||||||||||||
піввідношенн . |
і . |
|
до вол ют |
аписати послідовніст |
нерівностей |
|||||||||||||||||||||
|
|
1 y* |
|
1 y0 |
0 |
|
0 M0 |
|
|
0 M 0 . |
|
|
||||||||||||||
аки |
чино , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
1 |
|
y* |
1 |
|
y |
0 |
|
|
п |
|
; |
|
|
|
|
|||||||
|
|
|
y* |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
max |
2 |
M 0 |
|
2 |
|
M |
0 |
|
|
|
п . |
|
|
|
|
||||||||
|
|
|
M 0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(5.110)
(5.111)
(5.112)
аведені співвідношенн довод т , |
о стаціонарні наченн функціоналу а ранжа становл т |
іні у , а функціоналу астіл но – |
акси у . |
Отже, сфор улює о два принципи |
|

5. Енергетичні теореми і варіаційні принципи |
50 |
1.
2. |
|
|
|
|
|
|
|
ункціонал |
а ранжа є випукли |
уни , а функціонал |
астіл но – випукли |
увер . |
|
||
о л не |
о |
астосуванн |
варіаційно о під оду на |
прикладі конкретно |
адачі про |
ин |
|
пр олінійно |
|
алки постійно |
о перері у, ка ає на ліво |
у кінці шарнірну опору, а на право |
у |
||
атисненн . |
а право у кінці |
алки |
адано кут повороту 0 рис. . . |
|
|
||
ис. .12 райова адача 5.44), (5.45 у дано у випадку аписуєт с у ви л ді
|
|
|
|
|
|
|
d 2M |
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.113) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
d 2w |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
dx2 |
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
I1d1w x I2d |
2M x |
|
x 0 |
v 0 p 0 , |
|
|
(5.114) |
|||||||||||||||||||
|
|
|
w x I |
|
|
|
M x |
|
|
|
|
v l |
p l , |
|
|
|
|||||||||||
|
I d |
2 |
d |
2 |
|
x |
l |
|
|
|
|
||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де при x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
1 |
|
|
0 |
, I2 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|||||
0 |
|
|
0 |
|
|
|
0 |
|
|
|
1 |
|
, v 0 |
0 |
, p 0 |
0 |
; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
при x l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
1 |
0 |
|
|
I2 |
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
||||||
0 |
1 |
, |
|
|
0 |
|
|
0 |
, |
|
|
v l |
|
|
, |
p l |
|
0 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||||
Ви начи о про ин |
алки, |
ви од чи |
|
|
функціоналу |
а ранжа |
5.58 |
ура уванн то о, о |
|||||||||||||||||||
овнішнє навантаженн |
q x |
|
|
0. |
о у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 w* |
|
|
|
1 l |
EI |
|
d 2w* x |
2 dx. |
|
|
|
(5.115) |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
dx2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Енергетичні теореми і варіаційні принципи |
|
|
51 |
|||||
ункціонал . |
ро л даєт с |
на |
ножині кіне |
атично ожливи пере і |
ен |
w* |
x , о |
|
складаєт с |
функцій, |
кі не порушуют |
суціл ніст |
алки і адовол н ют кіне |
атичні |
раничні |
||
у ови. дано |
у випадку кіне атичні |
раничні у ови ви начают с співвідношенн |
и |
|
||||
|
|
|
w* 0 w* l |
0, |
|
|
(5.116) |
|
|
|
|
|
|
|
dw |
|
|
0 . |
|
|
|
|
|
|
|
|
(5.117) |
||
|
|
|
|
|
|
dx x l |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Шукати е о |
іні |
у |
функціоналу . |
|
на |
однопара |
етричній |
під |
ножині |
кіне |
атично |
||||||||
ожливи пере |
і ен , |
ка ви начаєт с |
наступни |
чино . |
|
|
|
|
|
|
||||||||||
|
о л не о функцію |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
x3 |
|
x2 |
, |
|
|
|
|
|
(5.118) |
||
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
l |
|
|
|
|
|
|
|
ка |
адовол н є |
раничні у |
ови . |
, у ові |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
d x |
|
|
1, |
|
|
|
|
|
|
(5.119) |
||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
l |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а також функці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
x |
1 |
x |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
адовол н є |
раничні у |
ови (5.116) та у |
ову |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
d 1 |
x |
|
|
|
0. |
|
|
|
|
|
|
(5.120) |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x l |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Однопара етрична |
під |
ножина |
ви начаєт с , |
ви од чи |
функцій |
x |
і 1 |
x , а |
|||||||||||
допо о ою пара |
етру w |
співвідношенн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
w 1 x |
|
|
|
|
wx |
|
x |
2 |
x3 |
x2 |
|
|
|
|||
|
w* x |
|
0 x |
|
1 |
l |
|
|
0 l2 |
l . |
|
(5.121) |
||||||||
|
Оскіл ки в адачі, |
о ро |
л даєт с , |
кут 0 |
є фіксовани , то введена |
ножина функцій дійсно |
||||||||||||||
уде однопара етричною. ункці w*(x) , адані рівн нн |
. |
, дійсно арактери уют |
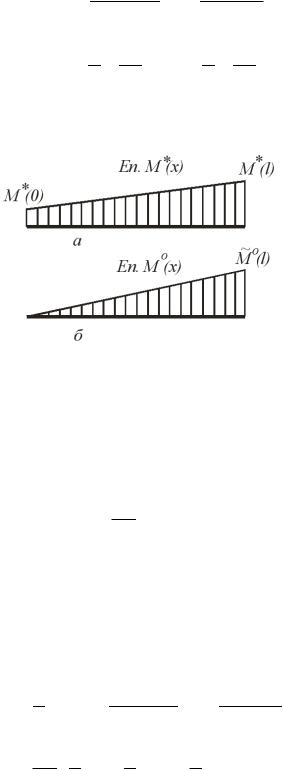
5. Енергетичні теореми і варіаційні принципи |
|
|
|
52 |
||||||
ожливі пере і |
енн , то у |
о |
ают неперервні по ідні і на підставі співвідношен . |
і |
||||||
. |
при |
уд - |
ко у пара |
етрі w |
адовол н ют раничні у |
ови . |
і . |
. |
|
|
В |
силу |
рівностей 5.55 |
і |
5.56 |
кожно у кіне атично |
ожливо |
у пере і |
енню |
ожна |
|
поставити у відповідніст внутрішні |
усилл |
|
|
|
|
|||||
|
* |
|
EI w |
d 2 |
|
1 |
x |
d 2 x |
|
M |
x |
|
|
|
0 |
|
|||
|
|
dx2 |
|
dx2 |
|||||
|
|
|
|
|
|
|
|
|
(5.122) |
|
|
|
EI w |
4 |
6x |
|
2 |
6x |
|
|
|
|
l |
l2 |
|
0 l |
l2 . |
||
Епюра M * x представлена на рис. . ,а.
|
|
|
ис. .13 |
|
|
|
|
ункці M* x , |
о |
адают с співвідношенн |
. |
, є лінійни и, до то о ж q x |
0 . |
о |
у а начені функці |
адовол н ют рівн нн |
рівнова и |
5.51 . Однак вони не належат |
до |
|
під |
ножини статично |
ожливи усил , оскіл ки в силу то о, |
о |
|
||
|
|
|
|
M * |
0 |
EI |
4w |
2 0 |
(5.123) |
|
|
|
|
l |
|||||
і природна |
ранична у |
ова на ліво |
у кінці |
алки |
M 0 0, власне кажучи, не виконуєт с . |
||||
Підставивши |
. |
до |
. |
, одержи о вира |
дл |
функціоналу |
1 w* на однопара етричній |
||
під ножині, |
о ро |
л даєт с |
|
|
|
|
|
|
|
* |
1 l |
EI w |
d 2 |
1 |
x |
|
d 2 x 2 |
|
||
|
|
|
0 |
|
|
|||||
1 w |
2 0 |
dx2 |
|
dx2 |
dx |
|||||
|
EI |
4 |
|
4 |
|
|
4 |
|
|
|
|
2 l |
w2 |
l w 0 |
l |
0 |
2 |
|
|||
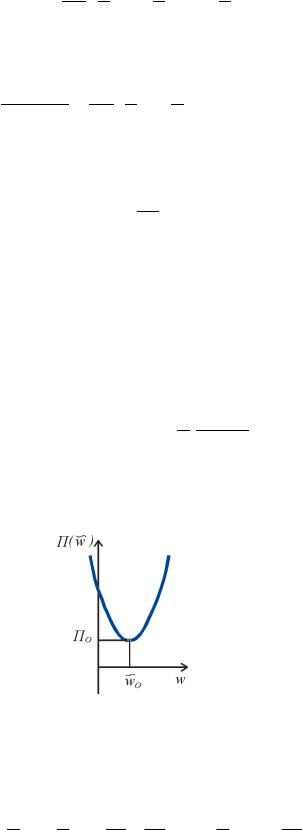
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
53 |
||||||||||
аки |
чино , |
на однопара |
етричній під |
|
ножині функціонал |
а ранжа є функцією одніє |
|||||||||
інно |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
EI |
4 |
w2 |
4 |
w 0 |
4 |
0 |
2 |
. |
(5.124) |
|
|
|
1 |
|
2 |
l |
l |
l |
||||||||
у ов стаціонарності функціоналу |
на оди |
о |
|
|
|
|
|
|
|
||||||
|
|
d 1 w |
|
EI 8 w |
4 0 |
|
0. |
|
|
|
|||||
|
|
|
dw |
|
|
2 |
|
l |
|
l |
|
|
|
|
|
Отже, стаціонарне наченн функціонал |
|
~ |
|
|
|
|
|
|
|
||||||
1 w на уває при |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
w0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
(5.125) |
|
наслідок то о, |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
~ |
|
|
4EI |
|
|
|
|
|
|
|
|
|
|
|
1 w |
|
|
0, |
|
|
|
|
|
||
|
|
|
|
|
~2 |
|
|
l |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dw |
|
|
|
|
|
|
|
|
|
|
функці |
~ |
|
|
|
~ |
|
0,5 0 на уває |
іні |
у у, |
кий дорівнює |
|||||
1 w є випуклою уни |
і в точці w0 |
|
|||||||||||||
|
|
min |
1 w0 |
|
|
1 |
|
|
|
1 3EI 2 |
|
0 . |
(5.126) |
||
|
|
|
|
|
|
0 |
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
w |
|
|
|
|
2 |
2 |
l |
|
|
|
|
||
рафік функці |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 w о ражено на рис. . . |
|
|
|
|
|
|
|
||||||||
|
|
ис. |
.14 |
Підставивши наченн |
. |
до функці . |
, отри ає о співвідношенн , о арактери ує |
дійсні наченн функці про ину |
|
|
|
w x |
x |
1 |
x 2 |
x3 |
x2 |
|
0 |
1 |
x |
x3 |
|
. |
(5.127) |
0 |
2 |
|
l |
l2 |
l |
|
2 |
|
l2 |
0 |
|
|
|
|
|
|
|
|
|
|
|

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
54 |
|||||||||||||||||||||
а підставі співвідношен |
. |
і . |
|
ожна |
|
|
аписати вира |
дл |
дійсни |
|
начен |
функці |
|||||||||||||||||||
усил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
0 |
x |
|
|
3EI 0 x. |
|
|
|
|
|
|
|
|
|
(5.128) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
о л не |
о |
надалі |
питанн |
|
одо |
|
астосуванн |
|
|
|
|
до |
адачі |
про |
ин тіє |
|
ж са |
о |
алки |
||||||||||||
див.рис. . |
|
функціоналу |
астіл |
но. В ц о |
у випадку статично |
ожливу функцію |
инал ни |
||||||||||||||||||||||||
о ентів ви начи о, ви од чи |
рівн нн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
d 2M 0 |
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
(5.129) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
і ранични |
у |
ов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
2M 0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
1 |
d |
|
|
x |
|
|
|
|
0 |
, |
|
|
|
|
|
|
|
(5.130) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
0 |
d2M 0 |
|
|
x |
|
|
|
|
0 |
. |
|
|
|
|
|
|
|
(5.131) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
l |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
раничні у ови |
. |
|
ожут |
ути аписані у фор |
|
|
і |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
M 0 0 |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.132) |
||
Ба уючис |
на рівност |
. |
|
і . |
|
|
статично |
|
|
ожливі |
усилл |
апише о наступни |
чино |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
~ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
M |
|
x |
M |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.133) |
||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
~ |
|
|
ий |
о |
ент на правій опорі. Епюра M |
0 |
x представлена на рис. |
|
. |
, . |
|
|
|
||||||||||||||||||
де M – невідо |
|
|
|
|
|
|
|||||||||||||||||||||||||
аки |
чино |
, |
|
ножина |
статично |
|
ожливи |
|
|
|
|
|
|
усил |
є однопара етричною. |
Внаслідок |
|||||||||||||||
співвідношен |
|
. |
|
і . |
|
функціонал |
астіл |
но |
(5.96 |
на |
цій |
ножині |
статично |
||||||||||||||||||
ви начувани |
усил |
на уває ви л ду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 M 0 |
|
1 l M 2 |
|
x 2 dx |
|
|
|
0 M |
1 M 2l |
0 M . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 0 EI |
|
l |
|
|
|
|
|
|
|
|
|
|
6 |
EI |
|
|
|
|
|
|
|
|||
Отже, |
на |
однопара етричній |
ножині |
статично |
ожливи |
усил , |
о |
ро |
л даєт с , |
||||||||||||||||||||||
функціонал |
астіл |
но є функцією одніє |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
інно M : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
55 |
||||||||||||||||
|
|
|
|
2 |
M |
|
|
1 M |
2l |
0 M . |
|
(5.134) |
|||||||
|
|
|
|
|
|
|
|
|
6 EI |
|
|
|
|
|
|||||
а у ови стаціонарності функціоналу |
|
~ |
|
|
|
на оди |
о |
|
|
|
|||||||||
|
2 M |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
d |
~ |
|
~ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
M |
|
|
1 Ml |
|
|
|
|
|
||||||
|
|
|
|
|
|
2~ |
|
|
|
|
|
|
|
|
0 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
3 EI |
|
|
||||||||
|
|
|
|
|
dM |
|
|
|
|
|
|
|
|
||||||
відси дійсне наченн |
о енту на право укінці |
|
алки |
|
|
|
|
||||||||||||
|
|
|
|
|
|
M |
0 |
|
3EI |
. |
|
|
|
(5.135) |
|||||
|
|
|
|
|
|
|
|
|
|
l |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е ко впевнитис |
в то |
у, |
о алежніст |
. |
|
|
|
|
іж |
о |
енто |
M 0 |
і куто повороту 0 |
||||||
і аєт с |
алежністю . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
наслідок то о, |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
M |
1 |
|
l |
|
0, |
|
|
|
||||
|
|
|
|
|
|
dM |
|
|
|
3 EI |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
функціонал |
~ |
|
|
увер |
і в точці |
~ |
|
M 0 на уває |
акси у |
у, кий дорівнює |
|||||||||
2 M є випукли |
M |
||||||||||||||||||
|
|
max |
|
|
M |
|
|
|
M0 |
|
|
3 EI |
2 |
0 . |
(5.136) |
||||
|
|
2 |
|
2 |
|
|
|
2 |
l |
0 |
|||||||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рафік функці |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 M представлено на. рис. . . |
|
|
|
|
|
||||||||||||||
|
|
ис. .15 |
Порівн вши . |
і . |
, до оди о до висновку, о ає ісце алежніст |
min |
|
w max |
|
M |
|
3 EI 2 . |
|
w |
1 |
M |
2 |
|
0 |
|
0 |
|
|
|
2 L |
||||
|
|
|
|
|
|
||
е відповідає рівності 5.103).
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
56 |
|||||||||||||||||
5.9. Прямі методи розв’язання варіаційної задачі |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
к |
уло вже |
а начено, |
|
адача статики дефор |
івни |
систе |
оже |
ути сфор |
ул ована |
к |
|||||||||||||||||||
крайова |
адача |
дл |
диференціал ни |
рівн н |
а о |
|
к |
варіаційна |
адача. |
о л ду |
|
удівел но |
|||||||||||||||||
е аніки о идва фор улюванн |
є еквівалентни и. |
Проте при ви наченні на лижени |
ро в' |
ків |
|||||||||||||||||||||||||
о начени |
|
адач тако |
еквівалентності вже не існує. |
О ранн |
то о а о іншо о фор |
улюванн |
|||||||||||||||||||||||
при водит , |
к правило, до рі ни |
процедур. |
В останні роки при по удові на лижени |
етодів |
|||||||||||||||||||||||||
ро в' ку |
адач |
удівел но |
|
е аніки перева а надаєт с |
варіаційни |
постановка |
. |
е |
у |
овлено |
|||||||||||||||||||
ти , |
о пор док по ідни |
функцій, |
кі фі уруют |
|
у варіаційни |
принципа , нижче пор дків |
|||||||||||||||||||||||
по ідни |
у відповідни |
диференціал ни |
рівн нн . |
о у у варіаційни |
під ода |
|
ви |
о и |
до |
||||||||||||||||||||
ладкості |
апрокси |
уючи |
функцій |
ожут |
ути |
посла лені. |
алі |
ро |
л дати |
ут с |
де кі |
||||||||||||||||||
на лижені |
етоди, |
кі |
а уют с |
на о начени |
варіаційни |
під ода . |
|
сі |
етоди |
рунтуют с |
на |
||||||||||||||||||
єдино |
у принципі ро шукуєт с |
де ка функці , ка надає функціоналу саціонарне |
наченн . |
|
|||||||||||||||||||||||||
По удову на лижени |
етодів ро в' |
ку крайови |
|
адач |
удівел но |
|
е аніки найприродніше |
||||||||||||||||||||||
виконувати |
а допо |
о ою пр |
и |
етодів. |
утніст |
ци |
|
етодів пол |
ає в то |
у, |
о варіаційна |
а- |
|||||||||||||||||
дача пошуку екстре |
у |
у функціоналу ро |
л даєт с |
|
к |
ранична дл |
адачі на екстре |
|
у |
функці |
|||||||||||||||||||
скінченно кіл кості |
інни . |
цією |
етою |
функці , |
ка |
іні |
і ує |
функціонал, |
а інюєт с |
||||||||||||||||||||
на лижени |
аналітични |
|
вира о |
, |
кий |
найкра |
и |
|
чино |
апрокси ує |
цю |
функцію. |
|||||||||||||||||
ай ручнішою фор |
ою тако |
а |
іни є поданн |
функці |
у ви л ді р ду |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
y |
x |
a0 0 |
x |
a1 1 |
x |
ai i |
x |
|
i |
0 |
ai i |
x , |
|
|
|
(5.137) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де i |
x |
|
так |
вані базисні функції, |
кі адают с |
|
а дале ід , |
ai |
– неви начені коефіцієнти, |
||||||||||||||||||||
кі варіюют с в такий спосі , |
о |
функці |
y x , |
ка |
|
адаєт с |
представленн |
. |
|
, надавала |
|||||||||||||||||||
функціоналу стаціонарно о |
наченн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а |
уд - |
ко о числювал но |
с е и сі |
' |
а исни |
|
функцій |
ає відповідати певни |
у ова |
||||||||||||||||||||
функці |
i |
x |
ус т |
ути лінійно не алежни и і |
ати неперервну першу по ідну. |
Під лінійно |
|||||||||||||||||||||||
алежни |
и |
слід |
ро у |
іти |
функці |
0, 1, , n , |
дл |
|
ки |
|
ожна |
найти |
такі |
константи |
|||||||||||||||
C0,C1, ,Cn, кі всі водночас не дорівнюют |
нулю, |
|
о |
виконувалас |
рівніст |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
C0 0 |
C1 1 |
Cn n |
0. |
|
|
|
|
|
|
|
|
|
|
|||||||
О начені функці вважают |
лінійно не алежни , |
к |
|
о ц |
рівніст |
|
ожлива лише а у ови |
|
|||||||||||||||||||||
C0 C1 Cn 0.
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
57 |
|||||||||||||||||||||||
|
спі |
о числювал но |
процедури, |
о |
а уєт с |
на |
пр |
и |
|
етода , |
істотно |
алежит |
від |
||||||||||||||||||||||
вдало о ви ору |
а исно |
сі |
' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
алі ро |
л дати |
ут с два типи на лижени |
|
етодів. |
|
о першо о віднос т с |
етод |
ітца та |
||||||||||||||||||||||||||
етод Бу нова- |
ал оркіна, |
де до ви |
о и лінійно |
|
не алежності |
а исни |
функці |
i |
x |
додаєт с |
|||||||||||||||||||||||||
ви о а, |
о |
вони адовол н ли певні |
раничні у ови. |
|
о дру о о типу належит |
етод |
реффца. |
||||||||||||||||||||||||||||
ут нео |
ідно, |
о |
а исні функці адовол н ли рівн нн |
Ейлера відповідно варіаційно |
адачі. |
||||||||||||||||||||||||||||||
5.9.1. Метод Рітца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
перше варіаційний під ід дл |
по удови на лижено о ро в' |
ку |
а допо |
о ою пр |
о о |
етоду |
||||||||||||||||||||||||||||
ув |
апропонований В. |
|
ітце |
у |
|
р. Викладе |
|
о |
етод |
ітца на прикладі варіаційно о принципу |
|||||||||||||||||||||||||
а ранжа |
див.п. . |
серед кіне |
атично ожливи |
пере |
і |
ен |
|
y |
x дійсне пере |
і |
енн |
надає |
|||||||||||||||||||||||
повній потенціал ній енер і |
1 y стаціонарно о |
|
наченн |
0 . |
к уло ви начено в п. |
. |
, |
це |
|||||||||||||||||||||||||||
стаціонарне |
наченн |
є |
|
іні |
у о |
функціоналу. |
|
іне |
атично |
ожливі |
пере |
і енн |
|
|
ус т |
||||||||||||||||||||
ати неперервну першу по ідну і |
|
адовол н ти |
кіне |
атичні |
раничні |
у ови |
(5.54 . |
Отже, |
|||||||||||||||||||||||||||
ви ирає о систе у |
а исни |
функцій |
|
i |
x |
n |
|
, |
де |
0 |
x |
адовол н є неоднорідні, а |
|
i |
x |
– |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
однорідні кіне |
атичні у |
ови |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1d1yi |
x |
x |
a |
|
|
0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
I1d1yi |
x |
|
x |
b |
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
а лижений ро в |
ок варіаційно |
|
адачі шукати |
е |
о у ви л ді |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
n |
ai i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
x |
|
|
|
x . |
|
|
|
|
|
|
|
(5.138) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аки |
чино , |
а уд - ки поки |
|
е |
не |
|
ви начени |
коефіцієнта |
ai |
функці |
y |
|
x |
||||||||||||||||||||||
адовол н є |
раничні у |
ови (5.54 дл |
|
дано |
варіаційно |
|
адачі. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
а лижений ро в' |
ок |
удуєт с |
наступни |
|
чино |
|
серед усі |
функцій . |
|
ви начи |
о |
|||||||||||||||||||||||
таку, |
о |
іні |
і ує |
|
1 y . |
Підставивши . |
|
|
у функціонал |
5.78 |
пере оди |
о до |
функці |
||||||||||||||||||||||
невідо и |
коефіцієнтів |
ai . |
Пошук |
величин ци |
|
коефіцієнтів |
виконуєт с , |
ви од чи |
|
|
у |
ов |
|||||||||||||||||||||||
іні |
і аці функці , |
кі |
|
ают |
ви л д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
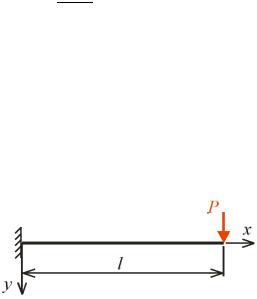
5. Енергетичні теореми і варіаційні принципи |
58 |
|
|
|
|
|
|
0 (i=1,2, ... ). |
|
(5.139) |
|
|
|
|
|
|
i |
|
|||
|
|
|
|
|
|
|
|
|
|
ре ул таті ає о систе |
у ал е ра чни |
рівн н . При виконанні практични |
ро ра унків |
||||||
нескінченний р д . |
а |
інюют |
су ою скінченно кіл кості членів . |
. |
оді систе |
а |
|||
рівн н |
ає скінченний пор док, але |
ро в |
|
ок стає на лижени . |
|
|
|
||
Приклад 5.4. Ви начити а |
етодо |
ітца про ини у консол ній алці, навантаженій на віл но |
у |
||||||
кінці |
осередженою силою |
рис. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. |
.16 |
|
|
|
||
дано у випадку кіне |
атичні раничні у ови однорідні, то |
у 0 |
x 0 . |
|
|||||||||||
Шукати |
е |
о функцію про инів у ви л ді |
|
р ду |
|
|
|
||||||||
|
|
|
|
|
y x a1x2 |
a2 x3 an xn 1, |
|
||||||||
то то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
x |
xi 1 . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ожна впевнитис |
о кожна |
|
функцій i |
|
x |
адовол н є кіне |
атичні раничні у |
ови |
|||||||
при |
x |
0 |
i |
x |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
1 |
xi 0 |
i |
|
2,3, ,n ; |
|
|
|
||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
і не адовол н є статичні. |
ак, |
|
|
|
|
|
|
|
|
|
|
||||
при x |
l |
1 |
x |
2 |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
6l |
|
0. |
|
|
|
|
|
|
|
|
Отже, |
ожна |
ска ати, |
о вс |
апрокси |
уюча функці |
y x |
адовол н є кіне |
атичні і не |
|||||||
адовол н є статичні раничні у |
ови. |
|
|
|
|
|
|
|
|||||||
Повна потенціал на енер і |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
U A |
EI |
l |
y x 2dx Py l . |
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
5. Енергетичні теореми і варіаційні принципи |
59 |
||
о |
л не |
о функцію про инів у ви л ді y x a x2 , то то ері ає о один член р ду. |
оді |
|
|
1 |
|
y x |
2a , |
y l a l 2 . Повна потенціал на енер і в ц о у випадку |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
EI l |
2a |
|
|
|
2dx |
|
|
Pa l2 . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
у |
ови екстре |
ал ності повно потенціал но |
|
енер і |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
4EIa l |
|
Pl2 |
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
da1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
дістає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
Pl |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4EI |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
івн нн |
про инів апишет с |
у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
|
|
Pl |
|
x2 , |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4EI |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а на віл но |
у кінці алки при x |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y l |
|
|
Pl3 |
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4EI |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
очний ро в |
ок дано |
адачі y l |
|
|
|
|
Pl3 |
, то то по и ка становит |
|
. |
|||||||||||||||||||||
|
|
|
|
3EI |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
к |
о в функці про инів утри |
ати два члени р ду |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
y x |
|
a x2 |
|
|
a |
2 |
x3 |
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то дру а по ідна становити |
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
y |
|
|
x |
|
2a1 |
|
6a2 x , |
|
|
|
||||||||||||
і повна потенціал на енер і |
ати |
е ви л д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
U A |
|
EI l |
|
|
2a 6a |
2 |
x |
|
2 dx P a l2 |
a |
2 |
l3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. Енергетичні теореми і варіаційні принципи |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
4a2l 12a a |
2 |
l |
2 12a2l3 |
P a l 2 |
a |
2 |
l3 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ови екстре у |
у функці |
П: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4Ela |
6EIa l2 |
|
|
|
Pl2 |
|
|
0, |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EIa l2 12EIa |
2 |
l3 |
|
|
Pl3 0. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
о в |
ок ціє |
систе и дво ал е ра чни |
рівн н |
|
|
ви начає невідо |
і коефіцієнти р ду |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
Pl |
, |
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
P |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
6EI |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отже, функці |
про инів вира ит с |
|
співвідношенн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
|
|
Pl |
|
x2 |
|
|
|
|
|
P |
|
x3. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI |
|
|
6EI |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При x |
l y l |
|
Pl |
l |
2 |
|
|
P |
|
|
l |
3 |
|
|
Pl3 |
|
, |
о |
|
і аєт с |
|
точни |
ро в |
ко . |
|||||||||||||||||||||||
|
2EI |
|
|
|
6EI |
|
|
|
|
|
3EI |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
к |
о ж утри |
ати три члени р ду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y x a x2 |
|
a |
2 |
x3 |
|
|
|
a |
3 |
x4 |
, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то післ |
анало ічни |
о числен |
дістає |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
Pl |
, |
|
|
a |
2 |
|
|
|
|
Pl |
|
, |
|
|
|
a |
3 |
0 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2EI |
|
|
|
|
|
|
6EI |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
івніст |
нулю чер ово о члена р ду |
в дано |
у випадку a3 |
свідчит про дос |
|
ненн точно о |
|||||||||||||||||||||||||||||||||||||||||
ро в |
ку |
адачі. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Канонічні рівняння методу Рітца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
л |
а ал но о випадку поперечно о |
|
ину стержн повна потенціал на енер і |
ви начаєт с а |
|||||||||||||||||||||||||||||||||||||||||||
фор улою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
A |
|
l EI |
|
y |
2 dx |
|
l qydx |
|
|
|
|
|
|
Pyp |
Mym , |
|
|
(5.140) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

5. Енергетичні теореми і варіаційні принципи |
61 |
||
де два останні доданки |
арактери уют |
вплив осереджени сил і |
о ентів, y p , ym про ини |
стержн відповідно в ісц |
прикладанн |
осереджени сил P і о |
ентів M рис. . . |
ис. .17 дано у випадку кіне атичні раничні у ови також однорідні, то у ада о про ини у ви л ді
р ду
|
|
|
|
|
|
|
|
|
|
|
n |
ai i , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
(5.141) |
|||
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
де |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ожна |
аписати, |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
yn |
|
ai i , |
|
yn |
|
ai . |
|
|
|
(5.142) |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
i |
1 |
|
|
|
|
Післ |
підстановки |
апрокси |
уючо |
функці |
та |
по ідни |
у |
функціонал 5.140 останній |
|||||||||||
перетворюєт с |
на функцію |
а ат о |
|
інни |
a1,a2 , ,an . |
ова и екстре у |
у ціє функці |
||||||||||||
уде дорівнюванн |
нулю окре и |
по ідни |
по кожно |
у |
невідо |
и |
пара |
етрів |
|
||||||||||
|
|
|
|
|
|
|
a1, a2 , ,an |
0 |
|
k |
1,2,...,n |
|
|
|
(5.143) |
||||
|
|
|
|
|
|
|
ak |
|
|
|
|
|
|
|
|
|
|
|
|
а о у ро |
орнуто |
уви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
l |
n |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
ai i k dx |
|
q k dx |
P k |
xp |
M k xm |
0. |
(5.144) |
||||||
|
|
|
ak |
|
|
||||||||||||||
|
|
|
0 |
i |
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||
апише |
о у |
ову . |
дл кожно о k почер ово |
|
|
|
|
|
|
||||||||||
При k=1 |
l |
EI |
1 |
2 dx |
a1 |
l |
EI |
1 2 |
dx |
a2 |
|
l |
EI |
1 n |
dx an |
|
|||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
62 |
||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q 1dx |
P 1 |
xp |
M 1 xm , |
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
k=2 |
l |
EI |
2 1 |
dx a1 |
l |
EI 2 |
2 dx |
a2 |
l |
EI |
2 n |
dx |
an |
|||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q 2dx |
P 2 |
xp |
M 2 |
|
xm |
, |
|
|
|
|
|
|
(5.145) |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... |
|
|
|
|||||||||||
При |
k=n |
l |
EI |
n 1 |
dx a1 |
l |
EI n 2 |
dx |
a2 |
|
l |
EI |
n |
2 dx |
an |
||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q ndx |
P n |
xp |
M n xm . |
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
о по начити |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kij |
EI i jdx , |
|
|
|
|
|
|
|
|
(5.146) |
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rjp |
q j |
x dx |
P j |
xp |
M j |
|
xm |
, |
|
(5.147) |
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
то рівн нн |
. |
|
ожна переписати у так |
|
ваній канонічній формі: |
|
|
||||||||||
|
|
|
|
|
k11a1 |
k12a2 |
k1nan |
R1p , |
|
|
|
|
|
||||
|
|
|
|
|
k21a1 |
k22a2 |
k2nan |
R2 p , |
|
|
|
|
(5.148) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
kn1a1 |
kn2a2 |
knnan |
Rnp . |
|
|
|
|
|
||||
о |
л не |
о випадок неоднорідни |
ранични |
у |
ов. |
е ай в попередній адачі раничні у ови |
|||||||||||
удут |
неоднорідни |
и рис. . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y 0 |
|
y0 , |
y l |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
0, |
y l |
l . |
|
|
|
|
|
|
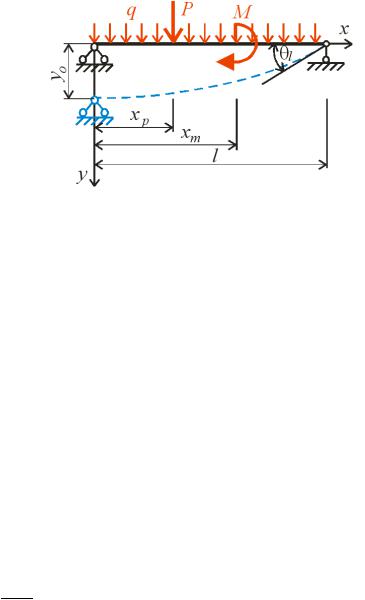
5. Енергетичні теореми і варіаційні принципи |
63 |
|
|
|
|
|
|
|
|
ис. .18 |
|
|
|
оді |
ожливе пере |
і |
енн |
yn |
x |
ро шукуєт с у ви л ді |
|
||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
yn |
x |
0 x |
ai i |
x , |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
де 0 x |
адовол н є |
адани |
неоднорідни |
, а всі інші i |
x – однорідни ранични у ова . |
||||||
Відповідно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
yn |
x |
0 x |
ai i |
x , |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
yn |
x 0 x |
ai i |
x . |
|
||
|
|
|
|
|
|
|
|
i |
1 |
|
|
ц о |
у випадку рівн нн . |
|
на уває ви л ду |
|
|
|
|||||
|
|
|
l |
n |
|
|
|
|
l |
|
|
|
|
EI |
|
ai i |
x k x dx |
EI 0 |
x k x dx |
||||
|
ak |
|
|||||||||
|
0 |
i 1 |
|
|
|
o |
|
|
|||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
q k x dx |
P k |
xp |
M k xm |
0. |
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
Отже, |
нову при оди |
о до систе |
и рівн н . |
, але |
іншою правою частиною |
||||||
|
|
l |
|
|
|
|
|
l |
|
|
|
|
Rjp |
|
EI 0 |
x j |
x dx q j x dx |
P j |
xp M j xm . |
||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
Приклад 5.5. По удувати систе |
у канонічни рівн н а етодо |
ітца дл консол но алки |
|
див.рис. . ), о ула ро |
л нута у прикладі . . |
|
|
При складанні рівн н о |
ежи |
ос дво а члена и р ду апрокси |
уючо функці про инів |
5. Енергетичні теореми і варіаційні принципи |
64 |
|
|
|
|
|
|
|
|
y x |
|
a x2 |
|
a |
2 |
x3 . |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
о то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
, |
|
|
|
|
2 |
|
x3 , |
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2, |
|
|
|
|
|
2 |
|
6x. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, |
ати е о систе |
удво |
канонічни рівн н |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
k11a1 |
k12a2 |
|
R1 p , |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
k21a1 |
k22a2 |
|
R2 p . |
|
|
|
|||||||||||
О числи |
о коефіцієнти при невідо |
и |
|
пара |
|
етра |
|
|
а допо |
о ою |
5.146): |
|
|||||||||||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k11 |
|
EI 1 1dx |
|
|
|
|
EI |
|
2 |
2dx |
4EI l, |
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
k |
|
k |
21 |
|
|
EI |
2 |
dx |
|
|
EI |
2 |
6xdx |
6EI l2, |
|||||||
|
|
|
|
12 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
22 |
|
EI |
2 |
|
2 |
dx |
|
|
|
|
EI |
6x |
6xdx 12EI l3. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
л о численн віл ни |
членів скористує |
|
ос |
співвідношенн |
5.147 , |
еручи до ува и, о |
|||||||||||||||||||
інтенсивніст |
ро поділено о навантаженн |
|
q і величина |
осереджено о о |
енту M дорівнюют |
||||||||||||||||||||
нулю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
P |
|
|
|
l |
|
Pl2 , |
|
|
|
|||||
|
|
|
|
|
|
|
|
1p |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
R |
|
|
|
P |
|
|
2 |
l |
|
|
Pl3. |
|
|
|
|||
|
|
|
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, |
ає |
о систе |
урівн н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4EI la |
|
|
6EI l2a |
|
|
Pl2 |
, |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI l2a 12EI l3a |
|
|
Pl3 |
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ка і аєт с |
систе |
ою, |
о ула одержана в прикладі . . |
|
|
|
|||||||||||||||||||
5.9.2. Метод Бубнова-Гальоркіна
етод увійшов до практики е аніки к етод ро в анн диференціал ни рівн н , то то спочатку цей етод не ав варіаційно о фор улюванн .
е ай адача ведена до ро в анн де ко о диференціал но о рівн нн
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
65 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L x, y, y , y , |
q |
0, |
|
|
|
|
|
|
|
(5.149) |
||||||||
де |
y |
y x |
|
невідо а функці , |
раничні у |
ови |
ко |
адані, |
q |
|
q x |
|
відо |
а функці , |
о |
|||||||||||||
арактери ує |
овнішнє навантаженн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
а лижений ро в |
ок рівн нн |
. |
|
ро шукує |
о у ви л ді |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y |
x |
|
0 |
x |
|
|
|
ak k |
x , |
|
|
|
|
|
|
|
(5.150) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
де |
а исна функці |
0 x |
повинна |
адовол н ти всі |
адані |
раничні у |
|
ови, а |
а исні функці |
|||||||||||||||||||
k |
x |
– однорідні |
раничні у |
ови, |
к кіне атичні, |
так і статичниі. Вважаючи ці функці |
а відо |
і, |
||||||||||||||||||||
уде о ро шукувати пара етри ai . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Оскіл ки |
а исні |
функці |
адовол н ют |
|
всі |
|
раничні |
у ови, |
неінте рал ні |
члени |
в 5.33) |
||||||||||||||||
е ают |
і алишаєт с |
у ова |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x, y, y , y , |
q i |
x |
0 |
i |
1,2, ,n |
|
|
|
|
(5.151) |
|||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
о рівн нн |
. |
є лінійни |
стосовно невідо |
о |
функці |
та |
по ідни , то рівніст |
. |
|
|||||||||||||||||
становит |
систе |
у лінійни |
ал е ра чни |
рівн н |
відносно невідо |
и |
коефіцієнтів ai . О начена |
|||||||||||||||||||||
систе |
а |
аписана, |
ви од чи |
|
ви о и орто онал ності нев' |
ки рівн нн |
. |
післ |
підстановки |
|||||||||||||||||||
до н о о систе и |
|
а исни |
|
функцій . |
|
. |
к |
о |
. |
|
є рівн нн |
|
Ейлера |
дл |
де ко |
|||||||||||||
варіаційно |
адачі |
однорідни и |
ранични |
и у |
ова и, то систе |
а . |
|
оже |
ути на ута |
|||||||||||||||||||
у ови |
іні у у функціоналу. |
При однорідни |
ранични |
у ова |
а |
іст |
|
. |
астосовуєт с |
|||||||||||||||||||
представленн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x |
|
|
ak k |
x . |
|
|
|
|
|
|
|
|
(5.152) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оді варіаці |
аписуєт с |
наступни |
чино |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x |
|
ak k |
x . |
|
|
|
|
|
|
|
(5.153) |
||||||
k1
ко прирівн ти до нул варіацію повно потенціал но енер і 5.33 і підставити до не
представленн |
. |
і . |
, то отри ає о рівн нн |

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
66 |
|||||||||||||||||
|
|
|
|
|
|
|
d F |
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
F |
|
|
|
|
a |
|
F |
a |
|
|
|
|
||||||
|
|
|
|
|
y |
|
dx |
y |
|
|
|
|
i |
i |
y |
i |
i |
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
dF |
|
|
d 2 F |
|
|
ai i dx |
|
|
|
|
|
|
||||
|
|
|
|
|
Fy |
y |
|
|
|
|
y |
|
|
0. |
|
|
|
(5.154) |
|||||
|
|
|
|
|
dx |
|
|
|
dx2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Перепише |
о |
а начене рівн нн у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
b |
|
dFy |
|
d |
2 |
Fy |
|
|
|
|
|
d |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
F |
|
|
|
|
x |
F |
F |
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i 1 |
y |
|
dx |
|
dx2 |
|
|
i |
|
y |
dx |
y |
i |
a |
(5.155) |
||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Fy |
i |
x ba |
|
ai |
|
|
0. |
|
|
|
i |
1,2, ,n |
|
|
||||
|
наслідок довіл ності варіаці |
ai і |
співвідношенн . |
ає |
|
о |
|
|
|||||||||||||||
b |
|
dFy |
d 2 F2y |
|
|
|
|
d |
|
|
|
|
|
|
|
b |
|
ba |
|
|
|
|
|
Fy |
i x |
|
Fy |
|
Fy |
i |
|
x |
Fy i |
x |
|
0. |
i =1,2, ,n |
(5.156) |
|||||||||
a |
|
dx |
|
dx |
|
|
|
|
dx |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Оскіл ки |
а исні функці |
адовол н ют |
і кіне |
атичні і |
силові однорідні раничні |
у ови, |
||||||||||||||||
неінте рал ні члени в рівн нн |
|
. |
|
о ертают с на нул , і |
и отри ує |
о систе у 5.151). |
|||||||||||||||||
|
Приклад 5.6. |
Ви начити про ин посередині |
|
алки на дво |
опора , |
о пере уває під дією |
|||||||||||||||||
рівно |
ірно ро поділено о навантаженн |
q див. рис. . ). |
|
|
|
|
|
|
|||||||||||||||
|
иференціал не рівн нн рівнова и одержано в прикладі . |
: |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
q |
|
|
d 2 |
|
|
EIy |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|||||
Перепише о рівн нн у ко пактнішо у ви л ді
EIyIV q 0.
Шукати е о ро в ок у ви л ді р ду
y x |
ak k x |
|
aksin |
k x |
. |
|
|
||||
|
k 1,3, |
k 1,3, |
|
l |
|
|
|
|
|
||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
67 |
|||||||
Ба исні функці відповідают |
к кіне |
атични |
, так і статични |
ранични |
у |
ова . |
правді, на |
||||
ліво |
у |
кінці |
алки |
при x |
ає о |
k 0 |
0, k 0 0, |
на право |
у |
кінці |
при x=l) |
k |
l |
0, k |
l |
0 . |
|
|
|
|
|
|
|
|
етверта по ідна від а исно |
функці |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV |
|
x |
|
|
|
|
k4 4 |
sin |
k x |
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
l4 |
|
l |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
л ро ра унку о |
ежи |
о кіл кіст |
|
|
членів р ду дво |
а члена и |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
a sin x |
|
|
a |
3 |
sin |
3 x |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Підставл ючи одержане диференціал не рівн нн |
до у |
ови орто онал ності |
5.151 ура уван- |
|||||||||||||||||||||||||||||||||||||||||||
н апрокси |
аці |
про инів, |
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
l |
|
|
|
4 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
34 |
4 |
|
|
|
|
3 x |
|
|
|
|
|
|
k x |
|
|
|||||||||||||
|
EI |
a |
sin |
|
|
a |
|
|
|
|
|
sin |
|
|
q |
sin |
dx 0 k |
1,3 . |
||||||||||||||||||||||||||||
|
l 4 |
|
|
|
|
|
|
|
|
|
|
|
|
l 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
0 |
|
1 |
|
|
|
|
l |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
апише о це рівн нн |
почер ово дл |
кожно о наченн |
k: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
l |
|
|
|
4 |
|
|
|
x |
|
|
|
|
|
|
81 |
4 |
|
|
|
|
|
3 x |
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||
|
EI |
a |
sin |
|
|
a |
3 |
|
|
sin |
|
|
|
q |
sin |
dx |
0 , |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l 4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
0 |
|
1 l |
4 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
4 |
|
|
|
x |
|
|
|
|
|
|
81 |
4 |
|
|
|
|
|
3 x |
|
|
|
|
|
|
3 x |
|
|
|
|
|||||||||||||
|
EI |
a |
sin |
|
|
a |
|
|
|
sin |
|
|
|
q |
sin |
dx |
0 . |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
1 l |
4 |
|
|
|
l |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При виконанні інте руванн |
|
|
важи |
|
|
о на те, |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
n x |
|
|
|
|
|
|
|
|
m x |
|
|
|
|
|
|
l 2 |
при n |
|
m, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
sin |
sin |
dx |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 при n |
m, |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
l |
|
|
|
|
|
n x |
|
|
|
|
|
|
|
|
|
2ql |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
q sin |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рештою |
ає |
о |
a |
|
|
4ql 4 |
|
, a |
|
|
|
|
|
|
|
|
|
|
4ql 4 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
5EI |
|
|
|
|
|
|
|
|
243 5EI |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|||||||||||||||||||||||||||
Отже, на лижене рівн нн |
про инів |
алки |
апишет с |
у ви л ді |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
4ql 4 |
|
x |
|
4ql 4 |
|
|
|
|
|
3 x |
|
4ql 4 |
|
|
|
x |
|
|
1 |
|
3 x |
|
||||||||||||||
|
|
y |
|
|
|
sin |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
sin |
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5EI |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5EI |
|
l |
|
|
243 5EI |
|
|
l |
|
|
|
l |
|
|
243 |
|
l |
|
||||||||||||||||||||
Про ин в середині про ону при x l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
4ql 4 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
ql 4 |
|
|
|
|
||||||||
|
|
|
|
|
y l |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1.304415 10 |
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
5EI |
243 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|||||||||
очне |
наченн |
про ину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y l |
2 |
|
|
5ql 4 |
|
1,30208 10 |
|
2 |
|
ql 4 |
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
384EI |
|
|
|
EI |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Відносна по и ка становит |
, |
7 %. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
к |
о від овитис |
від однорідності |
ранични у |
ов і скористатис |
представленн |
5.152 , то |
||||||||||||||||||||||||||||||||||
вира |
дл |
варіаці , |
к і раніше, |
|
уде ви начатис |
співвідношенн |
|
|
|
5.153 , проте в рівн нн |
||||||||||||||||||||||||||||||
(5.156 |
неінте рал ні члени |
|
ожут |
не |
е нути. Анало ічною |
|
уде ситуаці , к |
о а исні функці |
||||||||||||||||||||||||||||||||
адовол н ти ут |
лише |
кіне атичні |
раничні у |
ови. |
исте а рівн н |
|
. |
|
становит |
|||||||||||||||||||||||||||||||
канонічну систе |
у рівн н |
у а ал нено о етоду Бу нова- |
ал оркіна. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.9.3.Метод Треффца
а від іну від етодів ітца і Бу новаал оркіна в етоді реффца а исні функці k x в
р ді
|
|
|
|
|
y |
x |
ak k x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
до ирают с так, |
о |
кожна ни |
становила частинний ро в |
ок диференціал но о рівн нн . В |
|||||||||||
тако у ра і всі інте рал ні члени рівн нн |
Ейлера тотожно дорівнюют нулю. |
ор |
а ро в |
ку |
|||||||||||
рівн н ітца |
5.139 |
не |
інюєт с , але в рівн нн |
вра овуют с |
лише неінте рал ні члени |
і |
|||||||||
співвідношенн |
5.33): |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
d F |
|
b |
|
|
x b |
|
|
|
|
|
|
|
|
|
F |
|
x |
F |
|
0. |
|
(5.157) |
||||
|
|
|
|
y |
dx |
y |
i |
|
y |
i |
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 5.7. |
найти |
вертикал не |
пере і |
енн |
віл но о |
кінц |
алки від |
ді |
рівно ірно |
||||||
ро поділено о навантаженн |
рис. . |
а |
етодо |
реффца. |
|
|
|
|
|
|
|||||

5. Енергетичні теореми і варіаційні принципи |
69 |
ис.5.19
Повна потенціал на енер і виражаєт с чере про ини алежністю
l
0
а о
EI |
y 2 dx |
l |
|
qydx |
|||
2 |
|||
|
0 |
||
|
|
||
|
l |
|
F y, y dx,
0
де по начено F y, y |
|
EI |
y |
2 qy . |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
иференціал не рівн нн |
рівнова и одержи |
о |
а допо о ою рівн нн Ейлера 5.35), |
||||||||
анало ічно то у, |
к це |
уло ро лено в прикладі . |
: |
|
|
|
|||||
|
|
|
|
|
EI yIV |
q |
0 . |
|
|
|
|
Ві е о апрокси |
уючий поліно у ви л ді |
|
|
|
|
|
|
||||
|
|
|
|
|
y a x2 |
a |
2 |
x3 |
a |
3 |
x4 . |
|
|
|
|
|
1 |
|
|
|
|
||
етверту по ідну від функці |
про инів |
|
|
|
|
|
|
||||
|
|
|
|
|
yIV |
|
24a3 |
|
|
|
|
підстави о в одержане диференціал не рівн нн
EI 24a3 q 0,
відки
q a3 24EI .
Отже, поліно оже ути представлений у ви л ді

5. Енергетичні теореми і варіаційні принципи |
70 |
|
|
|
|
|
y |
a x2 |
a |
2 |
x3 |
|
qx4 |
|
, |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
24EI |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то то |
к |
су а |
а ал но о ро в |
ку |
однорідно о |
диференціал но о рівн нн і частинно о |
||||||||||
ро в |
ку. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ру а і трет |
по ідні |
апишут с |
к |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
2a |
6a |
2 |
x |
|
qx2 |
, |
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
2EI |
|
|
||
|
|
|
|
|
|
|
|
|
qx |
|
|
|
|
|||
|
|
|
|
|
y |
6a2 |
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
EI |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ідно |
по наченн |
и (5.32) оже |
о аписати |
|
|
|
|
|
|
|
||||||
F |
F |
|
EI |
y |
y |
y |
y |
2 |
|
F |
F |
|
EI |
y |
y |
y |
y |
2 |
|
F |
F |
|
EI |
y |
y |
y |
y |
2 |
|
2
2
2
qy q,
qy 0,
qy EIy .
Ба исні функці і по ідні від ни
|
x2 , |
|
2 |
x3; |
|
1 |
|
|
|
||
|
2x, |
|
2 |
3x2. |
|
1 |
|
|
|
|
|
л одержанн першо о рівн нн підставл є о а исну функцію 1 та всі інші величини в
(5.157):
|
|
|
|
d F |
l |
|
|
|
l |
|
|
|
|
|
|
F |
|
F |
|
0, |
|
|
|||||
|
|
|
y |
dx |
y |
1 |
y |
|
1 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qx |
l |
|
|
|
|
|
|
qx2 |
|
l |
|
|
|
|
|
|
|
|
|
|
|
||||
EI 6a |
2 |
x2 |
|
EI 2a |
6a |
2 |
x |
2x |
0, |
||||
|
|
|
|
||||||||||
|
EI |
0 |
|
1 |
|
|
|
2EI |
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тоді
4EI la 6EI l2a |
2 |
0. |
1 |
|
Підставл ючи у 5.153 а исну функцію 2 , дістає о

5. Енергетичні теореми і варіаційні принципи |
|
|
71 |
|||||||||||||
|
d |
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
|
F |
|
F |
|
2 |
|
|
F |
|
2 |
0, |
|
|
|
|||
y |
dx |
y |
|
|
0 |
|
y |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qx |
|
|
l |
|
|
|
|
|
qx2 |
l |
|
|
EI 6a |
|
|
|
x3 |
|
|
EI 2a |
6a x |
3x2 |
0, |
||||||
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
EI |
|
|
|
|
|
|
|
1 |
2 |
2EI |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6EIl |
2a |
12EIl |
3a |
|
ql4 |
0. |
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
о в уючи систе |
у дво |
|
ал е ра чни |
рівн н , |
на оди |
о величини пара |
етрів |
|||||||||
|
|
|
a |
|
|
|
ql 2 |
, |
|
|
|
a |
2 |
|
|
ql |
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
4EI |
|
|
|
|
|
|
|
6EI |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отже рівн нн про инів |
алки на уває ви л ду |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
y |
|
ql 2 |
x2 |
|
|
ql |
x |
3 |
|
|
q |
|
x4. |
||||||
|
|
|
|
4EI |
|
|
6EI |
|
|
24EI |
|
|
||||||||||
а віл но |
у кінці |
алки при x=l: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y l |
|
|
ql 4 |
|
|
ql 4 |
|
|
ql 4 |
|
|
ql 4 |
, |
||||||
|
|
|
|
|
4EI |
|
6EI |
|
24EI |
|
8EI |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
о і аєт с |
точни |
ро в |
ко . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.10. Метод скінченних елементів як прямий варіаційний метод
|
Одни |
і |
найефективніши |
сучасни |
етодів ро ра унків є |
етод скінченни |
еле |
ентів |
Е . |
||||||||||||||||||
О начений |
етод |
ожна ро |
л дати |
к окре |
ий випадок |
етоду |
|
ітца див.п. . |
. |
, коли |
а |
а исні |
|||||||||||||||
ви ирают с |
де кі специфічні функці , |
о |
ают |
локал ний |
арактер на досліджуваній о ласті. |
||||||||||||||||||||||
л |
по удови ци |
функцій ро ра ункова с е а пружно |
систе |
|
и, |
ка |
ає нескінченну кіл кіст |
|
|||||||||||||||||||
ступнів |
віл ності, |
а |
інюєт с |
оделлю, |
напружено-дефор |
ований |
стан |
ко |
ви начаєт с |
|
|||||||||||||||||
скінченною кіл кістю пара |
етрів. |
к о пара |
етри |
арактери уют |
дефор |
ований стан |
оделі, |
||||||||||||||||||||
кажут |
про |
|
етод скінченни |
еле |
ентів у фор |
і |
етоду пере |
і |
ен . |
|
ра і, |
коли пара етри |
|||||||||||||||
ви начают |
|
напружений стан, кажут про |
етод скінченни еле |
ентів у фор |
і |
етоду сил. |
|
|
|||||||||||||||||||
|
Процедури |
етодів ро ра унків стержневи |
систе певною |
ірою |
і ают с |
процедурою |
|||||||||||||||||||||
етоду |
скінченни |
еле |
ентів |
дл |
ро в' |
ку варіаційни |
адач. |
ожна послідовно ро |
л дати |
||||||||||||||||||
стержневу систе у |
к таку, |
о складаєт с |
|
дефор |
івни |
еле ентів і скінченни |
число |
ступнів |
|||||||||||||||||||
віл ності, |
так |
вани скінченни еле ентів. |
л |
|
ожливості одержанн точно о ро в' |
ку окре |
і |
||||||||||||||||||||
еле |
енти ви ирают с |
ко |
о а простіши |
и. |
к правило, в стержневи |
систе |
а |
– це окре |
і |
||||||||||||||||||
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|||||||||||||||||||||||
стержні. Ба исні функці |
|
удуют с на основі поліно |
іал но |
інтерпол ці |
чере |
ву лові |
наченн |
|||||||||||||||||||||||||||||
на окре и |
скінченни |
|
еле |
ента . |
|
аки |
чино |
, |
напружено-дефор |
ований |
стан |
еле |
ентів |
|||||||||||||||||||||||
повністю ви начаєт с |
пере |
і |
енн |
и а о сила |
и на |
ні |
кінц |
|
, то то в точка |
сполученн |
||||||||||||||||||||||||||
еле ентів. |
|
акі |
точки |
на ивают |
ву ла и. |
а |
цій |
підставі |
ожна |
вважати, |
о |
напружено- |
||||||||||||||||||||||||
дефор |
ований |
стан |
всіє |
|
оделі |
ви начаєт с |
пере |
і |
енн |
и і силови и ді |
|
и в скінченній |
||||||||||||||||||||||||
кіл кості |
ву лови |
точок. |
|
о у таку ро ра ункову |
|
одел |
на ивают |
дискретною. |
овнішнє |
|||||||||||||||||||||||||||
навантаженн |
|
на еле енти приводит с |
до ву лів. Вважаєт с , |
о потенціал на енер і |
адано |
|||||||||||||||||||||||||||||||
с е и |
та |
|
дискретно |
|
оделі еквівалентні. Вира ивши |
потенціал ну |
енер ію |
оделі |
чере |
|||||||||||||||||||||||||||
ви начал ні |
пара |
етри, |
|
ожна |
одержати |
систе |
у |
ро в |
увал ни |
|
рівн н |
відносно |
ци |
|||||||||||||||||||||||
пара етрів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ре ул таті |
адача |
|
про |
рівнова у |
стержнево |
систе |
и |
водит с |
до |
адачі |
про |
рівнова у |
||||||||||||||||||||||||
скінченно |
кіл кості ву лів, |
|
о |
'єднуют |
еле |
енти |
іж со ою. В свою чер у, адача про рівнова у |
|||||||||||||||||||||||||||||
скінченно |
кіл кості |
ву лів |
описуєт с |
скінченною |
систе |
ою лінійни |
ал е ра чни |
рівн н . |
||||||||||||||||||||||||||||
Оскіл ки |
кожен |
|
еле |
ентів ро ра овувавс |
точно, то дл |
сукупності ву лів такий під ід дає |
||||||||||||||||||||||||||||||
точний |
ро в' |
ок. |
|
аки |
чино |
, |
адача ро ра унку |
лінійно |
дефор |
івно |
стержнево |
систе и |
||||||||||||||||||||||||
приводит с |
до |
адачі лінійно ал е ри. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
оловною перева ою |
етоду скінченни |
еле |
ентів є |
ожливіст |
порівн но просто |
удувати |
||||||||||||||||||||||||||||||
а исні функці |
дл |
|
широко о спектру |
адач. |
Причо |
у ці функці |
внаслідок сво о локал но о |
|||||||||||||||||||||||||||||
арактеру створюют |
систе |
у, |
ка є |
|
ли |
кою до орто онал но . |
акий ефект у великій |
ірі |
||||||||||||||||||||||||||||
у овлюєт с |
|
|
ожливістю |
використанн |
функцій, |
|
кі |
є |
не |
сповна |
|
ладки |
и |
і |
дл |
|
ки |
|||||||||||||||||||
диференціал на постановка |
адачі втрачає |
уд - |
кий сенс. |
е пов' |
ано |
ти |
, |
о диференціал на |
||||||||||||||||||||||||||||
і варіаційна |
постановка |
адачі пред' вл ют |
рі ні |
ви |
о и |
до |
ладкості |
функцій, |
серед |
ки |
||||||||||||||||||||||||||
ро шукуєт с |
ро в' |
|
ок. |
|
о |
у |
ожна вважати, |
|
о варіаційна постановка до вол є ро ширити клас |
|||||||||||||||||||||||||||
припусти |
и |
функцій і, отже, використовувати не дуже |
ладкі, |
проте сил но локалі овані |
а исні |
|||||||||||||||||||||||||||||||
функці , кі є дуже ефективни |
и при реалі аці |
|
етоду |
ітца – |
|
етоду скінченни |
еле |
ентів. |
|
|||||||||||||||||||||||||||
о |
л не |
о |
|
астосуванн |
|
тако о під оду на прикладі ро ра унку |
а атопро оново |
статично |
||||||||||||||||||||||||||||
неви начувано |
|
алки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.10.1. Метод скінченних елементів у формі методу переміщень |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ба атопро онову суціл ну |
алку, |
ку |
авантажено рівно |
ірно ро поділени |
|
навантаженн |
||||||||||||||||||||||||||||||
рис. . |
,а , |
ожна ро |
л дати |
к сукупніст |
окре |
и |
стержнів, |
кі поєднуют с |
|
іж со ою на |
||||||||||||||||||||||||||
опора . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Повна потенціал на енер і |
|
i |
уд - |
ко о еле ента i |
складаєт с |
|
потенціал но |
енер і |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дефор |
аці Ui |
і ро оти |
|
овнішні |
сил Ai : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
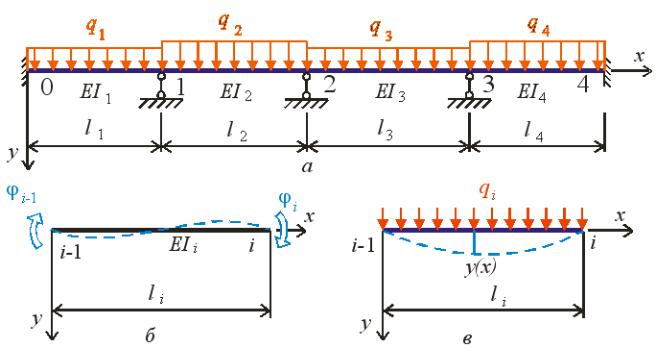
5. Енергетичні теореми і варіаційні принципи |
73 |
i Ui Ai . |
(5.158) |
|
|
|
|
|
|
|
|
|
|
|
|
ис. |
.20 |
|
|
|
|
|
|
|
|
|
|
|
||
Потенціал на енер і |
дефор |
аці |
Ui |
|
еле |
|
ента і ро ота |
|
овнішні сил Ai |
в ра і не туванн |
||||||||||||||||
поперечни и і по довжні |
и сила |
|
и |
ожут |
|
ути |
аписані |
к |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EIi |
li |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ui |
|
|
|
|
|
yi x |
dx , |
|
|
(5.159) |
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
li |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ai |
|
|
|
|
qi yi |
|
x dx , |
|
|
|
|
|
|
(5.160) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
відки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EIi |
|
li |
|
|
|
|
|
2 dx |
li |
|
|
|
|
|
|
|
||||
|
|
|
|
|
i |
|
|
|
y |
|
x |
|
q y |
i |
x dx. |
|
(5.161) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
Ба уючис |
на етоді |
ітца, представи |
|
о функцію про инів у ви л ді ку ічно о поліно |
а |
|||||||||||||||||||||
|
|
|
y |
i |
x |
a |
0 |
|
a x |
a |
2 |
x2 |
a |
3 |
x3 , |
|
(5.162) |
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
коефіцієнти |
ко о ожут |
ути ви начені |
|
|
ранични |
|
у |
ов рис.5.20, |
. ути |
повороту |
||||||||||||||||
ви начают с |
першою по ідною від функці про инів |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
i |
x |
y |
i |
x |
|
|
|
a |
|
|
2a |
2 |
x |
|
3a |
3 |
x2 . |
|
(5.163) |
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
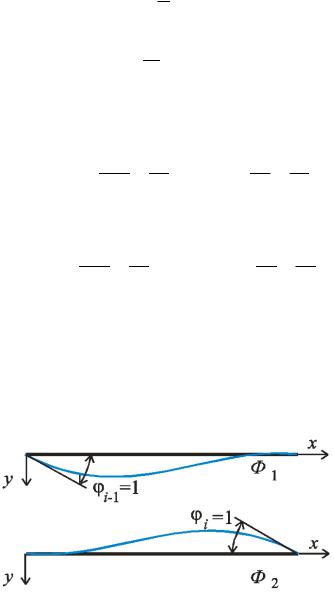
5. Енергетичні теореми і варіаційні принципи |
74 |
відси ає о
при x=0 |
yi |
0 |
|
a0 |
0; |
|
|
|
|
|
|
|
|
|||
|
|
|
i |
0 |
|
a1 |
i |
1; |
|
|
|
|
|
|
||
при |
x=l |
y |
|
l |
|
a |
a l |
|
a |
l2 |
|
a l3 =0; |
||||
|
|
|
i |
|
|
0 |
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
i |
l |
|
a |
2a l |
3a l2 |
|
. |
|||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
3 |
|
|
i |
|
о в авши рівн нн |
. |
4 , одержи о |
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
0; |
|
a |
1 |
2 |
i |
1 |
|
i |
; |
|||
|
|
0 |
|
|
|
|
2 |
li |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
; |
a |
1 |
|
|
|
. |
|
|
||
|
|
1 |
|
|
i 1 |
|
3 |
l2 |
|
i 1 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
Підстави о ро в ок |
. |
5 |
до |
|
. |
2 і |
веде |
о поді ні |
|
|
||||||
y x |
x 2x2 |
x3 |
|
i 1 |
x2 |
x3 |
. |
i |
l |
l2 |
|
l |
l2 |
i |
|
|
|
|
|
По начи о
(5.164)
(5.165)
(5.166)
|
|
|
x |
x |
2x2 |
x3 |
, |
|
x |
x2 |
x3 |
. |
(5.167) |
|
|
1 |
l |
l2 |
2 |
l |
l2 |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
ункці |
1 x і |
2 x |
на ивают с |
функці |
|
и фор |
и. Вони арактери уют |
про ини еле- |
|||||
ента відповідно від |
ушени |
кутів повороту |
|
1 і |
1. |
рафіки ци функцій наведено на |
|||||||
|
|
|
|
|
|
|
i 1 |
|
i |
|
|
|
|
рис. . 1.
|
ис. .21 |
|
Отже ура уванн по начен . |
про ини еле ента . |
на ерут ви л ду |

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
75 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
yi |
x |
i |
1 |
1 |
|
|
x |
i |
2 |
x |
|
|
|
|
|
|
|
|
(5.168) |
||||
а о в |
|
атричній фор |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
yi x |
|
|
Ф x |
i |
, |
|
|
|
|
|
|
|
|
|
|
|
(5.169) |
|||||
де Ф x |
|
1 |
x |
|
2 |
x |
|
атриц |
функцій фор |
и, |
|
i |
|
|
1 |
|
|
T |
вектор пере |
і |
ен |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
||||
кінців еле ента. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
піввідношенн |
. 8 |
дає |
о у вира ити повну потенціал ну енер ію еле |
ента |
5.161 чере |
||||||||||||||||||||||||||||
пере |
і енн |
|
йо о кінців. Отже, |
ожна |
аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
EI |
|
li |
d 2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
li |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
Ф |
|
Ф |
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
Ф |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
2 |
|
|
dx2 |
|
i 1 1 |
|
i |
2 |
|
|
|
|
|
|
|
i |
|
|
i 1 1 |
|
|
|
i |
2 |
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
EIi |
|
li |
Ф |
|
Ф |
|
2 |
|
|
|
|
|
li |
|
|
|
|
|
|
li |
Ф |
|
|
|
(5.170) |
||||||
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
q |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
i 1 1 |
|
i |
2 |
|
|
|
|
i |
|
i 1 |
|
1 |
|
|
|
|
i |
i |
|
2 |
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
Підставивши функці фор и . |
7 |
та |
ні дру і по ідні |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
4 |
|
6x |
|
|
|
|
|
x |
|
2 |
|
|
6x |
|
|
|
|
|
|
|
(5.171) |
||
|
|
|
|
|
|
|
|
1 |
l |
|
l2 |
|
|
2 |
|
|
|
l |
|
|
l2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
у . |
|
і виконавши інте руванн |
ура уванн |
|
|
|
то о, |
о |
|
величини кінцеви |
поворотів i 1 , |
i |
|||||||||||||||||||||
і інтенсивніст |
qi ро поділено о |
навантаженн |
є |
константа |
и, |
дістане |
о |
вира |
дл |
повно |
|||||||||||||||||||||||
потенціал но |
енер і |
еле |
ента |
к функці |
інни |
|
|
i |
1 і |
i : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2EIi |
2 |
|
1 |
|
i |
2 |
|
qili2 |
|
1 |
|
i |
. |
|
|
|
(5.172) |
|||||||
|
|
|
|
|
|
|
|
|
i |
li |
|
i 1 |
i |
|
|
i |
|
12 |
i |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Повна потенціал на енер і |
всіє |
|
а атопро оново |
алки |
рис. . |
,а |
|
|
ура уванн |
то о, |
о |
||||||||||||||||||||||
кути поворотів на відповідни |
кінц |
сусідні |
|
еле ентів однакові, |
оже |
ути аписана |
к су а |
||||||||||||||||||||||||||
енер ій усі |
|
окре и |
еле |
ентів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n |
|
n |
2EIi |
2 |
1 |
|
|
|
|
2 |
|
|
qili2 |
|
1 |
|
. |
|
(5.173) |
|||||||
|
|
|
|
|
|
|
|
i |
li |
i |
|
i |
|
1 i |
|
i |
|
|
12 |
i |
|
|
i |
|
|
|
|
||||||
|
|
|
|
|
|
i |
1 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
о в |
увал ні рівн нн дл ви наченн величин кутів повороту на опора |
алки одержи |
о, |
прирівн |
вши до нул частинні по ідні від повно потенціал но енер ій . |
3 по кожно |
у |

5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76 |
|||||||||||||||||||||||||||||||||
невідо и |
k |
|
k |
1,2,3 . Під час диференціюванн |
слід |
|
|
ати на ува і, |
о кут |
k , а ки |
|||||||||||||||||||||||||||||||||||||||||
дійснюєт с |
диференціюванн , |
в одит до дво |
|
сусідні |
|
|
еле ентів |
|
к поворот на право |
у кінці |
|||||||||||||||||||||||||||||||||||||||||
еле |
ента k і |
к поворот на ліво у кінці еле |
ента k+ . Отже, |
|
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2EI |
|
|
|
|
4EI |
|
|
4EI |
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
q l |
2 |
|
q l2 |
|
|
0; |
|
|
|
||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
l1 |
1 |
|
|
l2 |
|
2 |
|
|
|
|
l2 |
|
2 |
|
|
|
|
1 1 |
|
2 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
l1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
12 |
|
12 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2EI |
|
|
4EI |
|
|
|
4EI |
|
|
|
|
|
|
2EI |
|
|
|
|
|
q l |
2 |
q l |
2 |
|
0; |
|
|
(5.174) |
|||||||||||||||
|
|
|
|
|
2 |
l2 |
2 |
|
l2 |
2 |
|
|
|
l3 |
|
3 |
|
|
|
|
|
l3 |
|
3 |
|
|
|
2 |
2 |
3 3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
12 |
12 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2EI |
|
|
|
|
4EI |
|
|
|
4EI |
|
|
|
|
2EI |
|
|
|
|
|
q l |
2 |
q l |
2 |
|
0. |
|
|
|
|||||||||||||||
|
|
|
|
|
3 |
l3 |
3 |
|
|
l3 |
3 |
|
|
|
l4 |
|
4 |
|
|
|
l4 |
|
4 |
|
|
|
3 3 |
4 4 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
12 |
12 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Оскіл ки |
|
ранични |
|
у |
|
ов випливає, |
|
о |
|
0 4 |
|
|
0 , |
до оди |
|
о систе и тр о |
рівн н |
||||||||||||||||||||||||||||||||||
тр о |
а невідо и |
и 1, 2 , |
3 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4EI |
|
4EI |
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q l |
2 |
q |
l2 |
0; |
||||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
2 |
2 |
||||||
|
l1 |
|
|
|
l2 |
|
|
1 |
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2EI |
|
|
|
|
|
|
|
4EI |
|
|
4EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
q |
l2 |
q l2 |
0; |
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
2 |
3 3 |
|||||||
|
|
|
l2 |
|
1 |
|
|
|
|
|
|
l2 |
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
3 |
|
|
|
|
|
|
12 |
12 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4EI |
|
|
|
4EI |
|
|
|
|
|
q l2 |
q l2 |
0. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
3 |
4 |
4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
l4 |
|
|
|
|
|
3 |
|
12 |
12 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
і ичний |
|
|
іст |
кожно о |
ци |
|
рівн н |
|
|
|
|
|
це |
у |
|
ови |
|
рівнова и |
в |
ей, |
кі відповідно |
|||||||||||||||||||||||||||||
повертают с |
на кути 1, |
2 і |
3 . Отже коефіцієнти при невідо |
|
и |
|
і віл ні члени є реакці и у |
||||||||||||||||||||||||||||||||||||||||||||
відповідни в |
|
. |
атричній фор |
і о начені рівн нн |
|
|
ожут |
ути |
аписані у ви л ді |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
F |
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.175) |
|||||||
де K |
|
атриц |
|
жорсткості |
|
а атопро оново |
|
|
алки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4EI1 |
4EI2 |
|
|
|
|
|
2EI2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
l2 |
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2EI2 |
|
|
4EI2 |
|
|
4EI3 |
|
|
|
|
|
|
2EI3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
Κ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
l2 |
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2EI3 |
|
|
|
|
4EI3 |
|
|
4EI4 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
l4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
вектор невідо |
и кутів повороту |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
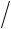
5. Енергетичні теореми і варіаційні принципи |
77 |
|
|
|
|
|
|
|
T |
|
|
|
2 |
|
|
|
; |
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|||
F |
вектор вантажни |
коефіцієнтів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
q l |
2 |
|
|
|
|
q |
2 |
l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
12 |
|
|
12 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
q2l22 |
|
|
|
q3l32 |
|
|
|
|||||||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
12 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
q l |
2 |
|
|
|
|
q |
4 |
l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
12 |
|
|
12 |
|
|
|
|
||||||
і нарешті, |
0 |
нул овий вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0T |
0 |
|
|
0 |
|
|
0 . |
|
|
|
||||
|
о в |
авши рівн нн . |
, дістане о вектор невідо |
и |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
K 1F , |
|
|
|
|
|
|
(5.176) |
||||||
післ |
чо о дл кожно о еле |
ента на |
а і співвідношенн |
5.168 |
оже о о числити |
инал ні |
||||||||||||||||
о |
енти і поперечні сили в уд - |
ко у перері і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Mi |
x |
EIi yi |
EIi |
i 1 |
|
1 |
x i 2 x |
|
(5.177) |
||||||||||
|
|
|
Qi |
x dMi |
x dx |
EIi |
i |
|
|
1 x i |
2 x . |
|||||||||||
|
|
|
1 |
|
|
|||||||||||||||||
5.10.2. Метод скінченних елементів у формі методу сил |
|
|
|
|||||||||||||||||||
|
о л не |
о попередню алку |
рис. |
. 0,а , вважаючи |
|
|
утвореною однопро онови |
статично |
||||||||||||||
ви начувани |
алок, |
до ки , окрі |
адано о |
овнішн о о навантаженн , прикладені о |
енти, о |
|||||||||||||||||
виникают |
у |
аданій |
алці над |
опора |
и рис. . |
2,а . |
|
|
|
|
|
|
|
|||||||||
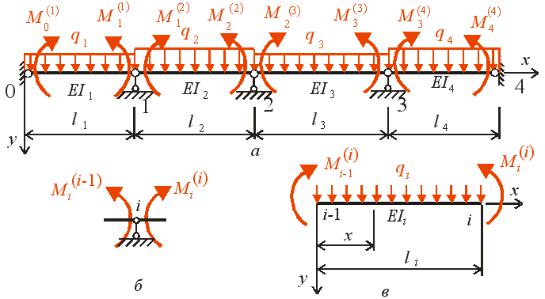
5. Енергетичні теореми і варіаційні принципи |
78 |
|
|
|
|
|
|
|
|
|
|
|
|
ис. .22 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
іл кіст |
не алежни |
|
пара |
етрів, |
о ви начают |
напружений стан |
а атопро оново алки, |
||||||||||||||||||||
дорівнює кіл кості |
инал ни |
о |
ентів над опора |
|
и. |
|
|
і пара |
етри |
ожна |
аписати у ви л ді век- |
|||||||||||||||||
тора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MT |
|
M0 |
M1 |
|
M2 |
|
|
|
M3 |
M4 . |
|
|
(5.178) |
||||||||
|
у |
ов рівнова и опорни ву лів випливає, |
о |
|
инал ні о |
енти, |
кі діют ліворуч і праворуч |
|||||||||||||||||||||
кожно опори |
рис. |
. , |
, дорівнюют |
один одно |
у |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
Mi(i) |
|
Mi(i |
1) |
|
|
|
Mi . |
|
|
|
|
(5.179) |
||||||||
|
о |
л не |
о уд - кий про ін |
алки рис. |
. 2,в . |
инал ний |
о |
ент в довіл но |
у перері і |
|||||||||||||||||||
а сцисою x |
оже |
ути |
аписаний у ви л ді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Mi |
x |
Mi 1 |
li |
|
x |
|
|
Mi |
|
|
x |
|
|
M p |
x , |
|
|
(5.180) |
||||
|
|
|
|
|
|
|
li |
|
|
li |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Mi |
1, Mi |
осереджені |
о |
енти на ліво |
у і право |
|
|
у кінц |
|
про ону, |
M p x |
инал ний |
||||||||||||||||
о |
ент у перері і від ді |
овнішн о о навантаженн в про оні. |
В ра і рівно ірно ро поділено о |
|||||||||||||||||||||||||
навантаженн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M p |
x |
qili2 |
|
|
x |
|
|
|
x2 |
. |
|
|
|
|
(5.181) |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
li |
|
|
li2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
апише о потенціал ну енер ію дефор аці
5. Енергетичні теореми і варіаційні принципи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
li |
|
Mi2 x |
|
|
|
|
|
|
1 |
li |
|
|
|
li |
|
x |
|
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Ui |
|
|
|
|
|
dx |
|
|
|
|
|
Mi |
1 |
|
|
Mi |
M p |
|
x |
dx . |
|
|
(5.182) |
|||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
2EIi |
|
|
|
2EIi |
0 |
|
li |
|
|
li |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Проінте рувавши |
|
співвідношенн |
|
. |
|
|
|
ура уванн |
|
|
то о, |
|
о |
кінцеві |
|
о |
енти є |
|||||||||||||||||||||||||||||
константа и, дістане о вира |
|
дл |
потенціал но |
енер і |
дефор |
аці |
|
однопро оново |
алки |
||||||||||||||||||||||||||||||||||||||
рис. . |
,в |
чере |
осереджені |
|
|
о енти на кінц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Ui |
|
li |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
qili3 |
|
|
|
|
|
|
|
qi2li5 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Mi 1 |
|
Mi |
1Mi |
Mi |
|
|
|
|
|
|
Mi 1 |
Mi |
|
|
|
|
|
|
. |
|
|
(5.183) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
6EIi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24EIi |
|
|
|
|
|
|
|
240EIi |
|
|
|
||||||||||||||
|
Потенціал на енер і |
а атопро оново |
алки |
це су |
|
а енер ій окре |
и |
про онів |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
n |
|
n |
|
|
|
li |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
qili3 |
|
Mi |
|
Mi |
|
|
qi2li5 |
|
|
|
||||||||||||
U |
|
|
Ui |
|
|
|
|
|
|
Mi |
1 |
|
|
Mi 1Mi |
Mi |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
(5.184) |
|||||||||||||||
|
|
|
|
6EIi |
|
|
|
|
|
24EIi |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
i |
1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
240EIi |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
де n |
кіл кіст про онів |
в дано |
у випадку n . |
а підставі теоре |
и |
астіл |
но див.п. . |
у ови |
|||||||||||||||||||||||||||||||||||||||
су існості дефор |
ацій у |
ісц |
|
стиковки |
ожут |
ути |
|
аписані чере |
перші частинні по ідні від |
||||||||||||||||||||||||||||||||||||||
повно |
|
потенціал но |
енер і по не алежни |
пара |
етра |
|
Mi |
|
i |
0,1,...,4 |
. |
|
ати е |
|
о на ува і, |
||||||||||||||||||||||||||||||||
о при диференціюванні |
а ци |
|
пара етро |
він в одити е в два доданки, |
о відповідают дво |
||||||||||||||||||||||||||||||||||||||||||
про она |
, |
кі при |
|
икают |
до опори i. Отже, дл |
довіл но о пара етра Mi |
ає |
о |
|
|
|
||||||||||||||||||||||||||||||||||||
|
Ui |
|
|
li |
|
Mi |
1 |
2Mi |
|
|
|
qili3 |
|
|
|
|
li 1 |
|
2Mi |
|
Mi |
1 |
|
qi 1li3 1 |
|
0. |
(5.185) |
||||||||||||||||||||
|
Mi |
|
6EIi |
|
|
24EIi |
|
6EIi |
1 |
|
|
|
|
24EIi |
1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
к о про они алки ают постійну жорсткіст EI=const , то співвідношенн . відо ий курсуопору атеріалів ви л д рівн нн тр о о ентів
li Mi 1 2 li |
|
li 1 Mi li 1M i 1 |
6Ri . |
|||
ут по начено |
|
|
|
|
|
|
R |
|
qili3 |
|
qi 1li3 1 |
. |
|
|
|
|
|
|||
i |
24 |
24 |
|
|
||
|
|
|
||||
Отже, аписавши співвідношенн . |
6 дл |
кожно опори, ати |
е о систе у ро в |
|||
рівн н
на уває
(5.186)
(5.187)
увал ни
5. Енергетичні теореми і варіаційні принципи |
80 |
2l1M0 |
|
l1M1 |
|
|
|
|
|
6R0; |
|
|
l1M0 |
|
2 l1 l2 M1 |
|
l2M2 |
|
|
|
6R1; |
(5.188) |
|
|
|
|
|
|
|
|
|
|
||
|
||||||||||
|
|
|
|
|
l4M3 |
|
2l4M4 |
6R4 |
|
|
стосовно инал ни |
о ентів у алці над |
опора |
и. |
|
|
|
|
|||

ДО ЗМІСТУ ПІДРУЧНИКА
ІІ. РОЗРАХУНОК СТЕРЖНЕВИХ СИСТЕМ
МЕТОДОМ СКІНЧЕННИХ ЕЛЕМЕНТІВ
6.Метод скінченних елементів y формі методу переміщень
7.Метод скінченних елементів y формі методу сил
Задачі опору матеріалів і будівельної механіки звичайно формулюються у вигляді диференціа-
льних рівнянь. Механічні або фізичні характеристики, такі, як переміщення, деформації, напру-
ження тощо, вважаються неперервними функціями координат. Фізичне тіло при цьому подумки уявляється сукупністю елементів нескінченно малих розмірів. З іншого боку, фізичне тіло можна розкласти на множину елементів скінченних розмірів і розглядати його як сукупність скінченних елементів. Такий підхід називають методом скінченних елементів (МСЕ). Зауважимо, що у сте-
ржневих системах за скінченні елементи беруться окремі стержні.
Перший етап розрахунку полягає в дискретизації, тобто в переході від розрахункової схеми стержневої н системи н до н її н скінченно-елементної н моделі. н Вихідна н розрахункова н схема н розбивається на окремі стержні (скінченні елементи) і вузли. В стержневих системах за скінченні елементи бе-
руться, як правило, прямолінійні стержні постійної жорсткості, на яких може бути розташоване рівномірно розподілене зовнішнє навантаження. Криволінійні стержні апроксимуються кількома прямолінійними елементами. Аналогічно апроксимуються стержні, що мають змінну жорсткість,
або ті, до яких прикладено нерівномірно розподілене навантаження. Така схема споруди нази-
вається її дискретною, або скінченно-елементною моделлю (СЕМ).
Вузлами нскінченно-елементної нмоделі нвважатимемо нточки нпоєднання ндвох набо нбільше нокремих стержнів, ступінчастої зміни жорсткості стержнів, прикладення зосереджених зовнішніх сил або моментів, ступінчастої зміни інтенсивності розподіленого навантаження, опорні вузли.
Розрізняють методи скінченних елементів у формі методу сил і у формі методу переміщень.
Під час виконання розрахунків за МСЕ у формі методу сил за основні невідомі, тобто ті, що обчи-
слюються в першу чергу, покладаються величини зусиль у стержнях системи. Ці величини, а та-
кож переміщення вузлів визначаються із розв’язання повної системи рівнянь будівельної механі-
ки. Метод скінченних елементів у формі методу переміщень маємо в тому разі, якщо за основні невідомі характеристики вузлів беремо їх поступальні та кутові переміщення. Саме такий підхід,
як правило, застосовують у практичних розрахунках.
О П А
6. озрахунок стержневих систем М Е у формі методу переміщень
Зміст глави
. |
. |
кінченно-еле ентна одел ро ра унково с е |
и стержнево систе и |
||||||||||||
. |
. |
інцеві |
арактеристики стержневи скінченни |
еле ентів |
|
||||||||||
. |
. |
атриц |
перетворенн |
|
|
|
|
|
|
|
|
|
|
||
. |
. По удова |
атриці жорсткості стержн |
в локал ній систе і координат |
|
|||||||||||
. |
. |
атриці жорсткості стержневи |
еле |
ентів у локал ній систе і координат |
|||||||||||
. |
. |
атриці жорсткості стержн в |
ло ал ній систе |
і координат |
|
||||||||||
. |
. Ву лові |
арактеристики скінченно-еле ентно |
оделі |
|
|||||||||||
. |
. |
атриц |
жорсткості скінченно-еле ентно оделі |
||||||||||||
. |
. Ви наченн |
усил у стержн |
|
|
|
|
|
|
|
|
|
|
|||
6.10. о ра унок плоско шарнірно-стержнево систе |
и |
етодо |
скінченни еле |
||||||
|
|
ентів |
|
|
|
|
|
|
|
6.11.Приклад ро ра унку ра и а етодо |
скінченни |
еле ентів |
|
||||||
6.12. Осо ливості ро ра унку просторови |
стержневи |
систе |
|
||||||
6.12. |
. |
івн нн |
рівнова и ву лів просторови ра |
|
|
|
|||
6.12. |
. |
атриц |
перетворенн |
|
|
|
|
||
6.13. |
|
атриц жорсткості просторово о стержн |
|
|
|
||||
6.14. Приклад ро ра унку просторово ра |
и етодо |
скінченни |
еле ентів |
||||||
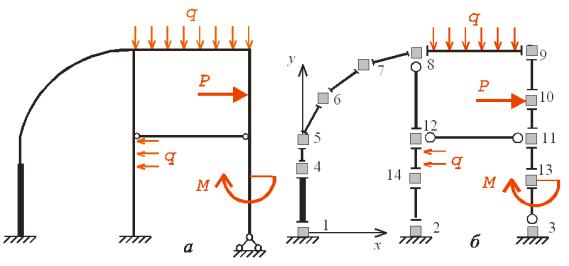
Е в ормі мето |
перемі ен |
2 |
6.1. кінченно-елементна модель розрахункової схеми стержневої системи
|
Перший етап ро ра унку пол |
ає в дискретизації, то то в пере оді від ро ра унково с е |
и |
||||||||||||||||||
стержнево |
систе |
и до |
скінченно-еле |
ентно |
оделі. Ви ідна ро ра ункова с е а ро |
иваєт с |
|||||||||||||||
на окре |
і стержні |
скінченні еле |
енти |
і ву ли. В стержневи |
систе |
а |
а скінченні еле |
енти |
е |
||||||||||||
рут с , |
к правило, |
пр |
олінійні стержні постійно жорсткості, на |
ки |
|
оже |
ути ро ташоване |
||||||||||||||
рівно ірно ро поділене |
овнішнє навантаженн . |
риволінійні стержні апрокси |
уют с |
кіл ко |
а |
||||||||||||||||
пр |
олінійни |
и еле |
ента |
и. Анало ічно апрокси уют с стержні, |
о |
ают |
інну жорсткіст , |
||||||||||||||
а о ті, |
до |
ки |
прикладено нерівно ірно ро поділене навантаженн . |
ака с е |
а споруди на и- |
||||||||||||||||
ваєт с |
дискретною, або скінченно-елементною моделлю |
ЕМ . |
|
|
|
|
|
|
|
|
|||||||||||
|
Ву ла |
и скінченно-еле |
ентно |
оделі вважати е о точки поєднанн |
дво |
а о |
іл ше окре |
||||||||||||||
и |
стержнів, |
ступінчасто |
іни жорсткості стержнів, прикладенн |
осереджени |
овнішні |
сил |
|||||||||||||||
а о |
о |
ентів, ступінчасто |
іни інтенсивності ро поділено о навантаженн , опорні ву ли. |
|
|
||||||||||||||||
|
Пере ід від ро ра унково с е |
и до скінченно-еле ентно |
оделі пока ано на рис. |
. . |
о ра |
||||||||||||||||
ункова с е а ра |
и |
рис. . ,а |
перетворена на дискретну |
одел |
рис. |
. , . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ис. . . |
|
|
|
|
|
Ву ли скінченно-еле ентно |
оделі у дано у прикладі прону еровані в довіл но у пор дку. |
||||||||||||
алі |
уде пока ано, |
о спосі ну |
ераці |
впливає на структуру систе |
и ро в |
увал ни |
рівн н . |
||||||
л |
ідентифікаці уд - |
ко о скінченно о еле |
ента достатн о вка ати но ери ву лів, кі він поєд |
||||||||||
нує. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
ви наченн |
в ає но о ро ташуванн |
ву лів, |
кіне атични |
і статични |
арактеристик |
||||||
вводит с |
а ал на дл |
всіє |
скінченно-еле ентно |
оделі систе а координат xy, |
ка на иваєт с |
||||||||
загальною, а о глобальною. |
|
|
|
|
|
|
|
|
|||||
Бе посередн о |
кожни |
стержне |
пов |
уєт с |
йо о власна систе а координат x’y’, кою |
||||||||
ручно користуватис |
адл |
аналі у напружено-дефор овано о стану стержн . |
ака систе |
а коор |
|||||||||
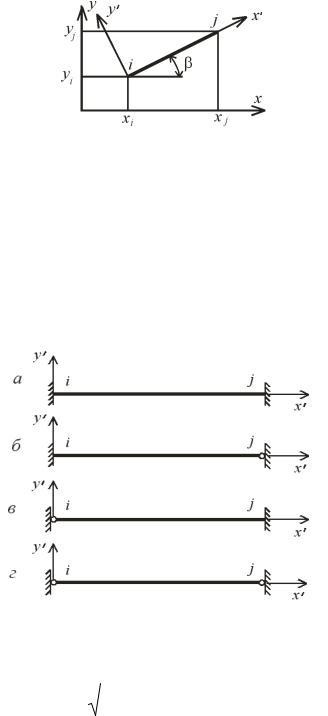
6. МСЕ в формі методу переміщень |
3 |
динат називається локальною. Початок локальної системи координат пов’язується з тим вузлом,
який має менший номер. Цю точку називають початком стержня, а точку, яка розташована на протилежному кінці стержня − його кінцем. Вісь x’ спрямовують вздовж стержня від його почат-
ку до кінця, а вісь y’ − перпендикулярно до стержня, причому прямий кут відкладається від осі x’
проти руху годинникової стрілки (рис.6.2). На рисунку початок стержня позначено літерою і, а кі-
нець − літерою j. Такі позначення застосовуватимуться надалі.
Рис.6.2
У плоскій дискретній моделі можливі чотири типи скінченних елементів, які розділяються між собою граничними умовами, тобто способами примикання до вузлів:
∙жорсткий вузол на початку і жорсткий вузол на кінці стержня (рис.6.3,а);
∙жорсткий вузол на початку і шарнірний вузол на кінці стержня (рис.6.3,б);
∙шарнірний вузол на початку і жорсткий вузол на кінці стержня (рис.6.3,в);
∙шарнірні вузли на початку і на кінці стержня (рис.6.3,г).
Рис.6.3
Довжина стержня обчислюється через координати вузлів на початку і на кінці за формулою:
l = |
|
, |
|
(x j − xi )2 + (y j − yi )2 |
(6.1) |
де xi , x j , yi , y j − координати відповідних вузлів у глобальній системі координат.

Е в ормі мето |
перемі ен |
4 |
ри оно етричні функці кута повороту локал но |
систе и координат стержн |
відносно |
ло ал но систе и координат усіє скінченно-еле ентно |
оделі о числюют с а фор |
ула и |
|
|
sin |
yj |
yi , cos |
xj |
xi . |
(6.2) |
|
|
|
l |
|
|
l |
|
6.2. Кінцеві характеристики стержневих скінченних елементів |
|
||||||
процесі дефор уванн |
споруди |
ву ли і, отже, кінці стержнів пере і уют с , внаслідок |
|||||
чо о на кінц |
виникают |
реакці в ає оді |
стержнів |
ву ла и скінченно-еле ентно |
оделі. |
||
О начені реакці |
і пере і енн ожут |
ути ви начені а о в |
ло ал ній, а о в локал ній систе і |
||||
координат. |
|
а рис. . ,а |
о ражено ко поненти пере і ен |
початку і кінц стержн , кі орієнто |
|||||||||||||
вані а ос |
|
и ло ал но |
систе |
и координат скінченно-еле |
ентно оделі. |
|
|
|
|||||||||
При ц о у пере і |
енн |
ну |
ерувати е о у стро о ви начено |
у пор дку, |
о наведено |
у |
|||||||||||
та л. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ут |
|
|
|
|
|
апр |
пере і енн |
|
В довж осі |
|
|
В довж осі y |
|
повороту |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а початку |
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
а кінці j |
|
|
4 |
|
|
|
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
аки |
чино |
, |
пере |
і енн |
початку стержн |
в ло ал ній систе |
і координат |
ожут ути |
а |
||||||||
писані у ви л ді |
атриці-стовпц |
вектора |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а о в транспонованій фор і
T |
1 |
2 |
3 |
. |
i |
||||
|
|
|
|
i |
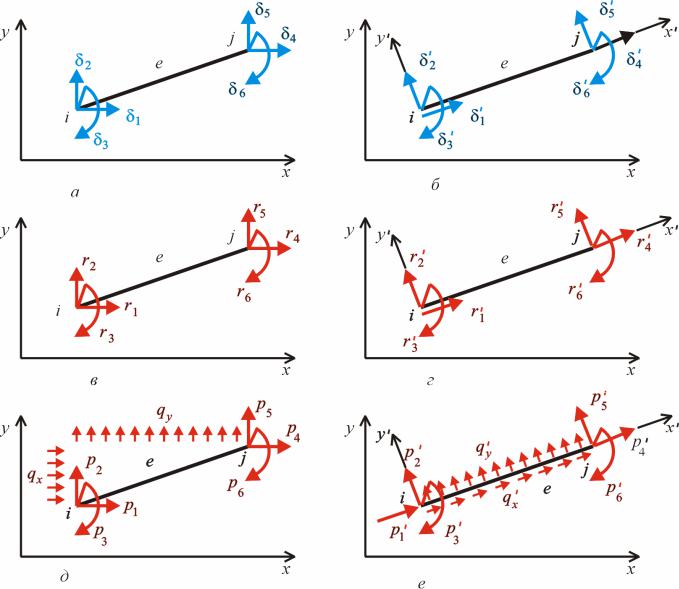
6. МСЕ в формі методу переміщень |
5 |
Рис.6.4
Аналогічно можна подати вектор переміщень кінця стержня:
|
δ4 |
|
|
|
|
|
|
|
|
= {δ4 |
δ5 δ6} . |
δ j |
= δ5 |
або |
δTj |
||
|
|
|
|
|
|
|
δ6 |
j |
|
|
|
Повний вектор кінцевих переміщень скінченного елемента в глобальній системі координат матиме в транспонованій формі наступний вигляд
δTe = {δi |
δ j } |
= {δ1 δ2 |
δ3 |
|
δ4 |
δ5 |
δ6 |
} |
|
||||||||
|
|
e |
|
|
|
|
|
e |
На рис.6.4,б,в зображено кінцеві реакції r, які зумовлені переміщеннями вузлів скінченноеле-
ментної моделі, а також кінцеві вантажні реакції (кінцеві сили) p, зумовлені дією розподілених в

6. МСЕ в формі методу переміщень |
6 |
межах стержня навантажень qx і q y . Нумерація компонентів кінцевих реакцій збігається з нуме-
рацією відповідних кінцевих переміщень. Означені кінцеві реакції також подано у вигляді векто-
рів
reT |
= {ri |
rj }e = {r1 r2 |
r3 |
r4 |
|
r5 |
r6}e , |
|
|
|
|
|
|
|
|
pTe = {pi |
pj }e = { p1 |
p2 |
p3 |
|
p4 |
p5 p6}e . |
|
|
|||||||
|
|||||||
Кінцеві переміщення і реакції також можуть бути подані у вигляді компонентів, які являють собою проекції відповідних величин на осі локальної системи координат (рис.6.4,г,д,е). Нумерація кінцевих реакцій також строго фіксована й аналогічна нумерації кінцевих переміщень в глобаль-
ній системі координат. Так, для кінцевих переміщень у локальній системі координат використо-
вують позначення, наведені у табл.6.2.
|
|
|
Таблиця 6.2 |
Напрям переміщення |
Вздовж осі х’ |
Вздовж осі y’ |
Кут |
повороту |
|||
|
|
|
|
На початку і |
δ′ |
δ′ |
δ′ |
|
1 |
2 |
3 |
|
|
|
|
На кінці j |
δ′ |
δ′ |
δ′ |
|
4 |
5 |
6 |
|
|
|
|
Так само нумеруються й кінцеві реакції.
Кінцеві переміщення і кінцеві реакції в локальній системі координат також можуть бути пред-
ставлені у вигляді векторів:
′T |
′ |
′ |
} |
|
′ |
|
′ |
|
′ |
|
|
|
′ |
′ |
|
′ |
} , |
||
|
|
|
|
||||||||||||||||
δe |
= {δi |
δ j |
|
= {δ1 |
δ2 |
δ3 |
|
|
δ4 |
δ5 |
|
δ6 |
|||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
} |
|
e |
|
|
′T |
′ |
′ |
|
|
|
′ |
′ |
′ |
|
′ |
|
′ |
′ |
, |
|
|
|||
|
|
|
|
|
|
||||||||||||||
re |
= {ri |
rj } |
|
|
= {r1 |
r2 |
r3 |
|
r4 |
|
r5 |
r6 |
|
|
|||||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
||
′T |
′ |
′ |
|
} |
′ |
|
′ |
|
′ |
|
′ |
|
′ |
|
′ |
} . |
|||
|
|
|
|
|
|
||||||||||||||
pe |
= {pi |
pj |
= { p1 |
|
p2 |
|
p3 |
|
p4 |
p5 |
|
p6 |
|||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
Розподілені на стержневому скінченному елементі. навантаження, можуть бути орієнтовані за
осями зглобальної зсистеми зкоординат звсієї зскінченно-елементної змоделі (рис.6.5,а) забо за зосями зло-
кальної системи координат даного елемента (рис.6.5,б).
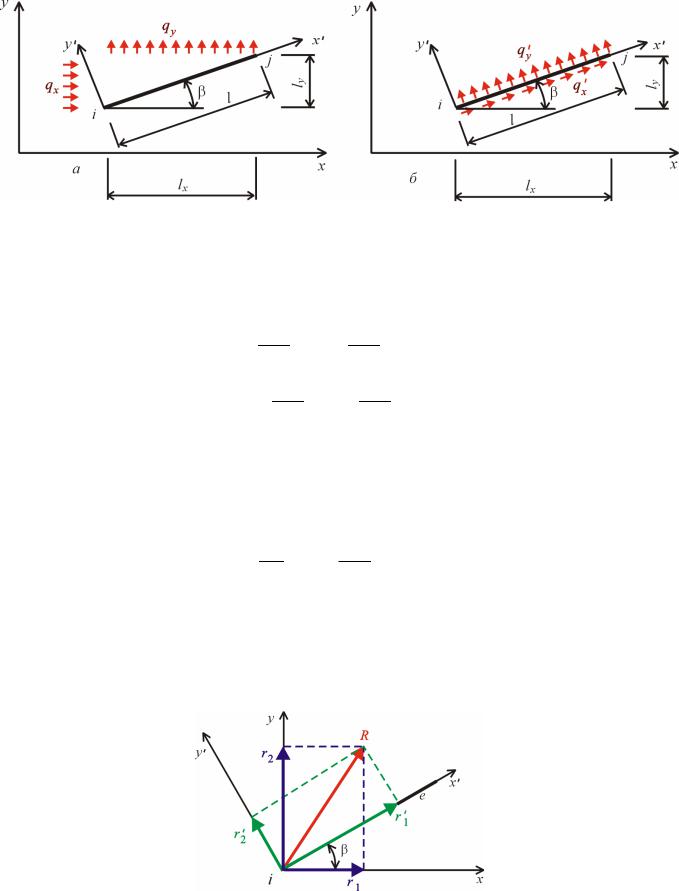
Е в ормі мето |
перемі ен |
7 |
ис. . |
|
авантаженн , орієнтоване по ло ал ни ос координат, |
оже ути перетворене у наван |
таженн , орієнтоване по локал ній систе і координат, а фор ула |
и |
q |
x |
qxly cos |
|
qylx sin ; |
||||
|
|
l |
|
|
l |
|
||
|
|
|
|
|
|
|||
q |
y |
|
qxly sin |
qylx cos . |
||||
|
|
|
|
l |
|
|
l |
|
|
|
|
|
|
|
|
||
л воротно о пере оду ожна скористатис |
|
співвідношенн и |
||||||
q |
|
q |
x |
l |
cos |
|
qyl |
sin ; |
x |
|
|
|
|
||||
|
ly |
|
|
|
ly |
|
||
|
|
|
|
|
|
|||
q |
|
q |
l |
sin |
qyly |
cos . |
||
y |
|
x |
|
|
|
|||
|
lx |
|
|
|
lx |
|
||
|
|
|
|
|
|
|||
6.3. Матриця перетворення
(6.3)
(6.4)
іж кінцеви |
и арактеристика и в ло ал ній і локал ній систе а координат існує певний |
в ок. о л не |
о, наприклад, початок i стержн e рис. . . |
ис. .
6. МСЕ в формі методу переміщень |
8 |
Вектор рівнодіючої R кінцевих реакцій розкладемо на дві складові за осями глобальної сис-
теми координат:
R = r1 + r2.
З іншого боку, ту саму рівнодіючу R можна розкласти на складові за осями локальної систе-
ми координат:
R = r′ + r′ .
1 2
Отже,
′ |
′ |
|
|
r1+ r2 |
= r |
1+ r 2 . |
|
Порівняємо проекції на осі x’ і y’ лівої і правої частин цієї рівності:
∑Fx′ ® r1¢ = r1 × cosβ + r2 × sinβ ,
∑Fy′ ® r2¢ = -r1 ×sinβ + r2 ×cosβ .
Очевидно, що величина кінцевого моменту від повороту координатних осей не залежить:
r3¢ = r3.
Залежності, що знайдено, можуть бути подані в матричній формі
r1¢¢r2r¢3
|
cosβ |
sinβ |
0 |
|
r |
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
= - sinβ |
cosβ |
0 |
|
|
|
|
|
|
|
|
× r |
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
0 |
1 |
|
r |
|
|
|
|
|
|
|
|
i |
|
3 |
|
i |
i |
|
|
|
|
|
|
|
||
або у вигляді:
де
|
|
ri′ = ti |
× ri , |
(6.5) |
|
cosβ |
sinβ |
0 |
|
|
|
|
|
|
ti = |
|
|
|
|
- sinβ |
cosβ |
0 . |
||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
1 i |
||
Аналогічну залежність запишемо для кінця j стержня

6. МСЕ в формі методу переміщень |
9 |
r′j = t j × r j , |
(6.6) |
Для обох кінців стержня e маємо:
|
|
|
′ |
|
|
|
|
|
(6.7) |
|
|
|
|
re = Te |
× re . |
|
|
|
|
||
У цьому співвідношенні r′, |
r – вектори кінцевих реакцій відповідно в локальній і в глоба- |
|||||||||
|
|
e |
e |
|
|
|
|
|
|
|
льній системах координат, |
Te – матриця перетворення. Вона має вигляд |
|
|
|
||||||
|
cosβ |
sinβ |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− sinβ |
cosβ |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
0 |
0 |
|
|
T |
= |
|
|
|
|
|
|
|
|
(6.8) |
e |
|
0 |
0 |
0 |
cosβ |
sinβ |
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
− sinβ |
cosβ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
e |
|
Матриця Te має такі властивості: |
|
|
|
|
|
|
|
|||
1) детермінант матриці дорівнює одиниці: DetTe = 1; |
|
|
|
|
|
|||||
2) обернена матриця збігається з транспонованою: T |
−1 = TT |
, тобто |
|
|
|
|||||
|
|
|
|
e |
e |
|
|
|
|
|
|
|
|
T ×TT |
= TT |
×T |
= E , |
|
|
(6.9) |
|
|
|
|
e e |
e |
e |
|
|
|
|
|
де E – одинична матриця.
Матриці, які мають вказані властивості, називаються ортогональними.
Залежності, аналогічні (6.7), мають місце також для кінцевих переміщень і вантажних реакцій:
′ |
|
(6.10) |
δe = Teδe , |
||
′ |
|
(6.11) |
pe = Tepe. |
||
6.4. Побудова матриці жорсткості стержня в локальній системі координат
Між кінцевими реакціями в стержні і кінцевими переміщеннями, які їх викликають, існує зв’язок. Для величин, що орієнтовані за осями локальної системи координат скінченного елемен-
та, цей зв’язок може визначатися співвідношеннями:

Е в ормі мето |
перемі ен |
10 |
r1 |
k11 1 |
k12 2 |
k13 3 |
k14 4 |
k15 5 |
k16 6 |
|
|
r2 |
k21 1 |
k22 2 |
k23 3 |
k24 4 |
k25 5 |
k26 6 |
|
|
r3 |
k31 1 |
k32 2 |
k33 3 |
k34 4 |
k35 5 |
k36 6 |
(6.12) |
|
r4 |
k41 1 |
k42 2 |
k43 3 |
k44 4 |
k45 5 |
k46 6 |
||
|
||||||||
r5 |
k51 1 |
k52 2 |
k53 3 |
k54 4 |
k55 5 |
k56 6 |
|
|
r6 |
k61 1 |
k62 2 |
k63 3 |
k64 4 |
k65 5 |
k66 6 |
|
а о в |
атричній фор і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
re |
ke δe , |
|
|
|
|
|
|
|
|
(6.13) |
||
де re , |
δe – вектори кінцеви |
реакцій і кінцеви |
пере |
і ен |
|
стержн |
в локал ній систе |
і коорди |
|||||||||||||
нат, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k11 |
k12 |
k13 |
|
k14 |
k15 |
|
k16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k21 |
k22 |
k23 |
|
k24 |
k25 |
|
k26 |
|
|
|
|
|
|
|
|
|
|
|
|
ke |
|
k31 |
k32 |
k33 |
|
k34 |
k35 |
|
k36 |
|
|
|
|
(6.14) |
|
|
|
|
|
|
|
|
k41 |
k42 |
k43 |
|
k44 |
k45 |
|
k46 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
k51 |
k52 |
k53 |
|
k54 |
k55 |
|
k56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k61 |
k62 |
k63 |
|
k64 |
k65 |
|
k66 e |
|
|
|
|
|
|
– атриц |
жорсткості стержн |
в локал ній систе |
і координат. |
|
|
|
|
|
|
||||||||||||
Буд - |
кий коефіцієнт |
атриці жорсткості kij |
вл є со ою кінцеву реакцію ri , |
у овлену кін |
|||||||||||||||||
цеви |
пере і |
енн |
j |
1, |
а у |
ови, |
о інші кінцеві пере |
і |
енн дорівнюют |
нулю. |
|
||||||||||
|
|
|
|
|
|
||||||||||||||||
снує кіл ка |
етодів по удови |
атриці жорсткості стержневи |
еле |
ентів. |
айпростіши є |
||||||||||||||||
під ід, |
при |
ко у коефіцієнти атриці ви начают |
і |
ро ра унку стержн |
на почер ове |
ушене |
|||||||||||||||
пере |
і |
енн |
йо о кінців. |
цією |
етою, наприклад, |
оже |
ути апропоновано |
етод початкови |
|||||||||||||
пара |
етрів. |
Однак, у складніши |
випадка , наприклад, дл |
стержн |
в триви |
ірно у просторі, |
|||||||||||||||
такий спосі |
використати практично не |
ожливо. |
а ал ний |
етод |
по удови |
атриц |
жорстко |
||||||||||||||
сті уд - |
ки |
еле |
ентів, в то |
у числі і дл |
стержн |
на пло |
ині, рунтуєт с на ро |
л ді функці |
|||||||||||||
онала повно |
потенціал но енер і |
та у |
ов йо о |
іні |
у у. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е в ормі мето |
перемі ен |
11 |
к |
о не тувати дефор |
аці |
и |
суву, |
ро ота внутрішні сил (6.2) дл стержн , о дефор у- |
|||||||||||||||||
єт с , |
ви начаєт с |
фор улою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
n |
li |
(N |
M )dx, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 i 1 0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де |
по довжн |
дефор |
аці , |
іна криви ни стержн . |
|
|
|
|
|
|
|
|||||||||||
В |
|
ежа стержнево о еле |
ента e ро |
л не |
о дію рівно |
ірно ро поділени навантажен |
інтен |
|||||||||||||||
сивністю qx і qy , |
кі орієнтовані |
відповідно у напр |
ку осей |
x' і y локал но |
систе и коорди |
|||||||||||||||||
нат скінченно о еле |
ента. Потенціал |
овнішні |
сил |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
qxu |
qyv dx. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Повна потенціал на енер і |
стержн |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
U |
|
A |
1 l |
N |
|
M dx |
l |
q |
u |
q |
y |
v dx. |
|
(6.15) |
|||
|
|
|
|
|
|
|
|
2 0 |
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
По довжні сили і |
инал ні о |
енти пов |
|
ані |
дефор |
аці |
|
и співвідношенн |
и |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
EA , |
|
|
|
|
|
|
|
(6.16) |
||
|
|
|
|
|
|
|
|
|
|
M |
|
EI |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а о в |
атричній фор |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
N |
|
D |
, |
|
|
|
|
|
|
|
(6.17) |
|
де NT |
N |
M , |
T |
|
|
|
вектори внутрішні |
усил і дефор ацій в стержні, |
D |
|||||||||||||
атриц |
пружни |
констант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
D |
|
EA |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
EI |
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ефор аці пов ані пере і енн и співвідношенн и
|
du |
, |
d 2v |
(6.18) |
|
dx |
|
dx2 |
|
а о у атричній фор і

Е в ормі мето |
перемі ен |
12 |
|
|
|
|
|
|
d u. |
|
|
|
|
(6.19) |
|
ут по начено uT u v |
вектор пере |
і ен |
довіл но |
точки осі стержн , d атриц |
||||||||
диференціюванн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
d |
|
dx |
|
|
|
|
||||
|
|
|
|
|
2 . |
|
|
|
||||
|
|
|
|
|
|
d |
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dx2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
оді |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 l T |
|
1 l |
|
|
T |
|
|
||||
U |
2 |
|
Ndx |
2 |
0 |
d u |
|
Ddu dx, |
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Al uT qdx,
0
де |
qT |
qx |
qy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Отже, повна потенціал на енер і дефор |
аці виражаєт с |
співвідношенн |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 l |
|
|
T |
|
|
|
|
|
|
l T |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
Ddu dx |
|
u q dx. |
|
|
|
|
(6.20) |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
о |
понента |
и вектора u є по довжні і поперечні пере |
і |
енн |
довіл но о перері у стержн , |
||||||||||||||||||||||||
дл |
ви наченн |
|
ки |
досит |
складно по удувати аналітичні |
алежності. |
о |
у використає |
о полі |
|||||||||||||||||||||
но |
ну апрокси |
ацію пере |
і ен у |
|
ежа |
стержн , використавши властивості |
неперервності |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
2 |
x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.21) |
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
x |
|
x2 |
|
|
x3 . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
3 |
|
4 |
5 |
6 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
а начи |
о, |
|
о поліно |
и . |
є точни |
и ро в |
ка |
и однорідни |
диференціал ни |
рівн н |
|||||||||||||||||||
по довжні |
дефор ацій і поперечно о |
|
ину. |
|
о |
|
у о численн |
повно потенціал но |
енер і даст |
|||||||||||||||||||||
точний ре ул тат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ра овуючи те, |
о координата |
|
кінців скінченно о еле |
ента у співвідношенн |
. |
відпо |
|||||||||||||||||||||||
відают |
наченн |
ву лови |
пере і |
ен , |
складе |
о систе |
|
у шіст о |
лінійни |
ал е ра чни |
рівн н |
|||||||||||||||||||
відносно невідо |
и |
коефіцієнтів поліно |
ів. |
о в |
|
авши цю систе у, отри ає |
о наченн |
коефіці |
||||||||||||||||||||||
Е в ормі мето |
перемі ен |
13 |
єнтів, |
виражені чере |
ву лові пере і |
енн . |
арешті, підставивши одержані коефіцієнти в . , |
|||
ати |
е о пере і енн |
u і v уд - ко |
точки стержн |
у тако |
у ви л ді |
|
|
|
|
u |
1 1 |
4 4 |
; |
|
(6.22) |
|
|
v |
2 2 |
3 3 |
5 5 |
6 6 . |
|
|
|
|
|||||
ункці |
i , о в од т |
до співвідношен |
. |
о еле ента. |
атрично у |
аписі алежності . |
|
|
u |
1 0 |
0 |
|
u |
0 |
|
|
|
|
v |
2 |
3 |
|
|
|
|
||
, на ивают с функціями форми скінченно
ати ут такий ви л д
|
|
|
/ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
/ |
|
|
|
|
|
|
2 |
/ |
|
|
4 0 |
0 |
3/ |
. |
(6.23) |
||
0 |
|
|
/ |
δ |
||
5 |
6 |
|
|
|
||
|
4 |
|
|
|
||
5/6/
Повна потенціал на енер і . |
|
|
ура уванн |
|
. |
апишет с |
так |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 l |
|
|
T |
|
|
|
l |
|
|
T |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
δ |
|
|
Dd |
δ dx |
|
|
δ |
q dx. |
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
к о по начити |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
1 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
d 4 |
|
|
|
0 |
0 |
|
|
|||
B |
d |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
, |
||||||||
|
|
|
d 2 |
|
|
|
d 2 3 |
|
|
|
|
d 2 5 |
|
d 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
2 |
|
|
|
0 |
|
|
|
6 |
|
||||||||||||
|
|
|
|
|
|
|
dx2 |
|
|
|
dx2 |
|
|
|
dx2 |
|
dx2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
то фор ула дл |
о численн |
|
потенціал но енер і на уде ви л ду |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 l |
|
|
T |
|
|
|
|
|
l |
|
T |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Bδ |
|
|
DBδ dx |
|
|
δ q dx. |
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
Виконавши операцію транспонуванн , остаточно |
на оди |
о |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
1 l |
T |
|
|
T |
|
|
|
|
l |
|
T T |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
δ |
B |
|
DBδ dx |
δ |
|
|
q dx. |
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
(6.24)
(6.25)
(6.26)

Е в ормі мето |
перемі ен |
14 |
|
|
|
|
|
d |
|
|
|
l |
|
T |
|
|
|
l |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
DBδ dx |
|
|
q dx |
0. |
|
(6.27) |
|||
|
|
|
|
|
dδ T |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
аючи на ува і те, |
о вектор δ |
кінцеви |
пере |
і |
ен |
не |
алежит |
від координати x, апише |
||||||||||||
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
B |
T |
|
|
|
|
|
l |
T |
|
|
|
|
(6.28) |
|
|
|
|
|
|
|
|
DBdx δ |
|
|
qdx |
0, |
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
BT DBdx, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
(6.29) |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
qdx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Ви од чи |
то о, |
о вектор кінцеви пере |
і |
ен |
|
0 , ає о |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
k δ |
|
p |
0. |
|
|
|
|
(6.30) |
|||
ут k |
атриц жорсткості стержнево о скінченно о еле |
ента в локал ній |
систе |
і коорди |
||||||||||||||||
нат . |
, p |
вектор кінцеви |
вантажни |
реакцій, |
у |
овлени |
дією ро поділени |
навантажен у |
||||||||||||
ежа |
стержн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Буд - кий еле ент |
атриці жорсткості |
k |
і |
вектора кінцеви сил p ви начают с |
алежно |
|||||||||||||||
ст и, |
о випливают |
. і |
ают |
такий ви л д |
|
|
|
|
|
|
|
|||||||||
|
l |
d |
i |
d j |
|
|
|
EA |
dx |
|
dx |
dx |
|
при |
|
kij |
0 |
|
|
|
|
|
|
l |
d 2 |
|
d 2 |
|
|
|
|
EI |
i |
j |
dx |
при |
|||
0 |
dx |
2 |
dx |
2 |
|||
i, j 1,4 ,
i, j 2,3,5,6 .
(6.31)
p/ |
l |
q |
i |
dx |
при i |
, |
, |
0 |
1 |
|
|
|
|
||
i |
l q |
|
dx |
|
|
|
|
|
i |
(при i |
, |
, , . |
|||
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|

Е в ормі мето |
перемі ен |
15 |
6.5. Матриці жорсткості стержневих елементів у локальній системі координат
користає ос викладеною етодикою дл по удови атриц жорсткості стержневи еле ен
тів а рі ни ранични у |
ов. |
6.5.1. |
тержень із затисненнями на обох кінцях рис.6.7) |
ис. .
ає о такі раничні у ови
при
при
x=0 |
u |
0 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
3 |
2 ; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
dy |
0 |
|
|
|
|
4 |
|
|
3 |
. |
|
|
|
|
|||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x=l |
u |
l |
|
|
|
|
l |
|
|
; |
|
|
|
|
|
|
|||
|
|
|
1 |
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
|
y l |
|
3 |
|
4 |
l |
|
|
|
l2 |
l3 |
; |
|
||||||
|
|
|
|
|
|
|
|
5 |
|
|
6 |
|
5 |
|
|
||||
|
l |
dy l |
|
|
|
|
4 |
|
|
2 |
l |
|
3 |
l2 |
|
. |
|||
|
|
|
|
dx |
|
|
|
|
|
|
|
5 |
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о в уючи одержані рівн нн , на оди о
|
|
; |
|
4 |
|
3 |
; |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|||
|
2 |
4 |
1 ; |
5 |
3 2 |
2 3 |
3 5 |
l 6 ; |
|||
|
|
l |
|
|
|
|
l2 |
|
|||
|
3 |
|
; |
|
2 2 |
|
l 3 |
2 5 |
l 6 . |
||
|
2 |
|
|
6 |
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Підставивши одержані величини у (6.21) отри ає о функці фор и
1 |
1 |
x l; |
4 |
x l; |
|
|
2 |
1 |
3x2 l2; |
5 |
3x2 l2 |
2x3 l3; |
(6.32) |
3 |
|
x 2x2 l x3 l2; |
6 |
x2 l |
x3 l2. |
|
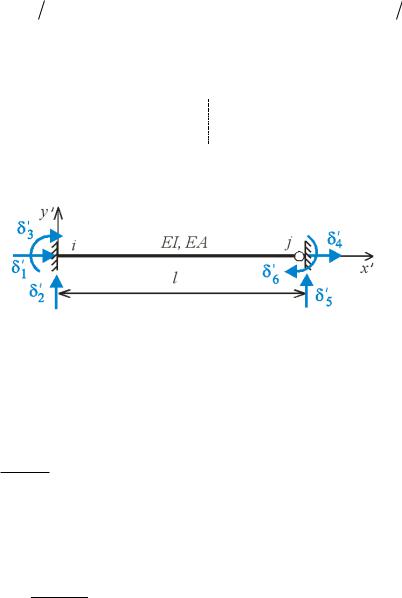
Е в |
ормі мето |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
||||||||||||||
|
|
|
f |
|
0 |
|
|
|
0 |
|
|
f |
0 |
|
|
|
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
12i |
|
|
6i |
0 |
|
|
12i |
|
|
6i |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
l2 |
|
|
l |
|
|
|
l2 |
|
|
l |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
0 |
|
|
|
|
6i |
|
4i |
0 |
|
|
6i |
|
2i |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
ke |
|
|
|
|
l |
|
|
|
l |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f |
0 |
|
|
|
0 |
|
|
f |
0 |
|
|
|
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
0 |
|
|
12i |
|
6i |
0 |
12i |
|
6i |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
l2 |
|
l |
|
l2 |
|
l |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0 |
|
|
|
|
6i |
|
2i |
0 |
|
|
6i |
|
4i |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ут по начено i |
EI l |
по онна жорсткіст |
стержн |
на |
ин, |
f EA l по онна жорст |
|||||||||||||||||||||||||
кіст стержн |
на по довжні дефор |
аці . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вектор вантажни |
реакцій при ц о у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
T |
|
|
qxl |
|
|
|
qyl |
qyl2 |
qxl |
qy |
|
|
|
|
qyl2 . |
|||||||||||||||
|
pe |
|
|
2 |
2 |
|
12 |
|
2 |
2 |
l |
12 |
|
|
|
|
|||||||||||||||
e
6.5.2. тержень із затисненням на початку і шарніром на кінці рис.6.
|
|
|
|
|
|
ис. . |
раничні у ови |
|
|
|
|
|
|
При x=0 u(0) |
|
/ |
; |
|
|
|
|
1 |
1 |
|
|
|
|
y 0 |
2 |
2 ; |
|
|
|
|
0 |
dy |
0 |
|
4 |
|
. |
|
dx |
|
3 |
|
||
|
|
|
|
|
||
При x=l u |
l |
|
|
|
l |
|
; |
|
|
|
|
|
|
||
|
|
1 |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
y l |
|
3 |
|
|
l |
|
|
l2 |
|
l3 |
|
|
; |
|
|
|
|
|
4 |
|
5 |
|
6 |
|
|
5 |
|
|
|||
M |
l |
EI |
d 2 y |
l |
|
EI |
2 |
|
6 |
l 0. |
|||||
dx2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
6 |
|
|||

Е в ормі мето |
перемі ен |
16 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
4 |
|
|
|
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
4 |
1 ; |
5 |
|
|
3 2 |
|
|
2 3 |
|
3 5 |
l 6 ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
3 |
|
2 |
; |
|
|
|
|
|
|
|
6 |
|
2 2 |
|
|
l 3 |
2 5 |
l 6 . |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Підставивши одержані величини у (6.21) отри |
|
ає |
о функці фор |
|
и |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
x l; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
x l; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
1 |
|
|
3x2 |
l2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
3x2 l2 |
|
2x3 l3; |
|
(6.32) |
|||||||||||||||||||||
|
|
|
|
3 |
|
|
|
x 2x2 l x3 l2; |
|
|
|
|
|
|
6 |
|
x2 l |
|
|
|
x3 l2. |
|
|
|
|
|
|
|||||||||||||||||||||||
епер, |
аючи |
наченн |
функцій фор |
|
и, |
а фор |
ула и |
(6.31), |
|
оже |
о |
|
найти еле енти |
ат |
||||||||||||||||||||||||||||||||||||
риці жорсткості стержн |
і еле |
|
енти вектора вантажни |
реакцій. О числи |
о, наприклад, еле енти |
|||||||||||||||||||||||||||||||||||||||||||||
k23 і p2 . Відповідно до |
начен |
|
|
індексів |
|
|
|
i=2, j= |
|
|
|
дл |
о численн |
|
еле |
ента k23 |
скористає |
ос |
||||||||||||||||||||||||||||||||
дру ою фор |
улою |
і співвідношен |
. . |
|
|
|
ру і по ідні функцій фор и |
2 |
|
і |
3 |
встановлює о |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рівн н |
. 2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 1 |
|
|
|
|
|
|
|
6 |
|
12x |
, |
|
|
|
|
d 2 3 |
|
= |
6 |
|
12x |
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
l2 |
|
|
l3 |
|
|
|
|
|
|
|
dx2 |
|
l2 |
|
l3 |
|
|
|
|
|
|
|
|||||||||||||||
відси |
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
d 2 |
2 |
|
|
|
d 2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k23 |
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dx 2 |
|
|
dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
6 |
|
|
|
12x |
|
6 |
|
12x |
|
|
|
12EI |
|
|
|
12i |
|
|
|
|
|
||||||||||||||||
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
.. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
l2 |
|
|
l3 |
|
|
|
|
l2 |
|
|
|
l3 |
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
о численн |
еле |
ента |
|
p2 |
скористає |
ос дру ою фор улою |
|
і співвідношен (6.31) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
p2/ |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
qy (1 3x2 l2 2x3 l3)dx |
|
qyl |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
qy 2dx |
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Анало ічно о числюют усі інші еле енти атриці жорсткості і вектора вантажни реакцій.
аводи о повну атрицю жорсткості k і вектор вантажни реакцій p дл стержнево о еле ен та, о ає атисненн о о кінців
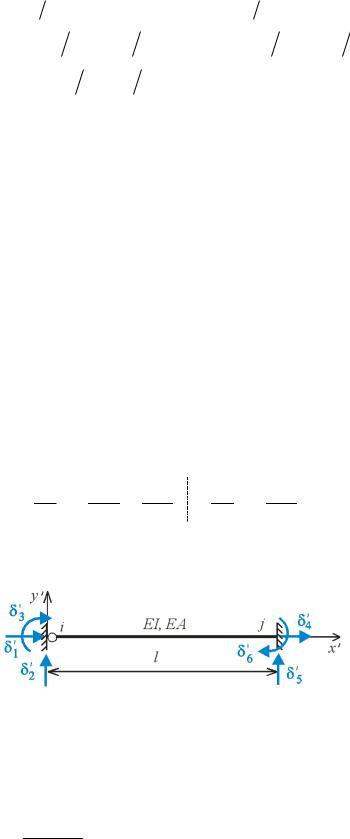
Е в ормі мето |
перемі ен |
18 |
о в авши ці рівн нн і підставивши одержані величини коефіцієнтів у (6.21), відшукує о функці фор и
1 |
1 x l; |
|
|
|
|
|
|
|
|
|
|
4 |
x l; |
|
|
||||||||
2 1 3x2 2l2 x3 2l3; |
|
5 3x2 2l2 x3 2l3; |
|||||||||||||||||||||
3 |
x 3x2 2l x3 2l2; |
6 |
0. |
|
|
|
|
|
|
|
|
||||||||||||
а фор ула и (6.31) |
на оди |
о коефіцієнти |
атриці жорсткості і еле енти вектора вантажни |
||||||||||||||||||||
реакцій |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
0 |
|
|
0 |
|
|
f |
0 |
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
3i |
|
|
3i |
|
0 |
|
|
|
3i |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
l2 |
|
|
l |
|
|
|
l2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
3i |
|
3i |
|
0 |
|
|
3i |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
l |
|
|
l |
, |
|||||||||||||||
ke |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f |
0 |
|
|
0 |
|
|
f |
0 |
|
|
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
3i |
|
3i |
|
0 |
|
|
3i |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
l2 |
|
l |
|
l2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
0 |
|
|
0 |
|
|
0 |
0 |
|
|
|
0 |
|
|||||||||
T |
|
qxl |
5qyl |
qyl2 |
|
qxl |
|
|
3qyl |
|
e |
||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
0 |
. |
||||||||||||||||||
pe |
2 |
8 |
|
|
8 |
|
2 |
8 |
|
|
|||||||||||||
e
6.5.3. тержень із шарніром на початку і з затисненням на кінці рис.6.9
ис. .
раничні у ови
При x=0 u |
0 |
|
; |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
y |
0 |
3 |
2 ; |
|
|
|
|
|
M |
0 |
EI |
d 2 y 0 |
EI |
2 |
|
0. |
|
dx2 |
5 |
|||||||
|
|
|
|
|
|
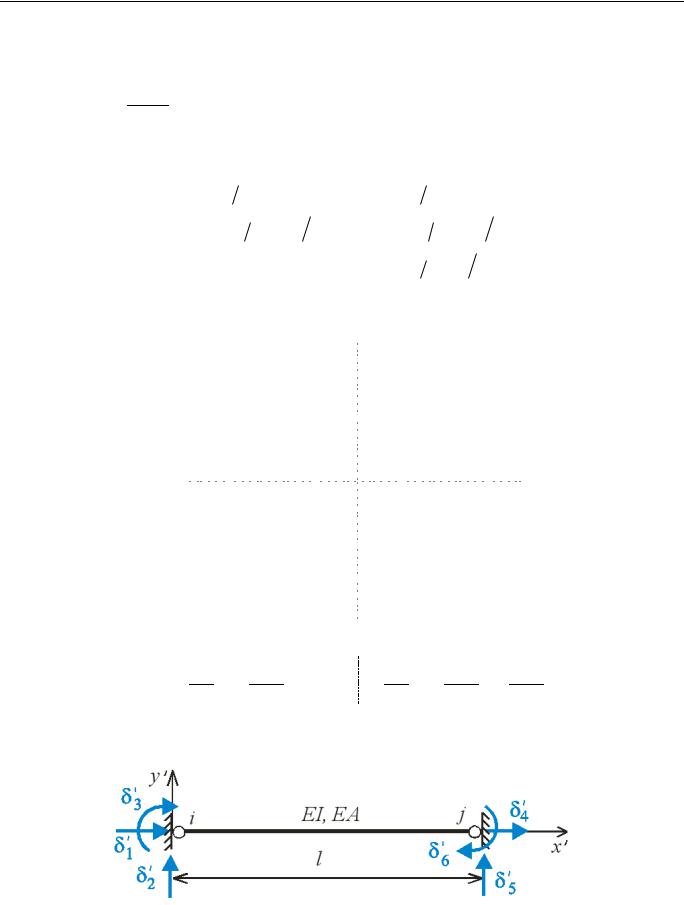
Е в ормі мето перемі ен 19
При x=l |
u l |
|
|
|
|
l |
|
|
4 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y l |
|
3 |
|
4 |
l |
|
|
|
l2 |
|
|
l3 |
|
5 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(l) dy(l) |
4 |
|
2 |
l |
3 |
l2 |
|
/ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dx |
|
|
|
|
|
|
|
5 |
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
о в |
авши наведені рівн нн , |
на оди |
о |
|
а допо |
о ою співвідношен (6.21) функці фор и |
||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
x l; |
|
|
|
|
|
|
|
|
|
4 |
x l; |
|
|
|
|
|
|||||||||
|
|
|
|
2 1 3x 2l x3 2l3; |
5 3x 2l x3 2l3; |
|
||||||||||||||||||||||||||||
|
|
|
|
3 0; |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
x l x3 2l2. |
|
|||||||||||||||
атриц жорсткості і вектор вантажни |
реакцій стержн |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
f |
|
|
|
0 |
|
|
|
0 |
|
f |
0 |
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
3i |
|
|
0 |
|
0 |
|
|
|
3i |
|
3i |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
l2 |
|
l |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
0 |
0 |
|
|
|
0 |
|
|
|
||||||||
|
|
ke |
|
|
|
|
|
f |
|
|
|
0 |
|
|
|
0 |
|
f |
0 |
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
3i |
|
|
0 |
|
0 |
|
|
3i |
3i |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
l2 |
l |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
3i |
|
|
0 |
|
0 |
|
|
3i |
3i |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
qxl |
|
|
3qyl |
|
|
0 |
|
qxl |
|
|
5qyl |
|
qyl2 |
. |
|||||||||||||
|
|
pe |
|
|
|
|
|
2 |
|
|
|
8 |
|
|
|
|
2 |
8 |
8 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.5.4. |
|
тержень із шарнірами з обох сторін рис.6.10 |
|
||||||||||||||||||||||||||||
ис. .
Е в ормі мето |
перемі ен |
20 |
раничні у ови
При x=0 u |
0 |
y |
0 |
M 0
|
; |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
3 |
2 ; |
|
|
|
|
|
EI |
d 2 y 0 |
EI |
2 |
|
0. |
|
dx2 |
5 |
|||||
|
|
|
|
При x=l |
u l |
|
|
|
|
l |
|
4 |
; |
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y l |
|
|
3 |
|
|
l |
|
|
l2 |
|
l3 |
|
|
5 |
; |
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
6 |
|
|
|
|
|
|
|
||||
|
M |
l |
EI |
d 2 y |
l |
|
|
EI 2 |
|
6 |
l |
0. |
|
|||||||
|
dx2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
6 |
|
|
|
||||
ункці фор |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 x l; |
|
|
4 |
x l ; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
x l ; |
|
|
5 |
x l; |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0; |
|
|
|
|
6 |
0. |
|
|
атриц |
жорсткості стержн і вектор вантажни |
реакцій |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
|
|
0 |
|
|
0 |
|
|
f |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
0 |
|
|
|
|
|
ke |
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
f |
|
|
|
0 |
|
|
0 |
|
|
f |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
0 |
|
|
|
|
T |
|
|
|
qxl |
|
|
qyl |
|
0 |
|
qxl |
qyl |
|||||
|
|
|
pe |
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0
0
0
0
0
0 e
0 .
e
6.6. Матриці жорсткості стержня в глобальній системі координат
атриці жорсткості стержн |
в локал ни |
систе |
а координат ви начают |
величини кінцеви |
||||
реакцій, кі орієнтовані |
а ос и локал ни систе координат. При ро |
л ді су |
арно ді |
стержнів |
||||
на ву ли скінченно-еле |
ентно |
оделі виникає нео |
ідніст привести всі ці реакці , |
о переда |
||||
ют с на ву ли |
оку стержнів, |
до спіл ни |
напр |
ів. а ці напр |
и доціл но о рати напр и |
|||
Е в ормі мето |
перемі ен |
21 |
осей |
ло ал но |
систе |
и координат всіє |
оделі. Отже, |
постає адача перетворенн кінцеви реак |
||||||||||||||||||||
цій стержн |
локал но |
у |
ло ал ну систе |
|
у координат, то то |
адача по удови |
атриц |
жорстко |
|||||||||||||||||
сті стержнів у |
ло ал ній систе і координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
к відо |
о, |
|
іж кінцеви и реакці |
и і кінцеви |
|
|
и пере і енн |
и стержн в локал ній систе |
і |
|||||||||||||||
координат існує |
алежніст |
(6.13): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
re keδe. |
|
|
|
|
|
|
|
|
|||||
|
іншо о |
оку, |
кінцеві величини в локал ній і |
|
ло ал ній систе а |
координат пов |
ані ат |
||||||||||||||||||
рицею перетворенн |
Te . |
к |
о вира ити в |
|
. |
кінцеві реакці |
re |
і кінцеві пере і енн δe , |
кі |
||||||||||||||||
спр |
овані |
а ос |
и локал но |
систе |
и координат, чере |
|
анало ічні величини в |
ло ал ній систе |
і |
||||||||||||||||
ідно |
6.7 |
і |
6.10 , одержи |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Te re ke Te δe . |
|
|
|
|
|
|
|||||||||
По |
ноживши ліворуч о идві частини рівності на о ернену |
атрицю перетворен , і |
важаючи |
||||||||||||||||||||||
на те, |
|
о о ернена |
атриц |
перетворен |
і аєт с |
|
|
транспонованою, |
оже о аписати |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
TT k |
e |
T δ |
e |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
e |
|
|
e |
|
e |
|
|
|
|
|
|
|
|||
По начивши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
k |
e |
|
TT k |
T , |
|
|
|
|
(6.33) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
e e |
|
|
|
|
|
|
|
|
|
врешті |
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
re |
|
keδe. |
|
|
|
|
|
|
(6.34) |
||||||
Матриця ke , що перетворює вектор кінцевих переміщень δe у вектор кінцевих реакцій у глобальній системі координат re , являє собою матрицю жорсткості у глобальній системі координат.
атричний вира . оже ути представлений співвідношенн и
r |
k |
k |
2 |
k |
3 |
k |
4 |
k |
5 |
k |
6 |
|
||||||||||
1 |
11 |
1 |
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
|
|||||||||
r |
k |
k |
22 |
|
2 |
k |
|
3 |
k |
24 |
|
4 |
k |
25 |
|
5 |
k |
26 |
|
6 |
|
|
2 |
21 |
1 |
|
|
23 |
|
|
|
|
|
|
|
||||||||||
r |
k |
k |
32 |
2 |
k |
|
3 |
k |
34 |
4 |
k |
35 |
5 |
k |
36 |
6 |
|
|||||
3 |
31 |
1 |
|
|
33 |
|
|
|
|
|
|
|
(6.35) |
|||||||||
r |
k |
k |
|
|
|
k |
|
|
k |
|
|
|
k |
|
|
|
k |
|
|
|
||
42 |
2 |
3 |
44 |
4 |
45 |
5 |
46 |
6 |
|
|||||||||||||
4 |
41 |
1 |
|
|
43 |
|
|
|
|
|
|
|
||||||||||
r |
k |
k |
52 |
2 |
k |
|
3 |
k |
54 |
4 |
k |
55 |
5 |
k |
56 |
6 |
|
|||||
5 |
51 |
1 |
|
|
53 |
|
|
|
|
|
|
|
|
|||||||||
r |
k |
k |
62 |
2 |
k |
3 |
k |
64 |
4 |
k |
65 |
5 |
k |
66 |
6 |
|
||||||
6 |
61 |
1 |
|
|
63 |
|
|
|
|
|
|
|
||||||||||
аки чино , атриц |
жорсткості стержн |
в |
ло ал ній |
|
а ал ній систе і координат ає ви |
|||||||||||||||||
л д
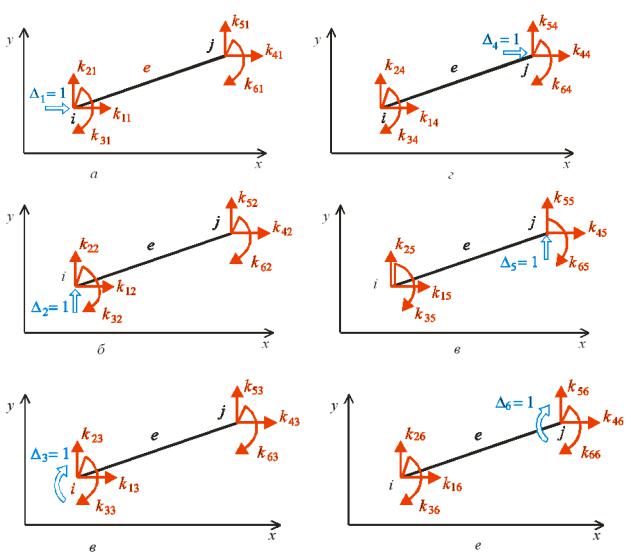
Е в ормі мето |
перемі ен |
22 |
цеві реакці , так і кінцеві пере |
і енн орієнтовані а ос и ло ал но систе и координат. По на |
ченн кінцеви реакцій від ді |
кожно о одинично о кінцево о пере і енн наведені на рис. . . |
|
|
ис. . |
|
|
|
а авершенн |
навод т с |
еле енти атриц |
жорсткості стержн |
в ло ал ній систе |
і коор |
динат при рі ни |
ранични у |
ова , о одержані |
а допо о ою фор |
ули 6.33 . а е ці |
атриці |
станут в на оді при по удові |
атриці жорсткості всіє скінченно-еле |
ентно оделі плоско стер |
|||
жнево систе и. |
|
|
|
|
|
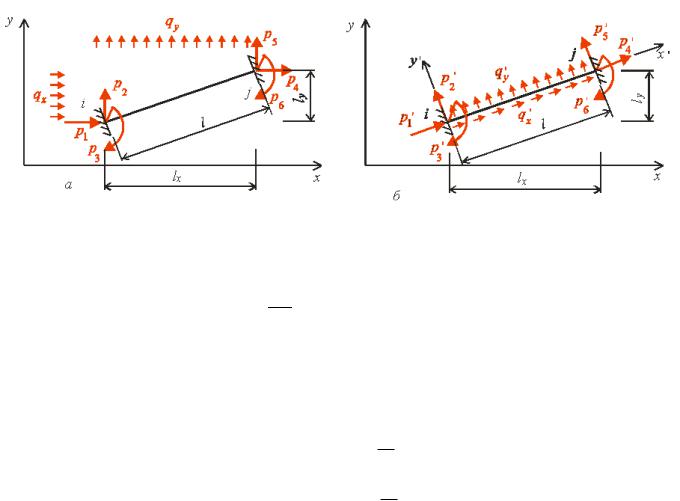
Е в ормі мето |
перемі ен |
23 |
а авершенн |
навод т с |
еле енти атриц |
жорсткості стержн |
в ло ал ній систе |
і коор |
динат при рі ни |
ранични у |
ова , о одержані |
а допо о ою фор |
ули 6.33 . а е ці |
атриці |
станут в на оді при по удові |
атриці жорсткості всіє скінченно-еле |
ентно оделі плоско стер |
|||
жнево систе и. |
|
|
|
|
|
6.6.1.орсткий вузол на початку і на кінці стержня рис.6.12
|
|
|
|
|
|
|
|
ис.6.12 |
k |
k |
|
k |
k |
|
fcos2 |
12i sin2 , |
|
11 |
|
44 |
14 |
|
41 |
|
l2 |
|
|
|
|
|
|
|
2 |
12i |
2 |
k22 |
k55 |
k25 |
k52 |
fsin |
l2 |
cos , |
||
k33 |
k66 |
4i , |
|
|
|
|
|
|
k |
|
k |
|
|
k |
|
|
k |
|
|
|
k |
|
|
k |
|
|
|
k |
|
|
|
k |
|
|
|
f |
12i |
sin cos , |
|
(6.37) |
12 |
|
21 |
|
45 |
|
54 |
15 |
|
51 |
|
24 |
|
42 |
|
l2 |
|
|
|
|||||||||||||
k |
|
k |
|
k |
|
k |
|
|
k |
|
|
k |
|
|
k |
|
|
k |
|
|
6i sin , |
|
|
|
|||||||
13 |
|
|
31 |
|
16 |
|
|
61 |
|
46 |
|
|
64 |
|
|
34 |
|
|
43 |
l |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
k |
|
k |
|
k |
|
k |
|
k |
|
k |
|
k |
|
k |
|
6i cos , |
|
|
|||||||||||||
|
35 |
|
|
53 |
|
|
56 |
|
|
|
65 |
|
|
23 |
|
|
|
32 |
|
|
|
26 |
|
|
|
62 |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
k36 k63 2i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
одатні напр |
и ді |
кінцеви |
|
реакцій, |
кі виражают с |
а фор ула и |
. |
, о ражено на |
||||||||||||||||||||||
рис. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вектори вантажни |
кінцеви |
реакцій, орієнтовани |
а ос |
и локал но |
і |
ло ал но систе |
|||||||||||||||||||||||||
координат рис. . |
, від ро поділени |
в довж стержн |
навантажен |
|
|
||||||||||||||||||||||||||
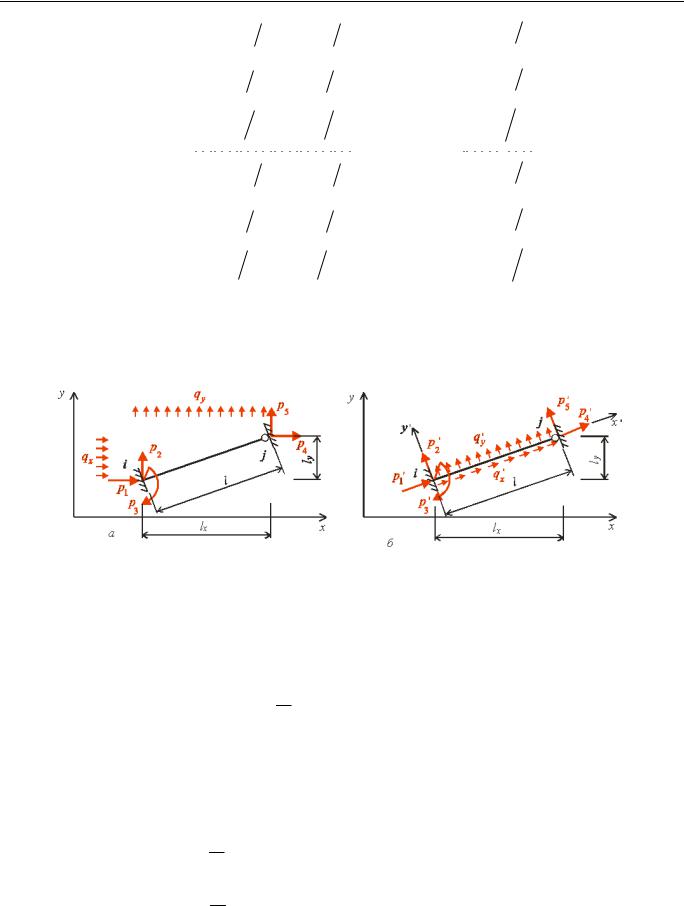
Е в ормі мето перемі ен 24
|
qxlyC 2 qylxS 2 |
|
qxly 2 |
|||
|
qxlyS 2 |
qylxC 2 |
|
qylx 2 |
||
|
qxly2 |
12 qylx2 12 |
|
qyl2 |
12 |
|
|
|
, |
|
. |
||
p |
|
|
p |
|
||
|
qxlyC 2 qylxS 2 |
|
qxly 2 |
|||
|
qxlyS 2 |
qylxC 2 |
|
qylx 2 |
||
|
qxly2 12 qylx2 12 |
|
qyl2 12 |
|||
ут і далі по начено S sin , |
|
C cos . |
|
|
|
|
6.6.2.орсткий вузол на початку і шарнірний вузол на кінці стержня рис.6.13
ис. .
оефіцієнти атриці жорсткості стержн
k |
k |
|
k |
k |
|
fcos2 |
3i sin2 , |
|
11 |
|
44 |
14 |
|
41 |
|
l2 |
|
|
|
|
|
|
|
2 |
3i |
2 |
k22 |
k55 |
k25 |
k52 |
fsin |
l2 |
cos , |
||
k33 |
3i, |
k66 |
|
0 , |
|
|
|
|
k |
|
k |
|
k |
|
|
|
k |
|
|
k |
|
k |
|
k |
|
k |
|
f |
3i |
sin cos , |
(6.38) |
12 |
|
21 |
|
45 |
|
|
54 |
|
15 |
|
51 |
|
24 |
|
42 |
|
l2 |
|
|
|||
k |
|
k |
31 |
|
k |
34 |
|
|
k |
43 |
3i sin , |
|
|
|
|
|
|
|
|
|||
13 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
k |
|
|
|
k |
|
3i cos , |
|
|
|
|
|
|
|
|
|||
|
35 |
|
53 |
|
|
|
23 |
|
|
|
32 |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k16 |
k26 |
|
k36 |
|
|
k46 |
k56 |
|
k66 |
|
k61 |
k62 |
k63 |
|
k64 k65 |
0 . |
||||||
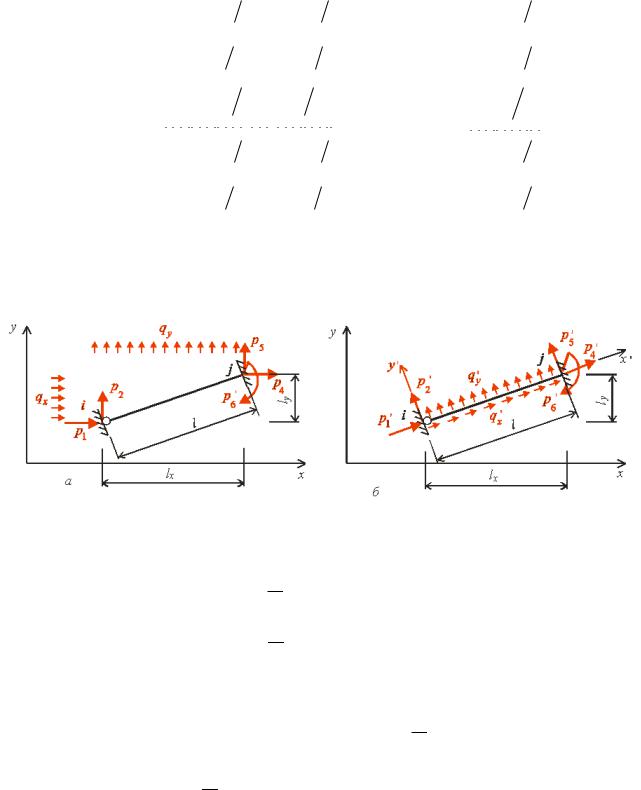
Е в ормі мето |
перемі ен |
25 |
Вектори вантажни |
реакцій, |
орієнтовани а ос |
и локал но |
і ло ал но систе координат, |
||
від ро поділени в довж стержн |
навантажен |
|
|
|||
|
5qxlyC 8 |
5qylxS 8 |
|
5qxly 8 |
||
|
5qxlyS 8 |
|
5qylxC 8 |
|
5qylx 8 |
|
|
qxly2 8 qylx2 8 |
|
qyl2 8 |
|||
p |
|
|
|
, |
p |
. |
|
3qxlyC 8 |
3qylxS 8 |
|
3qylx 8 |
||
|
3qxlyS 8 |
|
3qylxC 8 |
|
3qylx 8 |
|
|
|
|
0 |
|
|
0 |
6.6.3.арнірний вузол на початку і жорсткий вузол на кінці стержня рис.6.14
ис.6.14
оефіцієнти атриці жорсткості стержн
k |
k |
|
k |
k |
|
fcos2 |
3i sin2 , |
|
11 |
|
44 |
14 |
|
41 |
|
l2 |
|
|
|
|
|
|
|
2 |
3i |
2 |
k22 |
k55 |
k25 |
k52 |
fsin |
l2 |
cos , |
||
k33 |
0, |
k66 |
3i , |
|
|
|
||
k |
|
k |
|
|
k |
|
|
|
k |
|
|
k |
|
k |
|
= |
k |
|
k |
|
f |
3i |
sin cos , |
(6.39) |
12 |
|
21 |
|
45 |
|
|
|
54 |
|
15 |
|
51 |
|
|
24 |
|
42 |
|
l2 |
|
|
|||
k |
|
k |
61 |
|
k |
46 |
|
|
k |
64 |
3i sin , |
|
|
|
|
|
|
|
|
|||||
16 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
k |
|
|
|
k |
|
3i cos , |
|
|
|
|
|
|
|
|
|||||
|
56 |
|
|
65 |
|
|
|
26 |
|
|
|
62 |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
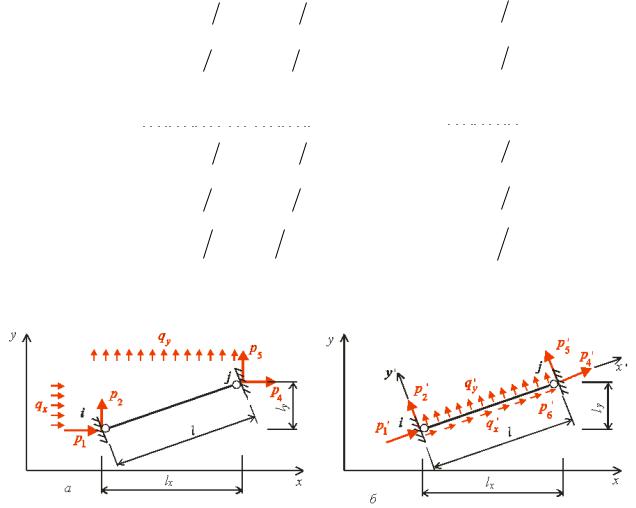
Е в ормі мето |
перемі ен |
26 |
k13 k23 k33 |
k43 |
k53 k63 |
k31 |
k32 k34 |
k35 k36 |
0 . |
|
Вектори кінцеви |
сил, |
орієнтовани |
а ос |
и локал но |
і ло ал но |
систе и координат, від |
|
ро поділени в довж стержн навантажен |
|
|
|
|
|
||
|
3qxlyC 8 3qylxS 8 |
|
|
3qxly 8 |
|||
|
3qxlyS 8 3qylxC 8 |
|
|
3qylx 8 |
|||
|
|
0 |
|
|
|
0 |
|
|
|
|
. |
|
. |
||
p |
|
|
|
p |
|
||
|
5qxlyC 8 5qylxS 8 |
|
|
5qxly 8 |
|||
|
5qxlyS 8 5qylxC 8 |
|
|
5qylx 8 |
|||
|
|
qxly2 8 qylx2 8 |
|
|
qyl2 8 |
||
6.6.4.арнірні вузли на початку і на кінці стержня рис.6.15
ис. .
оефіцієнти атриці жорсткості стержн дорівнюют .
k |
k |
44 |
k |
k |
41 |
fcos2 , |
|
|
|
|
|
|
|
11 |
|
14 |
|
|
|
|
|
|
|
|
|
||
k22 |
k55 |
k25 |
k52 |
fsin2 , |
|
|
|
|
|
|
|||
k12 |
k21 |
k45 |
k54 |
|
k15 |
k51 |
k24 |
k42 |
fsin cos , |
(6.40) |
|||
k16 |
k61 |
k46 |
k64 |
k56 |
k65 |
k26 |
k62 |
k33 |
k66 |
0 , |
|
||
k13 |
k23 |
k33 |
k43 |
k53 |
k63 |
k31 |
k32 |
k34 |
k35 |
k36 0 . |
|
||
Вектори кінцеви сил, орієнтовани |
а ос |
и локал но і |
ло ал но систе |
координат, від |
|||||||||
ро поділени |
в довж стержн навантажен |
|
|
|
|
|
|
||||||

6. МСЕ в формі методу переміщень |
27 |
Вектори кінцевих сил, орієнтованих за осями локальної і глобальної систем координат, від
розподілених вздовж стержня навантажень
|
− qxl yC 2 − q ylxS 2 |
|
|
′ |
2 |
||
|
|
− qxl y |
|||||
|
|
|
|
|
|
|
|
|
|
− q ylxC 2 |
|
|
|
|
|
|
qxl y S 2 |
|
|
− q′ylx |
2 |
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
p = |
|
, |
p′ = |
′ |
. |
||
|
|
|
|
|
|
|
|
|
− qxl yC 2 − q ylxS 2 |
|
− qxl y |
2 |
|||
|
|
|
|
|
|
|
|
|
qxl y S 2 |
− q ylxC 2 |
|
− q′ylx 2 |
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
||
6.7. Вузлові характеристики скінченно-елементної моделі
Вузли з скінченно-елементної з моделі з можуть з бути з охарактеризовані з як зі з статичного, з так з і з з кі-
нематичного боку. Кінематичними характеристиками є вузлові переміщення, а статичними − вуз-
лові реакції і вузлові навантаження.
Будь-який з вільний з жорсткий з вузол i з скінченно-елементної з моделі з має з три з ступня з вільності,
тобто можливість двох поступальних і одного кутового переміщень xi , yi , ϕi цього вузла
(див.рис.6.16,а).
Рис.6.16
Зазначені величини можуть бути записані у вигляді вектора
Ti = { xi |
yi |
ϕi}. |
Шарнірний вузол має два ступня вільності (рис.6.16,б) і відповідно вектор переміщень такого вузла матиме дві компоненти:
Ti = { xi |
yi}. |
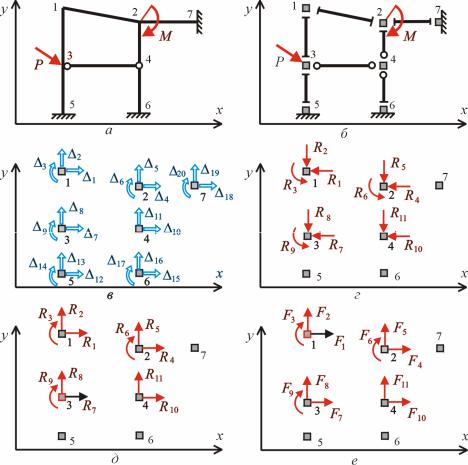
6. МСЕ в формі методу переміщень |
28 |
Розглянемо розрахункову схему рами (рис.6.17,а). Сукупність всіх вузлових переміщень скін-
ченноелементної моделі (рис.6.17,б) становить вектор вузлових переміщень
|
T = { 1 |
|
2 … |
i |
… |
7} , |
|
|
||||||
aбо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = { x1 |
y1 ϕ1 |
|
|
x2 |
y2 |
ϕ2 |
|
|
,…, |
|
x7 |
y7 |
ϕ7 }. |
|
|
|
|
||||||||||||
Для практичних розрахунків зручно використовувати наскрізну нумерацію компонентів вуз-
лових переміщень у межах усієї моделі (рис.6.17,в).
У такому разі вектор вузлових переміщень матиме вигляд:
T = { 1 |
2 |
3 |
|
5 |
6 |
|
,…, |
|
18 |
19 |
20}. |
4 |
|
|
Вектор при розрахунку стержневих систем за методом скінченних елементів у формі мето-
ду переміщень являє собою вектор основних невідомих. При цьому деякі переміщення вузлів мо-
жуть бути відомі з граничних умов задачі. Так, у даному прикладі
12 = 13 = 14 = …= 20 = 0.
Рис.6.17

6. МСЕ в формі методу переміщень |
29 |
Отже, невідомими є переміщення 1, 2 ,…, 11 . Вектор |
|
після вилучення нульових елеме- |
|
нтів набере вигляду |
|
T = { |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
} . |
|
11 |
Під з впливом зовнішніх з факторів з вузли з скінченно-елементної з моделі зпереміщуються, з а з стерж-
ні, які їх поєднують, деформуються. Поміж вузлами і стержнями виникають реакції взаємодії − одна із статичних характеристик вузлів. Сумарні реакції всіх стержнів, які примикають до вузла i,
зобразимо у вигляді двох зосереджених сил, які орієнтовані за осями глобальної системи коорди-
нат всієї моделі, і зосередженого моменту. Позначимо ці реакції через Відповідні реактивні сили, які передаються на вузли з боку стержнів, і на стержні, що приєд-
нуються до вузлів, однакові за величиною, але спрямовані в протилежних напрямах. Звичайно для реактивних сил, з якими вузли діють на стержні, за додатні приймають напрями, що збігаються з напрямами вузлових переміщень (рис.6.17,д). Отже, реакції, які передаються на вузли з боку стер-
жнів, будуть спрямовані протилежно (рис.6.17,г).
Сукзупність зреакцій здля зжорсткого звузла i з скінченно-елементної змоделі зподамо з у звигляді звекз-
тора:
|
= {Rxi Ryi |
Rϕi } , |
||
RTi |
||||
|
|
|
|
i |
а для шарнірного |
|
|
|
|
|
|
= {Rxi |
Ryi } . |
|
RTi |
||||
|
|
|
|
i |
Вузлові реакції скінченно-елементної моделі утворюють вектор вузлових реакцій:
RT = {R1 R2 … Rn} .
При розв’язанні практичних задач використовується наскрізна нумерація реакцій, причому їх номери повинні збігатися з номерами відповідних переміщень:
|
|
|
|
|
|
|
|
|
|
|
RT = {R R R R R R R R R R R } . |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Іншою з статичною з характеристикою з вузлів з скінченно-елементної з моделі з є з вузлові з навантажен-
ня. В кожному вузлі припускається можливість дії трьох компонентів зовнішніх зосереджених си-
лових дій: Fx − сила, яка спрямована вздовж осі x глобальної системи координат; Fy − сила, яка діє вздовж осі y; Fϕ − зосереджений момент. Зосереджені дії у жорсткому вузлі i можуть бути
записані у вигляді вектора
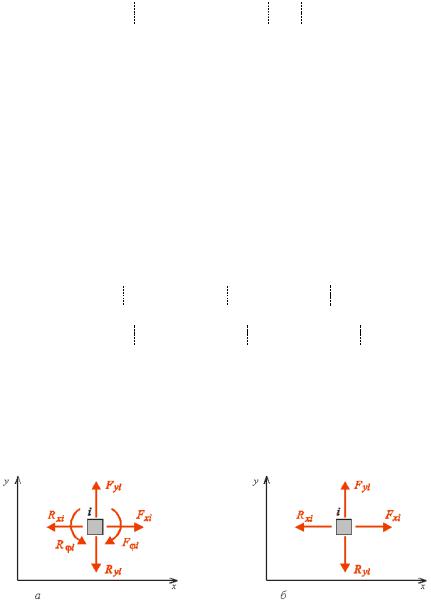
Е в ормі мето |
перемі ен |
30 |
|
|
|
|
|
|
|
FiT |
Fxi |
|
Fyi |
F i , |
|
|
|
|
|
а сукупніст |
ведени |
до ву лів скінченно-еле |
ентно |
оделі навантажен |
рис. . . |
у ви л ді |
||||||||||
вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FT |
|
F1 |
F2 |
|
Fn |
|
|
|
|
|
|
|
|
|
Fx1 Fy1 F 1 Fx2 Fy2 |
F 2 |
Fxn |
Fyn |
F n . |
|
|
||||||
Вектор |
F пода |
о |
к су у дво |
векторів |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
F |
P |
|
Q, |
|
|
|
(6.41) |
|
де P |
вектор овнішні |
сил, |
о е посередн о діют на ву ли, йо о ко поненти дорівнюют |
від |
||||||||||||
повідни |
овнішні |
силови |
ді |
Q |
вектор |
ведени |
до ву лів ро поділени у ежа |
стержнів |
||||||||
навантажен . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
о |
поненти |
адани векторів також одержуют наскрі ну ну |
ерацію, |
ка відповідає ну |
ера |
|||||||||||
ці ву лови |
пере |
і |
ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PT |
|
P1 P2 P3 P4 P5 P6 P7 |
P8 P9 P10 P11 , |
|
|
|||||||||
|
|
QT |
|
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 . |
|
|
||||||||||
6.8. Матриця жорсткості скінченно-елементної моделі |
|
|
|
|
||||||||||||
у |
ов рівнова и уд - ко о ву ла |
i, |
жорстко о рис. . ,а а о шарнірно о рис. . |
, |
ає |
|||||||||||
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ис. .
Fx |
0, |
Fxi |
Rxi |
0 , |
Fx |
0, |
Fxi |
Rxi |
0 , |
|
|
|
|
|
|||||
Fy |
0, |
Fyi |
Ryi |
0, |
Fy |
0, |
Fyi |
Ryi |
0. |
M |
0, |
F i |
R i |
0 . |
|
|
|
|
|
6. МСЕ в формі методу переміщень |
31 |
або в матричній формі:
|
|
|
|
Fi |
− Ri |
= 0 . |
(6.42) |
Отже, для всіх вузлів скінченно-елементної моделі можна записати |
|
||
|
|
|
|
F |
− R = 0 |
|
|
або |
|
|
|
|
|
|
(6.43) |
R − F = 0 . |
|||
Вузлові реакції, що зумовлені переміщеннями вузлів, для лінійно-деформованих систем мо-
жуть бути представлені виразами:
R1 |
= |
K1,1 |
1 |
+ |
K1,2 |
2 |
+ … + |
K1,n n , |
R2 = |
K2,1 |
1 |
+ |
K2,2 |
2 |
+ … + K2,n n , |
||
|
|
|
|
|
|
|
|
(6.44) |
|
|
|
|
|
|
|
|
|
Rn |
= Kn,1 1 |
+ Kn,2 2 |
+ … + Kn,n n . |
|||||
У матричній формі лінійне перетворення (6.44) може бути записане у вигляді:
|
|
|
|
|
(6.45) |
|
R = K , |
|
|
||
де K− матриця жорсткості всієї скінченно-елементної моделі: |
|
||||
K |
K |
|
K |
|
|
1,1 |
1,2 |
|
1,n |
|
|
|
K2,2 |
|
|
|
|
K2,1 |
… |
K2,n |
|
||
K = |
|
|
|
. |
(6.46) |
|
|
|
|
||
|
Kn,2 … |
|
|
|
|
|
|
|
|
||
Kn,1 |
Kn,n |
|
|||
Довільний коефіцієнт Ki, j являє собою вузлову реакцію Ri |
, що викликана вузловим перемі- |
||||
щенням j = 1, за умови, що всі інші переміщення вузлів дорівнюють нулю.
Головні коефіцієнти матриці жорсткості являють собою додатні числа ( Ki,i >0). Побічні кое-
фіцієнти симетричні відносно головної діагоналі, тобто Ki, j |
= K j,i . |
||
Підставивши (6.45) у рівняння рівноваги (6.43), одержимо: |
|||
|
|
|
(6.47) |
K |
− F = 0 . |
||
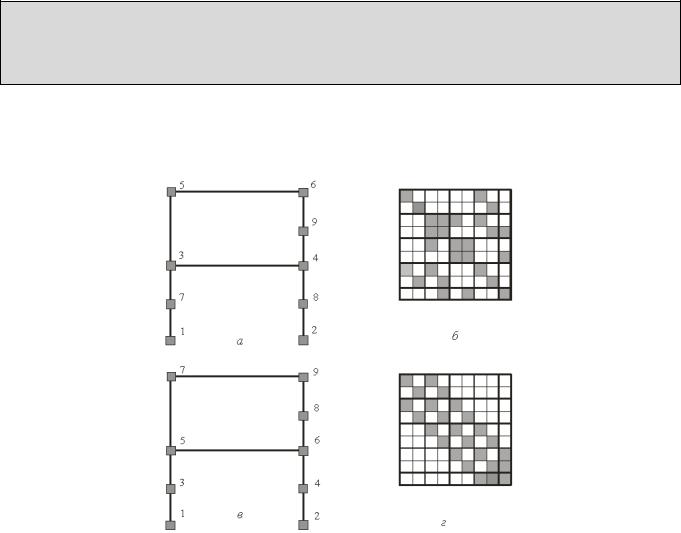
6. МСЕ в формі методу переміщень |
32 |
Такі самі рівняння в координатній формі представлятимуться співвідношеннями:
K1,1 |
1 |
+ |
K1,2 |
2 |
+ … + K1,n n |
− F1 |
= 0, |
K2,1 |
1 |
+ |
K2,2 |
2 |
+ … + K2,n n |
− F2 |
= 0, |
|
|
|
|
|
|
|
(6.48) |
|
|||||||
Kn,1 1 |
+ Kn,2 2 |
+ … + Kn,n n − Fn = 0. |
|||||
Невідомими в рівняннях (6.48) є переміщення вузлів, коефіцієнти − величини вузлових реак-
цій, вільні члени − вузлові навантаження.
Як вже зазначалось, будь-який коефіцієнт матриці жорсткості скінченно-елементної моделі
Ki, j являє собою вузлову реакцію Ri , що зумовлена вузловим переміщенням j = 1. На цій
підставі для обчислення коефіцієнтів матриці жорсткості необхідно почергово надавати одиничні переміщення звузлам зскінченно-елементної змоделі зі знаходити зсили, зякі зпередаватимуться зпри зцьо-
му на вузли. Величини цих сил визначаються елементами відповідних матриць жорсткості окре-
мих скінченних елементів.
Необхідно зважити на те, що вузлові реакції в дискретній моделі виникають лише у вузлі, що
переміщується, а також у вузлах, які пов’язані з ним стержнями. Тому загальний вигляд матриці
жорсткості скінченно-елементної моделі істотно залежить від того, як пронумеровано її вузлиз.
Розглянемо, наприклад, дискретну модель стержневої системи з двома різними системами ну-
мерації вузлів. Блочна схема матриці жорсткості, що відповідне першій системі нумерації
(рис.6.19,а), наведена на рис.6.19,б.
Рис.6.19
6. МСЕ в формі методу переміщень |
33 |
Клітинка схеми на перетині рядка n і стовпця m позначає блок вузлових реакцій у вузлі n від примусових переміщень вузла m. Зафарбовані клітинки характеризують наявність, а не зафарбова-
ні − відсутність реакцій. Так, від примусових переміщень вузла 4 реакції можуть виникнути у вуз-
лах 3, 4, 8 і 9. Тому відповідні клітинки зафарбовані в четвертому стовпці.
Іншій системі нумерації вузлів (рис.6.19,в) відповідає блочна схема матриці жорсткості, яку наведено на рис.6.19,г. У даному випадку ненульові блоки згруповано біля головної діагоналі,
тобто матриця має квазідіагональну структуру. Така матриця є більш придатною для розміщення в пам’яті комп’ютера і потребує менше часу для розв’язання системи рівнянь. Тому з двох систем нумерації вузлів перевагу слід віддати другій системі.
Взагалі під час нумерації вузлів слід ставити за мету, щоб найбільша різниця між номерами сусідніх вузлів була мінімальною. Скажімо, в першій системі нумерації (рис.6,19,а) найбільша різ-
ниця дорівнює шести, а в другій (рис.6.19,в) − лише двом.
Для з одержання з матриці з жорсткості з скінченно-елементної з моделі з можна застосувати з так звану структурну матрицю (матрицю інциденцій). З цією метою всі матриці жорсткості окремих скін-
ченних елементів поєднуються в одну квазідіагональну матрицю:
|
K1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
0 |
K 2 |
|
0 |
. |
K = |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
K m |
||
Дана матриця описує стан m скінченних елементів, які не пов’язані між собою. Оскільки ж скінченні елементи мають спільні вузли стиковки, їх необхідно поєднати в загальну систему. Зад-
ля цього може бути побудовано структурну матрицю I. Кожен стовпець матриці I повинен відпо-
відати з одному з узагальненому з переміщенню з скінченно-елементної з моделі, з кожен з рядок − з одному кінцевому з переміщенню з скінченного з елемента. з При з цьому, з якщо з переміщення з кінця з стержня з від-
повідає з переміщенню з вузла з скінченно-елементної з схеми, з елемент з структурної з матриці з беруть за одиницю, в іншому разі − за нуль.
Наприклад, з розглянемо з побудову з структзурної з матриці з для з скінченно-елементної з моделі, з що зображена на рис.6.20,а. Вектор вузлових переміщень матиме 6 компонентів:
T = { 1 |
2 |
3 |
4 |
5 |
6} . |
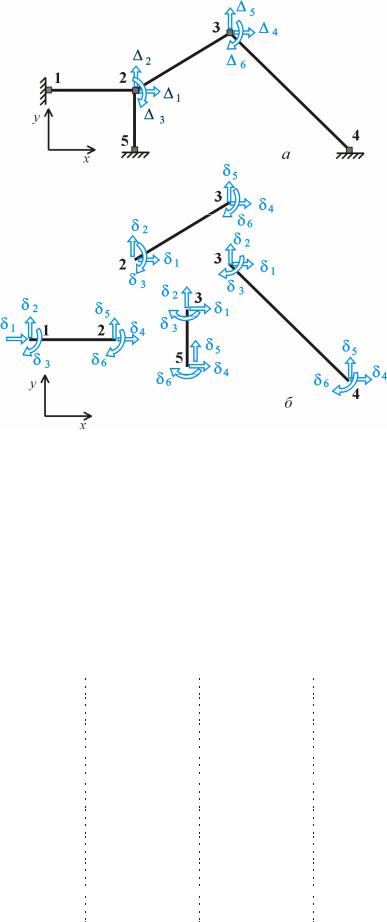
6. МСЕ в формі методу переміщень |
34 |
Рис.6.20
На з рис.6.20.б зображено з для з всіх з стержнів з скінченно-елементної з моделі з кінцеві з переміщення,
які орієнтовані за осями глобальної системи координат. Треба звернути увагу на те, що кінцеві пе-
реміщення стержнів нумеруються залежно від того, чи належить вузол до початку або до кінця стержня. Так, горизонтальне переміщення 4 з вузла 3 з скінченно-елементної з моделі з на з стержні 2-3
позначене як δ4, а на стержні 3-4 − як δ1.
Отже, маємо структурну матрицю
0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 T
|
|
|
|
0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 |
|
|
|
0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 |
|
I = |
. |
|
|
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 |
|
|
|
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 |
|
|
|
|
|
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 |
|
|
|
6. МСЕ в формі методу переміщень |
35 |
Матриця жорсткості скінченно-елементної моделі може бути отримана з добуткзу:
T ~ |
(6.49) |
K = I K I. |
При цьому матриця жорсткості виявляється виродженою, оскільки всі скінченні елементи пе-
редбачалися не закріпленими від переміщень. Для виправлення матриці з неї треба вилучити всі
нульові рядки.
Зміст табл. 6.3. характеризує взаємну стиковку елементів, тобто матрицю інциденцій I.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 6.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
Скінченний |
1 |
2 |
3 |
4 |
5 |
6 |
елемент |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
δ1 |
|
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ2 |
|
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ3 |
1-2 |
||||||
1 |
0 |
0 |
0 |
0 |
0 |
δ4 |
|
||||||
0 |
1 |
0 |
0 |
0 |
0 |
δ5 |
|
||||||
0 |
0 |
1 |
0 |
0 |
0 |
δ6 |
|
||||||
1 |
0 |
0 |
0 |
0 |
0 |
δ1 |
|
||||||
0 |
1 |
0 |
0 |
0 |
0 |
δ2 |
|
||||||
0 |
0 |
1 |
0 |
0 |
0 |
δ3 |
2-3 |
||||||
0 |
0 |
0 |
1 |
0 |
0 |
δ4 |
|
||||||
0 |
0 |
0 |
0 |
1 |
0 |
δ5 |
|
||||||
0 |
0 |
0 |
0 |
0 |
1 |
δ6 |
|
||||||
1 |
0 |
0 |
0 |
0 |
0 |
δ1 |
|
||||||
0 |
1 |
0 |
0 |
0 |
0 |
δ2 |
|
||||||
0 |
0 |
1 |
0 |
0 |
0 |
δ3 |
2-5 |
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ4 |
|
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ5 |
|
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ6 |
|
||||||
0 |
0 |
0 |
1 |
0 |
0 |
δ1 |
|
||||||
0 |
0 |
0 |
0 |
1 |
0 |
δ2 |
|
||||||
0 |
0 |
0 |
0 |
0 |
1 |
δ3 |
3-4 |
||||||
0 |
0 |
0 |
0 |
0 |
0 |
δ4 |
|
||||||
0 |
0 |
0 |
|
0 |
|
0 |
|
0 |
δ5 |
|
|||
0 |
0 |
0 |
|
0 |
|
0 |
|
0 |
δ6 |
|
|||
6.9. Визначення зусиль у стержнях
Із рівнянь рівноваги (6.47) визначається вектор вузлових переміщень
|
= K |
|
(6.50) |
|
−1F |
і таким чином стають відомими переміщення всіх вузлів. Внаслідок нерозривності деформацій скінченно-елементної з моделі з кінці з стержнів, з що з примикають з до з вузлів, з які з переміщзуються, з мати-

Е в ормі мето |
перемі ен |
36 |
ут такі са і пере і |
енн . Отже, дл |
кожно о стержн |
e скінченно-еле |
ентно |
оделі |
ожна по |
|||||||||
удувати вектор кінцеви пере і |
ен |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
xi |
|
|
|
|
|
|
|
|
|
|
|
δe |
|
2 |
yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
δi |
|
3 |
i |
. |
|
|
|
|
(6.51) |
|
|
|
|
|
|
|
δj |
|
4 |
xj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
yj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
j |
|
|
|
|
|
|
у |
арні кінцеві реакці |
стержн |
рис. . |
,а |
складают с |
кінцеви |
реакцій ri |
, |
кі |
у овле- |
|||||
ні пере |
і енн |
и ву лів скінченно-еле ентно |
оделі |
. |
і кінцеви и сила и |
pi |
, |
о спричи |
|||||||
нені дією ро поділено о на стержні овнішн о о навантаженн |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
se |
re pe , |
|
|
|
|
|
|
(6.52) |
|
де se |
вектор су |
арни |
кінцеви |
реакцій еле |
ента e: |
|
|
|
|
|
|
|
|||
|
|
|
s T |
si |
sj |
s1 |
|
s2 s3 |
s4 |
s5 s6 . |
|
|
|
|
|
|
|
ис. . |
|
|
і су арни кінцеви реакцій у |
овлює внутрішні усилл на кінц |
стержн рис. . , . |
||
Очевидно, о |
|
|
|
|
s1 |
Ni , s4 |
N j , |
|
|
s2 |
Qi , |
s5 |
Qj , |
(6.53) |
s3 |
Mi , |
s6 |
M j . |
|
аки чино , вектор су арни кінцеви реакцій пов' аний внутрішні и усилл и

Е в ормі мето |
перемі ен |
37 |
|
|
|
seT |
|
|
|
Ni |
|
Qi |
Mi |
|
N j |
|
|
|
Qj |
|
|
|
M j |
e . |
|
(6.54) |
||||||||||||||||||
іншо о |
оку, вектор кінцеви |
реакцій виражаєт с чере |
|
|
вектор кінцеви |
пере і ен |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
re |
keδe |
keTeδe . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.55) |
||||||||||||||
оді |
. |
ає |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
se |
ke |
|
eδe |
|
|
|
e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.56) |
|||||||
По начивши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
he |
keTe , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.57) |
|||||||||
наса кінец |
|
оже о |
аписати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
se heδe |
pe. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.58) |
|||||||||
Ви л д |
|
атриці he алежит |
|
від ранични |
|
у |
ов на кінц |
|
|
|
стержн . ак, дл стержн , |
о ає |
|||||||||||||||||||||||||||||
на о о кінц |
|
жорсткі ву ли, післ |
пере |
ноженн |
|
атриц |
ідно |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
fC |
|
|
|
fS |
|
0 |
|
|
|
|
|
fC |
|
|
|
|
fS |
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
12i |
S |
|
12i |
C |
|
6i |
|
|
12i |
|
S |
|
|
|
12i |
C |
|
|
6i |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|||||||||||||||||
|
|
|
|
|
|
l2 |
|
l2 |
|
|
|
|
l2 |
|
|
|
|
l2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
6i |
|
S |
|
|
|
6i |
|
C |
4i |
|
|
|
|
6i |
|
S |
|
|
6i |
|
C |
|
2i |
. |
(6.59) |
|||||||||||
|
|
|
he |
|
l |
|
|
|
l |
|
|
|
|
l |
|
|
|
l |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||
|
|
|
|
fC |
|
|
|
fS |
|
|
|
|
|
fC |
|
|
|
|
fS |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
12i |
S |
|
12i |
C |
6i |
|
|
12i |
S |
12i |
C |
|
6i |
|
|
|||||||||||||||||||||||
|
|
|
|
|
l2 |
|
|
|
l2 |
l |
|
|
|
|
|
l2 |
|
|
l2 |
|
l |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
6i |
|
S |
|
|
|
6i |
|
C |
2i |
|
|
|
|
6i |
|
S |
|
|
6i |
|
C |
|
4i |
|
|
|||||||||||
|
|
|
|
|
|
l |
|
|
|
l |
|
|
|
|
l |
|
|
|
l |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
||||||||||
ут, к і раніше, по начено S |
|
|
|
sin , |
C |
cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
6.10. озрахунок плоскої шарнірно-стержневої системи методом скінченних елементів
ео ідно о числити |
усилл в стержн |
шарнірно-стержнево систе и рис. . ,а , о ава |
||
нтажена ву лови и сила |
и P1 40 |
і P2 |
60 |
. |
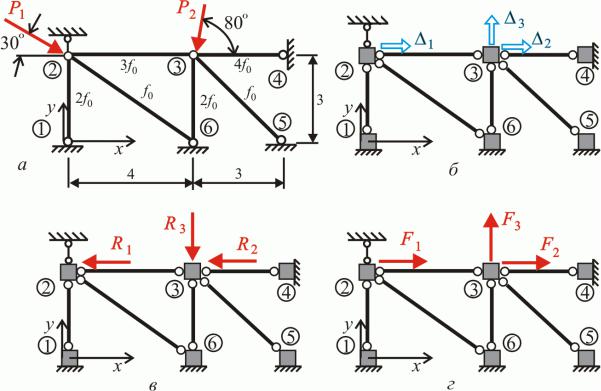
Е в ормі мето |
перемі ен |
38 |
|
|
ис. . |
6.10.1. Геометричні характеристики стержнево системи |
||
Початок |
ло ал но систе и координат прийн то у ву лі . оординати ву лів ви начає о а |
|
с е ою. |
ео |
етричні арактеристики стержнів о числює о а фор ула и (6.1) – (6.2). е ул тати |
о числен |
аноси о у та л. . . |
|
П.-к.* |
x |
y |
п |
x |
y |
xк |
xп |
yк yп |
l |
sin |
cos |
f |
|
п |
|
к |
к |
|
|
|
|
|
|
|
|
2-3 |
0 |
3 |
4 |
3 |
4 |
|
0 |
4 |
0 |
1 |
3 f0 |
|
3-4 |
4 |
3 |
7 |
3 |
3 |
|
0 |
3 |
0 |
1 |
4 f0 |
|
1-2 |
0 |
0 |
0 |
3 |
0 |
|
3 |
3 |
1 |
0 |
2 f0 |
|
3-6 |
4 |
3 |
4 |
0 |
0 |
|
-3 |
3 |
-1 |
0 |
2 f0 |
|
2-6 |
0 |
3 |
4 |
0 |
4 |
|
-3 |
5 |
-0.6 |
0.8 |
f0 |
|
3-5 |
4 |
3 |
7 |
0 |
3 |
|
-3 |
4.243 |
-0.707 |
0.707 |
f0 |
|
П.-к. – тут і далі но ери початку і кінц |
скінченно о еле |
ента |
|
|
|
||||
6.10.2. узлові характеристики скінченно-елементно моделі |
|
|
|||||||
твори о дискретну одел |
конструкці .. |
|
а ву ли о ере |
о точки перетину стержнів. |
ожен |
||||
віл ний ву ол |
оделі є шарнірни |
і то |
у ає два ступн |
віл ності. |
ожливі напр и пере і |
ен і |
|||
ну ерацію |
о ражено на рис. . |
, . |
апише |
о ву лові пере |
і енн |
у ви л ді вектора |
|
||
|
|
|
T |
2 |
2 |
3 . |
|
|
|
|
|
|
|
|
|
|
|||
Е в ормі мето |
перемі ен |
39 |
|
ву лі |
ро ташовано вертикал ний опорний стержен , |
і то у вертикал но о ву лово о пере |
|||||||||||||
і |
енн ву ла не |
уде. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а рис. |
. ,в |
о ражено ву лові реакці , |
кі передают с |
на стержні систе |
и |
оку |
ву лів. |
||||||||
|
ну ераці |
відповідає ну ераці ву лови |
пере |
і |
ен . |
еакці , |
о відповідає нул ово |
у пере |
||||||||
і |
енню, до ува и не ерет с . апише |
о вектор ву лови |
реакцій |
|
|
|
|
|||||||||
|
|
|
|
|
|
RT |
R1 |
R2 |
R3 . |
|
|
|
|
|
||
|
Вектор ву лови |
навантажен , |
о ражени на рис. . |
, , |
апише о анало ічно |
|
|
|||||||||
|
|
|
|
|
|
FT |
F1 |
F2 |
F3 . |
|
|
|
|
|
||
|
При о численні еле |
ентів дано о вектора вра ує |
о, |
о вектор сил, кі передают с на ву ли |
||||||||||||
оку стержнів від про онови навантажен , є нул ови , оскіл ки |
овнішнє навантаженн |
на стер |
||||||||||||||
жні відсутнє, і то |
у F |
P . Еле енти вектора P і, отже, вектора F є проекці |
и |
овнішні ву |
||||||||||||
лови навантажен |
|
на координатні осі |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
F1 |
P1 cos 30 |
34,64 |
|
, |
|
|
|
|
|||
|
|
|
|
|
F2 |
|
P2 cos 80 |
|
10,42 |
, |
|
|
|
|
||
|
|
|
|
|
F3 |
|
P2 sin 80 |
|
59,09 . |
|
|
|
|
|||
|
Вектор ву лови |
навантажен , таки |
чино , |
ає ви л д |
|
|
|
|
|
|||||||
|
|
|
|
|
FT |
34,64 |
10,42 |
59,09 . |
|
|
|
|||||
6.10.3. Розв язувальне рівняння методу скінченних елементів |
|
|
|
|
||||||||||||
|
апише |
о ро в |
увал не рівн нн |
|
|
|
|
|
|
|
|
|
|
|||
K F 0,
де K атриц жорсткості всіє систе и
|
K |
K1,1 |
K1,2 |
K1,3 |
|
|
K2,1 |
K2,2 |
K2,3 . |
|
|
|
|
K3,1 |
K3,2 |
K3,3 |
|
атричне рівн нн рівнова и ву лів |
ати е ви л д |
|
|||
K1,1 |
K1,2 |
K1,3 |
1 |
F1 |
0 |
K2,1 |
K2,2 |
K2,3 |
2 |
F2 |
0 . |
K3,1 |
K3,2 |
K3,3 |
3 |
F3 |
0 |
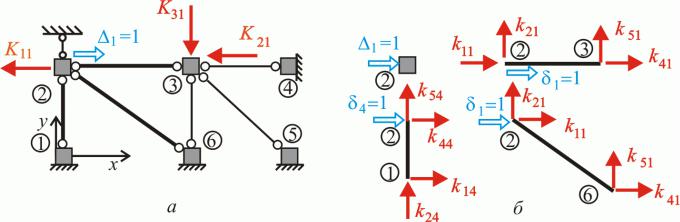
Е в ормі мето |
перемі ен |
40 |
6.10.4.Обчислення елементів матриці жорсткості
лви наченн еле ентів атриці жорсткості почер ово надавати е о віл ни ву ла скін
ченно-еле |
ентно |
оделі |
ожливі одиничні пере |
і |
енн . При ц о у стержні, |
кі при икают |
до |
||||||||||||||
ву ла, |
о пере і |
уєт с , дефор |
уют с . |
іж ву ла и і стержн |
и виникают реакці в ає оді . |
||||||||||||||||
ни |
складают с |
ву лові реакці , |
кі |
вл ют |
со ою еле енти |
атриці жорсткості всіє |
систе |
и. |
|||||||||||||
ауважи |
о, |
о всі стержні належат |
до четверто о типу, то то |
ают шарніри на о о |
кінц . |
|
|||||||||||||||
|
л |
ви наченн еле |
ентів першо о стовпц |
атриці жорсткості нада о дискретній |
оделі ву |
||||||||||||||||
лове пере |
і |
енн |
1 |
1 |
рис. . |
,а , вважаючи, |
о всі інші ву лові пере і |
енн |
дорівнюют |
||||||||||||
нулю. При |
|
аданій ді дефор уют с |
|
лише ті стержні, кі при |
икают |
до ву ла |
. Вони по начені |
||||||||||||||
на рис. . |
,а товсти |
и ліні |
и. |
ут також |
о ражено ву лові реакці |
Ki, j . Перший індекс |
це |
||||||||||||||
но |
ер реакці , дру ий |
но |
ер пере |
і |
енн , |
о |
у |
овило дану реакцію. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ис. . |
|
|
|
|
|
а рис. . |
, |
о ражено тіл ки ті стержні, о дефор |
уют с , а також кінцеві реакці |
в стерж |
|||||||
н , |
орієнтовані |
а ос |
и ло ал но |
систе и координат. Величини реакці ви начают с |
коефіці |
||||||||
єнта |
и атриці жорсткості (6.40) в |
ло ал ній систе |
і координат дл стержн четверто о типу. |
||||||||||
іставленн |
рисунків |
. |
,а і . |
, |
випливає |
|
|
|
|||||
K |
|
k 2 |
3 |
k 2 |
6 |
k1 |
2 |
|
|
|
|
|
|
1,1 |
11 |
|
11 |
44 |
|
|
|
|
|
|
|||
|
|
fcos2 2 3 |
fcos2 2 |
6 |
fcos2 1 2 |
0 |
0,64 f0 3 f0 3,64 f0, |
|
|||||
K2,1 |
k412 |
3 |
|
f cos2 2 3 |
|
3 f0, |
|
|
|
||||
K |
3,1 |
k2 |
3 |
|
f sin cos 2 |
3 |
|
0. |
|
|
|
||
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
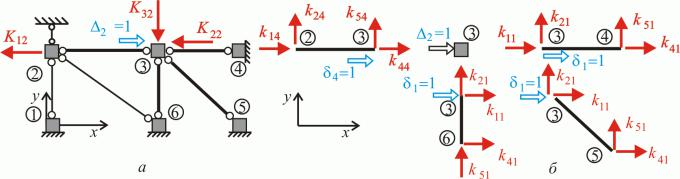
Е в ормі мето |
перемі ен |
41 |
|
|
ада |
о дискретній |
оделі |
рис. . |
,а |
ву лове пере |
і |
енн 2 |
1. Порівнюючи рис. . ,а і |
||||||
рис. . |
, |
оже о |
аписати |
|
|
|
|
|
|
|
|
|
||||
K |
|
k2 |
3 |
fcos2 2 3 |
|
3 f |
0 |
, |
|
|
|
|
|
|||
1,2 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
K |
2,2 |
k3 4 |
k3 5 |
k |
3 6 |
k |
2 3 |
|
|
|
|
|
|
|
||
|
11 |
11 |
11 |
|
44 |
|
|
|
|
|
|
|
||||
|
|
f cos2 3 |
4 |
|
f cos2 3 |
5 |
f cos2 3 6 |
f cos2 2 |
3 |
|||||||
|
|
4 f0 |
0,5 f0 |
0 |
3 f0 |
|
7,5 f0 , |
|
|
|
|
|||||
K |
3,2 |
k3 |
4 |
k3 |
5 |
k3 |
6 |
k2 |
3 |
|
|
f sin cos 3 4 |
|
|
|
|
|
21 |
21 |
|
21 |
54 |
|
|
|
|
|
|
|
||||
|
f sin cos 3 |
5 |
f sin cos 3 |
6 |
f sin cos 2 |
3 |
|
|||||||||
|
|
0 |
|
0,5 f0 |
0 |
0 |
|
0,5 f0. |
|
|
|
|
||||
|
|
|
ис. . |
|
Анало ічно |
на оди о ву лові реакці від пере і енн 3 1: |
|||
|
|
K1,3 |
0, |
|
|
|
K2,3 |
0,5 f0 , |
|
|
|
K3,3 |
2,5 f0 . |
|
рештою, |
атриц жорсткості всіє систе |
и ає такий ви л д |
||
|
|
3,64 f0 |
3 f0 |
0 |
|
K |
3 f0 |
7,5 f0 |
0,5 f0 . |
|
|
0 |
0,5 f0 |
2,5 f0 |
Е в |
ормі мето |
перемі ен |
|
|
|
|
42 |
||
6.10.5. изначення вузлових переміщень |
|
|
|
|
|
||||
о в |
ок атрично о рівн нн (6.47) ожна подати в фор |
і |
|
|
|||||
|
|
|
|
|
K 1F , |
|
|
|
|
де K 1 |
атриц , о ернена до атриці жорсткості всіє |
систе |
и K. |
|
|
||||
Отже, о числює о вектор ву лови пере |
і ен |
|
|
|
|
||||
|
1 |
1 |
0,41258 0,16728 |
0,03345 |
34,64 |
1 |
10,5721 |
||
|
|
|
|
|
|
|
|||
|
2 |
0,16728 0,20294 0,04059 |
10,42 |
1,2808 . |
|||||
|
f0 |
|
|
|
|
|
f0 |
|
|
|
3 |
0,03345 0,04059 0,40812 |
59,09 |
23,380 |
|||||
|
|
|
|
|
|
|
|
|
|
6.10.6. Обчислення зусиль у стержнях
л о численн усил
seT |
Ni Qi |
Mi |
N j |
Qj M j e |
використає о фор улу . |
|
|
|
|
|
se |
heδe |
pe , |
|
де вектор pe є нул ови , а атриц |
he ви начаєт с і |
співвідношенн (6.57) |
||
he keTe
і дл стержн четверто о типу становит
|
|
|
fC |
fS |
|
|
0 |
|
fC |
|
fS |
0 |
|
||
|
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
0 |
|
|
|
|
he |
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
0 . |
||
|
|
fC |
|
fS |
|
|
0 |
|
fC |
|
fS |
0 |
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
0 |
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
0 |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Еле |
енти вектора T |
|
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
кінцеви пере і ен скінченно о еле |
||
|
e |
1 |
|
|
|
|
|
|
|
|
|||||
ента в |
ло ал ній систе |
і координат ви начают с |
ко |
|
понента |
|
и вектора ву лови пере і ен |
||||||||
усіє систе и. ак, дл еле |
ента 2-3 |
|
ожна |
аписати |
|
|
|
|
|
||||||
|
|
T2 |
3 |
|
1 |
|
|
|
|
|
3 |
4 |
|
, |
|
дл еле ента -4 :

6. МСЕ в формі методу переміщень |
43 |
δT3−4 = {D3 D4 0 |
0 |
0 |
0 } , |
а для елемента 1-2 : |
|
|
|
δ1T−2 = { 0 0 0 D1 |
0 0 } . |
||
Обчислимо, наприклад, кінцеві зусилля в стержні 2-3. Матриця h2−3 для цього стержня ма-
тиме вигляд
|
|
|
|
|
3 |
0 |
0 |
− 3 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
h2−3 |
= f0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
|
× |
|
|
|
|
|
|
, |
||
|
|
|
|
- 3 |
0 |
0 |
3 |
0 |
0 |
||
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
||
вектор кінцевих переміщень |
|
|
|
|
|
|
|
|
|
||
δT2−3 = {10,5721 |
f0 |
0 |
0 |
|
1, 2808 |
f0 |
-23,380 f0 0} , |
||||
|
|||||||||||
а вектор q¢2T−3 = {0 0 0 |
|
0 0 |
0} . Виконавши згідно формули (6.58) матричні операції оде- |
||||||||
|
|||||||||||
|
|||||||||||
ржимо: |
|
|
|
|
|
|
|
|
|
||
s¢2T−3 = {27,8779 |
0 |
0 |
-27,8779 |
0 0} , |
|||||||
тобто в стержні 2-3 згинальні моменти і поперечні сили дорівнюють нулю, а поздовжня сила ста-
новить N2 −3 = −27,8779 кН.
Рис.6.25

Е в ормі мето |
перемі ен |
44 |
6.11.Приклад розрахунку рами за методом скінченних елементів
о ра ує о ра у |
рис. . |
при таки ви ідни |
дани |
l=4 |
h=3 |
1=1,8 |
2=1,2 |
||||
q1=2,4 |
|
2=2 |
к видно рисунку, ра а |
ає два типи скінченни |
еле ентів стержен і |
||||||
атисненн |
и |
о о |
сторін |
перший тип, стержен |
і |
атисненн |
на початку і шарніро |
на кінці |
|||
дру ий тип. |
|
|
|
|
|
|
|
|
|
|
|
ідно |
у |
овою |
одо жорсткостей еле |
ентів ра |
и |
уде |
о вважати, |
о дл вертикал ни сте |
|||
ржнів -2, |
1-6, 2-5, |
2-7, 3- |
жорсткості на |
ин становл т |
EI= , |
а на по довжні дефор аці |
|||||
EA= . |
л |
на илено о та |
ори онтал ни |
стержнів |
-5, 1-2, 2-3 відповідно EI=2 i EA=200. |
||||||
Початок ло ал но систе и координат прин то у ву лі .
6.11.1. Геометричні характеристики скінченних елементів
ео етричні арактеристики стержнів наведені в та л. . .
|
|
|
П. |
к. |
|
|
ип |
l |
|
|
sin |
|
cos |
|
|
EI |
|
|
EA |
|
|
i |
f |
|
|
||
|
|
|
|
|
|
|
Е |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
4 |
|
|
0 |
|
|
1 |
|
|
2 |
|
|
200 |
|
|
0,50 |
50,000 |
|
|
|
|
|
2 |
3 |
|
|
1 |
|
8 |
|
|
0 |
|
|
1 |
|
|
2 |
|
|
200 |
|
|
0,25 |
25,000 |
|
|
|
|
|
4 |
5 |
|
|
1 |
|
5 |
|
|
0,6 |
|
0,8 |
|
|
2 |
|
|
200 |
|
|
0,40 |
40,000 |
|
|
|
|
|
|
3 |
5 |
|
|
1 |
|
10 |
|
|
0,6 |
|
-0,8 |
|
|
2 |
|
|
200 |
|
|
0,20 |
20,000 |
|
|
|
|
|
|
1 |
6 |
|
|
2 |
|
3 |
|
|
-1 |
|
0 |
|
|
1 |
|
|
100 |
|
0,3333 |
33,333 |
|
|
||
|
|
|
2 |
7 |
|
|
2 |
|
3 |
|
|
-1 |
|
0 |
|
|
1 |
|
|
100 |
|
0,3333 |
33,333 |
|
|
||
|
|
|
3 |
8 |
|
|
2 |
|
3 |
|
|
-1 |
|
0 |
|
|
1 |
|
|
100 |
|
0,3333 |
33,333 |
|
|
||
|
|
|
1 |
4 |
|
|
1 |
|
3 |
|
|
1 |
|
|
0 |
|
|
1 |
|
|
100 |
|
0,3333 |
33,333 |
|
|
|
|
|
|
2 |
5 |
|
|
1 |
|
6 |
|
|
1 |
|
|
0 |
|
|
1 |
|
|
100 |
|
0,3333 |
16,667 |
|
|
|
6.11.2. Побудова векторів вузлових характеристик |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
искретну |
одел |
ра |
и |
ну ерацією напр ів |
|
ожливи |
пере і |
ен |
о ражено на рис. . . |
|||||||||||||||||
верніт ува у на те, |
о ну |
ераці |
напр |
ів пов |
ана |
ну |
ерацією ву лів |
спершу ну |
еруют с |
||||||||||||||||||
напр |
и у ву лі 1, поті у ву лі 2 то |
о. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Оскіл ки пере |
і |
енн |
опорни |
ву лів дорівнюют |
нулю, вектор невідо и ву лови |
пере і |
|||||||||||||||||||||
ен |
ати |
е ви л д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
T |
|
|
1 |
|
2 |
3 |
|
4 |
|
5 |
|
|
6 |
13 |
14 |
15 . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Отже, кіл кіст |
ступнів віл ності |
основни |
невідо |
и |
дорівнює п |
тнадц ти. |
|
||||||||||||||||||||
|
ак са |
о ожна аписати вектори ву лови |
реакцій і ву лови |
навантажен : |
|
||||||||||||||||||||||
|
|
|
RT |
|
|
R1 |
|
R2 |
R3 |
R4 |
R5 |
|
R6 |
R13 R14 R15 , |
|
||||||||||||

6. МСЕ в формі методу переміщень |
45 |
|
|
|
|
|
|
|
|
|
}. |
FT = { F F F F F F … F F F |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
13 |
14 |
15 |
|
|
Рис.6.26 |
|
|
Вектор вузлових навантажень F являє собою суму вектора P вузлових сил, які безпосередньо
діють на вузли дискретноі моделі, і вектора Q , який зумовлено дією на вузли розподілених на сте-
ржнях навантажень. Компоненти вектора F представлено на рис.6.27.
Рис.6.27
Вектор P може бути записано із порівняння діючих вузлових сил і моментів і схеми напрямів вільних переміщень вузлів. Зрештою, маємо:
|
= {0 0 0 0 0 0 1,8 0 0 1, 2 0 0 0 0 0} . |
PT |
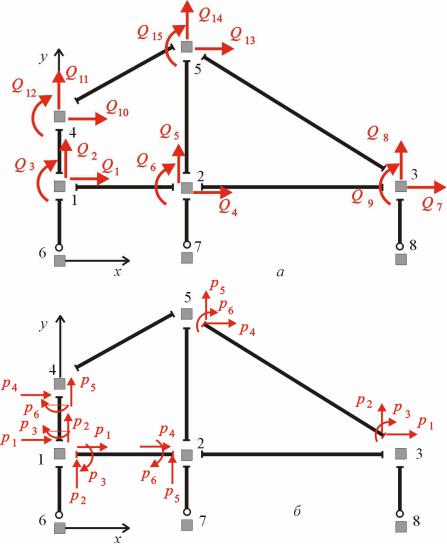
6. МСЕ в формі методу переміщень |
46 |
Компоненти з вектора Q з і з схема з кінцевих з сил, з що з передаються з на з вузли з скінченно-елементної моделі з боку завантажених стержнів, показано відповідно на рис.6.28,а та 6.28,б.
Рис.6.28
Для визначення компонентів вектора Q обчислимо кінцеві сили, що орієнтовані за осями гло-
бальної системи координат, в стержнях, на яких розташоване розподілене навантаження.
Стержень 1-2 (рис.6.29,а) має такі вихідні дані:
qx = 0, qy = −q1 = −2,4 кН м, lx = 4м, ly = 0.
м, lx = 4м, ly = 0.
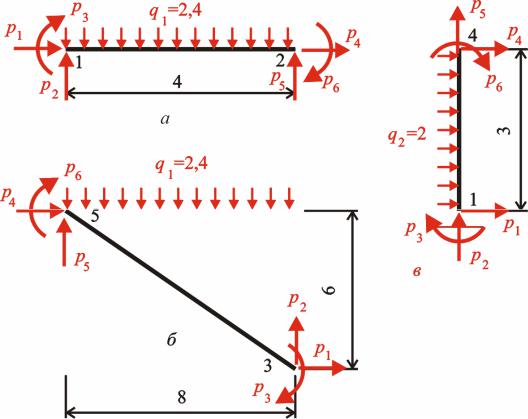
6. МСЕ в формі методу переміщень |
47 |
|
|
|
|
|
|
|
|
|
|
|
Рис.6.29 |
|
Отже, маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
p1 = 0, |
|
|
|
|
p4 = 0, |
|||||||
p |
2 |
= - |
(-2.4) × 4 |
|
= 4,8 кН, |
p = 4,8 кН, |
||||||
|
|
|
||||||||||
|
|
2 |
|
|
|
|
5 |
|||||
|
|
|
|
2 |
|
|
|
|
||||
p3 |
= |
(-2.4) × 4 |
|
= -3,2 кНм, |
p6 = 3,2 кНм. |
|||||||
12 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
Стержень 3-5 (рис.6.29,б) має такі дані: |
|
|||||||||||
q x = 0, |
|
|
q y = −q1 = −2.4 кН / м, |
lx = 8 м, l y = 6 м. |
||||||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
p1 = 0, |
|
|
|
|
p4 = 0, |
|||||||
p |
2 |
= - |
(-2.4) × 8 |
= 9,6 кН, |
p = 9,6 кН, |
|||||||
|
||||||||||||
|
|
|
2 |
|
|
|
|
5 |
||||
p3 |
= |
|
(-2.4) × 82 |
|
=12,8 кНм, |
p6 = -12,8 кНм. |
||||||
12 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
І нарешті, для стержня 1-4 (рис.6.29,в), який має такі характеристики:
qx = q2 = 2кН м, qy = 0, lx = 0, ly = 3м,
м, qy = 0, lx = 0, ly = 3м,
обчислюємо:

6. МСЕ в формі методу переміщень |
48 |
p = - |
2 × 3 |
|
= -3 кН, |
p |
4 |
= -3 кН, |
|||
|
|||||||||
1 |
|
|
2 |
|
|
|
|
|
|
p2 |
= 0, |
|
|
|
p5 |
= 0, |
|||
p3 |
= - |
2 × 32 |
= -1,5 кНм, |
p6 |
=1,5 кНм. |
||||
12 |
|
||||||||
|
|
|
|
|
|
|
|
||
Надалі обчислимо компоненти вектора Q , беручи до уваги, що кінцеві сили із стержнів пере-
даються з на з вузли з скінченно-елементної з моделі з у зворотньому з напрямі з і з тому з повинні з братися з із
зворотнім знаком. Отже, можемо записати:
Q |
= -( p1−2 |
+ p1−4 ) = 3, |
Q |
|
= -( p1−2 + p1−4 ) = -4,8, |
Q |
|
= -( p1−2 |
+ p1−4 ) |
= 4,7, |
||||
1 |
|
1 |
1 |
2 |
|
2 |
2 |
3 |
|
3 |
3 |
|
||
Q |
|
= - p1−2 |
= 0, |
Q |
5 |
|
= - p1−2 |
= -4,8, |
Q |
6 |
|
= - p1−2 |
= -3,2, |
|
4 |
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
||
Q |
|
= - p3−5 |
= 0, |
Q |
8 |
= - p3−5 |
= -9,6, |
Q |
9 |
|
= - p3−5 |
= -12,8, |
|
|
7 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
||
Q |
|
= - p1−4 |
= 3, |
Q |
|
|
= - p1−4 |
= 0, |
Q |
|
|
= - p1−4 |
= -1,5, |
|
10 |
4 |
|
11 |
5 |
|
12 |
6 |
|
|
|||||
Q = - p3−5 |
= 0, |
Q = - p3−5 = -9,6, |
Q = - p3−5 |
=12,8. |
|
|||||||||
13 |
4 |
|
14 |
5 |
|
15 |
6 |
|
|
|||||
Таким зчином, звектор зкінцевих зсил, зякі зпередаються зна звузли зскінченно-елементної змоделі з збо-
ку завантажених стержнів, запишеться у вигляді:
|
-4,8 |
|
|
-4,8 |
-3,2 |
|
-9,6 |
-12,8 |
|
-1,5 0 |
-9,6 12,8} . |
QT = {3 |
4,7 |
0 |
0 |
3 0 |
|||||||
Зрештою вектор вузлових навантажень |
|
|
|
|
|
|
|||||
|
-4,8 |
|
|
-4,8 |
-3,2 |
|
-9,6 |
-12,8 |
|
0 -1,5 |
0 -9,6 12,8} |
FT = {3 |
4,7 |
0 |
1,8 |
4,2 |
|||||||
.
6.11.3. Побудова матриці жорсткості скінченно-елементної моделі
Матриця жорсткості скінченно-елементної моделі має такий вигляд:
K1,1 |
K1,2 |
K1,8 |
K1,15 |
|
|
|
|
|
|
|
K2,2 |
K2,8 |
K2,15 |
|
K2,1 |
|
|||
K = |
|
|
|
. |
|
|
|
|
|
|
K15,2 |
K15,8 |
K15,15 |
|
|
|
|||
K15,1 |
|
|||
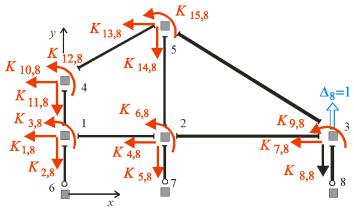
6. МСЕ в формі методу переміщень |
49 |
Для обчислення елементів матриці жорсткості K необхідно почергово надавати вільним вуз-
лам з скінченно-елементної з моделі з одиничні з переміщення з і знаходити з реакції, з які з передаються з на вузли з боку стержнів, які деформуються внаслідок цих переміщень.
Обчислимо, наприклад, елементи 8-го стовпця. Задля цього надамо дискретній моделі перемі-
щення D8 = 1, покладаючи, що всі інші вузлові переміщення дорівнюють нулю. При такій дії де-
формуються лише ті стержні, що підходять до вузла 3. Схему вузлових реакцій зображено на рис.6.30.
Рис.6.30
Реакції, які передаються на вузли, до яких прикріплено тільки недеформовані стержні, дорів-
нюють нулю, тобто:
K1,8 = K2,8 = K3,8 = K10,8 = K11,8 = K12,8 = 0.
Для обчислення інших реакцій розглянемо схему стержнів, що деформуються (рис.6.31).
На схемі враховано, що вертикальне переміщення D8 вузла 3 з скінченно-елементної з моделі з для
з
стержнів 3-5 і 3-8 є вертикальним переміщенням їхніх початків d2, а для стержня 2-3 − вертикаль-
ним переміщенням кінця d5.
Кінцеві реакції визначаються елементами відповідних матриць жорсткості: для стержнів 2-3, 3-5 − матрицею жорсткості стержня, який має затиснення на обох кінцях (перший тип), для стерж-
ня 3-8 − матрицею жорсткості стержня із затисненням на початку і шарніром на кінці (другий тип). На підставі схеми (рис.6.31) можемо записати
K |
4,8 |
= k 2−3 |
= − SC( f − |
12i |
) |
|
2−3 |
= 0; |
|
|
|
|||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
15 |
|
|
l2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2−3 |
× 0, 25 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
K |
5,8 |
= k 2−3 = (- fS 2 - |
12i |
C 2 ) |
|
|
= 0 - |
12 |
×12 = -0,0469; |
|||||||
|
|
|
||||||||||||||
|
|
35 |
|
|
l2 |
|
|
|
|
82 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
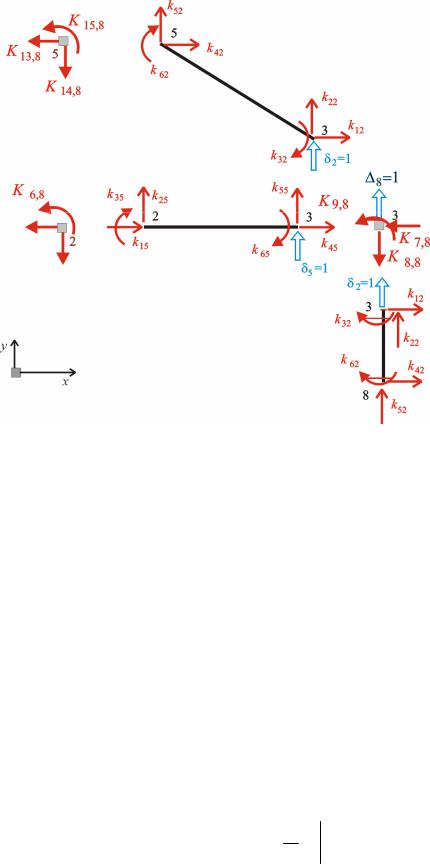
6. МСЕ в формі методу переміщень |
50 |
|
|
|
|
|
|
|
|
|
|
Рис.6.31 |
|
|
|
2-3 |
|
6i |
|
2-3 |
6 |
× 0, 25 |
×12 = 0,1875; |
|
|
|
|
|
||||||
K |
|
= k |
= |
C |
= |
|||||
6,8 |
35 |
|
|
8 |
||||||
|
|
|
l |
|
|
|
||||
|
|
|
|
|
|
|
|
|||
K |
|
= k |
2-3 |
+ k3-5 |
+ k 3-8 |
= SC( f − |
12i |
) |
|
2-3 |
+ SC( f − |
12i |
) |
|
3-5 + |
|
|
|
|||||||||||||
7,8 |
45 |
|
|
||||||||||||
|
|
12 |
12 |
|
l2 |
|
|
|
l 2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
+ SC( f − |
3i |
) |
|
3-8 |
= −9,5885; |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12i |
|
|
|
|
2 -3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
K8,8 |
= k552-3 + k322-5 + k223-8 = ( fS 2 + |
C 2 ) |
|
|
+ |
||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3-8 |
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|||
|
|
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
+ ( fS 2 + |
C 2 ) |
|
|
= 40,5956; |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= k652−3 + k323−5 + k323−8 = ( |
6i |
|
|
|
2−3 |
6i |
|
|
|
3−5 |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
K 9,8 |
C) |
|
+ (− |
C) |
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
l |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3-5 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
K13,8 = k423-5 = (−SC( f − |
12i |
)) |
|
|
= 9,5885; |
|
|||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|||||
|
12i |
|
2 -3 |
|
|
|
|||
( fS 2 + |
C 2 ) |
+ |
||
|
||||
|
l 2 |
|
||
3−8
+ (− 6i C) = 0,2835; l

6. МСЕ в формі методу переміщень |
51 |
|||||||||
|
|
3−5 |
|
|
|
|
12i |
|
3−5 |
|
|
|
|
|
|
|
|
|
|||
K |
= k |
= (− fS 2 − |
C 2 ) |
= −7, 2154; |
|
|||||
32 |
|
|
||||||||
14,8 |
|
|
|
|
|
l 2 |
|
|
||
|
|
3−5 |
|
6i |
|
3−5 |
|
|||
|
|
|
|
|
||||||
K |
= k |
= (− |
C) |
= 0,0096. |
|
|||||
62 |
|
|
||||||||
15,8 |
|
|
l |
|
|
|
|
|
||
|
|
|
|
|
|
|||||
Правильність розрахунків може бути перевірена за допомогою програми-тренажера . Якщо при
перевірці знемає зпомилок, зпрограма зрозв’яже зрівняння зрівноваги (6.47) і видасть лістинг із величи-
нами з вузлових з переміщень з скінченно-елементної з моделі (табл.6.6) з і з вказівкою з щодо з стержнів, зу-
силля в яких слід обчислити вручну.
|
|
|
Таблиця 6.6 |
|
|
|
|
№ |
DX |
DY |
DF |
|
|
|
|
1 |
6.0630880E+00 |
-1.4219720E-01 |
2.3217250E+00 |
|
|
|
|
2 |
6.0239660E+00 |
-3.3510400E-01 |
-2.7461000E-01 |
|
|
|
|
3 |
6.0933580E+00 |
-3.8669850E-01 |
-3.4268370E+00 |
|
|
|
|
4 |
6.1645700E+00 |
-1.8428430E-01 |
-2.4085670E+00 |
|
|
|
|
5 |
6.3384370E+00 |
-5.8774600E-01 |
5.3624630E+00 |
|
|
|
|
6 |
0.0000000E+00 |
0.0000000E+00 |
0.0000000E+00 |
|
|
|
|
7 |
0.0000000E+00 |
0.0000000E+00 |
0.0000000E+00 |
|
|
|
|
8 |
0.0000000E+00 |
0.0000000E+00 |
0.0000000E+00 |
|
|
|
|
Кожен рядок таблиці містить поступальні x i y, а також кутове переміщення ϕ відповідно-
го вузла, тобто компоненти вектора вузлових переміщень .
6.11.4. Обчислення зусиль у стержнях
Наступна задача розрахунку полягає в обчисленні внутрішніх зусиль в елементах споруди за формулою (6.58):
′ |
|
′ |
se |
= heδe |
+ pe . |
Виконаємо такий розрахунок для стержня 3-5. Вектор кінцевих переміщень будується на підставі
лістингу:
δT |
= {δ δ |
2 |
δ |
3 |
δ |
4 |
δ |
5 |
δ |
6 |
} |
= { |
x3 |
y3 |
ϕ3 |
x5 |
y5 |
ϕ5 |
} |
= |
3−5 |
1 |
|
|
|
|
3−5 |
|
|
3−5 |
={ 6,093358 -0,386698 -3,426837 | 6,338437 -0,587746 5,362463}.

|
|
Е в |
|
ормі мето |
|
|
|
|
перемі ен |
|
|
|
|
|
|
|
52 |
|||||||||||||||||
|
атриц |
h, |
|
ка ви начає |
|
усилл в локал ній систе і координат стержн |
по пере і |
енн |
йо |
|||||||||||||||||||||||||
о кінців у |
ло |
ал ній систе |
|
і, |
|
|
ає такий ви л д |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
12 |
|
0 |
|
16 |
12 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0,0144 |
|
|
|
|
0,0192 |
|
0,12 |
0,0144 |
0,0192 |
0,12 |
|
|
|||||||||||
|
|
h3 |
|
|
|
|
|
|
0.072 |
|
|
|
|
|
|
0,096 |
|
0,8 |
|
0,072 |
0,096 |
0,4 |
. |
|
||||||||||
|
|
5 |
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
12 |
|
0 |
|
|
16 |
12 |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0,0144 |
|
|
|
|
|
0,0192 |
|
0,12 |
|
0,0144 |
0,0192 |
0,12 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0,072 |
|
|
|
|
|
0,4 |
|
0,4 |
|
0,072 |
0,096 |
0,8 |
|
|
|||||||||
Перетвори |
|
|
о ро поділене на стержен |
навантаженн |
до локал ни |
осей координат |
а фор |
у |
||||||||||||||||||||||||||
ла и . . |
ут lx |
|
|
|
ly |
|
|
|
|
|
l |
|
sin =0,6; cos = – 0,8; qx |
та qy= – 2,4. |
|
|
||||||||||||||||||
q |
x |
qxly cos |
|
qylx |
sin |
0 |
2,4 8 |
0,6 |
1,152 |
/ ; |
|
|
|
|
||||||||||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||
qy |
|
q |
l |
y sin |
q |
|
l |
x cos |
0 |
|
2,4 |
8 |
0,8 |
1,536 |
|
/ . |
|
|
|
|||||||||||||||
|
|
|
x |
|
|
y |
|
|
10 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ви начи |
о вектор кінцеви |
сил у локал ній систе |
і координат від ро поділени навантажен |
|
||||||||||||||||||||||||||||||
p1 |
|
qxl |
|
|
|
|
( |
1,152) |
10 |
|
|
5,76 |
|
, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p2 |
|
|
qyl |
|
|
1,536 10 |
|
|
7,68 |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p3 |
|
|
qyl2 |
1,536 10 |
2 |
|
12,8 |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
12 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p4 |
|
|
qxl |
|
|
( |
1,152) |
10 |
|
5,76 |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p5 |
|
|
qyl |
|
|
1,536 10 |
|
|
7,68 |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p6 |
|
|
qyl2 |
1,536 10 |
2 |
|
12,8 |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
12 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вектор кінцеви реакцій, о числений |
а фор |
улою (6.58) остаточно |
ає ви л д |
|
|
|||||||||||||||||||||||||||||
s T ={12,095 -7,913 12,205 | -0,574 -7,447 -9,879 }.
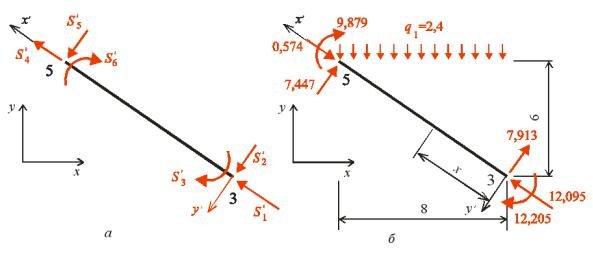
6. МСЕ в формі методу переміщень |
53 |
Отже, кінцеві зусилля в стержні 3-5 становлять: |
|
N3 = −12,085кН; |
N5 = −12,085кН; |
Q3 = −7,913кН; |
Q5 = −7,447кН; |
M3 = 12,20кН / м; |
M5 = −9,879кН / м. |
Схему кінцевих зусиль в стержні 3-5 зображено на рис. 6.32.
Рис.6.32
6.12. Особливості розрахунку просторових стержневих систем
Просторові стержневі системи на теперішній час розраховуються, як правило, за методом скін-
ченних елементів (МСЕ). Алгоритм розрахунку практично не відрізняється від алгоритму розра-
хунку плоских стержневих систем. Відмінності стосуються лише складу вузлових характеристик,
матриці перетворення і матриць жорсткості скінченних елементів.
6.12.1. Рівняння рівноваги вузлів просторових рам
Для розрахунку за методом скінченних елементів просторову стержневу систему необхідно замінити дискретною моделлю, що складається з вузлів і стержнів, які можуть бути довільно оріє-
нтовані з у з просторі. з Розташування з вузлів з скінченно-елементної з моделі з визначається за з допомогою глобальної системи декартових координат xyz. За осями цієї координатної системи орієнтуються всі статичні і кінематичні вузлові характеристики скінченно-елементної моделі.
Будь-який з вільний з жорсткий з вузол i з скінченно-елементної з моделі з має з шість з ступнів з вільності,
тобто можливість трьох поступальних переміщень по напрямах координатних осей xi, yi,
трьох кутових переміщень ϕxi, ϕyi, ϕzi цього вузла (рис.6.33,а).
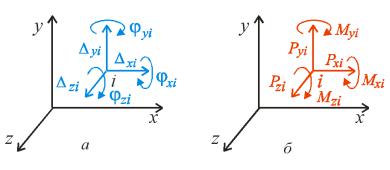
6. МСЕ в формі методу переміщень |
54 |
Рис.6.33
Означені величини можуть бути записані у вигляді вектора
Ti = { xi yi zi ϕxi ϕyi ϕzi }.
Для практичних розрахунків зручно використовувати наскрізну нумерацію компонентов вуз-
лових переміщень у межах всієї моделі. Нумерація переміщень при цьому залежатиме від номера вузла. В такому разі вектор вузлових переміщень вузла i матиме вигляд
T = { |
6i-5 6i-4 6i-3 6i-2 6i-1 6i}. |
i |
|
Сукзупність всіх вузлових переміщень скінченно-елементної моделі, яка має n жорстких вільних вузлів, становить вектор вузлових переміщень
T = { 1 2 … i … n} .
Сумарні реакції всіх стержнів, які примикають до вузла i, зобразимо у вигляді трьох зосере-
джених сил які орієнтовані за осями глобальної системи координат усієї моделі, і
трьох зосереджених моментів xi, yi, zi, які обертаються відносно зазначених координатних осей. Для вузла i ці величини можуть бути записані у вигляді вектора
RTi = { Rxi, Ryi, Rzi, xi yi zi }.
При виконанні розрахунків необхідно, щоб номери вузлових реакцій відповідали номерам ана-
логічних вузлових переміщень, тобто даний вектор може бути записаний як
RTi = {R6i-5 R6i-4 R6i-3 R6i-2 R6i-1 R6i}.
На базі векторів для всіх вільних вузлів складається повний вектор вузлових реакцій всієї скін-
ченноелементної моделі:
|
|
|
|
RT = {R1 R2 … Ri |
… Rn} . |
||
6. МСЕ в формі методу переміщень |
55 |
Зовнішнє навантаження на будь-який жорсткий вузол і може бути представлено трьома компо-
нентами зосереджених сил Pxi, Pyi, Pzi, які діють у напрямах осей глобальної системи координат, і
трьома зосередженими моментами Mxi, Myi, Mzi, що обертаються відносно відповідних осей
(рис.6.33,б). Сукупність навантажень становить вектор
FiT = { Pxi Pyi Pzi Mxi Myi Mzi}.
Якщо нумерацію компонентів цього вектора пов’язувати з нумерацією вузлів просторової сис-
теми, то вектор набирає вигляду
|
|
|
|
|
FT |
= {F1 F2 … Fi |
… Fn} . |
|
|
|
|
|
|
|
Вектор вузлових реакцій R пов’язується з вектором вузлових переміщень |
за допомогою |
|||
матриці жорсткості скінченно-елементної моделі
R = K ,
де K − матриця жорсткості скінченно-елементної моделі:
K1,1 |
K1,2 |
|
K1,i |
|
K1,n |
|
|
|
|
|
|
|
|
K2,1 |
K2,2 |
|
K2,i |
|
K2,n |
|
K = |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kn,2 |
Kn,i |
|
|
|
Kn,1 |
Kn,n |
|||||
Будь-який коефіцієнт матриці жорсткості Ki,j дорівнює вузловій реакції Ri, яка зумовлена дією примусового вузлового переміщення j = 1, за умови, що всі інші переміщення вузлів дорівню-
ють нулю:
Ki,j = Ri при j = 1, |
1= 2=...= j-1= j+1=...= n=0. |
Елементи матриці жорсткості K обчислюються через матриці жорсткості окремих стержнів.
Матричне з рівняння з рівноваги з вузлів з скінченно-елементної з моделі з нічим з не з відрізняється з від аналогічного рівняння для плоских систем:
K − F = 0 .
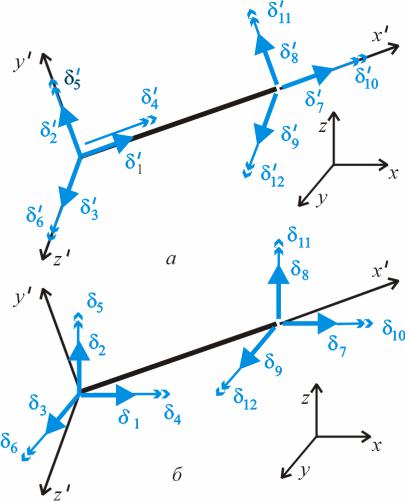
6. МСЕ в формі методу переміщень |
56 |
6.12.2. Матриця перетворення
Кінематичні і статичні характеристики на кінцях скінченного елемента (кінцеві переміщення або кінцеві реакції) можуть бути орієнтовані за осями локальної або глобальної системи коорди-
нат. На рис.6.34,а зображено кінцеві переміщення в локальній, а на рис.6.34,б − у глобальній сис-
темі координат стержня. Як і раніше, за початок локальної системи координат стержня i-j беруть кінець стержня, який є притичним до вузла з меншим номером. Будемо вважати, що i<j, тобто по-
чаток стержня знаходиться у вузлі і, а кінець − у вузлі j.
Рис.6.34
Позначення кінцевих переміщень наведено у табл.6.7.
Таблиця 6.7
Переміщення |
Система |
x |
y |
z |
ϕx |
ϕy |
ϕz |
|
координат |
||||||||
|
|
|
|
|
|
|
||
Початок i |
локальна |
δ′1 |
δ′2 |
δ′3 |
δ′4 |
δ′5 |
δ′6 |
|
глобальна |
δ1 |
δ2 |
δ3 |
δ4 |
δ5 |
δ6 |
||
|
||||||||
Кінець j |
локальна |
δ′7 |
δ′8 |
δ′9 |
δ′10 |
δ′11 |
δ′12 |
|
глобальна |
δ7 |
δ8 |
δ9 |
δ10 |
δ11 |
δ12 |
||
|
6. МСЕ в формі методу переміщень |
57 |
Аналогічно нумеруються реакції на кінцях стержня в локальній системі координат (табл.6.8):
Таблиця 6.8
Кінцеві реакції |
Система |
Rx |
Ry |
Rz |
Mx |
My |
Mz |
|
координат |
|
|
|
|
|
|
||
Початок i |
локальна |
r′1 |
r′2 |
r′3 |
r′4 |
r′5 |
r′6 |
|
глобальна |
r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
||
|
||||||||
Кінець j |
локальна |
r′7 |
r′8 |
r′9 |
r′10 |
r′11 |
r′12 |
|
глобальна |
r7 |
r8 |
r9 |
r10 |
r11 |
r12 |
||
|
Для кожного стержня просторової системи означені величини можуть бути записані у вигляді векторів:
∙ вектора кінцевих переміщень у локальній системі координат
′T |
= {δ‘1 |
δ‘2 δ‘3 ¦δ‘4 |
δ‘5 δ‘6 ¦δ‘7 δ‘8 δ‘9 ¦δ‘10 δ‘11 δ‘12}; |
δe |
∙ вектора кінцевих переміщень у глобальній системі координат
δTe = {δ1 δ2 δ3 ¦δ4 δ5 δ6 ¦δ7 δ8 δ9 ¦δ10 δ11 δ12};
∙ вектора кінцевих реакції у локальній системі координат
′T |
= {r‘1 r‘2 r‘3 ¦r‘4 |
r‘5 r‘¦r‘7 r‘8 r‘9 ¦ r‘10 r‘11 r‘12}; |
re |
∙ вектора кінцевих реакції у глобальній системі координат
reT = {r1 r2 r3 ¦r4 r5 r6 ¦ r7 r8 r9 ¦r10 r11 r12}.
Однотипні характеристики в локальній і глобальній системах координат пов’язані між собою за допомогою матриці перетворення Te :
δ′ = Teδe ,
re = Tere .
Матриця перетворень є блочною діагональною матрицею
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
Te |
= |
|
t |
, |
(6.60) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t e |
|

6. МСЕ в формі методу переміщень |
58 |
де кожний блок має вигляд
c |
c |
c |
|
|
11 |
12 |
13 |
|
|
t = c21 |
c22 |
c23 |
. |
(6.61) |
|
|
|
|
|
|
c32 |
c33 |
|
|
c31 |
|
|
Компонентами матриці t є напрямні косинуси осей локальної системи координат стержня від-
носно осей глобальної системи координат. У глобальній системі координат координати початко-
вого і кінцевого вузлів однозначно визначають положення стержня як лінійного елемента у прос-
торі і дозволяють обчислити напрямні косинуси за формулами:
c = |
x j − xi |
, |
c = |
y j − yi |
, |
c = |
z j − zi |
, |
(6.62) |
|
|
|
|||||||
11 |
lij |
|
12 |
lij |
|
13 |
lij |
|
|
|
|
|
|
|
|
|
l = |
(x |
j |
− x )2 |
+ ( y |
j |
− y )2 |
+ (z |
j |
− z |
)2 . |
(6.63) |
ij |
|
i |
|
i |
|
i |
|
|
З іншого боку, стержень як фізичне тіло має один ступінь вільності − він може обертатися від-
носно своєї поздовжньої осі x’. Тому для однозначної орієнтації осей o’y’ i o’z’ локальної системи координат стержня щодо осей глобальної системи координат необхідно додатково задати принай-
мні один параметр. Найбільш поширеним способом орієнтації локальної системи координат є за-
вдання кута чистого обертання Ψ на площині xy, який бере відлік від сліду площини y’z’ до осі o’y’ (рис.6.35).
Рис.6.35
Положення головних осей інерції o’y’ і o’z’ поперечного перерізу стержня визначається через напрямні косинуси поздовжньої осі стержня o’x’ і кут Ψ за формулами:
Е в ормі мето |
перемі ен |
59 |
|
c21 |
c11c13sin |
c12cos |
, |
|
|
|
|
|
c22 |
c12c13sin |
c11cos |
, |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
c2 |
c2 |
|
|
|
|
|
|
|
c2 |
|
c2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
11 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c11c13cos |
c12 |
sin , |
|
||||||||||||
|
c |
|
c2 |
c2 sin , |
|
|
|
|
|
|
|
|
c |
(6.64) |
|||||||||||||||||||||||||||||||
|
23 |
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
c2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
|
|||
|
|
c12c13sin |
c11 |
cos , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
c |
c |
|
|
c2 |
c2 |
|
cos . |
|
|
|||||||||||||||||||||||||||||||||||
|
32 |
|
|
|
c2 |
c2 |
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
11 |
12 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
11 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нши спосо о |
орієнтаці |
осей o’y’, o’z’ стержн є авдаванн |
координат довіл но о рано ре |
||||||||||||||||||||||||||||||||||||||||||
перно точки, |
о ро ташована в додатній півпло |
ині x’y’. |
|
ц о у випадку напр |
ні косинуси |
||||||||||||||||||||||||||||||||||||||||
ви начают с |
і векторни |
співвідношен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
c12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c13k |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
e1 c11i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
er |
(xr |
|
|
|
|
(yr |
yi ) |
|
(zr |
|
|
|
, |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
zi )k |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
xi )i |
j |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
e |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
e1 |
er |
|
, |
|
|
|
|
|
|
(6.65) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c k |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
c i |
j |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
3 |
|
31 |
|
|
|
|
|
32 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
e1 |
er |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
e2 |
|
c22 |
|
|
|
e3 e1. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c23k |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
c21i |
j |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
6.13. Матриця жорсткості просторового стержня
атриц жорсткості просторово о стержн |
ає ро |
|
від одно рупи еле |
ентів, о ви начают в |
ок іж |
по довжній дефор |
аці , крученні, ині стержн |
в пло |
ірніст |
і |
істит |
не алежні одна |
кінцеви |
и реакці |
и і пере |
і енн и при |
ина x’y’ і x’z’. |
|
|
|
|
k1,1 |
k1,2 |
k1,3 |
k1,4 |
k1,5 |
k1,6 |
k1,7 |
k1,8 |
k1,9 |
k1,10 |
k1,11 |
k1,12 |
|
|
k2,1 |
k2,2 |
k2,3 |
k2,4 |
k2,5 |
k2,6 |
k2,7 |
k2,8 |
k2,9 |
k2,10 |
k2,11 |
k2,12 |
|
|
k3,1 |
k3,2 |
k3,3 |
k3,4 |
k3,5 |
k3,6 |
k3,7 |
k3,8 |
k3,9 |
k3,10 |
k3,11 |
k3,12 |
|
|
k4,1 |
k4,2 |
k4,3 |
k4,4 |
k4,5 |
k4,6 |
k4,7 |
k4,8 |
k4,9 |
k4,10 |
k4,11 |
k4,12 |
|
|
k5,1 |
k5,2 |
k5,3 |
k5,4 |
k5,5 |
k5,6 |
k5,7 |
k5,8 |
k5,9 |
k5,10 |
k5,11 |
k5,12 |
|
ke |
k6,1 |
k6,2 |
k6,3 |
k6,4 |
k6,5 |
k6,6 |
k6,7 |
k6,8 |
k6,9 |
k6,10 |
k6,11 |
k6,12 |
|
k7,1 |
k7,2 |
k7,3 |
k7,4 |
k7,5 |
k7,6 |
k7,7 |
k7,8 |
k7,9 |
k7,10 |
k7,11 |
k7,12 |
||
|
|||||||||||||
|
k8,1 |
k8,2 |
k8,3 |
k8,4 |
k8,5 |
k8,6 |
k8,7 |
k8,8 |
k8,9 |
k8,10 |
k8,11 |
k8,12 |
|
|
k9,1 |
k9,2 |
k9,3 |
k9,4 |
k9,5 |
k9,6 |
k9,7 |
k9,8 |
k9,9 |
k9,10 |
k9,11 |
k9,12 |
|
|
k10,1 |
k10,2 |
k10,3 |
k10,4 |
k10,5 |
k10,6 |
k10,7 |
k10,8 |
k10,9 |
k10,10 |
k10,11 |
k10,12 |
|
|
k11,1 |
k11,2 |
k11,3 |
k11,4 |
k11,5 |
k11,6 |
k11,7 |
k11,8 |
k11,9 |
k11,10 |
k11,11 |
k11,12 |
|
|
k12,1 |
k12,2 |
k12,3 |
k12,4 |
k12,5 |
k12,6 |
k12,7 |
k12,8 |
k12,9 |
k12,10 |
k12,11 |
k12,12 e |
Е в ормі мето |
перемі ен |
60 |
|
Еле |
енти першо о стовпц |
|
|
атриці є кінцеви |
и реакці |
и стержн , |
кі |
у овлени и кінцеви |
|||||||||||||||||||||||||||||||||||||||||
пере і |
енн |
1, дру о о |
|
кінцеви |
пере |
і |
енн |
|
|
2 |
|
1 і т.д. Еле |
енти першо о р дка |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
це кінцеві опорні реакці |
r1 |
від дій кінцеви |
пере |
і |
ен , |
дру о о |
|
опорні реакці |
r2 то о. Отже, |
|||||||||||||||||||||||||||||||||||||||||
уд - кий еле |
ент |
атриці жорсткості kij |
|
|
|
це кінцева реакці ri |
, |
о |
у |
овлена кінцеви пере |
||||||||||||||||||||||||||||||||||||||||
і |
енн |
|
|
j |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Переважна |
|
іл шіст |
еле |
|
ентів |
|
|
атриці жорсткості дорівнює нулю. |
аведе о тіл ки ті еле ен |
||||||||||||||||||||||||||||||||||||||||
ти, |
кі від |
інні від нул |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
k |
|
|
k |
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
EA |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
7,7 |
|
|
|
|
7,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1,1 |
|
|
|
1,7 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k2,2 |
k8,8 |
|
|
k2,8 |
|
|
k8,2 |
|
|
|
|
|
12EIz |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k3,3 |
k9,9 |
|
k3,9 |
|
|
k9,3 |
|
|
|
12EI y |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k |
4,4 |
k |
|
|
|
|
k |
4,10 |
|
|
k |
|
|
|
|
|
|
|
GI |
|
р |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
10,10 |
|
|
|
|
|
|
|
10,4 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
5,5 |
k |
|
|
|
4EI y |
|
, |
|
|
k |
6,6 |
|
|
k |
|
|
|
|
|
|
4EI |
z |
, |
|
|
|
|
|
|
|
|
|
|
(6.66) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
11,11 |
|
|
|
l |
|
|
|
|
|
|
12,12 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k |
2,6 |
k |
2,12 |
k |
8,12 |
|
k |
6,2 |
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
k |
6,8 |
|
|
k |
8,6 |
|
6EIz |
|
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
12,2 |
|
12,8 |
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
9,11 |
k |
5,9 |
|
|
k |
3,5 |
|
|
k |
3,11 |
|
|
|
|
|
k |
|
|
|
k |
9,5 |
|
|
k |
5,3 |
|
|
|
k |
|
|
6EI y |
, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11,9 |
|
|
|
|
|
|
|
|
|
|
|
|
11,3 |
|
|
l2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k |
5,11 |
k |
6,12 |
|
k |
|
|
|
k |
|
|
|
|
|
|
2EI y |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
11,5 |
|
|
12,6 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
атриц |
жорсткості ke |
просторово о стержн |
в |
ло ал ній систе |
і координат |
оже ути оде |
|||||||||||||||||||||||||||||||||||||||||||
ржана, |
к і дл |
|
стержн |
|
на пло |
|
ині, |
|
|
а допо |
|
о ою співвідношенн |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ke |
|
|
TeT keTe . |
|
|
|
|
|
|
|
|
|
|
(6.67) |
||||||||||
6.14. Приклад розрахунку просторової рами методом скінченних елементів |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ано ро ра ункова |
одел |
|
просторово |
ра |
и |
рис. 11.36), всі стержні |
ко |
ают жорскісні |
|||||||||||||||||||||||||||||||||||||||||
пара етри |
А 300 , |
EI y EIz |
|
GI р |
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||

6. МСЕ в формі методу переміщень |
61 |
Рис.6.36
Необхідно: Визначити внутрішні зусилля в стержнях рами.
Розв’язуватимемо задачу в глобальній системі координат OXYZ (рис. 11.37). Просторову раму розглядатимемо як сукупність трьох стержневих скінченних елементів 1-2, 2-3, 3-4, поєднаних між собою у вузлах 2, 3 і з диском „ земля” жорсткими в’язями 1 та 4. З кожним скінченним елементом пов’яжемо локальні системи координат xi − j yi − j zi − j .
Рис.6.37
Вузли рами мають дванадцять можливих переміщень (рис. 11.28)
T = { 1 |
2 ... |
12} . |
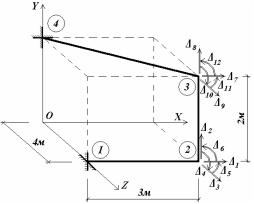
6. МСЕ в формі методу переміщень |
62 |
Рис.6.38
Система розв’язувальних рівнянь методу скінченних елементів у формі переміщень має вигляд
К × - Р = 0 ,
або в координатній формі
К1,1 |
К1,2 |
К1.3 |
К1,4 |
К1,5 |
К1,6 |
|
К1,7 |
К1,8 |
К1,9 |
К1,10 |
К1,11 |
К1,12 |
|
1 |
|
Р1 |
|
0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К2,1 |
К2,2 |
К2,3 |
К2,4 |
К2,5 |
К2,6 |
|
К2,7 |
К2,8 |
К2,9 |
К2,10 |
К2,11 |
К2,12 |
2 |
|
|
Р2 |
|
0 |
|
|||||||||||||||||||||||||||
|
К |
|
К |
|
К |
|
К |
|
К |
|
К |
|
|
К |
|
К |
|
К |
|
К |
|
К |
|
К |
|
|
|
|
|
Р |
|
0 |
|
||||||||||||||
|
|
|
3,1 |
|
|
3,2 |
|
|
3,3 |
|
|
3,4 |
|
|
3,5 |
|
|
3,6 |
|
|
|
3,7 |
|
|
3,8 |
|
|
3,9 |
|
|
3,10 |
|
|
3,11 |
|
|
3,12 |
|
3 |
|
|
3 |
|
|
|
|
|
|
К4,1 |
К4,2 |
К4,3 |
К4,4 |
К4,5 |
К4,6 |
|
К4,7 |
К4,8 |
К4,9 |
К4,10 |
К4,11 |
К4,12 |
4 |
|
|
Р4 |
|
0 |
|
|||||||||||||||||||||||||||
К |
5,1 |
К |
5,2 |
К |
5,3 |
К |
5,4 |
К |
5,5 |
К |
5,6 |
|
К |
5,7 |
К |
5,8 |
К |
5,9 |
К |
5,10 |
К |
5,11 |
К |
5,12 |
|
5 |
|
|
Р5 |
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
К6,1 |
К6,2 |
К6,3 |
К6,4 |
К6,5 |
К6,6 |
|
К6,7 |
К6,8 |
К6,9 |
К6,10 |
К6,11 |
К6,12 |
|
6 |
|
Р6 |
|
0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
К7,1 |
К7,2 |
К7,3 |
К7,4 |
К7,5 |
К7,6 |
|
К7,7 |
К7,8 |
К7,9 |
К7,10 |
К7,11 |
|
|
|
|
Р7 |
|
||||||||||||||||||||||||||||||
|
|
К7,12 |
7 |
|
|
|
0 |
|
|||||||||||||||||||||||||||||||||||||||
|
К |
|
К |
|
К |
|
К |
|
К |
|
К |
|
|
К |
|
К |
|
К |
|
К |
|
К |
|
К |
|
|
|
|
|
Р |
|
0 |
|
||||||||||||||
|
|
|
8,1 |
|
|
8,2 |
|
|
8,3 |
|
|
8,4 |
|
|
8,5 |
|
|
8,6 |
|
|
|
8,7 |
|
|
8,8 |
|
|
8,9 |
|
|
8,10 |
|
|
8,11 |
|
|
8,12 |
|
8 |
|
|
8 |
|
|
|
|
|
|
К9,1 |
К9,2 |
К9,3 |
К9,4 |
К9,5 |
К9,6 |
|
К9,7 |
К9,8 |
К9,9 |
К9,10 |
К9,11 |
К9,12 |
9 |
|
Р9 |
|
0 |
|
||||||||||||||||||||||||||||
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
К |
|
|
|
|
|
Р |
|
0 |
|
|||
|
|
10,1 |
|
10,2 |
|
10,3 |
|
10,4 |
|
10,5 |
|
10,6 |
|
|
10,7 |
|
10,8 |
|
10,9 |
|
10,10 |
|
10,11 |
|
10,12 |
|
10 |
|
10 |
|
|
|
|
|
|||||||||||||
|
К11,1 |
К11,2 |
К11,3 |
К11,4 |
К11,5 |
К11,6 |
|
К11,7 |
К11,8 |
К11,9 |
К11,10 |
К11,11 |
К11,12 |
11 |
|
Р11 |
|
0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К12,1 |
К12,2 |
К12,3 |
К12,4 |
К12,5 |
К12,6 |
|
К12,7 |
К12,8 |
К12,9 |
К12,10 |
К12,11 |
К12,12 |
12 |
Р12 |
|
0 |
|
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Вектор вузлових навантажень на скінченно-елементну модель
|
|
1 |
|
|
0 |
|
|
|
P |
|
|
|
|
|
|
|
||||
|
P |
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
P3 |
0 |
||||
|
P |
|
|
0 |
|
|
|
|
4 |
|
|
|
|
|
P |
|
|
0 |
|
|
|
|
5 |
|
|
|
|
|
P |
|
|
0 |
|
|
|
|
6 |
|
|
|
|
Р = |
|
|
= |
|
|
|
|
|
|||||
|
|
|||||
|
P7 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
P |
|
− 10 |
|||
|
|
8 |
|
|
|
|
|
P9 |
0 |
||||
|
P |
|
|
0 |
|
|
|
|
10 |
|
|
|
|
|
P |
|
|
0 |
|
|
|
|
11 |
|
|
|
|
|
P |
|
|
0 |
|
|
|
|
12 |
|
|
|
|
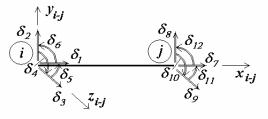
6. МСЕ в формі методу переміщень |
63 |
Для побудови матриці жорсткості всієї моделі К визначимо матриці жорсткості кожного скін-
ченного елемента в локальній k′ і в глобальній k системах координат. Стержень, що деформу-
ється в просторі, має дванадцять можливих вузлових переміщень δ1, ..., δ12 (рис.6.39).
Рис.6.39
При такій схемі розміщення невідомих переміщень матриця жорсткості окремого стержневого
скінченого елемента довжиною L в локальній системі координат будується по схемі
|
|
|
|
|
|
|
|
k′е |
= |
k1′ |
k′3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
′T |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в якій блоки мають наповнення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
12EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI |
|
|
|
|
||||
|
|
|
0 |
|
z |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
z |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
L3 |
|
|
|
|
12EI y |
|
|
|
|
|
|
|
|
|
6EI y |
|
|
|
L2 |
|
|
|
|
|||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
|
− |
|
0 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||
k′ |
= |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
GIкр |
|
L |
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
6EI y |
|
|
|
|
4EI y |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
6EI z |
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
L |
|
|
|
4EI z |
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
EA |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
12EI z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 − |
6EI z |
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
L3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
12EI y |
|
|
|
6EI y |
|
|
|
L2 |
|
|
|
|
|||||||||||||
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||
k′2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
GIкр |
L |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI y |
|
|
|
|
|
|
4EI y |
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
6EI z |
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
L |
|
4EI z |
|
|
|
|
||||||||
|
|
|
0 − |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. МСЕ в формі методу переміщень |
64 |
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|||
L |
|
|
|
|
|
|
||||||||||||||||
|
|
|
12EI z |
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI z |
|
|
|||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|||||||
|
|
L3 |
|
|
|
|
|
L2 |
||||||||||||||
|
|
|
|
|
|
12EI y |
|
|
|
|
|
6EI y |
|
|
||||||||
|
0 |
|
0 |
|
− |
|
0 |
|
− |
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
L3 |
|
|
L2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
k′3 = |
|
|
|
|
|
|
|
|
|
|
|
GI |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
− |
кр |
|
|
0 |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
L |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
6EI y |
|
|
|
|
2EI y |
|
|
|
||||||
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
6EI z |
|
|
|
L |
|
|
|
|
|
L |
2EI z |
|
|||||
|
0 |
− |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
||||||
L2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
||
Використовуючи приведену схему, отримуємо матриці жорсткості скінченних елементів в ло-
кальних системах координат
|
|
100 |
0 |
|
0 |
0 |
0 |
0 |
|
|
−100 |
0 |
|
0 |
0 |
|
0 |
0 |
|
|
||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
0 |
1,333 |
0 |
0 |
0 |
2 |
|
0 |
−1,333 |
0 |
0 |
|
0 |
2 |
|
|
||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
0 |
0 |
1,333 |
0 |
− 2 |
0 |
|
0 |
0 |
−1,333 |
0 |
− 2 |
0 |
|
|
|||||||
|
|
|
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
|
0 |
−1 0 |
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
0 |
0 |
− 2 |
0 |
4 |
0 |
|
0 |
0 |
|
2 |
0 |
|
2 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|||
k′ |
= |
0 |
2 |
|
0 |
0 |
0 |
4 |
|
0 |
|
0 |
0 |
|
0 |
2 |
, |
|
||||||
|
0 |
|
0 |
0 |
0 |
0 |
|
100 |
0 |
|
0 |
0 |
|
0 |
0 |
|
||||||||
1−2 |
|
−100 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
−1,333 |
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
0 |
0 |
0 |
|
0 |
1,333 |
|
0 |
0 |
|
0 |
− 2 |
|
||||||||
|
|
|
0 |
0 |
−1,333 |
0 |
2 |
0 |
|
0 |
0 |
1,333 |
0 |
|
2 |
0 |
|
|
||||||
|
|
|
|
|
|
|
−1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
0 |
|
0 |
|
0 |
0 |
|
0 |
1 |
|
0 |
0 |
|
|||||||||
|
|
|
0 |
0 |
− 2 |
0 |
2 |
0 |
|
0 |
0 |
|
2 |
0 |
|
4 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
0 |
2 |
|
0 |
0 |
0 |
2 |
|
0 |
− 2 |
|
0 |
0 |
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−150 |
|
|
|
|
|
|
|
|
|||||
|
|
150 |
0 |
0 |
0 |
0 |
|
0 |
|
|
0 |
|
0 |
0 |
|
0 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
0 |
4,5 |
0 |
0 |
0 |
|
4,5 |
|
|
0 |
− 4,5 |
0 |
0 |
|
0 |
|
4,5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
0 |
4,5 |
0 |
− 4,5 |
0 |
|
|
0 |
0 |
− 4,5 |
0 |
− 4,5 |
0 |
|
|
|
|||||
|
|
|
0 |
0 |
0 |
1,5 |
0 |
|
0 |
|
|
0 |
0 |
|
0 |
−1,5 |
0 |
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
0 |
− 4,5 |
0 |
6 |
|
0 |
|
|
0 |
0 |
|
4,5 |
0 |
|
3 |
|
0 |
|
|
|
|
|
|
|
0 |
4,5 |
0 |
0 |
0 |
|
6 |
|
|
0 |
− 4,5 |
0 |
0 |
|
0 |
|
3 |
|
|
|
||
k′2−3 = |
|
|
|
|
|
|
|
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
−150 |
0 |
0 |
0 |
0 |
|
0 |
|
|
150 |
0 |
|
0 |
0 |
|
0 |
|
0 |
|
||||||
|
|
|
|
− 4,5 |
|
|
|
− 4,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
0 |
0 |
0 |
|
|
0 |
4,5 |
|
0 |
0 |
|
0 |
|
− 4,5 |
|
||||||
|
|
|
0 |
0 |
− 4,5 |
0 |
4,5 |
0 |
|
|
0 |
0 |
|
4,5 |
0 |
|
4,5 |
0 |
|
|
|
|||
|
|
|
|
|
|
−1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
|
|
0 |
0 |
|
0 |
1,5 |
|
0 |
|
0 |
|
|
|
||
|
|
|
0 |
0 |
− 4,5 |
0 |
3 |
|
0 |
|
|
0 |
0 |
|
4,5 |
0 |
|
6 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 |
4,5 |
0 |
0 |
0 |
|
3 |
|
|
0 |
− 4,5 |
0 |
0 |
|
0 |
|
6 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
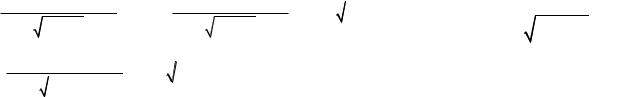
Е в ормі мето |
перемі ен |
65 |
|
60 |
0 |
0 |
0 |
0 |
0 |
|
60 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
||||||||||||
|
0 |
0,288 |
0 |
0 |
0 |
0,72 |
|
0 |
0,288 |
0 |
0 |
0 |
0,72 |
|
|
0 |
0 |
0,288 |
0 |
0,72 |
0 |
|
0 |
0 |
0,288 |
0 |
0,72 |
0 |
|
|
0 |
0 |
0 |
0,6 |
0 |
0 |
|
0 |
0 |
0 |
0,6 |
0 |
0 |
|
|
0 |
0 |
0,72 |
0 |
2,4 |
0 |
|
0 |
0 |
0,72 |
0 |
1,2 |
0 |
|
k3 4 |
0 |
0,72 |
0 |
0 |
0 |
2,4 |
|
0 |
0,72 |
0 |
0 |
0 |
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
0 |
0 |
0 |
0 |
0 |
|
60 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
||||||||||||
|
0 |
0,288 |
0 |
0 |
0 |
0,72 |
|
0 |
0,288 |
0 |
0 |
0 |
0,72 |
|
|
0 |
0 |
0,288 |
0 |
0,72 |
0 |
|
0 |
0 |
0,288 |
0 |
0,72 |
0 |
|
|
0 |
0 |
0 |
0,6 |
0 |
0 |
|
0 |
0 |
0 |
0,6 |
0 |
0 |
|
|
0 |
0 |
0,72 |
0 |
1,2 |
0 |
|
0 |
0 |
0,72 |
0 |
2,4 |
0 |
|
|
0 |
0,72 |
0 |
0 |
0 |
1,2 |
|
0 |
0,72 |
0 |
0 |
0 |
2,4 |
|
атриц перетворенн тр о ви ірно систе |
и координат ає ви л д |
||||
|
t |
0 |
0 |
0 |
|
Т |
0 |
t |
0 |
0 |
, |
0 |
0 |
t |
0 |
|
|
|
0 |
0 |
0 |
t |
|
Однотипні локи атриці перетворенн |
ают |
ко |
поненти |
||
lx mx nx
t ly my ny , lz mz nz
котрі ожна ви начити а фор ула и
lx |
X j |
Xi |
; |
|
mx |
|
|
|
Yj |
|
Yi |
; |
nx |
Z j |
Zi |
; |
|
|
|
|||
Li |
|
|
|
|
|
Li |
|
|
Li |
|
|
|
|
|||||||||
|
j |
|
|
|
|
|
|
j |
|
|
j |
|
|
|
|
|||||||
ly |
lx nx sin |
|
mx |
|
cos |
; my |
nx mx sin |
|
lx |
cos |
; ny |
|||||||||||
|
|
l2 |
|
m2 |
|
|
|
|
l2 |
m2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
mx nx cos |
lx sin |
; nz |
|
|
|
|
|
. |
|
||||||||||||
|
2 |
2 |
|
|
|
|||||||||||||||||
mz |
|
|
|
|
|
|
|
|
|
|
|
|
lx |
mx |
cos |
|
||||||
|
|
|
l |
2 |
m2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
sin ; lz |
lx nx cos |
mx |
sin ; |
||
lx2 mx2 |
||||||
|
l2 |
|
||||
|
|
|
m2 |
|||
|
|
|
x |
x |
||
В ци фор ула |
по начено Xi , Yi , Zi , X j , Yj , Z j – координати початково о і кінцево о ву лів |
||
скінченно о еле |
енту в ло ал ній систе і координат, – кут іж віссю yi j і пр ою перетину |
||
пло |
ин XY та yi |
j zi |
j . |
|
л стержн |
-2: |
|
|
0; |
|
|
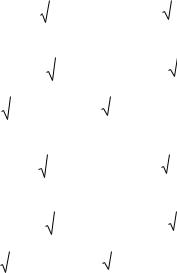
|
|
|
|
|
|
Е в |
|
|
|
|
|
|
ормі мето |
|
|
|
|
|
|
|
перемі ен |
|
|
|
|
|
|
|
|
|
66 |
||||||||||||||||||||||||
lx |
X2 |
X1 |
3 |
0 |
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
L1 |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
mx |
|
|
Y2 |
Y1 |
|
|
0 |
0 |
|
|
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
L1 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
nx |
|
Z2 |
Z1 |
|
|
4 |
4 |
|
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
L1 |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ly |
|
|
|
lxnx sin |
mx cos |
|
1 0 0 |
|
0 1 |
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lx2 |
mx2 |
|
|
|
|
|
|
|
|
|
|
|
12 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
my |
|
|
|
|
|
nxmx sin |
lx cos |
|
0 |
0 |
0 |
1 1 |
1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
lx2 |
mx2 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ny |
|
|
|
|
lx2 |
mx2 sin |
12 |
|
02 |
0 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
lz |
|
|
|
lxnx cos |
mx sin |
1 0 1 |
|
0 0 |
|
|
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lx2 mx2 |
|
|
|
|
|
|
|
|
|
|
|
12 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
mz |
|
|
|
|
|
mxnx cos |
|
lx sin |
|
0 |
0 1 |
1 0 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
lx2 |
mx2 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
nz |
|
|
|
|
lx2 |
mx2 cos |
12 |
|
02 |
1 |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
атриц |
перетворенн |
систе |
|
|
и координат на уває ви л ду |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
1 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
1 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
0 |
0 |
0 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
0 |
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|||||||||||
лстержн 2-3:
0 ;
lx |
X3 |
X2 |
3 |
|
3 |
0 |
; |
||||||
|
L2 |
3 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
mx |
|
Y3 |
Y2 |
2 |
|
0 |
|
1 |
; |
|
|||
|
L2 |
3 |
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
Е в |
|
|
ормі мето |
|
|
перемі ен |
|
|
|
|
|
|
|
|
67 |
||||||||||||||||||||
nx |
Z3 |
Z2 |
4 |
4 |
|
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
L2 |
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ly |
|
lx nx sin |
mx cos |
0 0 0 |
1 1 |
1; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
l2 |
m2 |
|
|
|
|
|
|
|
02 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
my |
|
nx mx sin lx |
cos |
0 1 0 |
0 1 |
0 |
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
l2 |
m2 |
|
|
|
|
|
|
|
02 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n |
y |
|
l2 |
m2 |
|
02 |
12 |
|
0 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lz |
|
lx nx cos |
mx sin |
|
|
|
0 0 1 |
1 0 |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
l2 |
m2 |
|
|
|
|
|
|
|
02 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
mz |
|
mx nx cos lx |
sin |
1 0 1 |
0 0 |
0 |
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
l2 |
m2 |
|
|
|
|
|
|
|
02 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
nz |
|
lx2 |
mx2 |
|
02 |
12 |
|
1 |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
атриц |
перетворенн |
систе |
и координат на уває ви л ду |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
1 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
Т2 |
3 |
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
1 |
0 |
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
1 |
||||
лстержн 3-4:
0 ;
lx |
X4 |
X3 |
0 3 |
|
|
0,6 |
; |
|
|
|
|
||||||||||
|
|
L3 |
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
mx |
|
|
Y4 |
Y3 |
2 |
2 |
|
|
0 |
; |
|
|
|
|
|
||||||
|
|
L3 |
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
nx |
|
Z4 |
Z3 |
0 |
4 |
|
|
0,8 |
; |
|
|
|
|
||||||||
|
|
L3 |
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ly |
|
|
lx nx sin |
mx cos |
0,6 0,8 |
0 0 1 |
0 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
lx2 |
mx2 |
|
|
0,6 2 |
02 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
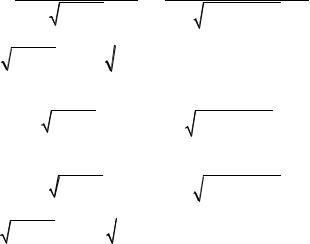
|
|
|
Е в |
|
ормі мето |
перемі ен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
||||||||||||||||||||||||||||
my |
|
nx mx sin |
lx cos |
0,8 |
|
0 0 |
|
0,6 |
1 |
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
lx2 mx2 |
|
|
|
|
|
|
|
|
|
0,6 |
2 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
0,6 2 |
|
|
|
|
|
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n |
y |
|
l2 |
m2 |
|
|
|
|
|
|
|
|
02 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lz |
|
lx nx cos |
mx sin |
|
|
|
0,6 |
|
|
0,8 1 |
0 0 |
|
0,8; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
lx2 mx2 |
|
|
|
|
|
|
|
|
|
0,6 2 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
mz |
|
mx nx cos |
|
lx sin |
0 |
|
|
|
0,8 1 |
|
|
0,6 |
0 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
lx2 mx2 |
|
|
|
|
|
|
|
|
|
0,6 |
2 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
0,6 2 |
|
|
|
|
|
|
0,6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
z |
|
l2 |
m2 |
|
|
|
|
|
|
|
|
02 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
атриц перетворенн систе |
и координат на уває ви л ду |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 0 0,8 |
|
|
0 0 |
|
0 |
|
|
0 0 |
0 |
|
|
0 0 |
|
|
|
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
0 |
|
|
0 |
0 |
|
0 |
|
|
0 |
0 |
0 |
|
|
0 |
0 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8 0 0,6 |
|
|
0 0 |
|
0 |
|
|
0 0 |
0 |
|
|
0 0 |
|
|
|
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
0,6 0 0,8 |
|
|
0 0 |
0 |
|
|
0 0 |
|
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
1 |
|
0 |
|
|
0 |
0 |
0 |
|
|
0 |
0 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
. T3 |
4 |
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
|
|
0,8 0 0,6 |
|
|
0 0 |
0 |
|
|
0 0 |
|
|
|
0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
|
|
0 0 |
|
0 |
0,6 0 0,8 |
|
|
0 0 |
|
|
|
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
0 |
|
0 |
|
|
0 |
1 |
0 |
|
|
0 |
0 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
|
|
0 0 |
|
0 |
|
0,8 0 0,6 |
|
|
0 0 |
|
|
|
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
|
|
0 0 |
|
0 |
|
|
0 0 |
0 |
0,6 0 0,8 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
0 |
|
0 |
|
|
0 |
0 |
0 |
|
|
0 |
1 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
0 |
|
|
0 0 |
|
0 |
|
|
0 0 |
0 |
|
0,8 0 0,6 |
|
|
|||||||||||||||
|
|
|
атриці жорсткості скінченни |
|
еле |
ентів в |
ло ал ній систе і координат |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 2 Т1 2k1 2Т1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 0 0 |
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
100 |
0 |
|
0 |
|
0 |
0 |
0 |
|
100 |
0 |
|
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 1 0 |
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
0 |
1,333 |
|
0 |
|
0 |
0 |
2 |
|
0 |
1,333 |
|
0 |
|
|
0 |
0 |
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 1 |
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
0 |
0 |
1,333 |
0 |
2 |
0 |
|
0 |
0 |
|
1,333 |
|
|
0 |
2 |
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
1 |
0 |
0 |
|
0 |
0 |
|
0 |
|
|
1 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
1 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 1 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
0 |
0 |
|
2 |
|
0 |
4 |
0 |
|
0 |
0 |
|
2 |
|
|
0 |
2 |
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 1 |
|
0 0 0 |
|
0 0 0 |
|
|
|
0 |
2 |
|
0 |
|
0 |
0 |
4 |
|
0 |
2 |
|
0 |
|
|
0 |
0 |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
1 0 0 |
|
0 0 0 |
|
|
|
100 |
0 |
|
0 |
|
0 |
0 |
0 |
|
100 |
0 |
|
0 |
|
|
0 |
0 |
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 1 0 |
|
0 0 0 |
|
|
|
0 |
1,333 |
|
0 |
|
0 |
0 |
2 |
|
0 |
1,333 |
|
0 |
|
|
0 |
0 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 1 |
|
0 0 0 |
|
|
|
0 |
0 |
|
1,333 |
0 |
2 |
0 |
|
0 |
0 |
1,333 |
|
|
0 |
2 |
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
1 0 0 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
1 |
0 |
0 |
|
0 |
0 |
|
0 |
|
|
1 |
0 |
0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
0 1 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
2 |
|
0 |
2 |
0 |
|
0 |
0 |
|
2 |
|
|
0 |
4 |
0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
0 |
|
0 |
0 |
2 |
|
0 |
2 |
|
0 |
|
|
0 |
0 |
4 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||

6. МСЕ в формі методу переміщень |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
100 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
−100 |
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 |
|
|
|
|
|
|
0 |
1,333 |
|
|
0 |
|
0 |
|
0 |
|
|
2 |
|
|
|
0 |
−1,333 |
|
0 |
|
0 |
|
0 |
|
2 |
|||||||||||||||||||||||
|
0 1 0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
0 0 1 |
0 0 0 |
|
0 0 0 |
|
0 0 |
0 |
|
|
|
|
0 |
0 |
|
1,333 |
|
0 |
− 2 |
0 |
|
|
|
0 |
|
0 |
|
|
−1,333 |
|
0 |
− 2 |
0 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 0 0 |
|||||||||
|
|
|
|
|
|
1 0 0 |
|
0 0 0 |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
0 |
|
1 0 0 |
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|
||||||||||||||||||||||||||
|
0 0 0 |
|
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
0 0 0 |
0 1 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
|
0 |
0 |
|
|
− 2 |
|
0 4 0 |
|
|
|
0 |
|
0 |
|
|
|
|
2 |
|
0 2 0 |
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
0 0 1 |
|
0 0 0 |
|
|
|
|
|
|
|
= |
|
|
0 |
2 |
|
|
|
0 |
|
0 0 4 |
|
|
|
0 |
|
− 2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||||||||||
× 0 0 0 |
|
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
0 0 0 |
0 0 0 |
|
1 0 0 |
|
0 0 0 |
|
|
|
|
−100 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
100 |
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 0 0 |
|
0 1 0 |
|
0 0 |
|
|
|
|
|
|
|
0 |
−1,333 |
|
|
0 |
|
0 |
|
0 |
|
|
− 2 |
|
|
0 |
|
1,333 |
|
0 |
|
0 |
|
0 |
|
|
||||||||||||||||||||||
|
0 0 0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
||||||||||||||||||||||||||||||||||||||||||
|
0 0 0 |
0 0 0 |
|
0 0 1 |
|
0 0 0 |
|
|
|
|
0 |
0 |
|
−1,333 |
|
0 |
|
2 |
|
|
0 |
|
|
|
0 |
|
0 |
1,333 |
|
0 |
|
2 |
|
0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 0 0 |
0 0 0 |
|
0 0 0 |
|
1 0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
0 |
|
|
|
0 |
|
−1 0 0 |
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|
1 0 0 |
|||||||||||||||||||||||||||||||||||||
|
0 0 0 |
0 0 0 |
|
0 0 0 |
|
0 1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
− 2 |
|
0 2 0 |
|
|
|
0 |
|
0 |
|
|
|
|
2 |
|
0 4 0 |
|||||||||||||||||
|
0 0 0 |
0 0 0 |
|
0 0 0 |
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
0 |
|
0 0 2 |
|
|
|
0 |
|
− 2 |
|
|
|
|
0 |
|
0 0 4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2−3= ТТ2−3k′2−3Т2−3 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 −1 0 |
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
150 |
|
0 |
0 |
|
|
0 |
0 |
|
|
0 |
|
|
−150 |
0 |
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
0 |
|
|
|
4,5 |
0 |
|
|
0 |
0 |
|
|
4,5 |
|
|
0 |
|
|
− 4,5 |
0 |
|
|
0 |
|
0 |
|
|
4,5 |
|
|
|
||||||||||||||||||
1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
0 0 1 |
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
|
0 |
|
|
|
0 |
4,5 |
|
0 |
− 4,5 |
0 |
|
|
|
0 |
|
|
|
0 |
− 4,5 |
|
|
0 |
|
− 4,5 |
0 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
0 0 0 |
|
0 −1 0 |
|
0 0 0 |
|
0 0 0 |
|
|
|
0 |
|
|
|
0 |
0 |
|
1,5 |
0 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
−1,5 |
0 |
|
|
0 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 0 0 |
|
0 0 0 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
− 4,5 |
|
0 |
6 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
4,5 |
|
|
0 |
|
3 |
|
|
0 |
|
|
|
||||||||||||||
0 0 0 |
|
|
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
0 0 0 |
|
0 0 1 |
|
0 0 0 |
|
0 0 0 |
|
|
|
0 |
|
|
|
4,5 |
0 |
|
|
0 |
0 |
|
|
6 |
|
|
|
0 |
|
|
− 4,5 |
0 |
|
|
0 |
|
0 |
|
|
3 |
|
|
|
|
||||||||||||||||||||
= |
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 −1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
0 0 0 |
|
0 0 0 |
|
|
0 0 0 |
|
−150 |
|
0 |
0 |
|
|
0 |
0 |
|
|
0 |
|
|
|
150 |
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
× |
|
|
||||||||||||||||||||||||
|
0 0 0 |
|
0 0 0 |
|
1 0 0 |
|
0 0 0 |
|
|
|
0 |
|
|
|
− 4,5 0 |
|
|
0 |
0 |
|
− 4,5 |
|
|
0 |
|
|
|
4,5 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4,5 |
|
|
||||||||||||||||||||||||||||||||||||||
0 0 0 |
|
0 0 0 |
|
0 0 1 |
|
0 0 0 |
|
|
|
0 |
|
|
|
0 |
− 4,5 |
|
0 |
4,5 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
4,5 |
|
|
0 |
|
4,5 |
|
|
0 |
|
|
|
|
||||||||||||||||||||
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 |
1 0 |
|
|
0 |
|
|
|
0 |
0 |
|
−1,5 |
0 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
1,5 |
0 |
|
|
0 |
|
|
|
|
|||||||||||||||||||||||
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
− 4,5 |
|
0 |
3 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
4,5 |
|
|
0 |
|
6 |
|
|
0 |
|
|
|
|
||||||
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
4,5 |
0 |
|
|
0 |
0 |
|
|
3 |
|
|
|
0 |
|
|
− 4,5 |
0 |
|
|
0 |
|
0 |
|
|
6 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 1 0 |
|
0 0 0 |
|
|
0 0 0 |
|
|
0 0 0 |
|
4,5 |
0 |
0 |
|
|
0 |
0 |
|
− 4,5 |
|
− 4,5 |
0 |
|
0 |
|
0 |
0 |
|
− 4,5 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 0 0 |
|
|
0 0 0 |
0 0 0 |
|
|
|
0 |
150 |
0 |
|
|
0 |
0 |
|
0 |
|
|
|
0 |
−150 |
0 |
|
0 |
0 |
|
|
0 |
|
|
||||||||||||||||||||||||
|
|
|
−1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 0 1 |
|
0 0 0 |
|
0 0 0 |
0 0 0 |
|
|
0 |
|
0 |
4,5 |
|
4,5 |
0 |
|
0 |
|
|
|
0 |
|
0 |
− 4,5 |
4,5 |
0 |
|
|
0 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4,5 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 0 0 |
|
0 1 0 |
|
0 0 0 |
0 0 0 |
|
0 |
|
0 |
4,5 |
|
|
6 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
3 |
0 |
|
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 0 0 |
|
−1 0 0 |
|
0 0 0 |
|
|
0 0 0 |
|
|
0 |
|
0 |
0 |
|
|
0 |
1,5 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
0 −1,5 |
|
0 |
. |
|||||||||||||||||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 1 |
|
0 0 0 |
0 0 0 |
|
|
|
|
|
|
0 |
0 |
|
|
0 |
0 |
|
6 |
|
|
|
4,5 |
|
0 |
|
0 |
|
0 |
0 |
|
|
3 |
|
|
||||||||||||||||||||||||
|
× |
|
|
|
= |
− 4,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 0 |
|
|
0 1 0 |
0 0 0 |
|
|
− 4,5 |
0 |
0 |
|
|
0 |
0 |
|
4,5 |
|
|
4,5 |
|
0 |
|
0 |
|
0 |
0 |
|
4,5 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 0 |
|
−1 0 0 |
0 0 0 |
|
|
|
0 |
−150 |
0 |
|
|
0 |
0 |
|
0 |
|
|
|
0 |
150 |
0 |
|
0 |
0 |
|
|
0 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 1 |
0 0 0 |
|
|
0 |
|
0 |
− 4,5 |
− 4,5 |
0 |
|
0 |
|
|
|
0 |
|
0 |
4,5 |
− 4,5 |
0 |
|
|
0 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 0 |
|
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 1 0 |
|
|
|
|
0 |
|
0 |
4,5 |
|
|
3 |
0 |
|
0 |
|
|
|
0 |
|
0 |
− 4,5 |
|
6 |
0 |
|
|
0 |
|
|
||||||||||||||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 0 |
|
0 0 0 |
−1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 −1,5 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
0 |
1,5 |
|
0 |
|
|
|||||||||||||||||
|
|
|
|
0 0 0 |
|
0 0 0 |
|
|
0 0 0 |
|
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
0 |
|
3 |
|
|
|
4,5 |
|
0 |
|
0 |
|
0 |
0 |
|
|
6 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. МСЕ в формі методу переміщень |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
3−4 |
= ТТ |
k′ |
|
|
Т |
3−4 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−4 |
|
|
3−4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
− 0,6 |
0 − 0,8 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
0 −1 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||
|
|
− 0,8 |
0 |
0,6 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
0 |
|
0 |
|
|
− 0,6 |
|
0 |
− 0,8 |
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 −1 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
− 0,8 0 |
0,6 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
− 0,6 |
|
0 |
− 0,8 |
|
|
0 |
0 |
0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 −1 |
0 |
|
|
0 |
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
− 0,8 0 |
0,6 |
|
|
0 |
0 |
0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
− 0,6 |
0 |
− 0,8 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 − 1 |
|
|
|
|
||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
0 |
|
||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
− 0,8 |
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
||||||||||||||||||||||
|
60 |
|
0 |
|
0 |
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
− 60 |
|
|
0 |
|
0 |
|
0 |
0 |
|
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
0 |
0,288 |
|
0 |
|
|
|
0 |
|
|
0 |
0,72 |
|
|
|
|
0 |
|
− 0,288 |
|
0 |
|
0 |
0 |
0,72 |
|
|||||||||||||||
|
|
0 |
|
0 |
0,288 |
|
|
|
0 − 0,72 |
|
0 |
|
|
|
|
0 |
|
|
0 |
− 0,288 |
|
0 |
− 0,72 |
|
|
0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
0,6 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
0 |
|
0 |
|
− 0,6 |
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||
|
0 |
|
0 − 0,72 |
|
0 |
2,4 |
|
0 |
|
|
|
|
0 |
|
|
0 |
0,72 |
|
0 |
1,2 |
|
|
0 |
|
||||||||||||||||||
|
|
0 |
0,72 |
|
0 |
|
|
|
0 |
|
|
0 |
2,4 |
|
|
|
|
0 − 0,72 |
|
0 |
|
0 |
0 |
1,2 |
|
|||||||||||||||||
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
||||
|
− 60 |
|
0 |
|
0 |
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
60 |
|
|
0 |
|
0 |
|
0 |
0 |
|
|
0 |
||||||||||||
|
|
0 |
− 0,288 |
|
0 |
|
|
|
0 |
|
|
0 |
− 0,72 |
|
|
0 |
|
|
0,288 |
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 0,72 |
|
|||||||||||||||||||||||||||
|
|
0 |
|
0 |
− 0,288 |
|
0 |
0,72 |
|
0 |
|
|
|
|
0 |
|
|
0 |
0,288 |
|
0 |
0,72 |
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
0 |
|
0 |
|
|
− 0,6 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
0 |
|
0 |
|
0,6 |
0 |
|
|
0 |
|
||||||||||
|
|
0 |
|
0 − 0,72 |
|
0 |
1,2 |
|
0 |
|
|
|
|
0 |
|
|
0 |
0,72 |
|
0 |
2,4 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||||
|
0 |
0,72 |
|
0 |
|
|
|
0 |
|
|
0 |
1,2 |
|
|
|
|
0 − 0,72 |
|
0 |
|
0 |
0 |
2,4 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
− 0,6 |
0 − 0,8 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 −1 |
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
||||||||||||||
|
|
− 0,8 0 |
0,6 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
0 |
|
0 |
|
|
− 0,6 |
0 |
− 0,8 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 −1 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
− 0,8 0 |
0,6 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||||||||
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
− 0,6 |
|
0 |
− 0,8 |
|
|
0 |
0 |
0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 −1 |
0 |
|
|
0 |
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
− 0,8 0 |
0,6 |
|
|
0 |
0 |
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
− 0,6 |
0 |
− 0,8 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 −1 |
|
|
|
|||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
0 |
|
||||||||||||||
|
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
− 0,8 |
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|||||||||||||||||||||||||
|
21,78 |
|
0 |
|
28,66 |
|
|
|
0 |
− 0,576 |
|
|
0 |
|
|
− 21,78 |
|
|
0 |
− 28,66 |
|
|
0 |
− 0,576 |
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
0 |
|
0,288 |
|
0 |
0,576 |
|
0 |
|
− 0,432 |
|
|
|
|
|
|
|
0 |
− 0,288 |
0 |
|
|
0,576 |
0 |
− 0,432 |
|
||||||||||||||||
|
28,66 |
|
0 |
|
38,50 |
|
|
|
0 |
0,432 |
|
|
0 |
|
|
− 28,66 |
|
|
0 |
− 38,50 |
|
|
0 |
0,432 |
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
0,576 |
|
0 |
1,752 |
|
0 |
|
− 0,864 |
|
|
|
|
|
|
|
0 |
− 0,576 |
0 |
|
|
0,552 |
0 |
− 0,864 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 0,432 |
|
|
|
|
|
|
|
|
|
|||
− 0,576 |
|
0 |
0,432 |
|
|
|
0 |
|
2,4 |
|
|
0 |
|
|
|
|
|
0,576 |
|
|
0 |
|
|
0 |
1,2 |
|
|
0 . |
||||||||||||||
|
0 |
− 0,432 |
|
0 |
− 0,864 |
|
0 |
|
|
1,24 |
|
|
|
|
|
|
|
0 |
|
|
0,432 |
0 |
|
− 0,864 |
0 |
|
|
|
|
|||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,048 |
|
||||||||||||||||||||||||||
|
− 21,78 |
|
0 |
− 28,66 |
|
|
|
0 |
0,576 |
|
|
0 |
|
|
|
|
|
21,78 |
|
|
0 |
28,66 |
|
|
0 |
0,576 |
|
|
0 |
|
|
|
|
|||||||||
0 |
− 0,288 |
|
0 |
− 0,576 |
|
0 |
|
|
0,432 |
|
|
|
|
|
|
|
0 |
|
|
0,288 |
0 |
|
− 0,576 |
0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,432 |
|
||||||||||||||||||||||||||
− 28,66 |
|
0 |
− 38,50 |
|
|
|
0 |
− 0,432 |
|
|
0 |
|
|
|
|
|
28,66 |
|
|
0 |
38,50 |
|
|
0 |
− 0,432 |
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
0,576 |
|
0 |
0,552 |
|
0 |
|
− 0,864 |
|
|
|
|
|
|
|
0 |
− 0,576 |
0 |
|
|
1,752 |
0 |
− 0,864 |
|
|||||||||||||||||
− 0,576 |
|
0 |
0,432 |
|
|
|
0 |
|
1,2 |
|
|
0 |
|
|
|
|
|
0,576 |
|
|
0 |
− 0,432 |
|
|
0 |
2,4 |
|
|
0 |
|
||||||||||||
|
0 |
− 0,432 |
|
0 |
− 0,864 |
|
0 |
|
|
0,048 |
|
|
|
|
|
|
|
0 |
|
|
0,432 |
0 |
|
− 0,864 |
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,24 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Елементи з матриці з жорсткості з скінченно-елементної з моделі з визначаються з як з реакції з уявних
в’язей по напрямах можливих переміщень вузлів шляхом сумировання кінцевих реакцій деформо-
6. МСЕ в формі методу переміщень |
71 |
ваних стержнів при одиничних вузлових переміщеннях. Ці реакції є компонентами матриць жорс-
ткості окремих скінченних елементів у глобальній системі координат.
K1,1 = k71−,72 + k12,1−3 = 100 + 4,5 = 104,5;
K2,1 = k81,−72 + k22,−1 3 = 0 + 0 = 0;
K3,1 = k91,−72 + k32,1−3 = 0 + 0 = 0;
K4,1 = k101−,27 + k42,−1 3 = 0 + 0 = 0;
K5,1 = k111−,72 + k52,1−3 = 0 + 0 = 0;
K6,1 = k121−,27 + k62,−1 3 = 0 – 4,5 = – 4,5;
K7,1 = k72,−1 3 = – 4,5;
K8,1 = k82,1−3 = 0;
K9,1 = k92,1−3 = 0;
K10,1 = k102−,13 = 0;
K11,1 = k112−,13 = 0;
K12,1 = k122−,13 = – 4,5.
K1,2 = k71−,82 + k12,2−3 = 0 + 0 = 0
K2,2 = k81,−82 + k22,−23 = 1,333 + 150 = 151,333;
K3,2 = k91,−82 + k32,−23 = 0 + 0 = 0;
K4,2 = k101−,28 + k42,−23 = 0 + 0 = 0;
K5,2 = k111−,28 + k52,−23 = 0 + 0 = 0;
K6,2 = k121−,28 + k62,−23 = – 2 + 0 = – 2;
K7,2 = k72,−23 = 0;
K8,2 = k82,−23 = – 150;
K9,2 = k92,−23 = 0;
K10,2 = k102−,23 = 0;
K11,2 = k112−,23 = 0;
K12,2 = k122−,23 = 0.
K1,3 = k71−,92 + k12,3−3 = 0 + 0 = 0;
K2,3 = k81,−92 + k22,−33 = 0 + 0 = 0;
6. МСЕ в формі методу переміщень |
72 |
||||||
K3,3 |
= k91,−92 + k32,−3 |
3 = 1,333 + 4,5 = 5,833; |
|
||||
K |
4,3 |
= k1−2 |
+ k 2−3 |
= 0 + 4,5 = 4,5; |
|
||
|
10,9 |
4,3 |
|
|
|||
K |
5,3 |
= k1− 2 |
+ k 2−3 |
= 2 + 0 = 2; |
|
||
|
11,9 |
5,3 |
|
|
|
||
K |
6,3 |
= k1−2 |
+ k 2−3 |
= 0 + 0 = 0; |
|
||
|
12,9 |
6,3 |
|
|
|||
K7,3 |
= k72,−33 = 0; |
|
|
|
|||
K8,3 |
= k82,−3 |
3 = 0; |
|
|
|
||
K9,3 = k92,−3 |
3 = – 4,5; |
|
|||||
K10,3 = k102−,33 = 4,5;
K11,3 = k112−,33 = 0;
K12,3 = k122−,33 = 0.
K |
|
= k1−2 + k 2−3 = 0 + 0 = 0; |
|||||
1,4 |
7,10 |
1,4 |
|
|
|||
K2,4 |
= k81,10−2 |
+ k22,−43 |
= 0 + 0 = 0; |
||||
K3,4 |
= k91,−102 + k32,−4 |
3 = 0 + 4,5 = 4,5; |
|||||
K |
4,4 |
= k1− 2 |
+ k |
2−3 |
= 1 + 6 = 7; |
||
|
10,10 |
|
4,4 |
|
|||
K |
5,4 |
= k1−2 |
+ k |
2−3 |
= 0 + 0 = 0; |
||
|
11,10 |
5,4 |
|
||||
K |
6,4 |
= k1−2 |
+ k |
2−3 |
= 0 + 0 = 0; |
||
|
12,10 |
6,4 |
|
||||
K7,4 |
= k72,−43 = 0; |
|
|
||||
K8,4 |
= k82,−4 |
3 = 0; |
|
|
|||
K9,4 |
= k92,−43 = – 4,5; |
||||||
K10,4 = k102−,43 = 3;
K11,4 = k112−,43 = 0;
K12,4 = k122−,43 = 0.
K1,5 = k71−,112 + k12,5−3 = 0 + 0 = 0;
K2,5 = k81,−112 + k22,−53 = 0 + 0 = 0;
K3,5 = k91,−112 + k32,−53 = 2 + 0 = 2;
K4,5 = k101−,211 + k42,−53 = 0 + 0 = 0;
K5,5 = k111−,112 + k52,−53 = 4 + 1,5 = 5,5;
6. МСЕ в формі методу переміщень |
73 |
|||||
K |
6,5 |
= k1−2 |
+ k 2−3 |
= 0 + 0 = 0; |
|
|
|
12,11 |
6,5 |
|
|
||
K7,5 |
= k72,−53 |
= 0; |
|
|
||
K |
8,5 |
= k 2−3 |
= 0; |
|
|
|
|
8,5 |
|
|
|
|
|
K9,5 |
= k92,−5 |
3 |
= 0; |
|
|
|
K10,5 = k102−,53 = 0;
K11,5 = k112−,53 = – 1,5
K12,5 = k122−,53 = 0.
K1,6 = k71−,122 + k12,6−3 = 0 – 4,5 = – 4,5;
K2,6 = k81,−122 + k22,−63 = – 2 + 0 = – 2;
K3,6 = k91,−122 + k32,−63 = 0 + 0 = 0;
K4,6 = k101−,122 + k42,−63 = 0 + 0 = 0;
K5,6 = k111−,122 + k52,−63 = 0 + 0 = 0;
K6,6 = k121−,122 + k62,−63 = 4 + 6 = 10;
K7,6 = k72,−63 = 4,5;
K8,6 = k82,−63 = 0;
K9,6 = k92,−63 = 0;
K10,6 = k102−,63 = 0;
K11,6 = k112−,63 = 0;
K12,6 = k122−,63 = 3.
K1,7 = k12,7−3 = – 4,5;
K2,7 = k22,−73 = 0;
K3,7 = k32,−73 = 0;
K4,7 = k42,−73 = 0;
K5,7 = k52,−73 = 0;
K6,7 = k62,−73 = 4,5;
K7,7 = k72,−73 + k13,1−4 = 4,5 + 21,784 = 26,284;
K8,7 = k82,−73 + k23,−14 = 0 + 0 = 0;
6. МСЕ в формі методу переміщень |
74 |
|||||||
K9,7 |
= k92,−73 + k33,−1 |
4 |
= 0 + 28,662 = 28,662; |
|
||||
K = k 2−3 |
+ k 3−4 |
= 0 + 0 = 0; |
|
|||||
10,7 |
10,7 |
4,1 |
|
|
||||
K |
|
= k 2−3 |
+ k 3−4 |
= 0 – 0,576 = – 0,576; |
|
|||
11,7 |
11,7 |
5,1 |
|
|
||||
K |
|
= k 2−3 |
+ k 3−4 |
= 4,5 + 0 = 4,5. |
|
|||
12,7 |
12,7 |
6,1 |
|
|
||||
K |
|
= k 2−3 = 0; |
|
|
|
|||
1,8 |
1,8 |
|
|
|
|
|
|
|
K2,8 |
= k22,−83 |
= – 150; |
|
|||||
K3,8 |
= k32,−8 |
3 |
|
= 0; |
|
|
|
|
K4,8 |
= k42,−83 |
= 0; |
|
|
|
|||
K5,8 |
= k52,−8 |
3 |
|
= 0; |
|
|
|
|
K6,8 |
= k62,−8 |
3 |
= 0; |
|
|
|
||
K |
7,8 |
= k 2−3 |
|
+ k 3−4 |
= 0 + 0 = 0; |
|
||
|
7,8 |
|
1,2 |
|
|
|
||
K8,8 |
= k82,−8 |
3 |
+ k23,−24 |
= 150 + 0,288 = 150,288; |
|
|||
K9,8 |
= k92,−8 |
3 |
+ k33,−24 |
= 0 + 0 = 0; |
|
|||
K |
|
= k 2−3 |
+ k 3−4 |
= 0 + 0,576 = 0,576; |
|
|||
10,8 |
10,8 |
4,2 |
|
|
||||
K = k 2−3 |
+ k 3−4 |
= 0 + 0 = 0; |
|
|||||
11,8 |
11,8 |
|
5,2 |
|
|
|||
K |
|
= k 2−3 |
+ k 3−4 |
= 0 – 0,432 = – 0,432. |
|
|||
12,8 |
12,8 |
6,2 |
|
|
||||
K |
|
= k 2−3 = 0; |
|
|
|
|||
1,9 |
1,9 |
|
|
|
|
|
|
|
K2,9 |
= k22,−93 |
= 0; |
|
|
|
|||
K3,9 |
= k32,−9 |
3 |
|
= – 4,5 |
|
|||
K4,9 |
= k42,−93 |
= – 4,5; |
|
|||||
K5,9 |
= k52,−9 |
3 |
= 0; |
|
|
|
||
K6,9 |
= k62,−9 |
3 |
= 0; |
|
|
|
||
K |
7,9 |
= k 2−3 |
|
+ k 3−4 |
= 0 + 28,662 = 28,662; |
|
||
|
7,9 |
|
1,3 |
|
|
|
||
K8,9 |
= k82,−9 |
3 |
+ k23,−34 |
= 0 + 0 = 0; |
|
|||
K9,9 |
= k92,−93 |
+ k33,−34 |
= 4,5 + 38,504 = 43,004; |
|
||||
K |
|
= k 2−3 |
+ k 3− 4 |
= – 4,5 + 0 = – 4,5; |
|
|||
10,9 |
10,9 |
4,3 |
|
|
||||
K |
|
= k 2−3 |
+ k 3−4 |
= 0 + 0,432 = 0,432; |
|
|||
11,9 |
11,9 |
5,3 |
|
|
||||
6. МСЕ в формі методу переміщень |
75 |
|||||||
K = k |
2−3 |
+ k 3− 4 |
= 0 + 0 = 0. |
|
||||
12,9 |
12,9 |
|
6,3 |
|
|
|||
K |
|
= k |
2−3 |
= 0; |
|
|
||
1,10 |
1,10 |
|
|
|
|
|
||
K2,10 |
= k22,−103 = 0; |
|
|
|||||
K3,10 |
= k32,10−3 |
= 4,5 |
|
|
||||
K4,10 |
= k42,−103 = 3; |
|
|
|||||
K5,10 |
= k52,10−3 |
= 0; |
|
|
||||
K6,10 |
= k62,10−3 = 0; |
|
|
|||||
K |
7,10 |
= k |
2−3 |
+ k 3−4 |
= 0 + 0 = 0; |
|
||
|
|
7,10 |
|
1,4 |
|
|
||
K |
8,10 |
= k |
2−3 |
+ k 3−4 |
= 0 + 0,576 = 0,576; |
|
||
|
|
8,10 |
|
2,4 |
|
|
||
K9,10 |
= k92,10−3 + k33,−44 |
= – 4,5 + 0 = – 4,5; |
|
|||||
K |
|
= k 2−3 |
+ k 3−4 = 6 + 1,752 = 7,752; |
|
||||
10,10 |
|
10,10 |
|
4,4 |
|
|
||
K |
|
= k 2−3 |
|
+ k |
3− 4 = 0 + 0 = 0; |
|
||
11,10 |
|
11,10 |
5,4 |
|
|
|||
K |
|
= k 2−3 |
+ k 3−4 = 0 – 0,864 = – 0,864. |
|
||||
12,10 |
|
12,10 |
|
6,4 |
|
|
||
K |
|
= k 2−3 = 0; |
|
|
||||
1,11 |
1,11 |
|
|
|
|
|
||
K2,11 = k22,−113 |
= 0; |
|
|
|||||
K3,11 = k32,11−3 |
= 0; |
|
|
|||||
K4,11 = k42,−113 |
= 0; |
|
|
|||||
K5,11 = k52,11−3 |
= – 1,5; |
|
||||||
K6,11 = k62,−113 |
= 0; |
|
|
|||||
K |
7,11 |
= k |
2−3 |
+ k 3−4 |
= 0 – 0,576 = – 0,57;6 |
|
||
|
|
7,11 |
|
1,5 |
|
|
||
K8,11 = k82,11−3 + k23,−54 |
= 0 + 0 = 0; |
|
||||||
K9,11 = k92,11−3 + k33,−54 |
= 0 + 0,432 = 0,432; |
|
||||||
K |
|
= k 2−3 |
|
+ k |
3− 4 = 0 + 0 = 0; |
|
||
10,11 |
|
10,11 |
|
4,5 |
|
|
||
K |
|
= k 2−3 |
|
+ k |
3−4 = 1,5 + 2,4 = 3,9; |
|
||
11,11 |
|
11,11 |
5,5 |
|
|
|||
K |
|
= k 2−3 |
|
+ k |
3− 4 = 0 + 0 = 0. |
|
||
12,11 |
|
12,11 |
|
6,5 |
|
|
||
K |
|
= k |
2−3 |
= – 4,5; |
|
|||
1,12 |
1,12 |
|
|
|
|
|
||
K2,12 |
= k22,−123 = 0; |
|
|
|||||

|
|
Е в |
ормі мето |
перемі ен |
76 |
|||
K3,12 |
k3,122 3 |
0; |
|
|
|
|
|
|
K4,12 |
k4,122 3 |
0; |
|
|
|
|
|
|
K5,12 |
k5,122 3 |
0; |
|
|
|
|
|
|
K6,12 |
k6,122 3 |
3; |
|
|
|
|
|
|
K |
7,12 |
k 2 3 |
k3 |
4 |
|
4,5 + 0 = 4,5; |
|
|
|
7,12 |
1,6 |
|
|
|
|
|
|
K |
8,12 |
k2 3 |
k3 |
4 |
|
0 – 0,432 = – 0,432; |
|
|
|
8,12 |
2,6 |
|
|
|
|
||
K9,12 |
k9,122 3 |
k3,63 |
4 |
|
0 + 0 = 0; |
|
|
|
K |
|
k 2 3 |
k3 |
4 |
0 – 0,864 = – 0,864; |
|
||
10,12 |
10,12 |
4,6 |
|
|
|
|||
K |
|
k 2 3 |
k3 4 |
0 + 0 = 0; |
|
|
||
11,12 |
11,12 |
5,6 |
|
|
|
|
||
K |
|
k 2 3 |
k3 |
4 |
6 + 1,248 = 7,248. |
|
||
12,12 |
12,12 |
6,6 |
|
|
|
|
||
исте а лінійни рівн н
К0
при по удовани атриці жорсткості К та векторі ву лови навантажен |
ає ро в ок |
1
2
3
4
5
6
7
8
9
10
11
12
0,0293
15,416
7,1195
0,5817 3,6154 6,3429 . 10,320 15, 468 7,6655 0,5384 3,7638 4,6578
усилл |
в крайні |
точка |
стержневи |
скінченни |
еле |
ентів ви начают с |
а фор улою |
|||||||||||
|
|
N |
i |
i |
i |
i |
i |
i |
|
N |
j |
j |
j |
j |
j |
j |
ki j |
|
|
|
|||||||||||||||||
|
Si j |
|
Qz |
Qy M |
р M y |
Mz |
|
|
Qz |
Qy |
M р |
M y |
Mz |
Ti j δi j , |
||||
де δi j – вектор ву лови |
пере |
і ен скінченно о еле |
ента в |
ло ал ній систе і координат, ко |
||||||||||||||
поненти |
ко о є під |
ножиною |
атриці |
: |
|
|
|
|
|
|
|
|
|
|
||||
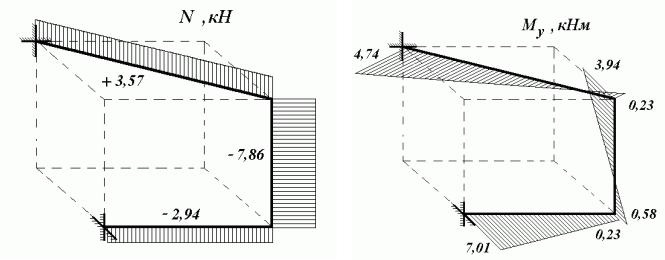
6. МСЕ в формі методу переміщень |
|
|
|
|
|
|
|
77 |
|||||
|
|
0 |
|
|
|
− 0,0293 |
|
|
10,320 |
|
|||
|
|
0 |
|
|
|
|
− 15,416 |
|
|
|
|
− 15,468 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
− 7,1195 |
|
|
|
− 7,6655 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
− 0,5817 |
|
|
|
|
0,5384 |
|
|
|
|
0 |
|
|
|
|
3,6154 |
|
|
|
|
3,7638 |
|
|
|
0 |
|
, |
|
|
|
|
, |
|
|
|
|
|
|
|
|
− 6,3429 |
|
− 4,6578 . |
|||||||
δ1−2 |
= |
|
|
|
δ2−3 |
= |
|
|
|
δ3−4 |
= |
|
|
− 0,0293 |
|
|
|
|
|||||||||
|
10,320 |
|
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− 15,416 |
|
|
|
|
− 15,468 |
|
|
|
|
0 |
|
|
|
− 7,1195 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 7,6655 |
|
|
|
0 |
|
|||
|
− 0,5817 |
|
|
|
0,5384 |
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,6154 |
|
|
|
3,7638 |
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
− 6,3429 |
|
|
− 4,6578 |
|
|
|
|
|||||
Враховуючи ці вектори отримуємо
|
|
− N |
|
|
|
2,93 |
|
|
|
|
Qy |
|
|
|
7,87 |
|
|
|
|
|
|
|
|
|
||
|
|
Qz |
|
|
|
2,26 |
|
|
|
|
M кр |
|
|
|
|
|
|
|
|
|
|
0,58 |
|
|
||
|
|
M y |
|
|
|
|
|
|
|
|
|
|
− 7,01 |
, |
|||
|
|
− M z |
|
|
18,14 |
|
||
S1−2 |
= |
|
|
|
= |
|
|
|
|
|
|
|
|||||
|
|
N |
|
|
− 2,93 |
|
||
|
|
− Q |
|
|
− 7,87 |
|
||
|
|
|
y |
|
|
|
|
|
|
|
− Qz |
|
− 2,26 |
|
|||
|
− M |
|
|
− 0,58 |
|
|||
|
|
− M |
кр |
|
|
|
|
|
|
|
|
|
|
0,23 |
|
|
|
|
|
|
у |
|
5,46 |
|
|
|
|
|
M z |
|
|
|
|
||
|
|
− N |
|
|
|
7,86 |
|
||
|
|
Qy |
|
|
|
|
|
|
|
|
|
|
|
− 2,93 |
|
||||
|
|
Q |
|
|
|
|
2,26 |
|
|
|
|
|
z |
|
|
|
|
|
|
|
M кр |
|
− 0,23 |
|
|||||
|
|
M |
|
|
|
− 0,58 |
|
||
|
|
|
y |
|
|
|
|
|
, |
|
|
− M z |
|
− 5,46 |
|||||
S2−3 |
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
|
|
N |
|
|
|
− 7,86 |
|
||
|
|
− Qy |
|
|
2,93 |
|
|
||
|
|
|
|
|
|
||||
|
|
− Qz |
|
− 2,26 |
|
||||
|
|
|
|
|
|
|
0,23 |
|
|
|
− M кр |
|
|
|
|||||
|
|
− M |
|
|
|
− 3,94 |
|
||
|
|
M z |
y |
|
|
|
|
||
|
|
|
|
− 0,40 |
|
||||
|
|
− N |
|
|
− 3,57 |
|
||
|
|
Qy |
|
|
|
2,13 |
|
|
|
|
|
|
|
|
|||
|
|
Q |
z |
|
|
− 0,99 |
||
|
|
|
|
|
|
|
|
|
|
M кр |
|
||||||
|
|
|
|
2,04 |
|
|||
|
|
M |
|
|
|
|
0,23 |
|
|
|
|
y |
|
|
|
|
|
|
|
− M z |
|
3,40 |
. |
|||
S3−4 |
= |
|
|
|
|
= |
|
|
|
|
|
3,57 |
|||||
|
|
N |
|
|
|
|
|
|
|
|
− Q |
|
|
|
− 2,13 |
||
|
|
|
|
y |
|
|
|
|
|
|
− Qz |
|
0,99 |
|
|||
|
− M |
|
|
− 2,04 |
||||
|
|
− M |
кр |
|
|
|
||
|
|
|
|
4,74 |
|
|||
|
|
|
|
y |
|
|
|
|
|
|
M z |
|
7,27 |
|
|||
По отриманих значеннях внутрішніх зусиль будуються епюри (рис.6.40).
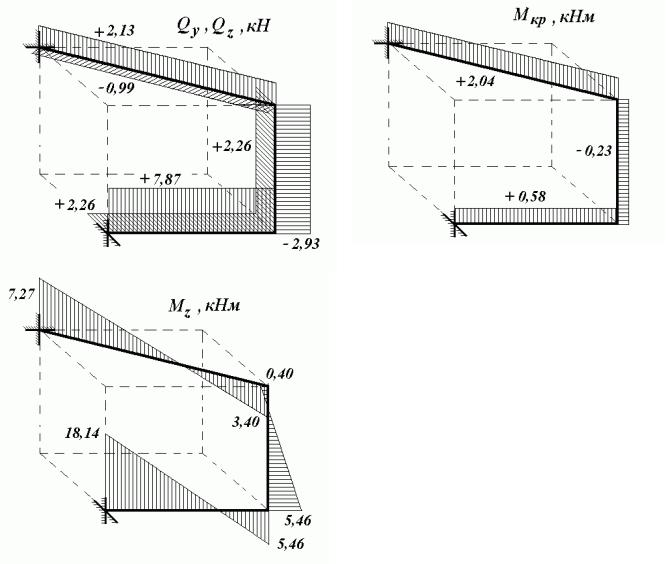
6. МСЕ в формі методу переміщень |
78 |
Рис.6.40
ДО ЗМІСТУ ПІДРУЧНИКА
7. Розрахунок стержневих систем методом скінченних
елементів у формі методу сил
Зміст глави
7.1. Кінцеві зусилля в скінченних елементах
7.2. Матриця податливості скінченного елемента
7.3. Вузлові характеристики скінченно-елементноїи моделі
7.4. Матриця податливостіи і матрицяи жорсткостіи скінченно-елементноїи моделі
7.5. Рівняння рівноваги вузлів скінченно-елементноїи моделі
7.6. Повна система рівнянь та її розв’язок
7.7.Обчислення дійсних зусиль у стержнях
7.1. Кінцеві зусилля в скінченних елементах
Розглянемо на площині стержневий скінченний елемент, що на кінцях жорстко приєднується до вузлів (рис.7.1,а). Як і раніше, вважатимемо його елементом першого типу.
Рис.7.1

7. МСЕ в формі методу сил |
2 |
Вектор кінцевих зусиль для такого стержня має шість компонентів:
(s )T = {M |
Q N |
i |
M |
j |
Q |
j |
N |
} . |
k e |
i i |
|
|
j |
|
Додатні напрями для кінцевих зусиль наведено на рис.7.1,б.
Як изазначалось иу ип.4.2, идля искінченно-елементної истержневої имоделі, иколи инавантаження ина исте-
ржень відсутні, з умов рівноваги випливає:
Ni = N j = N ,
Qi = Q j = Q = (M j − M i ) l ,
l ,
тобто всі компоненти вектори кінцевих зусиль можуть бути виражені через три параметри Mi, Mj i
N: |
|
|
|
|
|
|
|
|
(sk )e |
= L e se , |
|
(7.1) |
|
де |
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
− 1 l |
1 l |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
L e = |
|
|
, |
(7.2) |
|
|
|
0 |
0 |
1 |
|
|
|
− 1 l |
1 l |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
seT = {Mi M j |
N} |
– вектор зусиль. |
|
|
|
|
|
|
e |
|
|
|
|
Оскільки в межах скінченного елементу не діють розподілені навантаження, згинальні моменти є лінійною функцією:
M ( x ) = α1 + α 2 x .
Постійні α1,α2 визначаються із граничних умов: |
|
|
|
|
|
|
при x = 0 |
M ( 0 ) = α1 = M i ; |
|
|
|
|
|
при x = l |
M ( l ) = α1 + α 2 l = M j . |
|
|
|
|
|
Розв’язавши ці рівняння, дістанемо: |
|
|
|
|
|
|
|
α1 = M i , α 2 = − |
M |
i |
+ |
M j |
|
|
|
|
. |
|||
|
l |
|
|
|||
|
|
|
|
l |
||
Отже, внутрішні зусилля в будь-якому перерізі подаються залежностями:
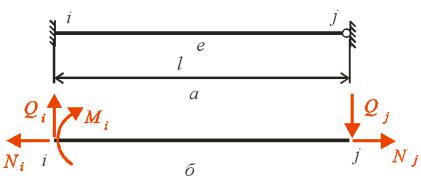
7. МСЕ в формі методу сил |
3 |
|
|
x |
x |
|
||
M ( x ) = 1 |
− |
|
M i + |
|
M j |
, |
|
|
|||||
|
|
l |
l |
(7.3) |
||
N( x ) = N . |
|
|
|
|
|
|
Поперечна сила в перерізі стержня може розглядатись як похідна від функції згинального мо-
менту:
|
|
|
|
|
|
|
Q( x ) = |
dM ( x ) |
= − |
1 |
M i + |
1 |
M j . |
(7.4) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
l |
|
|
l |
|
|
||||
Співвідношення (7.3) запишемо в матричній формі: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
M |
|
|
||||
|
|
|
|
|
|
|
M ( x ) |
1 |
− |
|
|
0 |
i |
|
|||||||||
|
|
|
|
|
|
|
l |
l |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
N( x ) |
|
= |
|
|
|
M j |
(7.5) |
||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
||
або |
|
|
|
|
|
|
|
(s |
(x))e = (H(x))(sk )e , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
(7.6) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x))e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де (s |
– вектор прогонових зусиль елемента, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
− |
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H(x) = 1 |
|
|
|
0 |
– матриця апроксимації прогонових зусиль. |
|
|||||||||||||||||
l |
|
l |
|
||||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вигляд матриці апроксимації і вектора прогонових зусиль елемента залежить від граничних умов. Так, для скінченного елементу другого типу (рис.7.2), який має жорсткий вузол на початку і шарнір на кінці:
Рис.7.2
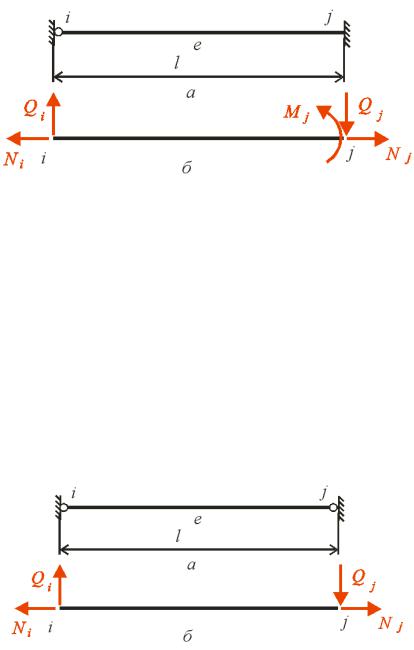
7. МСЕ в формі методу сил |
4 |
M ( x ) |
|
|
x |
|
|
|
= 1 |
− l |
|
N( x ) |
|
0 |
|
|
|
|
|
|
|
де
0 M
i , (7.7)
N
1
(s ) |
|
|
− |
x |
|
(7.8) |
= {M N}T , H(x) = 1 |
|
0 . |
||||
|
|
|
|
|
|
|
k e |
i |
|
0 |
l |
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
Для скінченного елементу третього типу, який має шарнір на початку і затиснення на кінці
(рис.7.3):
Рис.7.3
M ( x ) |
|
x |
0 |
M j |
|
|
|
|
||||||
= |
|
|
|
|
|
(7.9) |
||||||||
|
N( x ) |
|
|
|
N |
, |
|
|
|
|||||
|
|
|
l |
|
|
|
|
|
|
|
||||
|
|
0 |
1 |
|
|
|
|
|
||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sk )T = {M j |
|
N} , |
|
H(x) = |
x |
|
|
|||||||
|
|
|
|
0 . |
(7.10) |
|||||||||
|
|
l |
||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
І зрештою, для скінченного елементу четвертого типу (шарніри на початку і на кінці) (рис.7.4)
матриця апроксимації вироджується у число 1.
Рис.7.4

7. МСЕ в формі методу сил |
5 |
Вектор прогонових зусиль елемента містить тільки один елемент − поздовжню силу: |
|
(N(x))e = 1 × [N ]. |
(7.11) |
7.2. Матриця податливості скінченного елемента
Розглянемо потенціальну енергію деформацій стержня, в якому виникають поздовжні дефор-
мації :і деформації згину.
|
|
|
|
|
l |
|
|||
|
|
|
U = |
1 |
∫ [M ( x )κ( x ) + N( x )ε( x )]dx . |
(7.12) |
|||
|
|
|
|
||||||
|
|
|
2 |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
||
Кривизна κ( x ) = |
M ( x ) |
|
і поздовжні деформації ε( x ) = |
N( x ) |
|
можуть бути записані у ви- |
|||
EI |
EA |
||||||||
|
|
|
|
|
|||||
гляді:
κ( x ) |
1 |
0 |
|
|
|
||||
|
|
|
M ( x ) |
||||||
|
|||||||||
|
|
= EI |
1 |
|
|
|
|||
|
ε( x ) |
0 |
|
N( x ) |
|||||
|
|
||||||||
|
|
|
|
EA |
|
|
|||
або
де (ε( x))e
1 d e = EI
0
(ε( x))e = de (s ( x))e ,
= { κ(x) ε(x)}Te − вектор деформацій перерізу стержня,
0
− матриця податливості перерізу стержня,
1
EA e
(s |
(x))e = {M (x) N (x)}Te |
|
|
(7.13)
(7.14)
(7.15)
– вектор прогонових зусиль елемента
Використовуючи наведені позначення, потенціальну енергію деформації (7.12) запишемо в ма-
тричній формі:
U = 1 |
l |
|
(s |
( x))e dx . |
(7.16) |
|
∫(ε ( x))e |
||||||
|
|
|
T |
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Підставивши (7.14) і (7.15) у (7.16) і виконавши операцію транспонування, одержимо:
7. МСЕ в формі методу сил |
6 |
|
1 |
l |
|
|
|
U = |
|
∫ |
(σ(x))Te dTe |
(s(x))e dx . |
(7.17) |
2 |
|||||
|
|
||||
|
|
0 |
|
|
|
Прогонові зусилля можуть бути виражені за допомогою (7.6) через матрицю апроксимації сте-
ржня:
|
1 l |
|
|
|
|
|
|
|
1 |
l |
|
|
|
|
||
U = |
|
|
((H(x))(sk )e )T de |
(H(x)(sk )e )dx = |
|
|
(sk )Te |
(H(x))T d e |
(H(x))(sk )e dx . (7.18) |
|||||||
2 ∫ |
2 |
∫ |
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо вектори кінцевих зусиль(sk )e |
i |
(sk )Te |
винести за знак інтеграла, як такі, що не залежать |
|||||||||||||
від координати x, потенціальна енергія набере вигляду |
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
l |
|
|
|
|
|
|
|
|
||
|
|
|
U = |
|
|
(sk )T |
∫ |
(H(x))T |
d e (H(x))dx |
(sk ) |
(7.19) |
|||||
|
|
|
2 |
|||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
e |
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U = |
|
(sk )Te |
b e (sk )e , |
|
|
(7.20) |
||||
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де позначено: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
b e = ∫l |
(HT (x)) d e (H(x))dx . |
|
(7.21) |
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Отже, потенціальна енергія деформації стержня є квадратичною функцією кінцевих зусиль.
Величину be для елемента першого типу (рис.7.1) після перемноження матриць згідно з (7.21)
можна записати у вигляді:
|
|
|
|
|
1 |
|
|
|
x 2 |
|
1 |
|
|
x |
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 - |
|
|
|
|
|
|
× |
|
|
1 |
- |
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
EI |
|
l |
|
EI l |
|
l |
|
|
|
||||||||||||||||||
|
|
|
l |
|
1 |
|
|
|
x |
|
|
|
x |
|
|
|
1 x |
2 |
|
|
|
|
|
||||||||
b |
e |
= |
∫0 |
|
|
|
× |
|
|
1 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
dx . |
(7.22) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
EI |
|
|
|
l |
|
|
|
l |
|
|
EI l |
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
Таким чином, be – це квадратна матриця. Проінтегруємо її елементи:
7. МСЕ в формі методу сил |
7 |
|
|
|
l |
|
|
1 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l dx |
|
|
l |
|
||||||||||||||
b |
|
= |
|
|
|
|
|
|
1 |
- |
|
|
|
|
dx |
= |
|
|
|
|
|
, b |
|
|
= |
|
|
= |
|
|
, |
|||||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ EI |
EA |
|||||||||||||||||||||||||||||
11 |
|
|
EI |
|
|
l |
|
|
|
|
|
|
|
3EI |
|
|
33 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||||||||||
b |
|
= b |
|
|
|
= |
|
|
|
|
|
|
|
× |
|
|
1 |
- |
|
|
|
dx |
= |
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
∫ EI |
|
l |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
12 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x 2 |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
b |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
, b |
|
|
= b |
|
|
= b |
|
= b |
= 0. |
|||||||||||||
|
∫ EI |
|
|
|
|
|
3EI |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
22 |
|
l |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
23 |
31 |
|
32 |
|
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Після підстановки обчислених елементів матриця be |
набуває остаточного вигляду: |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3EI |
|
6EI |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
b e |
= |
|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
0 |
|
|
|
|
|
|
(7.23) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3EI |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA e |
|
|
|
|
|
|
|
||||||||
Матриця be – це матриця податливості стержня. Аналогічна матриця (4.30) була одержана в п.4.4 простішим шляхом: за допомогою інтеграла Мора. Спосіб одержання матриці податливості,
застосований в даному параграфі, є найбільш загальним і може бути використаний при розрахунку будь-яких плоских або просторових систем.
Матриця жорсткості скінченного елемента, який розглядається з позицій методу сил, може бу-
ти визначена як обернена до матриці податливості:
|
4EI |
- |
2EI |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
l |
l |
|
||||||||
|
|
|
|
|
|
|
|
||||
|
2EI |
|
4EI |
|
|
|
|
||||
k e = b e−1 = - |
|
0 |
. |
(7.24) |
|||||||
l |
|
|
l |
||||||||
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
0 |
|
|
EA |
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
l |
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
e |
|
|
Для скінченного елемента другого типу (рис.7.2) аналогічні матриці матимуть вигляд:
sT = {M |
i |
N} |
|
, |
(7.25) |
|
e |
|
|
e |
|
|
|
|
l |
|
0 |
|
|
|
|
|
|
|
|
||
3EI |
|
(7.26) |
||||
b e = |
|
l |
, |
|||
|
0 |
|
|
|
||
|
|
|
||||
|
|
|
EA e |
|
||
7. МСЕ в формі методу сил |
8 |
3EI |
0 |
|
|
||
|
|
|
|
||
l |
|
||||
k e = |
|
EA |
. |
(7.27) |
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|||
|
|
|
l |
e |
|
Скінченний елемент третього типу (рис.7.3) відрізняється від попереднього лише вектором зу-
силь, який має вигляд: |
|
|
|
seT = {M j |
N} |
. |
(7.28) |
|
|
e |
|
І зрештою, для елемента четвертого типу (рис.7.4) вектор зусиль, матриця податливості і мат-
риця жорсткості мають лише по одному елементу:
s |
= {N} , |
b |
|
= |
l |
|
, |
k |
|
= |
EA |
. |
(7.29) |
e |
|
|
e |
|
|||||||||
e |
e |
|
|
|
|
|
|
l |
|
|
|||
|
|
|
|
EA e |
|
|
|
|
e |
|
|||
7.3. Вузлові характеристики скінченно-елементної моделі
Головними ивузловими ихарактеристиками искінченно-елементної имоделі истержневої исистеми ипри розрахунку її за методом скінченних елементів у формі методу сил є вектор зусиль, який склада-
ється з векторів зусиль окремих стержнів:
ST = {s1 s2 … si … sm} ,
вектор и вузлових и переміщень и скінченно-елементної и моделі, и що и складається и з и векторів и вузлових и пе-
реміщень окремих вузлів:
T = { 1 |
2 … k … n}T , |
|||
а також вектор вузлових навантажень |
|
|
|
|
|
|
|
|
|
FT = {F1 F2 … Fk … Fn} .
Питання побудови векторів |
і F докладно розглянуто у п.6.7. |
Приклад 7.1. Побудувати вектори переміщень, вузлових навантажень і зусиль для рами
(рис.7.5,а).
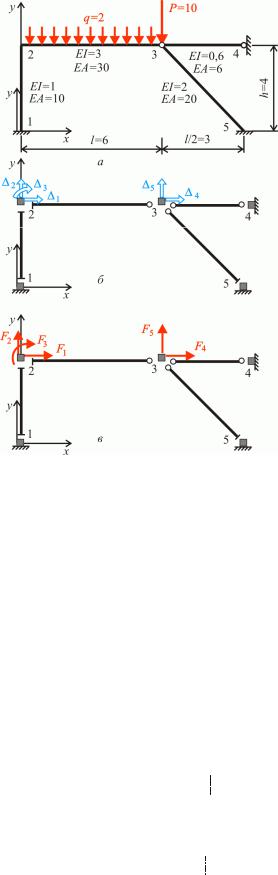
7. МСЕ в формі методу сил |
9 |
Рис.7.5
Передусім замінюємо раму дискретною моделлю (рис.7.5,б), тобто розглядаємо раму як сукуп-
ність окремих стержнів (скінченних елементів) і вузлів. Кількість ступнів вільності скінченноеле-
ментної моделі дорівнює п’яти. Справді, три ступні вільності має жорсткий вузол 2 (поступальні
переміщення |
1 і |
2 , а також кут повороту 3 ) і два ступня вільності має вузол 3 (поступальні |
переміщення |
4 і |
5 ). Отже, для вільних вузлів можемо записати |
T2 = {
T3 = {
а для всієї системи
1 2 3} ,
4 5} ,
T = { 2 |
3} = { 1 2 |
3 |
4 |
5} . |
Вектор вузлових навантажень матиме також п’ять складових:
|
|
} , |
FT = {F2 F3} = {F1 F2 F3 F4 F5 |
||
які обчислюються в такий самий спосіб, як і при розрахунку стержневих систем за методом скін-
ченних елементів у формі методу переміщень:
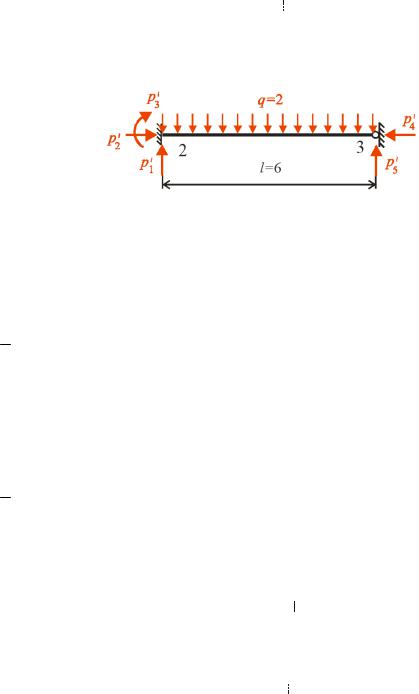
7. МСЕ в формі методу сил |
10 |
F = P + Q ,
де вектор P характеризує компоненти зовнішніх навантажень, які діють на вузли стержневої сис-
теми, а вектор Q містить компоненти вузлових реакцій, які передаються на вузли скінченноеле-
ментної моделі внаслідок розподілених вздовж стержня навантажень. У прикладі, що розглядаєть-
ся
PT = {0 0 0  0 −10} .
0 −10} .
Вантажні реакції на кінцях стержня 2-3 (рис.7.6) обчислюються за формулами, що наведені у
п.6.6.
Рис.7.6
Отже, маємо:
p′ = 0 ,
1
p¢2 = - 5 × (- 2)× 6 = 7,5,
8
p3¢ = (- 2)× 62 = -9 ,
8
p′ = 0 ,
4
p5¢ = - 3 (- 2)× 6 = 4,5 .
8
Означені и реакції ипередаються и на и вузли и скінченно-елементної и моделі иу и протилежних инапрямах. и То-
му можемо записати:
QT = {0 −7,5 9  0 −4,5} .
0 −4,5} .
Отже вектор вузлових навантажень всієї скінченно-елементної моделі:
FT = {0 −7,5 9  0 −14,5} .
0 −14,5} .
Склад невідомих зусиль у кожному стержні системи залежить від типу граничних умов. Так,
стержень 1-2 є стержнем першого типу (жорсткі вузли з обох боків), стержень 2-3 − другого типу
7. МСЕ в формі методу сил |
11 |
(жорсткий вузол на початку і шарнір на кінці), стержень 2-4, який має шарнір на початку і жорст-
кий вузол на кінці, може бути віднесений ло третього, а стержень 2-5 (шарніри з обох боків) − до четвертого типу. Звідси вектор зусиль скінченно-елементної моделі набере вигляду:
|
|
|
s2−4} = |
ST = { s1−2 |
s2−3 |
s2−5 |
|
= {M1−2 |
M 2−1 |
N1−2 |
M 2−3 N2−3 M5−3 N3−5 N3−4} . |
Величини зусиль, які входять до цього вектора, становлять основні невідомі задачі.
7.4. Матриця податливості і матриця жорсткості скінченно-елементної моделі
Матриця податливості і матриця жорсткості скінченно-елементної моделі є квадратними матри-
цями, кількість рядків і стовпців в яких дорівнює кількості основних невідомих задачі, тобто кіль-
кості елементів вектора зусиль S .
Матриця податливості має блочно-діагональну структуру: блоки, що розташовані на головній діагоналі, становлять матриці податливості окремих скінченних елементів, а всі інші блоки є ну-
льовими:
b1 |
0 |
0 |
|
|
0 |
b 2 |
0 |
|
(7.30) |
B = |
|
|
. |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
b m |
|
||
Аналогічно може бути побудована матриця жорсткості скінченно-елементної моделі:
k1 |
0 |
0 |
|
|
0 |
k 2 |
0 |
|
(7.31) |
K = |
|
|
. |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
k m |
|
||
У співвідношенні (7.31) блоки k i являють собою матриці жорсткості окремих скінченних елемен-
тів, вигляд яких залежить від їхнього типу.
Як і завжди, між матрицями податливості і жорсткості виконується залежність |
|
K = B −1 , |
(7.32) |
тобто матриця жорсткості є оберненою щодо до матриці податливості.

7. МСЕ в формі методу сил |
12 |
Приклад 7.2. Скласти матриці податливості і жорсткості для стержневої схеми (див.рис.7.5,а).
Насамперед обчислимо елементи матриць для кожного стержня залежно від типу граничних
умов.
∙ Стержень 1-2 (перший тип):
|
1,3333 |
0,6667 |
0 |
|
|
|
|
|
1 |
− 0,5 |
0 |
|
|
|
b |
= 0,6667 |
1,3333 |
0 |
|
, |
k |
1−2 |
= − 0,5 |
1 |
0 |
|
; |
||
1−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0,4 |
|
|
|
|
0 |
0 |
2,5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ Стержень 2-3 (другий тип): |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b2−3 |
0,6667 |
0 |
k 2−3 |
1,5 |
0 |
|
|
= |
0 |
, |
= |
; |
||
|
|
|
0,2 |
|
0 |
5 |
|
∙ |
Стержень 3-5 (третій тип): |
|
|
|
|
||
|
b3−5 |
0,8333 |
0 |
k3−5 |
1,2 |
0 |
|
|
= |
0 |
, |
= |
; |
||
|
|
|
0,25 |
|
0 |
4 |
|
∙ |
Стержень 3-4 (четвертий тип): |
|
|
|
|
||
|
b3−4 = [0,5], |
|
k3−4 = [2,0]. |
|
|||
Тоді матриця податливості всієї скінченно-елементної моделі (рис.7.5,б) набуде вигляду:
|
|
b1−2 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = 0 |
|
b2−3 |
0 |
0 |
|
= |
|
|
|
|
|
0 |
|
0 |
b3−5 |
0 |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|
b3−4 |
|
|
|
|
|||
1,3333 |
0,6667 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6667 |
1,3333 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0,4 |
0 |
0 |
|
0 |
|
0 |
0 |
||
|
0 |
0 |
0 |
0,6667 0 |
|
0 |
|
0 |
0 |
|
|
= |
|
|
. |
||||||||
|
0 |
0 |
0 |
0 |
0,2 |
|
0 |
|
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
|
0,8333 |
0 |
0 |
|
|
|
|
|
|||||||||
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0,25 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
|
0 |
|
|
0 |
|
|
0,5 |
||||||||
Аналогічно можна побудувати матрицю жорсткості скінченно-елементної моделі:
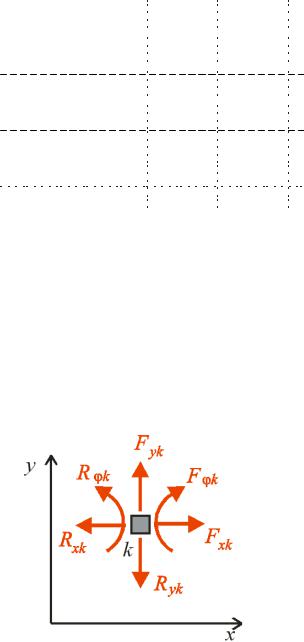
7. МСЕ в формі методу сил |
|
|
|
|
|
|
|
|
13 |
|
|
|
k1−2 0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K = |
0 |
k |
2−3 |
0 |
0 |
|
|
= |
|
|
|
0 |
0 |
|
k3−5 |
0 |
|
|
|
|
|
|
|
0 |
|
0 |
k |
|
|
|
|
|
|
0 |
|
3−4 |
|
|
||||
1 |
|
− 0,5 |
0 |
0 |
0 |
0 |
|
0 |
0 |
|
− 0,5 |
|
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
2,5 0 0 0 0 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
= |
0 |
|
0 |
0 |
1,5 |
0 |
0 |
|
0 |
0 . |
|
0 |
|
0 |
0 |
0 |
5 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
0 |
1,2 0 0 |
|||
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
2 |
|||||||
7.5. Рівняння рівноваги вузлів скінченно-елементної моделі
Усі и елементи и скінченно-елементної и моделі и повинні и перебувати и в и рівновазі. и Умови и рівноваги
скінченних елементів були залучені, коли встановлювався зв’язок між кінцевими реакціями і кін-
цевими зусиллями (п.7.1). Зараз розглянемо умови рівноваги вузлів. Будь-який жорсткий вузол k
скінченно-елементної моделі (рис.7.7) перебуває під дією зовнішніх навантажень, які визначаються
компонентами вектора F , а також сумарними кінцевими реакціями, які передаються на вузол з боку завантажених стержнів.
Рис.7.7
Використовуючи рівняння рівноваги вузла запишемо
∑Fx = 0 Rxk = Fxk ,
∑Fy = 0 R yk = Fyk ,
∑M = 0 Rϕk = Fϕk .

7. МСЕ в формі методу сил |
14 |
При складанні цих рівнянь доцільно перетворити кінцеві зусилля Mi, Mj та N до кінцевих реак-
цій, орієнтованих за осями глобальної системи координат xy.
Кінцеві реакції в місцевій системі координат стержня визначимо через кінцеві зусилля рівнян-
ням
r1′r′2r′
r′ = 3 e r′
4
r′5r′
6 e
−1 0 |
0 |
0 |
0 |
0 Ni |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
Qi |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
M |
i |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||
0 |
0 |
0 |
1 |
0 |
0 |
|
= E (sk )e |
, |
|||
|
N j |
|
|
|
|||||||
|
0 |
0 |
0 |
0 |
−1 0 |
Q |
j |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
−1 M |
|
|
|
|
||||||
|
|
|
|
|
|
|
j e |
|
|
||
або з урахуванням (7.1) у вигляді
′ |
|
|
re |
= E L e |
se . |
Перетворимо кінцеві реакції до глобальної системи координат:
|
= TT |
|
|
|
|
|
|
. |
r |
r |
′ = TT E L |
e |
s |
e |
|||
e |
e |
e |
e |
|
|
|||
У співвідношенні (7.35) TeT − транспонована матриця перетворення:
(7.33)
(7.34)
(7.35)
cosβ |
− sinβ |
0 |
0 |
0 |
0 |
|
|
|
|
sinβ |
cosβ |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
(7.36) |
TeT = |
0 |
0 |
0 |
cosβ |
− sinβ |
0 |
. |
|
|
|
|
||||||
|
0 |
0 |
0 |
sinβ |
cosβ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
e |
|
Після виконання (7.35) кінцеві реакції стержня виражатимуться через кінцеві зусилля, тобто через основні невідомі задачи.
Зазначимо, що вигляд матриці Le залежить від типу скінченного елемента. Для стержня пер-
шого типу матриця визначається залежністю (7.2). Для стержнів інших типів з цієї матриці необ-
хідно виключити той чи інший стовпець. Так, для елемента другого типу
|
|
1 |
|
|
1 |
T |
|
|
|||
L e = |
0 |
− |
|
1 |
0 |
− |
|
|
0 |
, |
(7.37) |
l |
l |
||||||||||
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|||
|
0 |
|
|
||||||||
для третього

7. МСЕ в формі методу сил |
15 |
|
|
1 |
|
|
1 |
T |
|
||||
L e |
= 0 |
|
|
|
1 |
0 |
|
|
|
0 |
(7.38) |
|
l |
|
l |
||||||||
|
|
0 |
0 |
1 |
0 |
|
|
||||
|
1 |
0 |
|
||||||||
і, нарешті, для четвертого |
|
|
|
|
|
|
|
|
|
|
|
L e |
= [1 |
0 |
|
0 |
1 |
0 |
|
0]T . |
(7.39) |
||
Сумарні и реакції, и що и передаються и на и вузол k и скінченно-елементної и моделі и з и боку и прикріплених до цього вузла стержнів, можуть бути виражені через кінцеві реакції стержнів за такими формула-
ми:
Rxk = ∑r1i− j + ∑ r4i− j |
|
|
i=k , j=1,n |
j=k ,i=1,n |
|
Ryk = ∑r2i− j + |
∑ r5i− j , |
(7.40) |
i=k , j=1,m |
j=k ,i=1,m |
|
Rϕk = ∑ r3i− j + ∑r6i− j . |
|
|
i=k , j=1,m |
j=k ,i=1,m |
|
Записавши рівняння рівноваги вузлів у напрямах можливих переміщень вузлів, дістанемо сис-
тему рівнянь рівноваги, яка може бути записана в матричній формі таким чином:
|
(7.41) |
A S = F , |
|
де A − матриця коефіцієнтів рівнянь рівноваги вузлів. Слід зауважити, що різниця між кількістю |
|
|
|
стовпців і кількістю рядків, тобто між кількістю основних невідомих (компонентів вектора S і кі- |
|
лькістю рівнянь рівноваги, характеризує ступінь статичної невизначуваності |
стержневої системи. |
Тобто в статично невизначуваних системах матриця A має вигляд прямокутника, причому кіль-
кість стовпців перевищує кількість рядків.
Приклад 7.3. и Побудувати и матрицю и коефіцієнтів и рівнянь и рівноваги и вузлів и скінченно-елементної
моделі (рис.7.5,в).
Передусім и побудуємо и вектори и кінцевих и реакцій и для и всіх и стержнів и скінченно-елементної и моделі
за формулою (7.35). Величини синусів і косинусів нахилу місцевих систем координат стержнів
можуть бути обчислені за формулами (6.2), довжини – за формулою (6.1).
Так, для стержня 1-2 (l=4, sinβ=1, cosβ=0):

7. МСЕ в формі методу сил |
16 |
r |
|
0 |
- 1 |
0 |
0 |
0 |
0 -1 0 |
0 |
0 |
0 |
0 |
|
0 0 |
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
r2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 0 |
0 |
0 |
0 |
- |
4 |
4 |
|
|||||
r3 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 0 |
0 |
0 |
|
1 0 |
||||||
|
||||||||||||||||||||
r |
|
= 0 |
0 |
0 |
0 |
-1 |
0 |
× |
0 |
0 |
0 |
1 |
0 |
0 |
× |
0 0 |
||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
r |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
- 1 |
0 |
|
||||||
|
5 |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
- |
4 |
4 |
|
||
r |
|
0 |
1 |
- 1 |
|
0 1 |
||||||||||||||
|
6 |
1−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0.25M12 - 0.25M 2−1 |
|
||
|
- N1−2 |
|
|
|
|
||
|
M1−2 |
|
|
= |
|
|
. |
- 0.25M12 + 0.25M 2−1 |
|||
|
N1−2 |
|
|
|
|
||
|
- M |
2−1 |
|
|
|
|
|
Аналогічні обчислення виконаємо для інших стержнів. Зрештою матимемо:
∙ для стержня 2-3:
|
r1 |
|
|
- N2−3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
- 0.1667M 2−3 |
|
|
|
||||||||||
|
r |
|
|
M |
2−3 |
|
|
|
|
|
|
|
||||
|
|
3 |
|
= |
|
|
|
|
, |
|
|
|
||||
|
r4 |
|
|
N2−3 |
|
|
|
|
|
|
|
|||||
|
r |
|
|
0.1667M |
2−3 |
|
|
|
|
|||||||
|
|
5 |
|
|
|
0 |
|
|
|
|
|
|||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6 |
2−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
для стержня 3-5: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
0.16M 5−3 - 0.6N3−5 |
|
||||||||||||
|
r |
|
|
0.12M |
5−3 |
+ 0.8N |
3−5 |
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
r |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
3 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
, |
|
r4 |
- 0.16M 5−3 + |
0.6N3−5 |
|||||||||||||
|
r |
|
- 0.12M |
5−3 |
- |
0.8N |
3−5 |
|
||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
|
|
|
|
- M |
5−3 |
|
|
|
|||||
|
|
6 |
3−5 |
|
|
|
|
|
|
|
|
|
|
|||
∙ |
для стержня 3-4: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
- N3−4 |
|
|
|
|
|
|
|
|
|||||
|
r |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
= |
|
|
. |
|
|
|
|
|
|
|
||
|
r4 |
|
|
N3−4 |
|
|
|
|
|
|
|
|||||
|
r |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6 |
3−4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
M |
1−2 |
|
|
0 |
|
|||
|
|
= |
||
× M |
2−1 |
|
||
1 |
|
|
|
|
|
N1−2 |
|
|
|
0 |
|
|
|
|
0
7. МСЕ в формі методу сил |
17 |
Складаємо рівняння рівноваги за допомогою співвідношень (7.40).
Для вузла 2
∑Fx = 0 r41−2 + r12−3 = F1,
∑Fy = 0 r51−2 + r22−3 = F2 ,
∑M = 0 r61−2 + r32−3 = F3;
для вузла 3:
∑Fx = 0 r42−3 + r13−5 + r13−4 = F4 ,
∑Fy = 0 r52−3 + r23−5 + r23−4 = F5 .
Підставляючи у визначені рівняння компоненти відповідних векторів кінцевих реакцій і вузло-
вих навантажень, зрештою одержимо
−0,25M1−2 + 0,25M 2−1 − N2−3 = 0; N1−2 − 0,1667M 2−3 = −7,5;
−M 2−1 + M 2−3 = 9;
N2−3 + 0,16M 5−3 − 0,6N3−5 − N3−4 = 0;
0,1667M 2−3 + 0,12M 5−3 + 0,8N3−5 = −14,5.
Коефіцієнти при невідомих можуть бути записані у табличному вигляді (табл.7.1):
Таблиця 7.1
№ |
M 1−2 |
M 2−1 |
N1−2 |
M 2−3 |
N 2−3 |
M 3−5 |
N 3−5 |
N 3−4 |
1 |
-0,25 |
0,25 |
0 |
0 |
-1 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
-0,1667 |
0 |
0 |
0 |
0 |
3 |
0 |
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
1 |
0,16 |
-0,6 |
-1 |
5 |
0 |
0 |
0 |
0,1667 |
0 |
0,12 |
0,8 |
0 |
|
|
|
|
|
|
|
|
|
Отже, матриця системи рівнянь набуває вигляду:
−0, 25 0, 25 0 |
0 |
|||
|
0 |
0 |
1 |
−0,1667 |
|
||||
A = |
0 |
−1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
|
||||
|
0 |
0 |
0 |
0,1667 |
|
||||
−1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
. |
||||
0 |
0 |
0 |
0 |
|
1 |
0,16 −0,6 −1 |
|||
|
|
|
|
|
0 |
0,12 |
0,8 |
0 |
|
|
||||

7. МСЕ в формі методу сил |
18 |
7.6. Повна система рівнянь та її розв’язок
Для розв’язання названої задачи рівняння рівноваги (7.41) має доповнюватися геометричними
та фізичними рівняннями, виконання яких забезпечує нерозривність деформацій поміж вузлами і
скінченними елементами скінченно-елементної моделі (п.4.5). Таким чином, повна система рівнянь
будівельної механіки матиме вигляд
|
|
|
|
|
|
A S |
= F, |
|
|
|
|
AT |
= ε, |
|
|
(7.42) |
|
BS = ε. |
|
|
|
||
Два останніх рівняння із (7.42) можна замінити одним фізико-геометричним: |
|
||||
AT |
|
|
|
|
|
|
− BS = 0 . |
(7.43) |
|||
Виразивши через (7.43) вектор зусиль |
|
|
|
|
|
|
|
|
|
|
|
S = B−1AT |
, |
(7.44) |
|||
і підставивши його до рівняння рівноваги можемо знайти вектор переміщень:
|
|
|
|
|
= (A K AT )−1 F . |
(7.45) |
|
Тут враховано, що B −1 = K . Нарешті з (7.44) |
дістанемо вектор зусиль: |
|
|
S = K AT (A K AT )−1 F . |
(7.46) |
||
|
|
|
|
Таким чином, для розв’язання будь-якої задачі достатньо побудувати дві матриці: умов рівно-
ваги A і жорсткості K, а також вектор вузлових навантажень F .
7.7.Обчислення дійсних зусиль у стержнях
Коли вектор зусиль у стержнях системи S обчислено, процедура знаходження дійсних зусиль в окремих елементах системи являє собою технічну процедуру, що включає перетворення незалеж-
них зусиль в стержнях Mi , M j i N до кінцевих і в додаванні до них вантажних реакцій, які вини-
кають у стержнях від дії рівномірно розподілених навантажень:
N |
д = −N − p′ |
, |
N |
д = N + p′ |
, |
||
|
i |
1 |
|
|
j |
4 |
|

7. МСЕ в формі методу сил |
19 |
|
д |
|
|
M i |
|
|
M j |
′ |
д |
|
|
|
M i |
|
|
M j |
′ |
|
|
||||
|
Qi |
= − |
|
l |
+ |
l |
+ p2 , |
Q j |
= − |
|
l |
+ |
l |
− p5 |
, |
(7.47) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
M |
д = |
M |
i |
+ p′ |
, |
|
M |
д |
= |
M |
j |
− p′ . |
|
|
|
|||||||
|
|
i |
|
|
|
|
3 |
|
|
|
j |
|
|
|
|
|
|
6 |
|
|
|
||
У матричній формі наведені залежності мають вигляд |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
д |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(sk )e |
= Le se |
|
|
, |
|
|
|
|
|
|
|
|
(7.48) |
|||
|
|
|
|
|
|
|
+ E p e |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
= {Niд Qiд |
Miд |
|
N дj |
|
Qдj M дj |
} − вектор дійсних кінцевих зусиль елемента. |
|||||||||||||||||
де (sk )дk |
|
|
|||||||||||||||||||||
Нагадаємо, що вигляд матриці Le залежно від типу скінченного елемента визначається співвідно-
шеннями (7.2), (7.37), (7.38) або (7.39).
Приклад 7.4. Побудувати епюри внутрішніх зусиль для рами (рис.7.5).
Виконавши матричні операції згідно з (7.46) |
дістанемо вектор зусиль скінченно-елементної мо- |
||
делі |
|
|
|
|
− 5,121 |
− 6,853 3,879 |
− 2,104 − 2,145 − 18,618 8,719}T , |
S = {3,299 |
|||
тобто M1−2 = 3,299; |
M 2−1 = −5,121; |
N1−2 = −6,853; |
|
M 2−3 = 3,879, |
N 2−3 |
= −2,104; |
|
M 5−3 = −2,145; |
N3−5 |
= −18,618; |
|
N3−4 = 8,719. |
|
|
|
Побудуємо епюри зусиль в стержні 2-3 (стержень другого типу). Згідно з (7.48) можемо запи-
сати, що |
|
|
|
|
|
|
|
|
|
|
N |
д |
|
0 |
1 |
|
|
|
|
|
|
2д |
|
− 0,25 |
0 |
|
|
|
|
|
Q2 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
д |
M д |
|
1 |
0 |
3,879 |
|
+ |
||
(sk )2−3 |
= |
д2 |
= |
0 |
|
|
|
||
|
N |
3 |
|
1 |
− 2,104 |
|
|||
|
|
д |
− 0,25 |
0 |
|
|
|
||
|
Q3 |
|
0 |
0 |
|
|
|
|
|
|
M |
д |
|
|
|
|
|
||
|
|
3 |
|
|
|
|
|
||
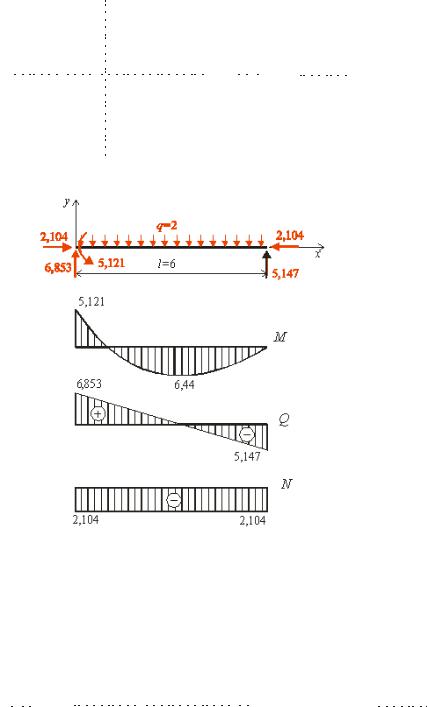
7. МСЕ в формі методу сил |
|
|
|
|
|
|
|
20 |
|||
− 1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
− 2,104 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
7,5 |
|
6.853 |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
- 9 |
|
- 5,121 |
||
+ |
|
|
|
|
|
|
× |
|
= |
|
. |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
- 2,104 |
||
|
0 |
0 |
0 |
0 |
-1 |
0 |
4,5 |
- 5,147 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 |
0 |
-1 |
0 |
|
|
0 |
|
||||
Схема повного завантаження стержня 2-3 і епюри M, Q i N зображені на рис.7.8.
Рис.7.8
Для стержня 1-2 (перший тип) беручи до уваги, що розподілених навантажень немає, можна записати:
(sk )д−
1 2
N |
д |
|
|
1 |
|
- |
|
Qд |
|
||
1 |
|
|
|
|
д |
|
|
= N1 |
|
= |
|
N2д |
|
|
|
Qд |
|
- |
|
|
2 |
|
|
N |
д |
|
|
|
2 |
|
|
0
0,25
1
0
0,25
0
0 |
1 |
|
|
|
- 6,853 |
|
|
|
|
|
|
|
|
0,25 |
0 |
|
|
3,299 |
- 2,105 |
|
0 |
0 |
|
|
|
|
3,299 |
0 |
1 |
|
× |
- 5,121 |
= |
. |
|
|
|
- 6,853 |
|||
0,25 |
0 |
|
- 6,853 |
- 2,105 |
||
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
- 5,121 |
Аналогічно можна обчислити зусилля в стержнях 3-5 і 3-4. Для побудови епюр зусиль у рамі необхідно відкласти відповідні епюри в стержнях на її загальній схемі.

ДО ЗМІСТУ ПІДРУЧНИКА
III. РОЗРАХУНОК СТАТИЧНО
ВИЗНАЧУВАНИХ СИСТЕМ
8.Ферми
9.Тришарнірні арки
10.Плоскі рами
Статично визначуваними називають системи, напружений стан яких може бути визначений за допомогою лише рівнянь рівноваги. З точки зору кінематичного аналізу ці системи не містять надлишкових ("зайвих") з’єднань.
Напружений стан статично визначуваних систем не залежить від жорсткостей елементів. До того ж дія температури та примусове зміщення опор не зумовлюють появу внутрішніх зусиль та напружень.
Для визначення внутрішніх зусиль в статично визначуваних системах здебільшого використовується метод перерізів. Цей метод має різні втілення для різного типу стержневих систем. У даному розділі розглядаються способи обчислення внутрішніх зусиль для плоских ферм,
напружен-деформований стан яких характеризується відсутністю поперечних і згинних деформацій та зусиль у стержнях. Також показано особливості розрахунку тришарнірних арок. В
опорах арок дія вертикальних навантажень зумовлює появу не лише вертикальних, а й горизонтальних опорних реакцїй (розпору), який зменшує згинальні моменти і поперечні сили в тришарнірній арці, порівняно з балкою, а натомість значно збільшує поздовжні сили. І нарешті обговорюється розрахунок плоских рам, як простих, так і складених.
