
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
отж синус ¹ швидкоосцилю чою ункцi¹ю i внаслiдок цього ве- |
||||
личина iнте рала ¹ незначною. Першèé iнте рал запису¹мо через |
||||
перiод коливань |
|
|
p , |
|
сво¹ю чергою |
T = 2m Zx1 |
|||
|
|
|
x2 |
dx |
åíåð i¨ |
T = 2π/ω, ω циклiчна частота, яка залежить вiд |
|||
E, i таким чином ма¹мо, що |
|
|||
|
2 |
T |
|
|
àáî |
|C| |
|
= 1 |
|
4m |
||||
rr
Нарештi, нормована хвильоваC = |
4m |
|
|
|
|
2mω |
|
|
|
|
||||||||||||||||||||||
|
T |
óíêöiÿ= |
|
|
|
. |
|
|
|
|||||||||||||||||||||||
|
|
π |
|
|
|
|||||||||||||||||||||||||||
|
гармонiчногоПрикладψ(x)1=. r πp |
|
cos |
|
|
~ |
|
x2 |
p dx + 4 |
, |
x1 < x < x2. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2mω |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
||
i¨ |
|
|
|
|
армосцилятонiчнийора:осцèлятор. Запишåмо класичний вираз для енер- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
mω2 |
|
2 |
|
|
|
|
|
||||
Його можна переписати так: E = |
|
|
|
|
+ |
|
|
r |
x . |
|
|
|
|
|||||||||||||||||||
2m |
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
p |
|
|
x |
2 |
|
|
|
|
|
|
|
||||
Цей виразцi¹юне |
|
|
|
|
|
|
|
|
ðiâняння |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
åëiïñà â 2координатах= 1. |
|
||||||||||||||||||||
|
|
|
|
|
ùî iíøå,√ |
ÿê |
|
|
2 + |
|
|
|
|
|
( |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
( |
|
2mE) |
|
|
|
|
|
|
2E/mω2 |
|
|
|
|
|
||||||||||
обмежену |
|
|
азовою тра¹кторi¹ю, визнача¹мо розмiрами пiвосейx, p). Площу,елiпса |
|||||||||||||||||||||||||||||
|
√ |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
I |
|
|
|
2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a = 2mE, |
b = 2E/mω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Бора Зоммер √ |
|
|
|
|
|
|
|
|
2πE |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2E |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
p dx = πab = π |
|
|
2mE |
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
mω2 |
ω . |
|
|||||||||||||||||||
З умов квантування |
|
|
|
|
|
|
|
|
|
|
|
ельда ма¹ìî |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πE/ω |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
звiдки й отриму¹мо добре вiдоìi ðiâíi=åíåðn + i¨ ,гармонiчного осцилятора |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π~ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
262 |
|
|
|
|
|
|
|
|
|
|
|
|
E = ~ω(n + 1/2). |
|
|
|
|
|
||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приклад 2. Ангармонiчний осцилятор |x|k . Енер iя тако¨ системи |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
iмпульс |
|
|
|
|
|
|
|
E = |
|
|
|
|
|
+ α|x| |
, |
|
k > 0, |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Умова квантування:Z x2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
p = |
2m(E − α|x|k ). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
äå |
|
|
|
x1 |
|
|
|
2m(E − |
α|x|k ) dx = 2π~(n + 1/2), |
|
|
|
|
|||||||||||||||||||||||||||||||
çàìiíó çìiííî¨ |
|
Z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(E/α) |
1/k , |
x2 |
= (E/α) |
1/k . Зробимо |
|||||||||||||
n = 0, 1, 2, . . ., а точки повороту x1 = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
x = y(E/α)1/k |
. |
|
|
|
|
|
|
|
|
|
|
умова квантування набира¹ вигляду: |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
Тепер |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
4 (E/α)1/k √ |
|
|
|
I = 2π~(n + 1/2), |
|
|
|
|
|||||||||||||||||||||||||||||||||
äå iíòå ðàë |
|
|
2mE |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
çàìiíîþ |
|
|
|
|
|
|
|
|
|
|
I = |
0 |
|
|
|
|
|
1 − yk dy |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
y = t1/k зводимо до B-iнте рала Ейлера |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
t1/k−1 |
(1 − t)1/2dt = |
(1 + 1/k) (3/2) |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
I = k |
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
(1/k + 3/2) |
|
|
|
|||||||||||||||||||||||||||||||||
(z) гаммаункцiя. Остаточно ма¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
α1/k ~ |
|
(3/2 + 1/k)π |
|
|
|
|
|
|
2k/(2+k) |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ченьЗгiднозгквантовогопринципармонiчE числа= âiäï√ |
|
âi (1 + 1/k) (3/2) (¹nточним+ 1/2) прикладуграницi. âå èê õ çíà |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
дностi цей вираз |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ляньмо кiльк |
nк. нкретних випадкiв. При |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
тораенер iю для |
|
|
|
îã |
|
|
|
осцилятора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отримуосциля¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Äëÿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
попередньогоk = 2 очевидно. |
|
|
||||||||||||
x4 |
|
k = 4 çíàõîäèìî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
2α~4 1/3 3√ |
|
(3/4) |
|
|
|
|
|
|
4/3 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
E = |
|
|
π |
(n + 1/2) |
|
|
|
|
|||||||||||||||||||||||||||||||||
Ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
(1/4) |
|
|
|
|
|
|
|||||||||||||||||||
n = 0 звiдси одержу¹мо енер iю основного стану |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
3 |
2α~4 1/3 3 |
|
|
|
√ |
|
(3/4) |
4/3 |
|
|
3 |
2α~4 1/3 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ïîðiвняти |
|
|
|
√ |
|
ç |
îöiíêîþ |
знизу дëÿ |
|
|
|
× 1.156194. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
m2 |
|
||||||||||||||||||||||||||||||||||||||
E = |
8 |
m2 |
|
|
|
|
|
12 |
|
|
|
|
|
(1/4) |
|
|
|
= |
8 |
|
|
|
||||||||||||||||||||||
Öiêàâî |
|
|
|
цей вираз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
êëàäiÄëÿ2äî |
Ÿ7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E, яку ми знайшли в При- |
|||||||||
|
|x| -осцилятора (k = 1) åíåð iÿ |
|
|
|
|
|
|
|
|
|
|
|
|
263 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лазбiга¹ться з т ч им результатом з Ÿ241/3 |
при великих значеннях квантового чис- |
|||||||||||||||||||||||||||
|
|
|
|
|
E = |
|
~2β2 |
|
|
|
|
|
|
|
3π |
(n + 1/2) |
2/3 |
|
||||||||||
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n; äëÿ îñíîâíого стану (n = 0) наш квазiкласичний вираз да¹ |
||||||||||||||||||||||||||||
|
|
|
|
|
~2β2 1/3 |
3π |
2/3 |
|
|
|
~2β2 |
1/3 |
× 1.115460, |
|||||||||||||||
записуточний числ вий êîå iöi¹íò äîðiâíþ¹ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
E = |
2m |
|
|
8 |
|
|
|
|
|
|
= |
|
|
|
|
2m |
|
|
|
|
|||||
|
|
|
îзгляньмо великi значення показник. частинки |
|
||||||||||||||||||||||||
Нарешстiнкпри |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.018793 |
|
|
|
|
||||||||||
¹ìî |
àê: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k. Для цього величину α |
|||
резуль атi |
|
α = V0/x0k , V0 масшт б енер i¨, x0 масштаб довжини. В |
||||||||||||||||||||||||||
високими |
kàìè→ ∞i шириноюприхдимо |
|
|
|
|
çàäà÷i ïðî ðóõ |
в ямi з безмежно |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
a = 2x0. При цьому енер iя |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
~2 |
|
π |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
åâàëåíêтроналонiвськийовихчислахатомiззточноюотенцiальноюормулоюенерз Ÿ20i¹ю. |
||||||||||||||||||
ЦейПвиразкладзбiг3.¹тсяАтомприводнювеликихE.= óõê |
|
|
a |
|
|
(n + 1/2) . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Uсиметрпе= −e |
2 |
/r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
площинi,ент льнощо |
ðèдикучному, унаслiдокярнп ю (другийзаконувектора,законзбереженняКеплермоменту),вiдбув(першийiм ¹тьсяульсув |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
електронахар ктерзаконпотенКеплера)iалу забез.Кi- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íèéминатах |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
|
||
ïåтичначу¹ рухенеректроiя електроназапишемоелiптичнимилярних. КуорбiтУведемооор |
|
|
|
|
|
|||||||||||||||||||||||
í |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ä |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2/2 = m(r˙ + r2ϕ˙ 2)/2, |
|
Крапкамиr довжипозначенорадiупохiднiс- |
часомϕ ïîëÿ. |
|
|
|
|
утанонiчно(0 ≤ r <спряженi∞ 0 ≤iмпульсиϕ ≤ 2π). |
||||||||||||||||||||||
pr = mr˙, pϕ = mr2ϕ˙ |
|
|
|
повну енер iю |
|
|
|
|
у такому виглядi: |
|||||||||||||||||||
Узагальн ний iмпульс |
E = |
pr2 |
|
+ |
|
|
pϕ2 |
|
|
|
− |
e2 |
. |
|
|
|
||||||||||||
2m |
|
2mr2 |
r |
|
|
|
||||||||||||||||||||||
|
|
åëüäà:äâà |
ступенipϕ вiльностiчисельноI |
|
дорiвню¹отже, двiмоментовiумови кiлькостiквантуванняруху БораL. |
|||||||||||||||||||||||
ЗоммерМа¹мо |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
I pϕ dϕ = 2π~nϕ, |
|
|
|
|
|
||||||||||||||||
å |
|
|
|
|
|
|
|
|
pr dr = 2π~nr , |
|
|
|
|
|
|
|||||||||||||
азимутальне квантове число, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
æèìî,nϕ що ми опуска¹мо |
правих |
|
|
астинахnr умоврадiальневантуванняквантовестумовачислоiвел.Зауваини- |
||||||||||||||||||||||||
νäîðiâíþ¹óìîâϕ νr (0ÿ≤õâνϕльово¨< 1, 0 ≤ νr |
< 1)Для,то дновимiрнiзначенняогояких |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
óíêöi¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рухузалежать,якмибачили,вiд гранцяè÷сталаних |
||||||
Âåëичина1/2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вання да¹ |
pϕ ¹ iнте ралом руху |
pϕ = const. Тому перша |
êâàí ó- |
|||||||||||||||||||||||||
264 |
|
pϕ = ~nϕ, nϕ = 1, 2, 3, . . . . Çíà |
|
|
|
|
|
nϕ = 0 ми повиннi вилучиòè, |
||||||||||||||||||||

|
öå âiäï âiä๠ðóховi електрона по прямiй лiнi¨ крiзь ядро ( маятни- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
оскiлькиова орбiта), |
ùî, |
за класичними уявленнями, неможливо. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Другу умову квантування запишемо так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Z r2 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pϕ |
|
|
|
|
|
|
|
|
dr = 2π~nr , |
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
r1 |
|
|
2m E − 2mr2 + |
|
r |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
nнулевir = 0,пiдкореневого1, 2, . . . |
rвиразу,1 r2 точкирозв'язуючиповороту,приякiцьомувизнач |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
. Òóò |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратне¹мо з уморiвняння:и рiвностi |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
= |
|
me2 |
(1 |
|
|
|
|
ǫ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1,2 |
|
|
r |
pϕ2 |
|
|
|
± |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ǫ = |
|
|
|
|
1 + |
2Epϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ексцентриситет елiпса. Тепер пiдкореневий4 вираз |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
E |
|
|
|
|
|
|
pϕ2 |
|
+ |
e2 |
|
= |
|
|
|
|
pϕ2 |
|
me1 |
|
|
|
1 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
− |
2mr |
2 |
|
r |
|
−2m r |
|
− r1 |
|
r − r2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
i для обчислення iнте рала зробимо замiну змiнно¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
π |
1 |
|
|
Z π |
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
r |
= |
2 |
|
Z |
|
r1 |
+ |
r2 |
|
|
|
+ |
2 |
|
|
r1 |
|
− |
r2 |
|
|
|
cos ϕ, |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ïðè |
, |
|
|
|
|
|
|
|
|
|
|
|
ïðè |
r = r2 |
. Якщо використкван ування:изчення |
r1 |
, |
r2, òî |
|||||||||||||||||||||||||||||||||||||||||||
ϕíàøà= 0пiдстановкаr = r1 |
ма¹ϕ =вигляд:π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Простi перетворення дають для друго¨ умови |
|
|
|
2ò |
|
|
2 åëiïñ. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
r = p/(1 + ǫ cos ϕ), p = pϕ/me |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Iнте ру¹мо частинами: |
|
pϕ |
|
|
|
|
π |
|
|
|
|
ǫ2 sin2 ϕ |
|
dϕ = ~nr . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
0 |
|
|
|
(1 + ǫ cos ϕ)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
pϕ |
|
|
ǫ sin ϕ |
|
|
|
|
|
|
|
− |
|
|
|
|
|
ǫ cos ϕ |
|
|
|
= ~nr , |
|
|
|
|
|
||||||||||||||||||||||||||||||||
i îòæå, |
|
|
π |
|
|
|
|
|
|
1 + ǫ cos ϕ |
|
|
|
|
|
|
|
|
1 + ǫ cos ϕ |
dϕ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
pϕ |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
àáî |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ = ~nr |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
π |
|
0 |
|
|
|
1 + ǫ cos ϕ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пiдстановкою |
|
|
|
|
|
|
|
|
|
|
|
pϕ |
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
|
= pϕ + ~nr . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
0 |
|
|
|
1 + ǫ cos ϕ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Z |
|
x = tan(ϕ/2) цей iнте рал приводимо до табличного: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
π |
dϕ |
|
|
|
|
|
= |
|
|
|
|
|
|
2 |
|
|
|
Z |
|
∞ |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|||||||||||||||
0 |
1 + ǫ cos ϕ |
|
|
|
1 − |
|
ǫ r0 |
|
|
|
1+ǫ |
|
+ x2 |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1−ǫ |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 − ǫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − ǫ |
|
|
|
|
π |
|
|
. 265 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctan |
|
|
x |
|
|
= |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
|
ǫ |
|
|
|
|
1 + ǫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + ǫ |
|
√ |
1 − ǫ |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||

Îòæå, |
|
|
|
|
|
|
|
|
pϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Звiдси, пiдставляючи |
|
|
|
|
|
|
= pϕ + ~nr . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 − |
ǫ |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
ǫ, знаходимо енер iю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
me4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тобто ми отримали ормулу |
EÁîðà= −ä2(pϕ |
+ ~nr )2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ëÿ ðiâíiâ åíер i¨ електрона в атомi водню: |
|||||||||||||||||||||||||||||
äå |
|
|
|
|
|
|
|
|
|
|
|
|
|
E = − |
me4 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2~2n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nЯкщо= nr +взяnϕ и= до1, 2уваги, 3, . . .i сталiголовневеличиниквантове числоiквантування. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νϕ = 1/2 |
|
|
òîî çàìi |
èò |
nr |
íà |
nr |
+ 1/2, nr |
= 0, 1, 2 . . . , nϕ |
íà l + 1/2 |
, |
|||||||||||||||||||||||||||||||
νr = 1/2, òîá |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
умову . |
|
|
|
|
через по- |
|||||||
l âiéíèé= 0Повчально, 1, 2iíòå. . ., ралтакголîæâíерозрахуватиквантоZ Z числорадiальнуn = nr |
+ l + 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
де межi радiально¨ координатиdr dpr = 2π~(nr + 1/2), |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
åíåð i¨, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r при заданому pr знаходимо з виразу для |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
2 |
|
|
me2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
me2 |
|
pr2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
à ìåæi äiàëüíо¨ компоненти= |
|
iìïó |
ëüñó |
|
pϕ |
|
− |
+ 2mE, |
|
|
|
||||||||||||||||||||||||||||
|
|
rmin,max |
|
pϕ2 |
|
|
|
± |
pϕ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
âîãî âèðàçó: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pr знаходимо з нуля цього пiдкорене- |
|||||||||||||||||
pZr =Z±me2ǫ/pϕ. Îòæå, |
|
iíòå ðàë |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
ǫ/pϕ |
rZmax |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
meZ |
|
|
|
|
meZǫ/pϕ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
dr dpr = |
|
|
|
|
|
|
|
|
dpr |
dr = |
|
|
|
|
|
dpr (rmax − rmin) |
|
|
||||||||||||||||||
|
|
|
|
|
|
−me2 ǫ/pϕ rmin |
|
|
|
−me2 ǫ/pϕ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
meZǫ/pϕ |
|
|
|
|
|
|
|
|
|
|
|
me2 |
|
|
− pr2 + 2mE |
|
|
|
|
|
|
|
||||||||||||||
|
= 2pϕ |
|
|
|
|
dpr |
|
|
|
|
|
|
pϕ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
pr2 − 2mE |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
−me ǫ/pϕ |
|
|
|
|
me2ǫ |
|
|
|
|
|
|
|
|
Zπ/2 |
|
|
cos2 x |
|
|
|
|||||||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
sin x = 4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
çàìiíà |
pr = |
|
|
|
|
|
|
|
ϕb |
|
|
dx |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
pϕ |
|
|
|
1 + b sin2 x |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
! |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pme2 |
|
|
|
|
|
|
|
||||||
òóò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 , |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= 2πpϕ 1 + b − 1 = 2πpϕ |
|
|
pϕ |
|
2m|E| |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
, |
|
попередньогоТепер,виразу дляумовиенерквантуванняi¨. при |
pϕ = |
(l + 1/2) |
||||||||||||||||||||||||||||||||||||
266приходимоb = (meäîǫ) /pϕ2m|E|. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ÿ 31. |
|
|
механiка |
iíòå ðàëè çà |
àê |
хвильова |
||||||||
|
ßê |
|
квантова механiка айзенбер |
||||||||||||
таннi гамiльШрединКвантоваового ормалiзму. Iншими словтра¹кторiямими, операторнi |
|||||||||||||||
механiкматрич |
|
åðà |
ðóíòуються значною мiрою на викорис- |
||||||||||||
рiвняння руху |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
i хвильове рiвняння |
|
üñiâ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
класичнiй |
ˆ ˆ |
ˆ ˆ |
|
|
|
|
|
|||
|
|
|
|
|
|
dA |
|
|
|
|
|
|
|||
|
|
|
|
|
|
~ dt |
= AH |
− HA, |
|
|
|
|
|
||
|
|
|
|
|
|
|
∂ψ |
|
ˆ |
|
|
|
|
|
|
використовують оператор ~àìiëü=òîíàHψ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
àìðàiè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ââå |
|
|
|
|
|
|
|
|
|
|
|
|
знiбуяннявiдповiдноюпiдхякого¹багатьлощепок.диамiльАналогмидне,азанохдовипаддоповописутонатрет¹пере |
||||
|
|
|
|
|
|
|
|
|
|
|
ðíàöå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оператори |
|
|
|
|
|
|
класичнiй¹люванмивiдповiднодинальненихвжерiвняанiчниходногоязна¹мо,зквантово¨класично¨ьiмпурiвняння.Виявля¹явищцiдва,мехункцi¨òздаваламiльанiки,ься,ематичнооордимехщодоамсьнаiцi,можливимвикладуби,¹льна,тякеквiвалентнимиякий |
|
|
|||||||||||
|
òузагь.овомех |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дених |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iше,оюормухЯкбуду¹т |
|
|
|
|
|
|
H |
|
|
|
|
|
|||
íàâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нююкванЯкобi |
|
|
|
|
|
|
|
|
|
|
|
|
|||
õ äèìî. |
ìåõ |
|
iцi, крiм гамiльтонового пiдхо |
äî ïîáó |
|
||||||||||
|
Ó |
|
|
|
|||||||||||
ви рiвнянь руху, ¹ ще |
д Ла ранжа, ий рунту¹ться на |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
ÿê ункцi¨випадкдузагальненихвонадорiв |
|||||
|
|
|
|
ранжметоанерй.Уi¨найпростiшому |
|
|
|
|
|||||||
ню¹координатденнiрiзницiункцi¨ткiнетично¨швидкостЛа L = L(x,˙ |
x, t) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
K |
потенцiально¨ енер i¨ U : |
|
|
|||||
вмiрномуЯкмоментзавжди,прочами |
|
|
|
L = K − U. |
|
|
|
|
|
|
|||||
|
|
мiнiмальностiуторiдля.Нехайпростотичастинкарозгляда¹мопочина¹рухсвiйчастинкирухздякво¨дновиточки- |
|||||||||||||
З принципу |
ta |
завершу¹ його в iншiй точцi в момåíò ÷àñó |
tb. |
||||||||||||
|
|
äi¨ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = Zta b L(x,˙ x, t) dt, |
|
|
|
267 |
|||||

тобто з умови δS = 0, знаходимо рiвняння Ла ранжа3
|
d ∂L |
∂L |
|
|
Ëà ðàíæà |
i ункцi¹ю амiльтона вiдомий: |
|
Çâ'ÿçîê ìiæ óíêöi¹þ |
dt ∂x˙ − |
∂x |
= 0. |
|
L = px˙ − H, |
||
|
p = |
∂L |
|
|
∂x˙ |
|
|
|
|
|
|
нiповiднотому,швидОдндокторськiйзнаючипостiтiм завждиперейти, можнавда¹тьсдоузагквантово¨цимярiвняннямакзадачiпросто. розрахувативиразитиузагальнеiвiд |
|||
L |
|
|
H |
x˙ через |
àë íåíi |
iмпульси p, тобто рiвнякий |
|
ймовiрностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хвикорисладнак,. .низкТомуогоЦейСамепiдхзааiдбува¹тьсшляхвиуважити,вувавакихíсклада¹тьакуåдуикзцiкавийа¹ранiшеметузадач,бипринципомпотребдисертнещогмавтим,намiльертацi¨самуприклад,даввинайтищо.суперпозицi¨тонiвсвПüiдею,.порядсяА.варiантМуявномубезпосередньслаборелятивiс.кийДiракiзякийаквантовимикласичнавiншляхтично4виг.побулядiористову¹дувасновнiво¨ласькiйамплiтутеорi¨ранжiвання,у 1942ормумех.акi.тiСлiд,дам™ïiä |
|||||||||||||||
p = ∂L/∂x˙ |
|
|
|
Фейнман, |
|
x˙ = x˙ (p) |
анронацiли-- |
||||||||
очнi поняття, як |
|
|
|
|
äiÿ, òèì |
àìèì |
|||||||||
|
è÷íi òðà¹êòîði¨ |
|
|||||||||||||
iíòó¨òè íî |
ñя враження нiбито бiльшо¨ зрозумiло |
|
òî |
|
|||||||||||
ãî,3 ùî |
â |
|
ÿ â |
|
|
. |
|
|
, óâiâ |
içèêó Ï'¹ð |
|||||
Принцип найменшо¨ дi¨, або варiацiйний |
|
||||||||||||||
Ферма (1601 1665), р нцузький математик |
iзик, приблизно в 1660 роцi. |
||||||||||||||
Çãiäíî ç öèì |
|
мiкросвiтiло поширю¹ться вiд точки до точки по шляху |
|||||||||||||
потребу¹ найме шого часу: природа дi¹ на |
егшими т найдоступнiшими |
||||||||||||||
шляхами. Пiзнiше, |
насту них |
ñòîëiòòÿõ, öåéпринциинцип розробляли |
|
|
- |
||||||||||
тю¨, Ейлер, Лапринципом,ра ж, амiльтон. Його |
|
i виняткова роль у |
|||||||||||||
iз цi стали |
|
ïiñëÿ |
|
|
üöà, Ï àíê |
Íåò |
|
. Öiê |
|
|
|||||
велсамек |
понятт дi¨ ввiв ще |
|
. У XVIIIунiверсальнiстьрiччi цей принцип викликаво, |
||||||||||||
|
авлення, особ |
иво iлосо ського погляду. П.-Л. М. де |
Мопертю¨див цей |
||||||||||||
(1698 1759) вбачав |
ць му осно у теологiчнельмгого свiтоглядуа,вiн |
|
|||||||||||||
принцип ( Нариси Косм |
|
гi¨ , 1750 .) як доказ iснування Бога, |
уважаючи, |
||||||||||||
рештзацiкдоказiвзрозумiлимибу безсилимиЛяйбнiцнепереконливими. |
äèâ., |
|
|
|
éîãî |
||||||||||
4Ïðî öå íåî |
|
|
|
робiтсам . Фейнман; |
|
|
|
||||||||
щоН362белiвську(1948). лекцiю,дноразовотакговоривж статтю: R. Feynman, Rev. Modнаприклад,. Phys. 20 No. 2,
268
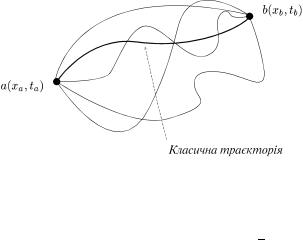
Уведемо амплiтуду ймовiрностi того, що частинка з точки |
xa |
||||||||||||
в момент часу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ta перейде |
точку xb в момент часу tb |
|
||||||||||
òàê ùî éìîâiðíiñòü òKàêò(îãîb, a)перех= K(xäó, t |
; x |
a |
, t |
a |
), |
|
|||||||
|
|
|
|
|
b |
b |
|
|
|
|
|
||
|
|
|
éìîâiðíiñòü |
|
|
2 |
|
|
|
||||
якВикориста¹момибачили, тойхвильоваP (,b,óíêöiÿùîa) = |Kквазiкласичномувизнача¹ться(b, a)| . класичноюнаближеннi,дi¹ю |
|||||||||||||
S = S(x, t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ S(x t) |
|
|
|
|
||||
чинитра¹кторi¹юБудемо постулюввизнàча¹тьсяти,щоψ(x,амплiтудою,t) e такогояка. пропорцiйнаперехдузадодеякоювели- |
|||||||||||||
|
|
i |
i |
tb |
|
|
|
|
|
|
|
|
|
|
e |
|
S = exp |
~ |
Zta |
L(x,˙ |
x, t) dt . |
|
|||||
|
~ |
|
|||||||||||
Повнаис.31.амплiтудаМожливi шляхиймовiрностiперехду частинки з точки a в точку b.
K(b, a) = зара¹кторiямивсiмаXжливимиза const × e ~i S ,
a b
Síå=ëèøåS[x(tçà)] класичноютобто беремотра¹кторi¹юсуму (диввсiма. рисмислимими.31). шляхами,269а

Ó |
випадку |
макросêопiчно¨ системи на баг |
|||||
то порядкiвкласичномупере |
ищузмiню¹квантдiя ¨ ~ = 1.05457266 · 10−27 ã· |
ñì /ñå , |
|||||
чають2 |
|||||||
S/öiÿñ ~швидк1. Тосцилюючим |
i |
омпенсуютьсзначення,вiдтих алетра¹кторiйязмiню¹( унк- |
|||||
âнески вiдмножникомсусiднiх тра¹кт рiй, що визна |
|
|
|||||
нак!)практично5. Т вiдмiннийне вiдсвогонулячисельноговнесокS ,ëèøå |
|
|
|
||||
|
|
e ~ |
|
|
|
|
|
çмiню¹тьс, дляварiацiяякихпеðшомупереходiнаближедоiíшихнiзасусiднiх |
x(t) + δx(t) |
äiÿ |
S |
íå |
|||
x(t) |
|
|
|
|
|
||
|
|
δx(t): |
|
|
|
|
|
тобто |
S[x(t) + δx(t)] = S[x(t)], |
|
|
|
|
||
дорiвню¹ нулевi, |
δS = S[x(t) + δx(t)] − S[x(t)] |
|
|
|
|||
ЦекiлькиваютьУ принципкласичнiвантовiйнайменшо¨рiвняннясистемiвнескирухудi¨δS.класичнiй=âñiõ0. тра¹кторiймеханiцi,¹сумiрнимзякоговèïëè,îñ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
близькiму Тльнiшеàкимвсiматра¹кторi¨,чином,ц.можливимийперехiдуквантовiйсума.шляхамиозiб'¹мозамiню¹тьсеханiцi.часовийЯкщнеяiнтебхiднорозглядатиiнтервалраломвраховувати.озглянембезмежносу |
||||||||||||||
äåò |
S |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âiäïîâiäíiñòü |
|
|
|
|
|
t |
|||||
x¹òüñ=Äëÿx(t ) íà òðà¹êòîði¨íà x(t), |
через |
ïðîìiæзначенняокчасукоординатиε вiдбува- |
||||||||||||
люючо¨5 змiщення |
|
x |
|
|
òðà¹êòîðiþ |
x(t) + δx(t) |
tb − ta íà N |
|||||||
однакових елåментарних iнтервалiв величиною |
ε, |
|||||||||||||
|
|
|
|
âiçüìiìî |
|
|
|
|
|
бачити, що внаслiдок цих |
||||
|
|
|
|
I = ∞ e−x2 cos νx dx. Ëåãê |
||||||||||
як цеСтавимозображеноу наε =ðèñt |
. 32ìà¹ìî.tê, жномуε = |
− |
ta |
, |
|
|||||||||
|
|
|
|
|
+1 − |
|
tb |
|
|
|
||||
|
|
|
|
|
моментовi часу |
|||||||||
осциляцiй270 |
|
|
|
|
|
N |
|
|
|
|||||
I = √π e−ν2/4 |
→ 0 |
ïðè ν → ∞. |
|
|
|
|
|
|||||||
оординати x . ßêùî ìè |
|
|
в момент t |
|
|
|
значення |
|||||||
|
óíêöi¨ëàäó |
|
|
iíте рал у безмежних гр |
èöÿõ âi(äившвидк. рис.осци33). |
|||||||||
|
ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
ïå÷ó¹ éîãî çáiæíiñòü:cos νx, ν → ∞, помножено¨ на повiльну ункцiю, що забез-
R
−∞

ис. 32. озбиття часового iнтервалу на елементарнi промiжки.
Перебираючи таким чиномîìóсi можливi тра¹кторi¨, амплiтуду ймовiрностi запису¹мо в так виглядi:
|
|
|
|
|
Z |
|
|
|
|
|
Z |
|
|
|
|
~ S[x(t)] |
|
|
|
||||
IнтевiдповiдноралK(b, a) =óíêöi¨lim constЛа ранжа,dx |
...ÿêèédxвизнача¹e |
äiþ |
|
||||||||||||||||||||
|
ε |
→ |
0 |
|
× |
|
|
|
1 |
|
|
|
N −1 |
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S[b, a] = |
|
b |
до нашого розбиття часового iнтервалó çàìiíþ- |
||||||||||||||||||||||
¹ìîL dt,сумою |
|||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
xj+1 |
|
xj |
|
|
|
xj+1 + xj |
|
tj+1 |
+ tj |
|
|
|||||||||
чення координатикрайнiхчасу |
мiж точками з номерами |
||||||||||||||||||||||
причомуS[b,çíàa] = ε |
j=0 |
L |
ε− |
|
|
|
, |
|
|
2 |
|
, |
|
|
2 |
|
, |
|
|||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
j + 1 беремокiнцi пiвсуму |
|
|
|
|
|
|
значень x → (xj+1 + xj )/2, |
||||||||||||||||
t → (tj+1 + tj )/2, |
тра¹кторiйшвидксть |
|
як середню |
швидкiсть |
x˙ → |
||||||||||||||||||
. Iíòå ðóâ ííÿ çà |
|
оординатами |
|
|
|
|
|
|
|
= xb |
|||||||||||||
не проводимо:Якщоiнтервал |
|
|
|
|
|
çà óìî |
оютра¹кторi¨:закрiпленими. |
||||||||||||||||
(xj+1 − xj )/ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
= xa |
|
xN |
||||
всi можливi моментиε спрямуватичасувсiмодожливiнуля, |
|
|
|
|
переберемо |
||||||||||||||||||
|
|
|
|
|
1 |
dx |
1 |
|
|
|
|
dx |
N −1 |
|
i |
S[x(t)]. |
|
|
|
||||
Ми розбилиK(b, añò) àëó= limâåëè÷èíó |
|
|
... |
|
|
e |
~ |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
ε |
0 |
A Z |
|
A |
|
|
|
Z |
|
A |
|
|
|
|
|
|
|
|
|||
|
|
N → |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
const на добуток сталих величин |
||||||||||||||||
1/A, якi нам треба б де ще визначити. |
|
|
|
|
|
|
|
|
|
|
271 |
||||||||||||
