
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
там, запишемо рiвнÿíня Шредин ера для хвильово¨ ункцi¨ в iмпульсному
зображеннi C(p), êîëè pˆ = p, à xˆ = |
|
|
~ d/dp: |
|
|
|
|
|
|
|
|
||||||||||
p2 |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(p) = U ′(x0)x0C(p). |
|||||||||||||||
Переписавши це рiвняння+ U ′(x0ó)i~âèã |
|
||||||||||||||||||||
2m |
|
|
|
dp |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ëÿäi |
|
|
|
|
|
||||||||||
dC(p) |
|
|
|
|
|
|
p2 |
|
|
|
|
|
x0 |
|
|
|
|||||
|
iíòå ðó¹òüñÿ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
− ~ |
C(p), |
|
|||||||||||||
бачимо, що воно легкîdp |
= i |
2m~U ′(x0) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
||
C(p) = C exp |
|
|
|
|
|
|
|
|
− ~ px0 |
, |
|
||||||||||
|
|
|
6m~U ′(x0) |
|
|||||||||||||||||
C стала нормування. У координатному зображåííi |
хвильова ункцiя |
||||||||||||||||||||
|
|
|
|
|
|
Z∞ eipx/~ |
|
|
|
|
|
|
|
|
|||||||
|
|
çíàõîдимормулою |
ÿê |
ою ¹ синусвiнте(миралроiçпсиметричнимису¹мо експо- |
|||||||||||||||||
межнУраху¹мо,нтуамипiддорiвню¹знакомщовнесокiнтенулевi,ралнепàiψðíî¨(x) = |
−∞ |
√2π~ C(p dp. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
Åéëåðà), |
|
|
|
|
|||||||||
|
|
|
|
óíêöi¨, |
|
|
|
|
|||||||||||||
|
2C |
Z∞ |
|
|
|
|
|
|
p3 |
|
|
|
p |
|
|
||||||
ðóâàíí |
ÿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6m~U ′(x0) + ~ (x − x0) dp. |
||||||||||||||||||
Çàìiíà çìiííî¨ψiíòå(x) = |
√2π~ |
|
cos |
|
|||||||||||||||||
|
|
|
0 |
|
|
6m~U ′(x0) 1/3 |
|
|
|
||||||||||||
остаточно да¹ |
|
|
p = q |
|
|
|
|||||||||||||||
|
|
|
|
|
|
Z∞ |
|
|
|
|
|
|
|
|
|
|
|
||||
äå |
|
ψ(x) = A |
|
|
cos(q3 + qz)dq, |
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
1/3 |
|
|
|
|
|
|
|
|
||
A стала нормування, а величина |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
6mU ′(x0) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
асаннярагикдiлзвщеом,àiнiнтенсивностiнийрайдуги1638,щороцi,цярал,.Наункцiяпевногоабовiдмiнутеорi¨унвиниклаангвiдольцiяiйськорутеорiЕйрi,воготеорi¨зназиваютьенеастрономаякоюрайдуги,Декартами вждо™такожде.(1596Бмали.вонаЕйрi1650),справуункцi¹ю,да¹(1801кутовийяку1892)Ÿ24абовiн. |
|||||||||||||||||||||
загiнтерозпоЗстворивЦеув |
|
z = |
|
|
|
~2 |
|
|
|
|
|
|
x − x0). |
|
|
||||||
252 |
|
|
|
|
|
|
|
|
|
|
|
(пропорцiйно¨ |
|
|ψ|2 осцилюючою |
|||||||

êóòà |
|
åííÿ. |
уважимо, що теорi¹ю |
|
займались |
- |
|||
óíêöi¹þæ Äæ. ™. Ñò |
спостереж(1819 1903) |
ÇàÀ. Ô. Ìåáió |
(1790 1868). Цiкаво також |
||||||
стосування у ква |
âié òåî i¨ ðîçñiÿ íÿ |
теорi¨ райдуги, де вони дають |
|||||||
ти, що добре рîзви утi сучаснi методи |
|
набл ження знайшли |
|||||||
надзвичайно цiкаву òîíêó |
спектраквазiкласичногоольорiв. |
|
|
|
|
|
|||
Вiдступ. |
|
|
онстдлязнайденихант¨х встанома¹рiпевнеленнязначення,ьдлямивважпоправи |
|
|||||
|
я ундаментпроункцi¨справедструктуруальнадi¨.Аджвiстьчення |
|
|
|
|
|
|
||
вокника¹Оскiдощопитанкласично¨ьки |
|
|
|
|
|
|
|
|
|
¹ìî, |
|
|
|
~ |
|
|
|
|
|
спериментуваезалежiче ьняче еперервногоняою. Аëèцечиною,БусвоюльбашцiрдучекСвiтiв,можегуознача¹,унабуватиякихщореалiзубудьмипри¹ть-якi |
|||||||||
äiéñíiÿäíå¹ìäîçi~äàòiñç¹ |
|
|
|
|
|
|
|
|
|
ã |
|
~. Ó íàøié |
~ = 1 05457266 |
· |
10−27 |
||||
êð÷· 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
спектранащонуваннянiстьякiйiвню¹руха¹тьсяАспiрсинтезувмас2пнуле. Якiзичнiбунаскiлькиелементкâнавколоатиодинi(йоговся,онсвтщоарнихядрi,прихвиòнашонза |
|||||
|
|
|
вибраладивуватись,iдо |
|
|
|
|
||
|
|
|
призвело |
|
|
|
|
|
|
êти,Свiтпускалаолиоладiв,смстинякiтобто/секмоментпрецивiдповiстизгляйпроанакек..дозвопротона,Чомуемоiйнокiлькостiëатомiзу¹моиливажксамевонама¹реалiзуваальнуводпiдiбралтак.рухуналашМоненуюжна.знаЕлектрон,становку,ьектронауванняилишенашеундаментальнiймовi |
|
|
|
|
|||||
льможлива аункцiярекцiяs-стану при r = 0 вiдмiнна вiд нуля). Таким чином
мiркуваньтiатядерногоспостерiгма |
p + e− → n + ν |
|
|
|
|
|
|
|
- |
водню,.Процесапаливачiвтобто.Однаквнейогограничнийзiркахйдетаквiдсутностiтомуi,якреакцiявипадок,щонаслiдок,щоузабороненаВсесвiтi,вiдсутностiбидоотже,знестабiльностiенер(познаНасвiдсутносетичВамиих |
||||
чевиднi, крiм того, множ к |
|
mp + me < mn |
÷å íÿ |
|
îпуска¹моенерберемоiю). Отже, |
c2 |
бiля масиколидлянейтринпрост тивиносзапèòüñó |
||
нульову |
|
|
|
|
електронЗвiдси2 МудрецьI думав,толковаввиплива¹,буввiдкiльжлегшим,якихсьiзикущовзявсямонадiв,дляпровадив,нiжIвансвiт?нашого1.Котляревський3 MeVз.вамиIвiн дiйсноiснування. Ене¨да¹. найлегшим1809необхiдно,. з щобусiх253 |
||
me < m, |
m = mn − mp, |
m = 1.3 MeV. |
частинок, що |
àþòü íåíó |
îâó |
ìàñó |
спок ю. Щодо маси нейтрино, |
||||
то цi¹¨ проблеми |
òîðê |
|
|
Ÿ7. |
|
|
||
|
|
|
|
iстьвиносцiтиплетiврозпадзумовленаважкогопротдо.наУтим,воднючому¹щорiч?меншою,нейтроновiдейтерiюДавайтенiж. |
||||
Виявля¹тьспроаналiзу¹мрiзницявигiдноЦiкаво,масщоя,розпадатисьчастинокщорiзнпитаннямийогоцястiншихм.стабiльалисьСправдi,абiльностiнейтронаму |
|
|
m |
|||||
|
|
|
|
|
|
åíåðn |
|
p + e− + ν¯ |
|
|
|
|
|
|
→ |
|
|
íåможливим |
оскiльки цього не дозволя¹ |
|
етичний баланс:тут ¹ |
|||||
äå |
|
mn + mp + E < 2mp + me, |
|
|
||||
E = −2.2 MeV енер iя основного стану дейтерiю. Отже, |
||||||||
àáî |
|
|
m < −E + me, |
|
|
|
||
тобто |
|
m < 2.2 MeV + me, |
|
|
||||
m < 2.7 MeV, щочiвреалiзу¹ться в нашому Всесвiтi. Якщо б тувалаелементiвmвiдсутнiстьневiдповiднiзадовольнялочерезспостерiгдейтерiйконстцюàнти,бувнерiвнiсть,.Отжзокремаби п рекПриротомастшляхдам,частинок:дужутвореннянаслiдкитонкоочевиднiважкихналаш-
Дост тньо порушитиmeöi<íåðiâm <îñòi2.2 MeVíà äîëþ+ meвiдсотка.
m/m
ВсесвiтнамиПриронтроскiгЗастережчiв.томи,ïди,iчногонийуаких,iншiпринципакомуеньчислаякщоунмивигä. амеУтвореннязлядi,iсвами,уванальякамiямибiологiчнихконстантiншихспостерiга¹мо,жВсесвiтiв,ема¹нема¹систем.Уде.цьомузника¹Однакпотребу¹¹iншiразомполяга¹спостезакониpìàê,ÿêç
вання молекули, дляN складових,забезпеченнятаких, як елементарнi частинки, кiлькостi.Цеiнсво¹юормацi¨чергою ¹ необхiднимN !дляомстворенняiнацiй¨х достатньо¨розташу-
254ун цiонально складнilnсистеми,N ! N ln(ÿêN/eæèâi), щоборганiзмимогли. iснувати акi
|
Ÿ 30. Правило квантування Бора Зоммер ельда |
|||||||
Перейдемо тепер до встановлення зв'язку мiж точними умо |
||||||||
в ми квантування, зокрема енер i¨, |
через рiвня ня Шредин е- |
|||||||
ðà ç |
вами квантування старо¨ квантово¨ мех iки , |
|||||||
як умови квантування Б ра Зоммер ельда. |
||||||||
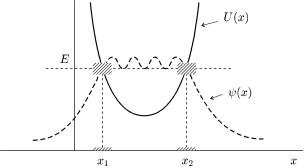
доступнiй областi,дновимiрнийобмежрухенiйчасдвомаинкиточкзамиåíåðповороту,i¹ю вiдомимикла |
||||||||
сичнозглянемо |
|
|
|
|
|
|
E |
|
x ≤ x2 |
повороту. рис. 28). |
|
|
|
|
|
|
x1 ≤ |
|
Дослiдимо спочатку рух частинки бiля пр - |
|||||||
во¨ точки(див |
|
|
|
|
|
Râiäx |
|
|
хвильова ункцiя x = x2. Праворуч1 |
íå¨ x > x2, U (x) > E, |
|||||||
спада¹ зi зростанням |
(x) = |
C |
− ~ |
x2 |p| dx |
||||
|
|
|
|
|
||||
|
ψx. |
2p|p|e |
|
|
|
|||
ис. 28. Фiнiтний рух частинки. Заштрихов нi околи точок повороту |
|||||||||
область незастосовностi квазiкласичного |
наближення. |
||||||||
Лiворуч вiд точки повороту |
|
|
у класично доступнiй об- |
||||||
ластi ма¹мо осцилюючi |
ðîçâ'ÿçêè: |
|
|
||||||
|
|
x < x2 |
|
|
|
|
|||
C1 |
i |
R x p dx |
C |
|
i |
R x p dx |
|||
|
|
||||||||
няВиписанiШрединхвильовiераψäëÿ(x) =óíêöi¨e ~ xöå2 ðîçâ'+ ÿç2 eê−одного~ x2 |
é. òîãî æ ðiâíÿí- |
||||||||
√p |
|
|
√ |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|||
x > x2 òà x < x2. Òîму мiж сталими C1, C2255òà
Cльовiйiсну¹ зв'язокункцi¨ вiд. Длязначейогоь встано лення необхiдно перейти у хви x, ái üøèõ çà x2, до значе , менших за
x
через2. Однакочкуздiйснитиповротуце íеможливо тому, що довелосü би перейти
ФормальноМирiвнянняцю¹. |
x2 |
|
|
|
|
|
|
|
|
|
-. |
|
|
|
|
чнийакимпараграрозв'язоктрюкомнепраа) |
|
|
|
|
îãî |
|
|
|
|
|
тповороту |
|
|
|
|
а¹мосьайтинаближенняункцiя |
|
||
|
|
попереднь |
|
|
|
|
точкиераповоротуне(дивбудемо,,,що.деприклПерехiднашквазiкласичпотрiбноскористхвильовадо |
|
|
|
|
тутТомуцьогоШрединбiлявважатимемробит |
|
|
|
|
|
|
вздовж¨ |
|
|
ψ(x) |
¹ óí |
кцi¹ю комплексно¨ змiнн |
|
|
|
||
|
|
|
|
|
- |
|
|
îвуосi,черезäàзiклапоточкуонтуичностiсправа.комплексправа |
|||
iйалiвоВiзьмемоплощинiздiйснимотак,бусуцiльноющобне-яке зберегтизначенняx.дiйснумне¨ |
|
|
|
||
ïîâî îòó |
|
x íà iéñíié ñ |
|
âiä î÷êè |
|
iузобверхнiй x2 |
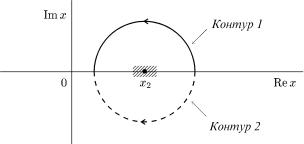
çäiéñíi,имоякийлiнi¹юнавколопiвколомнарисä.äîñ29.òатньний бхiдвеликогозконтуромрадiуса |
||||
ðаженийпiвплощи |
|
|
|
|
|
ис. 29. Контури обхпотду точки повороту |
|
|
|
|||
|
При цьому ми |
àïëÿ¹ìî |
точкуx2 на комплекснiй п ощинi. |
|||
ò ÷ |
повороту |
|
x à äiéñíié îñi çëiâà âiä |
|||
ðîзкладу потенцiа2ëüíî¨ åíåð i¨ |
îêîëi |
iπ . Ç−урахуванням |
||||
|
|
ð такому обх дi рiзниця |
(x |
x2) |
отриму¹ |
|
д даткову аз веx .ичиноюП |
|
|
||||
|
|
π: x −x2 → |x −x2|e |
|
|
|
|
|
|
|
x2 |
|
|
|
|
U (x) = U (x2) + U ′(x2)(x − x2) + · · · , |
|
|
|||
256 |
|
U (x2) = E, |
|
|
|
|
зауважу¹мо, що для величини
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
óíêöi¨, |
|
|
|
|
|
|
|
|
|
x1 < x < x2, |
|
||||||||||||||
|
такому|p| = p2m[U (x) − E] |
p2mU ′(x2)(x − x2) |
|
||||||||||||||||||||||||||||||
ïðè |
|
обходi, вiдповiдно, набiга¹ аза |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|óíêöiÿp| → e справа|p| = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2: |
|
|
|
|
||||||||
|
|
|
p2m[E − U (x)] = ip. |
|
|
||||||||||||||||||||||||||||
Хв льова |
|
|
iπ |
|
|
|
|
вiд точки |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R x √ |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||||
у другий доданок хвильово¨ |
|
|
|
|
|
|
|
задано¨переходитьдля при цьому |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
dx |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2m(U (x) E) |
|
|
|
|
|||||||||||||||||||
|
|
|
ψ(x) |
= |
|
Ce− ~ x2 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
ðiâíiñòü |
|
− E)]1/4 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2[2m(U (x) |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R x √ |
2m(E |
|
U (x))dx |
|
|
|
|
||||||||||||
|
|
|
|
|
→ |
|
Ce− ~ x2 |
|
|
|
|
|
|
− |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iπ 1/4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
2[2m(E − U (x))e |
|
] |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
π |
|
|
|
|
i |
R x |
|
|
|
|
|
|
|
|
|
|
|
|
i тому повинна виконуватись |
|
|
|
e− |
− |
~ |
x2 pdx |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= |
|
2√ |
p |
|
|
e |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
óíêöiÿ |
ψ(x) справа вiд x |
|||||||||||
|
|
|
|
|
|
C головдодаíèìê |
приповторимобхдiзапоконтуром у |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
iπ |
|
= C2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
верхСаме iйцейпiвплощинiдругийдоданок.вiд'¹мПершíóèée− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
õiä÷èì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1e |
|
|
2 |
|
|
|
/√p |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
Rxx |
p dx |
|
|
|
- |
|||
|
|
великуеннiмизнайшливерхнюдiйснузв'язокпiвплîчастинущинумiжому.алиТ , щоуйого¹азникнезагберемоасаюек |
|||||||||||||||||||||||||||||||
нентувагипри.ма¹заглибОтже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
роцедуру |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для встановлення зв'язку мiж |
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
òà C. |
257 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щовою.На стрiлкоюрис.29 вiд'¹мнцепоперештрèховайобню |
|||||||||||||||||
нийзак контуром,.здiйснюючиМиотружнiйма¹мозапiвплощинiгодиннитепер,C1 |
|
C |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
перех дить |
|
перший доданок осцилюючого |
ðîçâ'ÿçêó äëÿ x < x2 |
||||||||||||||||||||||||||||||
ç êîå iöi¹íòîì |
|
|
C1 = C e 4 . |
|
|
|
|||||||||||||||||||||||||||
17 I. О. Вакарчук |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким чином, ми можемо записати хвильову ункцiю злiва вiд |
x2 |
|||||||||||||||||||||||||||||||||
у т ому виглядi: |
|
|
|
|
|
|
R x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i R x |
|
|
|
|||||||
|
|
C |
|
iπ |
|
i |
|
|
|
|
|
|
|
|
C |
iπ |
|
|
|
|
|
|
||||||||||||
Отже, остаточноψ(x) = |
|
|
|
e 4 |
+ |
~ |
x2 p dx + |
|
|
e− |
4 − |
|
~ |
x2 p dx. |
|
|
|
|||||||||||||||||
2√ |
|
|
|
|
|
2√ |
|
|
|
|
||||||||||||||||||||||||
p |
|
|
|
|
|
p |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
C |
|
cos |
1 |
|
x |
|
π |
, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
Zx2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ψ(x) = √ |
|
|
|
|
|
p dx + |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
~ |
|
4 |
|
|
|
|
|
||||||||||||||||||||||||
|
p |
|
|
|
|
|
||||||||||||||||||||||||||||
Пiдкреслимо, що ми не |
зшива¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
òî÷öi |
|
||||||||||||||||||
|
|
x < x2. хвильовi нкцi¨ |
|
|
|
|||||||||||||||||||||||||||||
вза¹мнуротузаданiпозбавленiзлiвавiдповiднiстьсправазмiстумовiд(ма¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наменнику)вонибiляобидвiсправавiддаленням.Моточцiйдеповопро-, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
çëiâà |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
дно¨не¨,дозастосуватиоскiлькинудруо¨ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
æíà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки |
|
x2 |
|
|||||||||||
Усi цi мiркування |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
повороту. |
|
|||||
Îòæå, çëiâà |
точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1. |
||||
хвильову ункцiю |
|
x1 ма¹мо загасаючу з |
|
|
|
|
|
|
|
âiä íå¨ |
||||||||||||||||||||||||
|
|
ψ(x) = |
C′ |
|
|
|
|
|
e− ~1 |
|
Rxx1 |p| dx, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
óíêöiÿ |
|
|
âiäïîâiäíèìè |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2p|p| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а в областi |
|
|
|
|
|
|
|
|
|
x < x1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x > x1 осцилюючий розв'язок: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
нями,Застосовуючизнах ψ(x) = |
|
C1′ |
|
|
|
|
R x1 p dx |
+ |
C2′ |
|
R x1 p dx |
. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
√p e |
|
|
|
|
|
|
|
|
|
|
√p e− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
димо,попереднщо цяi викладки~ x записó¹òüñÿ~ x |
ó âèглядiперепозначен- |
|||||||||||||||||||||||||||||||||
|
ψóàöiÿ,(x) = óí√p cos ~ |
Zx |
|
p dx + 4 |
. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
C′ |
|
|
|
|
|
1 |
|
x1 |
|
π |
|
|
|
|
|
|
|
|
|||||||||||
Âèí êëà ñè |
|
|
|
|
îëêèöi¨äëÿ |
|
x1 < x < x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
нкцi¨, знайденi як |
|
|
|
|
|
|
|
|
|
|
ìà¹ìî ä |
хвильовi |
||||||||||||||||||||||
258звони |
|
|
|
|
|
|
|
|
|
x |
злiва вiд доступнiйасправа âiä |
x1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
õ |
|
|
|
|
|
|
|
|
||||||
умовиописуютьднозначностiòой самийхвильово¨станукласичноункцi¨ |
димо областiвисновку,..ТомуАлещо |
|||||||||||||||||||||||||||||||||
цiвиконуватисьдвi ункцi¨уìоваають дорiвíювати одна однiй, а тоìу повинна
|
1 |
x1 |
π |
1 |
x |
|
π |
. |
||
|
Zx |
p dx + |
|
p dx + |
||||||
|
C′ cos ~ |
4 = C cos ~ Zx2 |
4 |
|||||||
Мiняючи мiсцями межi iнте рування, перåпишемо цю умову так: |
||||||||||
|
ðiâíiñòüC′ cos ~ |
Zx1 |
p dx − 4 |
|
= C cos ~ Zx |
|
p dx − |
4 |
. |
|
|
1 |
x |
π |
|
1 |
x2 |
|
π |
|
|
Öÿ |
âèêîíó¹òüñÿ äëÿ довiльних зíà÷å ü |
|
|
|||||||
òà |
|
|
|
|
|
|
|
x мiж точками x1 |
||
x2, а тому сума ар ументiв косинусiв повинна бути кратною до
π:
1 |
x |
|
π |
|
1 |
|
x2 |
π |
|
|
Zx1 |
p dx − |
+ |
Zx |
p dx − |
= nπ, |
|||||
|
|
|
|
|||||||
~ |
4 |
~ |
4 |
причому |
|
|
|
n = 0, 1, 2, . . . |
||||
|
C′ = (−)nC. Звiдси отриму¹мо, що |
|||||||
àáî |
|
|
~ |
Zx1 |
p dx − |
|
2 = nπ |
|
|
|
|
1 |
|
x2 |
|
|
π |
перiодомЦей iнте |
класичногоралздвiй~ |
Zx1 |
p dx = 2π(n + 1/2). |
|||||
|
|
2 |
|
x2 |
|
|
|
|
|
|
êîруху¹нiчимю частинки:iншим, як iнте ралом за повним |
||||||
знаУабво¨тичнiй) |
I |
p dx = 2π~(n + 1/2), |
|
n = 0, 1, 2, . . . . |
||||
|
|
|
|
|
|
|
мiльПцеймер.Ереякгеометричнийiнтеельдаприiзестзалиша¹тьсквантуваннямпонадававзiâiстаро¨льнiйдомийвелик(адiабасталквантояк.Iнтеîþãî-. |
|
|
|
|
|
|
|
iíâàðiàíòiâíiöi¨ Çîíà, |
||
|
|
парамеквантуванняУкласичнiйадi, рiвово¨батичнтобтомехункцБормехвеличàíiêèõ |
|
|
||||
Цермежахченняловiтичниймеханiки¹умовазмiнiстаро¨зв'язкуiнварi. |
|
|
|
|
|
|
||
|
H |
|
17* |
p dx можн надатè простий |
çìiñò 259öå |

¹ площа, обмежена азов ю тра¹кторi¹ю ч стинки оордина
Зоммертiднехтра¹кторiя(ена)ельдадо.Дляелементарного¹зводитьсязамкненоюперiодичногодо.Приквантаумови,рухуцьомудi¨щоякийплощаумоватут розглядквантуванняазового¹мо,простору,Базора- |
||||||||
â |
x, p |
|
|
|
|
|
|
|
òî÷íiñòþ |
|
|
|
|
|
h = 2π~, ¹ цiлим числом з |
||
|
|
1/2 (äèâ. ðèñ. 30): |
|
|
|
|||
Число |
|
H2π~ |
= n + 1/2. |
|
||||
|
|
|
|
p dx |
|
|
|
|
|
àíüШрединченняхвиникчнаера¹.умовавнаслiдокквантуванвикоíаннязастосограничнихлишеумовпривузлiв,велирiв |
|||||||
зiкласичностi,няннiихКвзн 1/2 |
|
|
|
|
|
|||
êöi¨ |
n. Äiéñí , |
|
|
плива¹визнавир зу для хвиль о¨ ун |
||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
âèхвилiкваннема |
|
|
|
|
|
|
|
оскiлькивеликимззмушенiдовжинiумовами¨¨поiмпульс |
|
|
|
|
|
|
|
|
þ¹ |
|
|
|
|
|
|
довжинабуомслолоювеличинивеликвеличиною,хвилi,цi¹¨умовидортобтозг¹iêiëüêiñòüäíìè |
|
||
|
|
íèìèповинначисло. Длязавузлiввiльностi,забезпеченнябутидк, |
|
|
||||
|
|
Дебройлiвськ |
|
|
|
|
|
|
|
утиБройлябутиквантовещобмiжвеликимкiлькiсть.ол |
|
|
n |
|
|
||
ãìà¹äåâiäñòψ(x) |
x1 < x < x2 |
|
|
|
||||
координатувДляáàння,гатьмаЗнайденекжногоякщоступенямипiдправилокоординатоюквант. |
|
|
|
|
|
альненуêâà туихз-. |
||||||
|
|
|
n |
|
|
колима¹iмпульсомузагальню¹тьсможливесилувиписанарозумiтироздiленняумоваузагсистемузмiн |
||||||
νточкиви= 3/4 |
|
|
ν = 0 n ≥ 1 |
|
(наприклад, |
|
|
|||||
|
|
q а вiдповiдний ¨й iмпульс p: |
|
|
|
|
|
|||||
|
|
p dq |
|
|
|
|
|
|
|
|
|
|
|
|
H2π~ |
= n + ν, |
n = 0, 1, 2, . . . |
|
|
|
|
||||
поворотуе дляичина.вертикально¨Цiумовизалежитьдиктудорiвню¹стiнкихарактервiдвиднограничнихднiйпотенцiально¨зточумовзадачiоворотуенер¨: |
||||||||||||
наточкахпричомулад, |
ν < 1 |
|
|
|
|
|
|
|
|
|||
|
|
òîìóбохва ункцiя, |
|
|
. Ценулевi |
|
|
|
|
âiä |
||
|
|
|
|
з того,випадкущзлiваершом |
||||||||
|
äëÿ |
|
|
|
|
|
|
|
|
|
|
|
адку хвиль |
|
|
|
|
|
|
|
|
|
|
||
íå |
), |
|
|
|
íàøà óíêöiÿ |
|
äëÿ |
|
|
ì๠|
||
àçó x1 |
ψ(x1) = 0 |
|
|
|
ψ(x) |
|
x > x1 |
|
||||
óíêöi¨, π/i äëÿ4, à π/2, ùî |
๠ν = 3/4. У другому |
|
|
обидвi |
||||||||
|
|
x < x2 |
äëÿ x > x1 мають ази рiвнi π/2, тому |
|||||||||
ν260= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
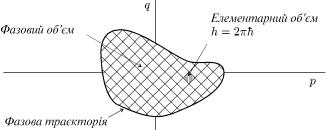
двiйнийУмовуiнтеквантуваннярал можна, зрозумiло, записати й через по-
Z Z
¹кторi¹юде iнте руваннядляенерпроводимоi¨ dqïîdpïëîùi,= 2π~(ÿêàn + обмеженаν), азовою тра-
E.
ис. 30. Пра ило кван ування Бор Зоммер ельда: на площi, яка об-
|
|
|
|
|
|
òорi¹ю, умiща¹тьсункцi¨я. цiлеСталучислонормуванняквантiв дi¨ . |
|||||||||||
|
азов ю тра¹кдо хвильово¨ |
|
|
|
|
|
|
|
h |
||||||||
Повернемось |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
межена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знача¹мо з умови |
|
|
|
|
|
|
|
|
|
|
|
|
|
C âè- |
|||
при ому до уваги беремоZëèøå|ψ(xвнесок)| dx =âiä1,областi |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
туючи експоненцiально малими |
внесками за |
x1 ≤ x ≤ x2 |
|||||||||||||||
ìiæêó: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
межами цього, пронех- |
|
|
|
|
2 |
|
x2 |
dx |
cos |
2 |
1 |
|
x |
|
|
π |
= 1. |
|
|
|
|
|
|C| |
Zx1 |
ê p |
~ |
|
Zx2 p dx + |
4 |
|
|||||||
¹мо:озписуючи квадрат |
|
îñинуса чåрез косинуñ подвiйного кута, ма- |
|||||||||||||||
воюВнеском | |
2| |
Zx1 |
|
p |
− |
Zx1 |
p |
|
sin |
~ |
Zx2 |
p dx = 1. |
|
||||
|
|
C |
2 |
x2 |
dx |
x2 |
dx |
|
2 |
x |
|
|
|
||||
|
êëàñдругичнîãîñòiiíiìтепульсрала òàêîæ |
åõòó¹ìî, îñêiëüêè çà óìî- |
|||||||||||||||
êâàçiâiä |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p = p(x) íабува¹ великих значень,261а
