6251

методов – методы малого параметра), поэтому эти методы хорошо «работают» только при незначительном отличии рассматриваемой системы от соответствующего линейного аналога.

Рассмотрим нелинейное уравнение второго порядка1

где φ – произвольная аналитическая непрерывная однозначная дифференцируемая нелинейная функция, µ – постоянное, малое по величине число (это и есть малый параметр).

При µ=0 уравнение (2.3.28) превращается в линейное

имеющее решение

где частота колебаний ω=1, а амплитуда A определяется начальными условиями.

Эксперименты показывают, что в реальной системе (то есть при≠ 0), описываемой уравнением (2.3.28), возникают автоколебания с частотой, близкой к единице, но всё же не равной ей, и амплитудой, независимой от начальных условий и определяемой параметрами системы.

1 Этим уравнением описывается, например, ламповый генератор с мягким режимом возбуждения колебаний.

111

Естественно предположить, что решение уравнения (2.3.28) можно представить в виде суммы решения приближения нулевого порядка x0 и бесконечных малых добавок

где x1, x2 и т.д. – решения приближений соответственно первого, второго и т.д. порядков.

Разложим функцию φ в ряд Тейлора в окрестности точки (x0, xɺ0 ), обозначив приращения x − x0 = ε, xɺ− xɺ0 = δ

В соответствии с выражением (2.3.31) отклонения ε и δ равны

Подставляя выражения (2.3.33) в формулу (2.3.32), а затем вместе с обозначением (2.3.31) в уравнение системы (2.3.28), получим

112

Приравнивая сомножители при µ в одинаковых степенях в правой и левой частях последнего соотношения, получаем бесконечную систему теперь уже линейных уравнений

... .

Последовательно решая эти уравнения, начиная с первого, получаем добавки x1, x2 и т.д., формируя, таким образом, окончательное решение (2.3.31).

На первый взгляд, этот метод позволяет получить неограниченную точность, но в действительности часто ряд, полученный в результате решения уравнений (2.3.34), плохо, даже качественно, отражает реальную ситуацию при больших значениях t. Рассмотрим это на следующем примере.

Пример 2.3.3. Задано уравнение нелинейной системы

Нелинейность φ, как следует из сравнения уравнения (2.3.35) с уравнением (2.3.28) равна ϕ(x, xɺ)= (a − bx2 )xɺ . Решение уравнения нулевого приближения (первого из уравнений системы (2.3.28)) с начальными

условиями x0(0)= A, xɺ0(0)= 0 есть x0 = Acost , следовательно, правая

113

часть уравнения первого приближения (второго из уравнений системы (2.3.28)) равна

(2.3.31) – нулевые.

Поскольку вынуждающая сила в уравнении (2.3.36) имеет составляющую, производная которой совпадает с общим решением однородного уравнения (2.3.29), то есть с cos t , то в решении для x1 будет составляющая с бесконечно нарастающей амплитудой t cos t . Таким образом, решение уравнения (2.3.36) можно представить в форме

x1(t)= φ11(t)+tφ12(t),

где φ11 и φ11 - гармонические функции.

Поскольку амплитуда решения x1 непрерывно нарастает, будет нарастать и амплитуда приближенного решения

xпр(t)= Acost + µφ11(t)+ tµφ12(t).

114

Следующее приближение x2 даст более точное решение на большем промежутке времени, но оно по-прежнему непригодно для исследования установившихся процессов, поскольку содержит уже член с t2

xпр (t)= x0 (t)+ µx1(t)+ µ2 x2 (t)= Acost + µφ11(t)+ tµφ12 (t)+

+ µ2φ21(t)+ tµ2φ22 (t)+ t2µ2φ23 (t).

Приведённый пример показывает, что не всегда уравнения (2.3.34) дают решение, соответствующее поведению реальной системы.

Члены с возрастающей амплитудой, то есть содержащие множители t, t2 и т.д., называются вековыми или секулярными. Если мы хотим, чтобы найденное решение уравнения (2.3.35) действительно отражало бы характер реального процесса, вековые члены должны исчезнуть. Вековой член в решении x1 пропадёт, если в правой части уравнения (2.3.36) коэффициент M при sin t обратить в нуль. Это условие даст уравнение для

A. Но самое неприятное, что следующее уравнение (для x2 ) приведёт к уравнению, противоречащему первому. Поэтому избавиться от вековых членов подобным образом не получится.

Для поисков методов борьбы с вековыми членами следует, прежде всего, разобраться в причинах из появления. Дело в том, что ряд (2.3.31), получающийся в результате решения уравнений (2.3.34), дает гармонические функции частот, кратных частоте решения нулевого приближения, то есть единице. Однако точное решение уравнения (2.3.35) отличается от решения нулевого приближения не только несинусоидальностью, но и

– самое важное – частотой. Реальная частота колебаний не равна единице

115

ω ≠ 1 , и эта даже небольшая разница с течением времени приводит к всё

бо́льшим отличиям получаемого решения от реального процесса. Ляпунов и независимо от него Рэйли предложили несколько видоиз-

менить составление уравнений (2.3.34). Они предложили частоту нулевого приближения взять равной не единице, а некоторому неизвестному

Далее процедура известна – раскрываем скобки и приравниваем множители при µ в одинаковых степенях в правой и левой частях полученного выражения. В результате получаем бесконечную систему линейных дифференциальных уравнений

116

... .

Последовательно решая уравнения (2.3.39), получаем все больше и больше членов ряда (2.3.31). Частотные поправки hk вычисляются из условий равенства нулю вековых членов последовательно по всей цепочке уравнений. Попутно узнаём всё точнее неизвестную частоту ω в соответствии с формулой (2.3.37).

2 . 3 . 9 . Гар мо ническая линеар изация

Метод гармонической линеаризации предложили Н.М. Крылов и Н.Н. Боголюбов в 1934 г. В приложении к САУ этим методом занимались Л.С. Гольдфарб и Е.П. Попов. В учебной и технической литературе встречаются и другие названия этого метода – метод гармонического баланса, метод описывающих функций, метод эквивалентной линеаризации.

Рассматриваемый метод применяется для определения условий возникновения и параметров автоколебаний, а, следовательно, и определения областей устойчивости и неустойчивости. Кроме того, гармоническая линеаризация может быть применена для исследования вынужденных колебательных режимов и переходных процессов при медленно меняющихся воздействиях.

По-прежнему представляем систему состоящей из нелинейного звена

117

с характеристикой ϕ(x)и линейной части, заданной передаточной функ-

цией W(s) (рис. 2.27).

W(s)

−

y

φ(x) x

Рис. 2.27. Нелинейная система

Применение метода гармонической линеаризации основано на предположении о том, что в системе существуют автоколебания, более того, колебания на входе нелинейного звена являются моногармоническими

где x0 – постоянная составляющая, A – амплитуда, а ω – частота автоколебаний.

На самом деле автоколебания в нелинейной системе не являются моногармоническими вследствие искажения сигнала нелинейным звеном. Но предположение о моногармоническом сигнале на выходе линейной части (или на входе нелинейного звена, что одно и то же) основано на факте, что в большинстве случаев линейная часть является фильтром нижних частот (гипотеза фильтра). Это означает, что амплитуды высших гармоник много меньше, чем амплитуда основной частоты ω . Поскольку частота автоколебаний ω выясняется только в результате применения метода гармонической линеаризации и заранее неизвестна, проверку гипотезы фильтра возможно провести только в конце исследования. Если в

результате такой проверки гипотеза фильтра не подтверждается, к полу118

ченным результатам следует подходить с осторожностью и, по возможности, провести дополнительное исследование каким-либо другим методом.

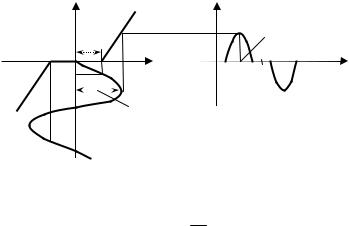
На выходе нелинейного звена сигнал уже не будет моногармоническим из-за нелинейных искажений (на рис. 2.28 показан пример прохождения синусоидального сигнала через усилительное звено с зоной нечувствительности).

Поскольку сигнал y на выходе нелинейного звена периодический, можно разложить его в ряд Фурье, а так как через линейную часть проходит только первая гармоника (гипотеза фильтра), то имеет смысл интересоваться именно этой гармоникой. В результате получим

2π

Рис. 2.28. Искажение сигнала нелинейным звеном

где постоянная составляющая y0 = 1 2∫πϕ(x)d(ωt), а коэффициенты 2π 0

Фурье С1 и С2 вычисляются по известным формулам

119