Шарпан М.В. Математика и информатика

1.1 Множества

Понятие «множество» является одним из основных неопределяемых

понятий математики. Под множеством понимают совокупность (собрание,

класс, семейство, коллекция, ... ) некоторых объектов, объединенных по какому-либо признаку. Так можно говорить о множестве студентов института, о множестве точек отрезка, о множестве вершин

четырехугольника, о множестве корней уравнения x2 + 3x − 4 = 0 , о

множестве всех натуральных чисел и т. д.

Объекты, из которых состоит множество, называются его элементами.

Множества принято обозначать заглавными буквами латинского алфавита

A, B, C,... , а их элементы – малыми буквами a, b, c,...

Запись a A (читается: a принадлежит A ) или A a (читается: A

содержит a ) означает, что a есть элемент множества A . Записи a A ( a не

принадлежит A ) означает, что a не является элементом множества A .

Множество может содержать любое число элементов, конечное и

бесконечное.

Множество, не содержащее ни одного, элемента, называется пустым и

обозначается символом .

Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство,

действительных чисел, удовлетворяющих неравенству 0 ≤ x ≤ 3 .

Для графического (наглядного) изображения множеств и их свойств ис-

пользуются диаграммы Эйлера – Венна (Леонард Эйлер (1707-1783) – швей-

царский математик, механик и физик; Джон Венн (1834 - 1923) – английский

2

логик). На них множество отождествляется с множеством точек на плоскости, лежащих внутри некоторых замкнутых кривых, например окружностей (так называемые круги Эйлера).

Множество A называется подмножеством

множества B , если каждый элемент множества A

B

является элементом множества B (обозначение – B A

или A B ).

Если одновременно A B и B A , т.е. множества A и B состоят из

3

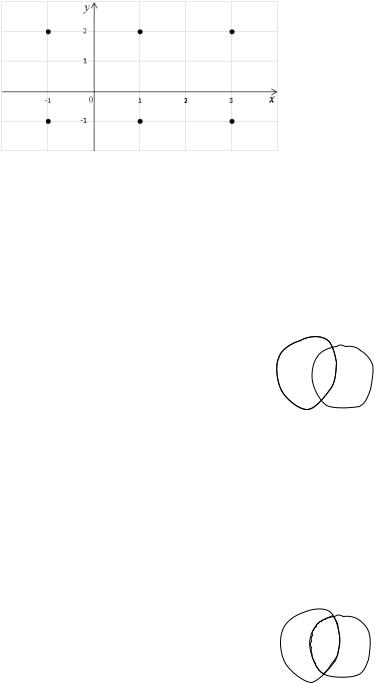
Рисунок 1.

2. Пусть даны два произвольных множества A и B . Объединением множеств A и B называется множество C , состоящее из элементов,

принадлежащих или множеству A или множеств B или множеству A и B

одновременно.

элементов, которые принадлежат множеству A и не принадлежат множеству

B .

4

B \ A.

Решение.

A\ B = {-1; 2;3}\ {0; 2;5;6} = {-1;3}, B \ A = {0;2;5;6}\ {-1;2;3}= {0;5;6}.

5.Пусть даны два произвольных множества A и B . Симметрической разностью множеств A и B называется множество C , включающее все элементы множеств A и B , и не содержащее элементы принадлежащие

одновременно обоим этим множествам.

Пример 7. Для множеств A = {-1; 2;3} и B = {0; 2;5;6} вычислить A B .

Решение.

ADB = (A È B) \ ( A Ç B) = {-1;0; 2;3;5;6}\ {2} = {-1;0;3;5;6}.

6. Пусть дано произвольное множество A . Дополнение множества A –

это множество всех элементов, не принадлежащих множеству A .

U

Универсальное множество U , как правило, изображается множеством точек некоторого прямоугольника.

Для множеств существует понятие мощность. Для конечных множеств мощность совпадает с количеством элементов.

Пример 8. Вычислить мощность множеств A = {O/ }, B = {−1},

C = {− 2;0;1;3}.

5

Решение.

Множество A не содержит ни одного элемента, следовательно, A = 0 .

Множество B содержит один элемент, следовательно, B = 1.

Множество C содержит четыре элемента, следовательно, С = 4 .

1.3 Свойства операций над множествами

Пусть дано универсальное множество U . Тогда для любых множеств

A, B, C ( A, B, C Í U ) справедливы следующие свойства множеств:

1.Если A Ì B и B Ì C , то A Ì C (транзитивность);

2.Если A Ì B и B Ì A , то A = B ;

3.Если A Ê B , то A È B = A ;

4.Если A Ê B , то A Ç B = B ;

5.A È A = A (идемпотентность объединения);

6.A Ç A = A (идемпотентность пересечения);

7.A ÈU = U (свойство единицы);

8.A ÇU = A (свойство единицы);

9.A È Æ = A (свойство нуля);

10.A Ç Æ = Æ (свойство нуля);

11.A \ A = Æ ;

12.A È B = B È A (коммутативность объединения);

13.(A È B)È C = A È (B È C ) (ассоциативность объединения);

14.A Ç B = B Ç A (коммутативность пересечения);

15.(A Ç B)Ç C = A Ç (B Ç C ) (ассоциативность пересечения);

16. A È (B Ç C) = ( A È B) Ç ( A È C) (дистрибутивность объединения

относительно пересечения);

17. A Ç (B È C) = ( A Ç B) È ( A Ç C) (дистрибутивность пересечения

относительно объединения);

18.A \ (B È C) = ( A \ B) Ç ( A \ C) ;

19.A \ (B Ç C) = ( A \ B) È ( A \ C) ;

6

20.(A Ç B)È A = A (поглощение);

21.(A È B)Ç A = A (поглощение);

22.A = A (свойство двойного дополнения);

23.A È B = A Ç B (закон де Моргана);

24.A Ç B = A È B (закон де Моргана);

25.A È A = U (свойство дополнения);

26.A Ç A = Æ (свойство дополнения);

27.A \ B = A Ç B .

1.4 Числовые множества

Множества, элементами которых являются числа, называются

числовыми. Рассмотрим примеры числовых множеств, а также установим связи между ними.

Решение.

а) Множество натуральных чисел: {1; 6}.

б) Множество целых чисел: {− 4; 0; 1; 6}.

7

г) Множество иррациональных чисел: {tg3; ln 5; e; π }.

1.5 Счетные множества

Конечное множество – множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k , равное количеству элементов этого множества. В противном случае множество называется бесконечным.

Счетное множество – это бесконечное множество, элементы которого возможно пронумеровать натуральными числами.

Свойства счетных множеств

1. Любое подмножество счетного множества не более чем счетно (т.е.

конечно или счетно).

2.Объединение конечного или счетного числа счетных множеств

счетно.

3.Прямое произведение конечного числа счетных множеств счетно.

4.Множество всех конечных подмножеств счетного множества счетно.

5.Множество всех подмножеств счетного множества континуально (от лат. continuum – непрерывное) и, в частности, не является счетным.

Несчетное множество – бесконечное множество, которое не является

счетным.

Мощность множества – характеристика множеств, обобщающее понятие количества (числа) элементов конечного множества.

Точная верхняя граница (верхняя грань) и точная нижняя граница

(нижняя грань) – обобщение понятий максимума и минимума множества

соответственно.

Точной (наименьшей) верхней гранью (границей), или супремумом

(лат. supremum – самый высокий) подмножества упорядоченного множества,

называется наименьший элемент, который равен или больше всех элементов

8

множества. Другими словами, супремум – это наименьшая из всех верхних

граней. Обозначается sup X.

Точной (наибольшей) нижней гранью (границей), или инфимумом

(лат. infimum – самый низкий) подмножества упорядоченного множества,

называется наибольший элемент, который равен или меньше всех элементов множества. Другими словами, инфимум – это наибольшая из всех нижних граней. Обозначается inf X.

Пример 10. Для множеств X = [1;3) и Y = (1; 2) (3;5) найти верхнюю и нижнюю границы.

Решение. inf X = 1, sup X = 3 , inf Y = 1, supY = 5 .

1.6 Основные свойства вещественных чисел

I. Сложение и умножение вещественных чисел

Для любой пары a и b вещественных чисел определены и притом единственным образом два вещественных числа a + b и ab , называемые соответственно их суммой и произведением, причем имеют место следующие свойства:

Каковы бы ни были числа a , b и c справедливы следующие соотношения:

1°. a + b = b + a (переместительное свойство).

2°. a + (b + c) = (a + b) + c (сочетательное свойство). 3°. a × b = b × a (переместительное свойство).

4°. a × (b × c) = (a × b)×c (сочетательное свойство).

5°. (a + b)× c = a × c + b × c (распределительное свойство).

6°. Существует единственное число 0 такое, что a + 0 = a для любого

числа a .

7°. Для любого числа а существует такое число (- a), что a + (- a) = 0 . 8°. Существует единственное число 1 ¹ 0 такое, что для любого числа а

имеет место равенство a ×1 = a .

9

9°. Для любого числа a ¹ 0 существует такое число a−1 такое, что

a × a−1 =1. Число a−1 обозначают символом 1 . a

II. Сравнение вещественных чисел

Для любых двух вещественных чисел a и b справедливо одно из отношений: a = b ( a равно b ), a > b ( a больше b ) или b > a .

10°. Если a = b и b = c , то a = c (транзитивность).

Каковы бы ни были числа a , b и c справедливы следующие соотношения:

11°. Если a > b и b > c , то a > c (транзитивность). 12°. Если a > b , то a + c > b + c .

13°. Если a > b и c > 0 , то a × c > b ×c . 14°. Если a > b и c < 0 , то a × c < b × c .

Каковы бы ни были числа a , b , c и d справедливы следующие соотношения:

15°. Если a > b и c > d , то a + c < b + d .

16°. Если a > b и c > d ( a > 0 , b > 0 , c > 0 , d > 0 ), то a × c < b × d . 17°. Если a > b и c < d , то a - c < b - d .

18°. Если a > b > 0 , то 1 < 1 . a b

19°. Если a > b > 0 n Î N , то an > bn .

Эти соотношения называются неравенствами. Неравенства вида a < b и a > b называются строгими неравенствами; неравенства a £ b и a ³ b –

нестрогими.

III. Непрерывность множества вещественных чисел

выполняются неравенства x ≤ c ≤ y .

10