
- •Введение
- •Раздел I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •1. Основные понятия
- •2. Полярная система координат
- •3. Прямая на плоскости. Уравнение прямой с угловым коэффициентом
- •5. Векторное уравнение прямой
- •6. Параметрическое уравнение прямой
- •7. Примеры решения задач по теме «Прямая на плоскости»
- •8. Кривые второго порядка. Эллипс
- •9. Гипербола
- •10. Парабола
- •12. Контрольные работы по разделу «Аналитическая геометрия на плоскости»
- •Раздел II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- •1. Плоскость
- •2. Примеры решения задач по теме «Плоскость»
- •3. Прямая в пространстве
- •4. Примеры решения задач по теме «Прямая в пространстве»
- •5. Поверхности второго порядка
- •7. Контрольная работа для обучающихся по заочной форме по разделу «Аналитическая геометрия»
- •8. Тестовые задания по разделу «Аналитическая геометрия»
- •Темы и задания для самопроверки
- •Требования к экзамену по разделу «Аналитическая геометрия»
- •Библиографический список

Прямые y b x являются асимптотами гиперболы. a
Если центр гиперболы смещен в точку x0, y0 , то уравнение принимает вид
x x0 2 y y0 2 1.
a2 b2
Уравнение вида
|
|
|
|
|
|
|
x x0 2 |
|
|
y y0 2 |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяет гиперболу, ветви которой направлены вверх и вниз: . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число |
|
с |
называется |
|
эксцентриситетом |
гиперболы. |
|||||||||||||||
= |
|
||||||||||||||||||||
Так как |
|
|
|
a |
|
|
|
|
|
|
|
|
И |
|
|
|
|||||
|
|
|
|
|
|
|
|
b 2 |
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
c2 a2 b2 |
|
1 |
Д |
b 2 |
; |
|
1. |
|||||||||||
|
|
|
a2 |
|
|
a2 |
|
|
|
|
, то 1 |
|
|
гип |
|||||||
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
||||||||
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
||||
Чем меньше эксцентр с тет, тем сильнее сжата гипербола по |
|||||||||||||||||||||
вертикали. |
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|||||
Оптическое свойствоигиперболы. Касательная к гиперболе об- |
|||||||||||||||||||||
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
разует равные острые углы с фокальными радиусами и проходит внутри угла. Другими словами, лучи света, исходящие из одного фокуса гиперболы, после зеркального отражения от гиперболы идут так, как если бы они вышли из второго фокуса.
10. Парабола
Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до точки-фокуса равно расстоянию до некоторой фиксированной прямой – директрисы (директриса не проходит через фокус).
29
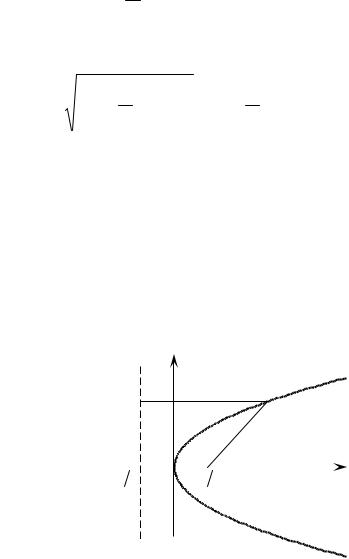
Расстояние от фокуса F до директрисы равно p. Введем систе-
му координат так, чтобы фокус F |
имел координаты |
p |
; 0 |
|
, а урав- |
||
|
|
|
|||||
2 |
|||||||
|
|
|
|
|
|
||
нение директрисы было x p (рис. 14). Получаем уравнение пара- 2
болы
|
|
p 2 |
y |
2 |
x |
p |
. |
|
x |
|
|
|
|||
|
|
2 |
|
|
|
2 |
|
Его можно преобразовать к каноническому уравнению пара- |
|||||||
болы |
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
y2 |
2px. |
|
|
||
|
|
|
|
Д |
|
||
Если p 0, ветви параболы направлены вправо. |
|||||||
Если p 0, ветви направлены влево. |
|
|
|||||
|
б |
y |
|
|
|
||
и |
А |
|
M x, y |
||||
С |
|
|
|||||
p 2 |
|
|
p 2 |
|
x |
||
|
|
|
|||||
|
|
|
|
||||
Рис. 14
Если вершина параболы – точка x0, y0 , то уравнение параболы
y y0 2 2p x x0 .
Уравнение
x2 2py
30
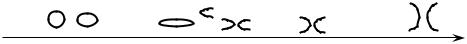
определяет параболу, у которой ветви направлены вверх или вниз. Эксцентриситет параболы пар 1.
Оптическое свойство параболы. Касательная к параболе обра-
зует равные острые углы с фокальным радиусом и лучом, параллельным оси параболы и идущим в сторону ветвей параболы. Другими словами, лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы идут параллельно оси параболы.
Зависимость вида кривой от эксцентриситета
Изобразим, как меняется вид кривой второго порядка в зависимости от экцентриситета (рис. 15).
Окружности |
Эллипсы |
|
Параболы |
Гиперболы |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
||
0 |
|
|
1 |
|
||||
|
|
|
|
|
Рис. 15 |
|
||
|
|
|
|
|
|
|
|
|
11. Примеры решения задач по |
теме «Кривые второго |
|||||||
порядка» |
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
1. Привести к каноническому виду уравнение и построить кри- |
||||||||
вую x2 4x 9y2 |
|
|
А |
|
|
|||
54y 84 0. |
|
|
|
|||||
Решение. Т.к. x |
2 |
2 |
б |
|
|
|
||
|
y |
входят в уравнение с одинаковыми знаками, но |
||||||
|
|
и |
|
|
|
|
|
|
разными коэффициентами, то оно описывает эллипс или особый случай. Сгруппируем слагаемые следующим образом:
|
|
|
|
|
2 |
4x) 9(y |
2 |
6y) 84 0, |
||
|
|
С(x |
|
|||||||
и, |
используя |
известную формулу выделения полного квадрата |
||||||||
|
2 |
|
p 2 |
p 2 |
|
|
||||
x |
|
px x |
|
|
|
|
|
, выделим в выражениях в скобках полные |
||
|
|
|
|
|||||||
|
|
|
2 |
2 |
|
|
||||
квадраты:
(x 2)2 22 9 (y 3)2 32 84 0.
31
После преобразований получим
(x 2)2 9(y 3)2 1
или
(x 2) |
2 |
|
(y 3)2 |
||
|
|
|
|
|
1. |
2 |
|
1 3 |
2 |
||
1 |
|
|
|
|
|
Это уравнение эллипса с центром в точке ( 2,3) и полуосями 1, 1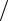 3
3
(рис. 16).
|
|
|
|
|
|
|
И |
|
|
|
|
|
Д |
||
|
|
А |
|
||||
и |
|
Рис. 16 |
|
||||
|
|
|
|
|
|
||
2. Привести к канон ческому виду уравнение 9x2 16y2 144, |
|||||||
С |
|
|
|
|
|
|
|
построить кривую, найтибкоординаты фокусов. |
|||||||
Решение. Разделив обе части уравнения на (–144), получим |
|||||||
|
|
x2 |
y2 |
|
|||
|
|
|
|
|
|
1. |
|
|
4 |
2 |
2 |
|
|||
|
|
|
|
3 |
|
|
|
Очевидно, что это уравнение гиперболы, однако переменные x и y «поменялись ролями» – коэффициент при x2 отрицательный, что
следует учесть при построении линии: фокусы этой гиперболы расположены на оси Oy(рис. 17).
|
Чтобы найти координаты фокусов, воспользуемся |
формулой |
||
связи |
параметров |
гиперболы |
c2 a2 b2 . |
Откуда |
c |
a2 b2 |
|
42 32 |
5, т.е. F(0, 5), |
F (0,5). |
|
|
|
|
1 |
2 |
32

Рис. 17
3. |
Найти проекцию |
фокуса параболы y2 4x на прямую |
|||
: |
x 1 |
|
y 3 |
. |
И |
|
1 |
|
|||
|
2 |
|
Д |
||
Решение. Из уравнения параболы имеем: p 2, т.е. координаты фоку- |
|||||
са F(2,0). Проекция F на |
– точка пересечения и прямой 1, про- |
||||
|
|
А |
|
веденной из F перпендикулярно (рис. 18). |
|
||
|
б |
|
|
и |
|
|
|
С |
|
Рис. 18 |
|
|
|
|
|
Составим уравнение прямой 1, используя критерий перпенди- |
|||
кулярности прямых |
|
|
|
|
1 : 2x y 4 0. |
|
|
Координаты искомой точки x0, y0 пересечения прямых |
и 1 |
||
должны удовлетворять их уравнениям, т.е. x0, y0 – решение системы
33

x0 1 y0 3,2 1
2x0 y0 4 0.
Первое уравнение преобразуется на основании свойства пропорции (произведение средних членов равно произведению крайних) к виду 1(x0 1) 2(y0 3) или x0 2y0 7. Решим полученную систему уравнений
|
|
|
|
|
|
|
2x |
y |
|
|
4 |
, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x0 2y0 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|||||||||
например по формулам Крамера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
1 |
|
5, |
1 |
|
4 |
1 |
|
|
15, |
|
2 |
|
2 |
4 |
|
10, |
|||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
2 |
|
|
|
7 |
2 |
|
|
|
|
1 |
|
7 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
||||
|
|
|
|
|
|
x |
1 |
3, |
y |
0 |
|
2 |
2. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|||||||
Следовательно, проекцией фокуса параболы на прямую является |
||||||||||||||||||||||||||||
точка с координатами |
3, 2 . |
А |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
2 |
9y |
2 |
8x 36y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4. Какую лин ю определяет уравнение 4x |
|
|
|
|||||||||||||||||||||||||
4 0 ? |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
2 |
+9y |
2 |
|
|
говорит о том, |
||||||||
Решение. Наличие в уравнении выражения 4x |
|
|
|
|
|
|||||||||||||||||||||||
что это эллипсСили особый случай. Выделяем полные квадраты по x, y и приводим к каноническому виду
4 x2 2x 9 y2 4y 4 0;
4 x2 2y 1 4 9 y2 4y 4 36 4 0;
4 x 1 2 9 y 2 2 36;
x 1 2 y 2 2 1.
9 4
34
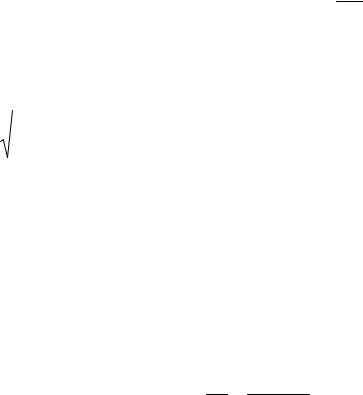
Получили уравнение эллипса с центром 1; 2 , полусями a 3; b 2.
5. Какую линию определяет уравнение 2x2 2y2 8x 5y
4 0?
Решение. Наличие в уравнении выражения 2x2 +2y2 говорит о том, что это окружность или особый случай. Делаем преобразования – выделяем полные квадраты и приводим к каноническому виду
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 x |
|
4x 2 y |
|
|
|
|
|
y |
|
4 0; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
5 |
|
|
|
|
|
25 |
|
|
|
25 |
|
|
|||||||||
|
|
|
|
|
|
2 x |
|
4x 4 8 2 y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
4 0; |
||||||||||
|
|
|
|
|
|
2 |
|
16 |
|
|
8 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
5 |
|
2 |
|
|
|
121 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 x 2 |
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
2 |
|
|
|
121 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x 2 |
y |
|
Д |
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||||||
|
Это уравнен е окружности с центром |
2; |
|
|
|
|
|
, радиусом |
||||||||||||||||||||||||||||
|
4 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
11 |
. |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R |
|
|
121 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6. Какую линию определяет уравнение x2 y2 |
16y 0? |
||||||||||||||||||||||||||||||||||
Решение. Эта Скривая может быть гиперболой или особым случаем. Делаем преобразования
x2 y2 16y 64 64 0;
x2 y 8 2 64;
x2 y 8 2 1. 64 64
35

Это уравнение гиперболы, ветви которой направлены вверхвниз, центр находится в точке 0; 8 , полуоси a b 
 64 8.
64 8.
7. Какую линию определяет уравнение x2 4y2 4x 100 0? Решение. Это эллипс или особый случай. Выделяем полные квадраты
x2 4x 4 4 4y2 100 0;
x 2 2 4y2 96.
Такое равенство невозможно, получили исключительный (осо-
бый) случай – пустое множество точек. |
И |
|
8. Назвать кривую, построить 24x2 |
||
49y2 1176. |
Решение. Для построения кривой приведем ее уравнение к каноническому виду. Для этого разделим обе части равенства на 1176. Имеем
|
x2 |
|
y2 |
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
49 |
|
24 |
1 – каноническое |
уравнение |
|
эллипса |
с |
центом в точке |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|||||||||||||
О(0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Найдем параметры эллипса. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Большая полуось а=7, малая полуось b= |
|
|
|
. Вершины эллипса: |
||||||||||||||||||||||
|
|
|
24 |
|||||||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с a |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|||||||
(7,0), (–7,0), (0, |
24 ), (0, – 24 ); |
|
49 24 5. Фокусы |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|||||
эллипса F1(5,0) и F2(–5,0)б. Эксцентриситет эллипса |
|
(рис. 19). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|||||
|
|
|
-7 |
-5 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 19 |
|
9. Назвать кривую, построить 24x2 49y2 |
1176. |
Решение. Для построения кривой приведем ее уравнение к каноническому виду. Для этого разделим обе части равенства на 1176. Имеем
36
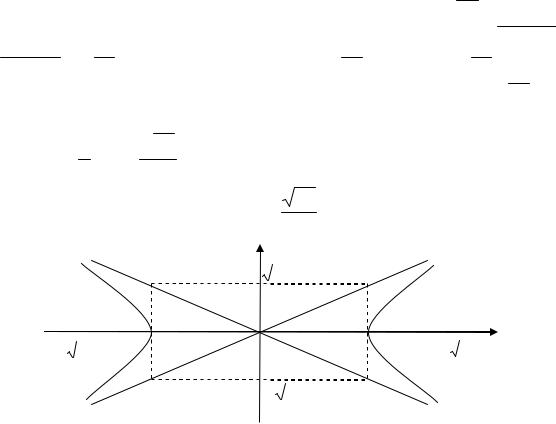
x2 |
y2 |
|||
|
|
|
1 – каноническое уравнение гиперболы с центром в точке |
|
49 |
24 |
|||
|
|
|||
О(0,0).
Найдем параметры гиперболы.
Действительная полуось а=7, мнимая полуось b=
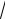 24 . Вершины гиперболы: (7,0), (–7,0). Найдем фокальное расстояние с
24 . Вершины гиперболы: (7,0), (–7,0). Найдем фокальное расстояние с 
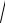 a2 b2
a2 b2
 49 24
49 24 
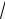 73. Фокусы гиперболы F1(
73. Фокусы гиперболы F1(
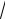 73, 0) и F2 (–
73, 0) и F2 (–
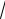 73, 0). Размеры основного прямоугольника гиперболы 2а 2b 14 2
73, 0). Размеры основного прямоугольника гиперболы 2а 2b 14 2
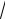 24. Его диагонали лежат на асимптотах гиперболы, определяемых уравнениями y b x
24. Его диагонали лежат на асимптотах гиперболы, определяемых уравнениями y b x 
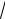 24 x.
24 x.
a |
7 |
Эксцентриситет гиперболы 73 (рис. 20). 7
|
|
|
|
|
|
|
y |
|
|
Д |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
24 |
|
|
|
И F1 |
|||||||||
F2 |
|
|
|
А |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
- |
|
|
|
-7 |
|
|
0 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
73 |
|
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
и |
|
24 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
С |
бРис. 20 |
|
|
|
|
|
|
|
|
|
|||||||||
10. Назвать кривую, построить |
|
|
4x |
2 |
y |
2 |
16x 4y 0. |
||||||||||||||
|
|
|
|
||||||||||||||||||
Решение. Имеем |
общее уравнение кривой 2-го порядка. Так как А=4; |
||||||||||||||||||||
С=1; В=0; A C 0 , то имеем эллипс. |
|
|
|
|
|
|
|
|
|
||||||||||||
Преобразуем уравнение 4(x2 4x) (y2 4y) 0; |
|
|
|
|
|||||||||||||||||
4(x2 2 2x 22) 4 22 (y2 2 2y 22) 22 0; |
|||||||||||||||||||||
|
4(x 2)2 (y 2)2 20; |
(x 2)2 |
|
(y 2)2 |
1 |
||||||||||||||||
|
|
20 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||
– каноническое уравнение эллипса с натным осям и координатами центра перенесем начало координат в точку
осями, параллельными коорди- (–2,2). Для построения кривой (–2,2), т.е. сделаем замену
37

x x x0 x 2;
y y y0 y 2.
В системе координат Ox y уравнение кривой будет иметь кано-
нический вид |
x 2 |
|
y 2 |
1 (рис. 21). |
|
20 |
|||
5 |
|
|
||
|
|
|
|
y |
y
|
|
|
2 |
И |
x |
|
-2 |
-1 |
0 |
x |
|
|
|
|
|
|
|
Для демонстрации |
|
Рис. 21 |
|
|
|
|
|
Д |
|
||
видео нажмите |
|
|
|
||
на ссылку |
https://www.youtube.com/watch?v=wDW5JwrAQlE |
|
|||
|
|
А |
|
|
|
|
|
|
|
||
|
Задачи для самостоятельного решения |
|
|||
|
б |
|
|
|
|
I. Определить вид кривой, построить. Найти экцентриситет (для |
|||||
|
и |
|
|
|
|
эллипсов, гипербол, парабол), координаты фокусов (для эллипсов, ги- |
|||||
пербол, параболС), уравнения асимптот (для гипербол), уравнение директрисы (для парабол):
1)36x2 36y2 36x 24y 23 0;
2)16x2 25y2 32x 50y 359 0;
3) |
1 |
x |
2 |
|
1 |
y |
2 |
x |
2 |
y 1 0 |
; |
4 |
|
9 |
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
4)x2 4y2 4x 8y 8 0;
5)x2 4y2 8y 5 0;
6)x2 y2 6x 100 0;
7)2x2 4x 2y 3 0;
38
8)x2 6x 8 0;
9)x2 2x 5 0;
10)3x2 4y2 6x 8y 0.
II. Написать уравнение
1)кривой, для которой разность квадратов расстояний от каждой точки которой до точек A (– 2, 0) и B (2,0) равна 1;
2)кривой, для которой сумма квадратов расстояний от каждой точки которой до точек A(− 3, 0) и B (3,0) равна 50;
3)окружности с центром в точке M (−1, 2) , проходящей через точку A (2,6);
концами |
|
|
|
|
|
И |
являются |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(4,1) на ок- |
|
ружности |
|
|
|
|
Д |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
||
из них |
|
|
б |
|
|
Определить |
, какие |
|
|
|
|
|
|
|
|||
С |
|
|
|
|
относительно |
кривой |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
второго |
|
|
2 |
2 |
|
|
|
: |
|
1) 6x 2y 20 |
|
8y 5 0; |
|
|
|||
|
и0 и x 4y |
|
|
|
||||
2) 3y 2x 3 0 и 3x2 4y2 6x 8y 0;
3) 4x 5y 39 0 и 36x2 36y2 36x 24y 23 0.
VI.Составить уравнение
1)гиперболы, зная, что угол между асимптотами равен 90° и фокусы находятся в точках с координатами (4; −4) и (−2; −4).
2)эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, дана точка М (5 ; 2) эллипса и его малая полуось b = 3;
3)эллипса, фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная, кроме того, что его малая ось равна 16, а эксцентриситет равен 0,5.
39
