
- •Введение
- •Раздел I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •1. Основные понятия
- •2. Полярная система координат
- •3. Прямая на плоскости. Уравнение прямой с угловым коэффициентом
- •5. Векторное уравнение прямой
- •6. Параметрическое уравнение прямой
- •7. Примеры решения задач по теме «Прямая на плоскости»
- •8. Кривые второго порядка. Эллипс
- •9. Гипербола
- •10. Парабола
- •12. Контрольные работы по разделу «Аналитическая геометрия на плоскости»
- •Раздел II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- •1. Плоскость
- •2. Примеры решения задач по теме «Плоскость»
- •3. Прямая в пространстве
- •4. Примеры решения задач по теме «Прямая в пространстве»
- •5. Поверхности второго порядка
- •7. Контрольная работа для обучающихся по заочной форме по разделу «Аналитическая геометрия»
- •8. Тестовые задания по разделу «Аналитическая геометрия»
- •Темы и задания для самопроверки
- •Требования к экзамену по разделу «Аналитическая геометрия»
- •Библиографический список
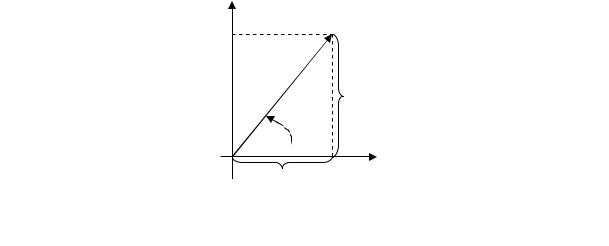
2. Полярная система координат
Полярная система координат – это система координат на плоскости, в которой каждая точка плоскости однозначно определяется двумя числами – полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда связь между точками проще изобразить в виде радиусов и углов. В декартовой прямоугольной системе координат такие соотношения можно получить только применяя тригонометрические уравнения.
Полярная система координат определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Задается также единица масштаба. Любая точ-
ка М на плоскости определяется двумя полярными координатами: по- |
||||
|
|
|
|
И |
лярным радиусом r и полярным углом (рис.2). |
||||
Y |
|
|
Д |
|
|
|
M |
|
|
|
А |
|
||
|
r |
|
y |
|
б |
|
|||
|
X |
|||
и |
|
x |
|
|
O |
|
|
|
|
Рис. 2
ПолярнымСрадиусом r точки M называется расстояние от полюса O до точки M (r = |OM|). Полярным углом называется угол между полярной осью и вектором OM (рис.2). Полярный угол измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Определённая таким образом радиальная координата r может принимать значения от нуля до бесконечности, а угловая координата может быть любой. Обычно полагают 0 ≤ < 2 π
или − π < ≤ π.
Полярные координаты начала координат − точки O: r = 0, угол не определен. У остальных точек r > 0 и угол определен с точностью до 2π.
Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось − с положительной частью оси
8
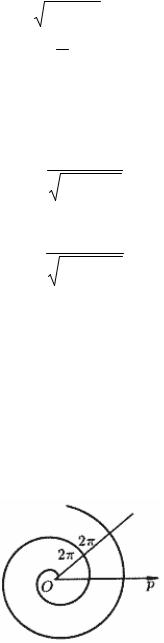
Уравнение Архимедовой спирали в полярной системе координат имеет вид
r = a ,
где a – сдвиг точки M по лучу при обороте на угол, который равен одному радиану.
Обороту прямой на 2π соответствует смещение по лучу на 2aπ – на шаг спирали.
Если мы поворачиваем луч против движения часовой стрелки, получаем правую спираль, если поворачиваем по часовой стрелке – левую спираль.
В природе форму спирали Архимеда имеют большинство раковин. Семена в корзине подсолнечника расположены по спирали. Спираль можно увидеть, например в кактусах, ананасах. Ураган закручивается спиралью. По спирали разбегается стадо оленей. Двойной спиралью закручена молекула ДНК. аже галактики сформированы по
принципу спирали. |
И |
В III веке да нашей эры рхимед на основе своей спирали изо- |
|
видность – винтовой ротор в мясорубке. Шнек используют в меха-
брёл винт, который успешно применяли для передачи воды в ороси- |
|
|
Д |
тельные каналы из водоёмов, расположенных ниже. Позже на основе |
|
А |
|
б |
|
винта Архимеда создалиишнек («улитку»). Его очень известная разно-
низмах для перемеш ван я материалов различной консистенции. В технике нашлиСпр менен е антенны в виде спирали Архимеда. Само-
центрирующийся патрон выполнен по спирали Архимеда. Звуковые дорожки на CD и DVD дисках также имеют форму спирали Архимеда.
3. Прямая на плоскости. Уравнение прямой с угловым коэффициентом
На плоскости прямая чаще всего задается уравнениями вида:
1)y kx b – уравнение прямой с угловым коэффициентом (для прямых, не параллельных оси Oy);
2)Ax By C 0 общее уравнение прямой;
10

3)r r0 аt векторное уравнение;
4)x x0 lt; параметрическое уравнение прямой.
y y0 mt.
Уравнение прямой с угловым коэффициентом
Тангенс угла наклона прямой к положительному направлению оси Ox будем называть угловым коэффициентом этой прямой
|
|
k = tg . |
|
|
|
Возможны следующие случаи положения прямых в зависимости |
|||||
от k (рис. 4) |
|
|
И |
||
|
|
|
|
||
|
|
|
|
|
|
|
k 0 |
|
Д |
||
|
|
|
k 0 |
|
|
|
|
А |
|
|
|
|
б |
|
|
|
|
|
и |
|
|
|
|
|
С |
|
|
k |
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
Рис. 4
Вывод уравнения прямой
Пусть известны координаты двух точек M0 x0, y0 и M1 x1, y1
11

на прямой (рис. 5). Из рисунка 5 очевидно, что k y1 y0 . x1 x0
y |
|
|
y1 |
|
M1 |
y0 |
M0 |
|
|
|
|
0 x0 x1 x
|
|
|
|
Рис. 5 |
И |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
Д |
и коор- |
||
|
Пусть теперь известен угловой коэффициент прямой k |
|||||||
динаты точки M0 x0, y0 |
на прямой. Пусть M x,y произвольная |
|||||||
точка на прямой. |
|
А |
|
|
||||
|
Тогда |
|
|
|
||||
|
б |
|
|
|||||
|
|
|
|
|||||
|
|
|
k |
|
y y0 |
|
|
|
или |
и |
x x0 |
|
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
С |
|
|
|
|
|
|
|
|
|
y y0 k x x0 |
|
|
|||||
|
|
|
|
|||||
это уравнение прямой, проходящей через точку M0 x0, y0 .
Раскроем скобки
y kx y0 kx0.
Теперь обозначим b y0 kx0 , тогда получим
ykx b
это уравнение прямой с угловым коэффициентом.
Число b называется свободным членом.
12
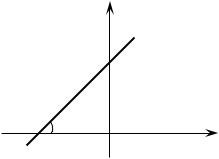
Геометрически число b равно отрезку, отсекаемому прямой на оси Oy(рис. 6).
y
b
x
Рис. 6
Уравнение прямой, проходящей через две заданные точки
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
M1 x1, y1 , ле- |
|||||
|
Пусть известны координаты точек |
M0 |
x0, y0 и |
||||||||||||||||
жащих на прямой. Так как k |
y y0 |
и |
k |
y1 |
y0 |
, то, приравнивая |
|||||||||||||
|
|
|
|
|
x x |
0 |
|
|
|
Иx x |
|
||||||||
выражения, получаем уравнение |
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
б |
|
y1 |
y0 |
|
|
|
|
|
|
|||||||||
|
|
|
y y0 |
|
|
|
|
|
|
|
|
|
|||||||
|
и |
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|||
|
|
|
x x |
|
|
|
0 |
|
|
|
|
|
|
|
|||||
или |
|
|
|
А0 1 |
|
|
|
|
|
|
|
||||||||
|
|
y y0 |
|
|
|
x x0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
y1 y0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x1 |
x0 |
|
|
|
|
|
||||||||
Пример.Составить уравнение прямой, проходящей через точки
M0 2, 3 и M1 1, 1 .
Решение. Подставляем координаты точек в уравнение и делаем преобразования
|
y 3 |
|
|
x |
2 |
; |
|||
1 3 |
|
|
|
||||||
1 |
2 |
||||||||
|
y 3 |
|
x 2 |
; |
|||||
|
|
|
|||||||
|
4 |
|
|
1 |
|||||
1 y 3 4 x 2 .
13
После упрощений получаем уравнение прямой в виде с угловым коэффициентом y 4x 5.
Угол между прямыми
Даны уравнения двух прямых
1 : y k1 x b1;
2 : y k2 x b2 .
|
|
|
|
|
|
|
|
. |
||
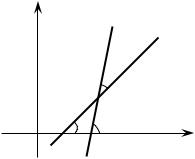
Найдем угол между прямыми 1, 2 |
||||||||||
Из рисунка 7 получаем, что 2 |
И |
|||||||||
1. |
|
|
|
|||||||
|
y |
|
|
Д |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
А |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
|
|
|
|
бРис.7 |
|
|
|
|
|
||||
Используем тригонометрическуюи |
формулу |
|
|
|||||||
tg tg |
|
|
|
tg 2 tg 1 |
. |
|||||
|
|
|
|
|
|
|||||
С |
|
2 |
1 |
1 tg tg |
2 |
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
Так как, по определению углового коэффициента, tg =k, то
|
|
|
|
k2 k1 |
|
|
||
tg |
, |
2 |
= |
|
|
. |
||
|
|
|||||||
1 |
|
|
1+k k |
2 |
|
|
||
|
|
|
|
1 |
|
|
||
Это формула для нахождении угла между прямыми.
Наличие модуля в формуле позволяет находить сразу острый угол между прямыми.
14
Следствием этой формулы являются условия параллельности и перпендикулярности прямых.
Условие параллельности прямых
|
|
|
|
|
|
|
|
|
|
|
|
1 || 2 k1 k2 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
если |
|
1 |
|| 2 , |
то 1 2 |
0, |
tg = 0. |
То есть |
||||||||||||||||||||
|
|
|
|
k2 k1 |
|
= 0 k = k |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
tg |
, |
2 |
= |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
1+k k |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Условие перпендикулярности прямых |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 k1 k |
|
И |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
||||
|
Действительно, |
если |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 900 |
, tg900 |
не суще- |
|||||||||||
|
|
|
|
|
, то = |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
А |
1 |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
ствует. |
То есть |
|
|
|
|
|
|
k2 k1 |
|
|
не существует |
знаменатель |
|||||||||||||||||
tg , = |
б |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
1+k k |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
дроби не определен k1k2 |
|
= – 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
4. Общее уравнен е прямой |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By C 0 (где |
|||||||
|
Всякое уравнен е первой степени вида |
||||||||||||||||||||||||||||
A,B,C – постоянные, причем A B |
|
0), определяет на плоскости |
|||||||||||||||||||||||||||
прямую. Это уравнение называется общим уравнением прямой.
Частные случаи
1. Прямая, определяемая уравнением Ax By 0 (С = 0, уравнение можно преобразовать к виду y kx), проходит через начало координат.
2.Прямая, определяемая уравнением y b (А = 0), параллельна оси Ох. Прямая, определяемая уравнением y 0 это ось Ох.
3.Прямая, определяемая уравнением x a (В = 0), параллельна оси Оу. Прямая вида x 0 это ось Оу.
15
