
- •Введение
- •Раздел I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •1. Основные понятия
- •2. Полярная система координат
- •3. Прямая на плоскости. Уравнение прямой с угловым коэффициентом
- •5. Векторное уравнение прямой
- •6. Параметрическое уравнение прямой
- •7. Примеры решения задач по теме «Прямая на плоскости»
- •8. Кривые второго порядка. Эллипс
- •9. Гипербола
- •10. Парабола
- •12. Контрольные работы по разделу «Аналитическая геометрия на плоскости»
- •Раздел II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- •1. Плоскость
- •2. Примеры решения задач по теме «Плоскость»
- •3. Прямая в пространстве
- •4. Примеры решения задач по теме «Прямая в пространстве»
- •5. Поверхности второго порядка
- •7. Контрольная работа для обучающихся по заочной форме по разделу «Аналитическая геометрия»
- •8. Тестовые задания по разделу «Аналитическая геометрия»
- •Темы и задания для самопроверки
- •Требования к экзамену по разделу «Аналитическая геометрия»
- •Библиографический список

4.Если A 0; B 0; C 0, то уравнение можно преобразовать
квиду уравнения прямой «в отрезках»
x y 1. a b
Числа a,b – это отрезки, отсекаемые прямой на координатных осях (рис. 8).
y
|
|
b |
|
Рис. 4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a |
И |
|||||
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
Д |
||||||
|
|
|
|
Рис. 8 |
|
|
|
|
|
|
|||
|
|
А |
|
|
|
|
|
|
|||||
Расстояние от точки до прямой |
|||||||||||||
Рассмотрим прямую Ax By C 0 |
и точку M0 x0, y0 (рис. 9). |
||||||||||||
Расстояние от точки до прямой находят по формуле |
|||||||||||||
|
бd |
|
Ax0 By0 C |
|
|
. |
|||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
A2 B2 |
|
|
||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
d |
|
M0 x0, y0 |
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Ax+By+C=0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9
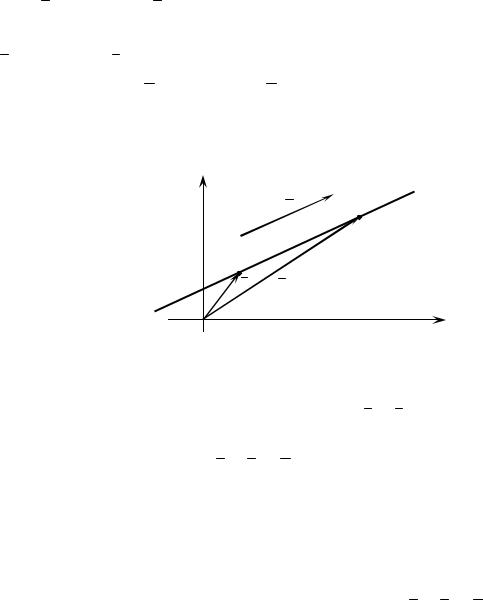
5. Векторное уравнение прямой
Рассмотрим прямую и вектор a , m 0, параллельный прямой. Всякий такой вектор называется направляющим.
16
|
Пусть на прямой даны две точки: M0 x0, y0 |
|
и M x,y . Тогда |
||||||||||||||||||||||||||||||||
векторы |
r0 |
|
|
0 и |
|
r |
|
|
|
|
|
называются радиус-векторами точек |
|||||||||||||||||||||||
OM |
|
OM |
|||||||||||||||||||||||||||||||||
M0 , M . Координаты радиус-векторов совпадают с координатами то- |
|||||||||||||||||||||||||||||||||||
чек: |
r0 x0, y0 ; |
r |
x, y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Так как |
M0M |
|| |
a |
, то |
M0M |
|
|
a |
|
t, где t |
|
– некоторое число (па- |
||||||||||||||||||||||
раметр). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0(x0,y0) |
|
|
|
|
|
|
|
|
|
|
a |
|
M(x, y) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
r |
|
И |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r0 |
M0M (рис. 10). |
|||||||||||||||
|
Используем правило сложения векторов |
|
|
|
|||||||||||||||||||||||||||||||
|
Получим |
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
и |
|
r |
|
r0 |
|
at. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Это и есть векторное уравнение прямой.
6. Параметрическое уравнение прямой |
|
Запишем теперь векторное уравнение прямой r r0 at в коор- |
|
динатах |
С |
x, y x0, y0 ,m t .
Выпишем равенства для каждой из координат, получим
x x0 t;
y y0 mt.
Это параметрическое уравнение прямой.
17
Здесь x0, y0 – координаты точки на прямой, ,m – координаты направляющего вектора.
7. Примеры решения задач по теме «Прямая на плоскости»
|
|
|
1. Написать уравнения прямых, |
проходящих |
через |
точку |
||||||||||||||||||||||||||||
M0 2, 1 параллельно, |
перпендикулярно и под углом |
45 |
к прямой |
|||||||||||||||||||||||||||||||
y 2x 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Для решения задачи используем уравнением прямой, про- |
||||||||||||||||||||||||||||||||||
ходящей через заданную точку |
|
y y0 |
k x x0 |
. Подставим в это |
||||||||||||||||||||||||||||||
уравнение |
координаты |
|
точки |
|
|
M0 |
2, |
(1 |
− |
), получим уравнение |
||||||||||||||||||||||||
y 1 k x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Определим теперь угловой коэффициент k прямой. По условию |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
используя критерий |
|||||||||||
прямая параллельна прямой y 2x 4, |
поэтому, |
|||||||||||||||||||||||||||||||||
параллельности прямых, находим, что k 2. Подставляем в уравне- |
||||||||||||||||||||||||||||||||||
ние: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|||||||||
y 1 2x 4 2x 4 y 1 0 2x y 5 = 0 – нашли урав- |
||||||||||||||||||||||||||||||||||
нение прямой, параллельной данной. |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Если искомая прямая перпендикулярна данной, то, из критерия |
|||||||||||||||||||||||||||||||
ортогональности |
прямых |
|
|
|
|
|
k |
k |
|
1, |
находим |
k |
1 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2и |
|
2 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
Подставим найденное значен е k |
1 |
|
в уравнение y 1 k x 2 , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
получим |
y 1 |
1 |
x |
2 x 2 2y 2 0 x 2y 0 |
– это |
|||||||||||||||||||||||||||||
уравнение прямой, перпендикулярной прямой y 2x 4. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
Определим далее угловой коэффициент прямой, проходящей |
|||||||||||||||||||||||||||||||
под |
углом |
|
45 |
к |
данной |
прямой |
|
y 2x 4, |
по |
формуле |
||||||||||||||||||||||||
|
|
|
k2 k1 |
|
. |
Подставляя |
|
в |
|
эту |
|
формулу |
= 45 , |
получим |
||||||||||||||||||||
tg |
|
|
|
|
|
|||||||||||||||||||||||||||||
1 k1k2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 k1 |
|
(так как угловой коэффициент данной прямой k 2). |
||||||||||||||||||||||||||||||
1 |
|
|
|
|||||||||||||||||||||||||||||||
1 2k1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
18
Имеем |
1 2k |
2 k |
k |
|
1 |
или k 3. И тогда |
|
||||||
|
1 |
1 |
1 |
3 |
1 |
|
y 3x 5 0 |
и 3y x 5 0 |
– уравнения прямых, проходящих под |
||||
углом 45 к данной. |
|
|
|
|
|
|
2. Найти уравнение прямой, проходящей через точки A1 5, 1 и |
||||||
A2 2,5 .
Решение. Воспользуемся уравнением прямой, проходящей через две
точки |
y y0 |
|
x x0 |
: |
y1 y0 |
|
|||
|
|
x1 x0 |
||
x 5 |
|
y 1 |
|
x 5 |
|
y 1 |
2 x 5 y 1 2 x 10 y 1 0 |
|
|
|
|
|
|||||
2 5 |
|
5 1 |
|
3 |
6 |
|
И |
|
|
|
|
|
|||||
2 x y 9 0. |
|
|
|
Д |
||||
|
3. Найти угол между прямыми: |
|||||||
|
y 3x и y 2 x 5. |
|||||||
Решение. Для вычисления угла между прямыми используем формулу |
||||||||||||||||||||
|
|
k |
2 k1 |
|
|
|
|
|
А |
|
|
3 2 |
|
|
|
5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
tg |
|
|
. Так как k |
3; k |
2 |
2, то tg |
|
|
|
|
|
1. От- |
||||||||
|
|
|
|
|
|
|||||||||||||||
|
1 k1k2 |
|
|
|
1 |
|
|
|
|
|
1 6 |
|
|
5 |
|
|||||
|
|
|
1 |
б |
|
|
|
|
|
|
||||||||||
сюда arctg 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
45 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
|
|
|
4 |
|
|
|
|
|
АВС: |
A(3,1), B(1,7),С(6,3). |
|||||||||
Заданы верш ны |
треугольника |
|||||||||||||||||||
Требуется: |
|
|
|
|
|
|
|
|
АВС; |
|
|
|
|
|
|
|
||||
1) |
составить уравнен |
я всех сторон |
|
|
|
|
|
|
|
|||||||||||
2) |
уравнение высоты, опущенной из вершины В на сторону АС; |
|||||||||||||||||||
3) |
уравнение медианы, проведенной из вершины С; |
|
|
|
||||||||||||||||
4) |
расстояние от вершины С до стороны АВ; |
|
|
|
|
|
|
|
||||||||||||
5) |
найти Сугол между сторонами АС и АВ; |
|
|
|
|
|
|
|
||||||||||||
6) |
вычислить периметр треугольника АВС. |
|
|
|
|
|
|
|
||||||||||||
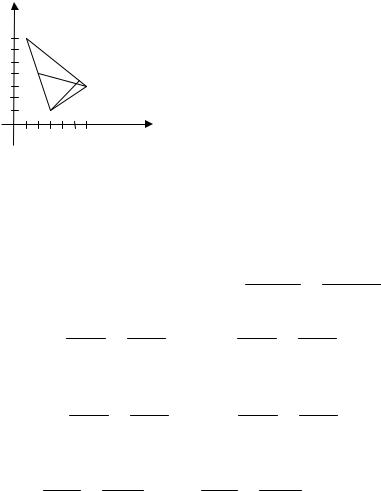
Решение. Построим в декартовой системе координат треугольник АВС с заданными координатами вершин (рис. 11).
19
y
B
H
M
C
A
o x
Рис. 11
1) Для нахождения уравнения сторон треугольника воспользуем-
x x |
y y |
4x 5y 39 0. ибАДИ
2)Пусть АНС– высота, опущенная из вершины А на сторону ВС. Найдем ее уравнение в виде y y0 k x x0 . Так как высота опуще-1 .-1ся уравнением прямой, проходящей через две точки
сти прямых |
1 |
|
2 |
k |
k |
2 |
1. Найдем, что |
x 1 |
|
y 7 |
– уравне- |
|
|
|
|
||||||||||
|
|
1 |
|
|
4 |
|
5 |
|||||
|
|
|
|
|
|
|
|
|
||||
ние высоты АН.
3) Пусть АМ – медиана, проведенная из вершины С на сторону АВ. По определению медианы, точка М делит отрезок АВ пополам. Координаты середины отрезка находим по формулам
20
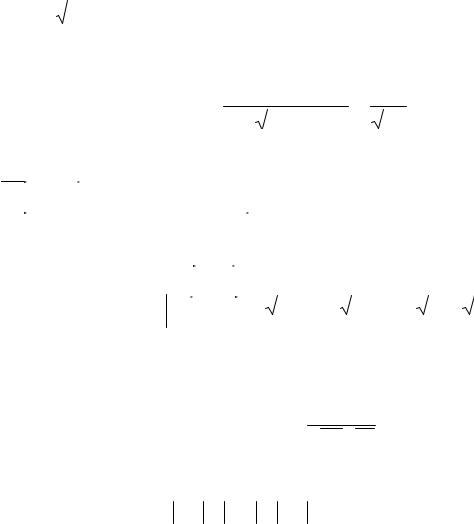
|
|
|
|
|
|
|
|
|
|
|
xM |
= |
|
xA + xB |
|
|
= |
3+1 |
= 2; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
yM |
= |
|
|
yA + yB |
|
= |
|
1+7 |
= 4. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для нахождения уравнения медианы СМ воспользуемся уравне- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
нием прямой, проходящей через две точки: |
|
|
|
x x1 |
|
y y1 |
. Так как |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
y2 y1 |
||||||||||||||
С(6,3), |
M(2,4), то |
x 6 |
|
|
y 3 |
|
или |
|
|
x 6 |
|
|
|
y 3 |
– уравнение медиа- |
||||||||||||||||||||||||||||||||||||||||
2 6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ны СМ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
4) Расстояние от вершины С до стороны |
|
АВ |
находим по формуле |
|||||||||||||||||||||||||||||||||||||||||||||||||
d |
|
|
Ax0 |
By0 C |
|
|
. Так как 6x 2y 20 0– общее уравнение сторо- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ны АВ, |
то А=6; В=2; С= –20; x0 |
|
xC |
6; y0 |
|
yC 3. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 6 2 3 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
d |
Д |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 4 |
40 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
АВ и |
АС равен углу между векторами |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
5) Угол между сторонами |
||||||||||||||||||||||||||||||||||||||||||||||||||||
AB и AC. Для точек A(3,1), B(1,7),С(6,3) имеем |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
AB 1 3;7 1 2;6 , |
AC 6 3;3 1 3;2 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
cos |
AB |
|
AC |
|
|
|
|
|
2 3 6 2 |
|
|
|
|
|
|
6 |
|
|
|
. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
С |
|
AC |
|
|
|
|
|
|
|
|
4 36 9 4 |
|
|
|
40 13 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Искомый угол между сторонами АВ и АС будет равен
arccos 6 . 
 40
40
 13
13
6) Для вычисления периметра треугольника АВС сложим длины всех его сторон Р АВ АС ВС .
21

Так как AB 2;6 , AC 3;2 , ВC 5; 4 ,
то АВ 
 4 36
4 36 
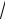 40,
40,
АС 
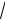 9 4
9 4 
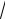 13; ВС
13; ВС 
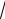 25 16
25 16 
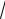 41.
41.
Итак, периметр треугольника Р 
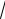 40
40 
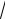 13
13 
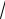 41.
41.
Задачи для самостоятельного решения
I. Даны координаты точек A1, A2 и A3:
1. A 7;3 , |
|
, |
|
6. |
A 7; 4 ,A 3; 7 , |
|
||
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
Д |
|
||
|
|
|
|
А |
|
|
||
|
|
С |
б |
|
|
|
|
|
1) |
|
|
|
|
|
|
||
найти длинуиотрезка A1A2; |
|
|
A2 A3, A1A3, записать в об- |
|||||
2) |
составить уравнения прямых A1A2, |
|||||||
щем виде |
|
|
|
|
|
|
|
|
3) |
нарисовать прямые A1A2, A2 A3, A1A3; |
|
||||||
4) |
составить уравнение прямой, проходящей через точку A3 |
па- |
||||||
раллельно прямой A1A2 ; |
|
|
|
|
A3 |
|||
5) |
составить уравнение прямой, проходящей через точку |
|||||||
перпендикулярно прямой A1A2 ; |
|
|
|
|
||||
6) |
составить уравнение прямой, |
проходящей под углом = 45 |
||||||
к прямой A2 A3; |
|
|
|
|
|
|
||
7) |
составить уравнение прямой, |
проходящей под углом = 30 |
||||||
к прямой A2 A3; |
|
|
|
|
|
|
||
22
8)найти расстояние от точки A3 до прямой A1A2 ;
9)определить угол между прямыми A1A2 и A2 A3;
10)определить длины всех сторон и все углы в треугольнике
A1A2 A3. |
|
|
|
|
II. |
Заданы вершины треугольника |
АВС: A(3,1), B(1,7),С(6,3). |
||
Требуется: |
|
|
|
|
1) |
составить уравнения прямых – всех сторон АВС; |
|||
2) |
уравнение прямой – высоты, опущенной из вершины В на |
|||
сторону АС; |
|
|
|
|
3) |
уравнение прямой– медианы, проведенной из вершины С; |
|||
4) |
расстояние от вершины С до стороны АВ; |
|||
5) |
найти угол между сторонами АС и АВ; |
|||
6) |
вычислить периметр треугольника АВС. |
|||
1) |
равноудалены от точек A (0, 2) и B (4, 2); |
|||
2) |
втрое дальше от точки A (0, 9), чем от точки B (0, 1); |
|||
3) |
вдвое ближе к точке A (1, 1), чем к точке B (4, 4). |
|||
IV. Записать уравнение |
А |
И |
||
|
||||
1) |
биссектрисы второго и четвертого координатных углов; |
|||
2) |
|
б |
|
|
геометрического места точекД, равноудаленных от точки A |
||||
(2,2) и |
линии, каждая точка которой вдвое дальше от оси Ox , чем от |
|||
3) |
||||
оси Oy; |
|
|
|
|
4) |
геометрического места точек, равноудаленных от точки |
|||
A(4,0) и от оси Oy; |
|
|
|
|
5) |
геометрическогоиместа точек, равноудаленных от точки A |
|||
(4,2) и от начала координат; |
|
|
||
6) |
линии, все точки которой вдвое ближе к точке A (0, 1) , чем к |
|||
точке B (0, 4). С |
|
|
|
|
V. Установить, какие линии определяются следующими уравне- |
||||
ниями |
х = |у |; |
|
|
|
1) |
|
|
|
|
2) y + |x|=0; |
|
|
|
|
3) |
х + |у |= 0; |
|
|
|
4) |
у = |х − 1|; |
|
|
|
5) y = |x + 2|; |
|
|
|
|
6) |
у = − |х − 5|. |
|
|
|
VI. Заданы две противоположные вершины квадрата A и С . Требуется найти остальные вершины и уравнения сторон квадрата.
23

1)А (2, – 2), С (16, 0);
2)А (–1, 7), С (13, 9);
3)А (1, 1), С (15, 3);
4)А (–8, 3), С (6, 5);
5)А (2, –4), С (16, –2);
6)А (3, 3), С (17, 5);
7)А (–6, 2), С (8, 4);
8)А (2, –8), С (16, –6);
9)А (– 4, 1), С (10, 3);
10)А (3, 4), С (17, 6).
Ответы: I. 1.
1) 13;
2) y 5 x 1 – уравнение прямой A1A2 в виде с угловым ко-
|
|
|
|
12 |
|
|
|
12 |
|
|
Д |
|
|
|
|
|||||||||||||||
эффициентом; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5 |
|
|
|
|
49 |
|
|
|
|
И |
|
|
|
|
||||||||||||||||
4) |
y |
|
x |
|
; |
А |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
12 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5) y |
12 |
|
|
x 14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
|
x 3 y 1 |
– уравнен е прямой АВ; |
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
22С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
x 1 |
|
y 7 |
|
– уравнен е высоты АН; |
|
|
|
|
||||||||||||||||||||
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3) |
|
x 6 |
|
|
y 3 |
– уравнение медианы; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) d |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5) угол между сторонами АВ и АС равен arccos |
|
|
|
|
; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
6) периметр треугольника Р |
|
|
40 |
|
13 |
|
||||||||||||||||||||||||
40 |
|
13 |
|
41 |
. |
|
|
|
|
|||||||||||||||||||||
24
