
2471
.pdf
РАСЧЕТ СИСТЕМ И МЕХАНИЗМОВ
ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ
МАТЕМАТИЧЕСКИМИ МЕТОДАМИ
b
A F(x)dx
a
Омск 2011
103
Министерство образования и науки РФ ГОУ ВПО «Сибирская государственная автомобильно-дорожная
академия (СибАДИ)»
РАСЧЕТ СИСТЕМ И МЕХАНИЗМОВ
ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ
МАТЕМАТИЧЕСКИМИ МЕТОДАМИ
Учебное пособие
Под редакцией Ю.П. Макушева
Омск
СибАДИ
2011
104
УДК 621.43, 51-7 ББК 31.365.22.11
М 17
Авторы: Ю.П. Макушев, Т.А. Полякова, Л.Ю. Михайлова, А.В. Филатов
Рецензенты:
д-р техн. наук, проф. В.В. Шалай (ОмГТУ); д-р техн. наук, проф. А.И. Володин (ОмГУПС);
канд. физ.-мат. наук, ст. пр. Т.А. Щербинина (ОмГТУ)
Работа одобрена редакционно-издательским советом академии в качестве учебного пособия при изучении дисциплин «Динамика двигателей», «Системы двигателей» для студентов специальности «Двигатели внутреннего сгорания».
Учебное пособие одобрено кафедрой «Высшая математика» СибАДИ и рекомендуется для студентов технических специальностей вузов.
М 17 Расчет систем и механизмов двигателей внутреннего сгорания мате-
матическими методами: учебное пособие / Ю.П. Макушев, Т.А. Полякова, Л.Ю. Михайлова и др.; под ред. Ю.П. Макушева. Омск: СибАДИ, 2011. 284 с.
Учебное пособие состоит из двух частей. В первой части приведены основы дифференциального и интегрального исчисления функции одной действительной переменной. Дано понятие производной как скорости изменения процесса, приведены примеры расчетов. Рассмотрены дифференциальные уравнения и показано их применение при решении технических задач.
Во второй части учебного пособия содержатся расчеты систем двигателей с применением интегральных и дифференциальных уравнений.
Типовые задачи, их пояснение и решение с использованием интегрального и дифференциального исчисления могут быть полезны студентам младших курсов, изучающих математику. Связь со специальными дисциплинами повышает интерес к математике. На старших курсах, полученные знания по дисциплине «Высшая математика», становятся прикладными при изучении дисциплин «Теоретическая механика», «Механика жидкости и газа», «Термодинамика», «Теория рабочих процессов в двигателях внутреннего сгорания», «Динамика двигателей», «Системы двигателей», «Агрегаты наддува двигателей».
Каждая глава завершается перечнем вопросов для самоконтроля, что позволяет читателю проверить степень усвоения изучаемого материала.
Учебное пособие предназначено для студентов специальности 140501 «Двигатели внутреннего сгорания», 190601 «Автомобили и автомобильное хозяйство» и может быть полезно для студентов других технических специальностей, а также инженерам и аспирантам.
Табл. 22. Ил. 97. Прил. 3. Библиогр.: 43 назв.
ГОУ «СибАДИ», 2011
105
ОГЛАВЛЕНИЕ |
|
Введение............................................................................................................. |
6 |
1. Основы дифференциального исчисления функции одной действи- |
|
тельной переменной ......................................................................................... |
9 |
1.1. Понятие производной функции ................................................................. |
9 |
1.1.1. Физический и геометрический смысл производной.............................. |
17 |
1.1.2. Основные правила дифференцирования................................................. |
31 |
1.1.3 Производная сложной функции............................................................... |
32 |
1.1.4. Производная обратной функции............................................................. |
33 |
1.1.5. Производная неявно заданной функции................................................. |
35 |
1.1.6. Производные функций, заданных параметрически ............................... |
37 |
1.2. Производные высших порядков................................................................. |
38 |
1.2.1. Производные высших порядков явно заданной функции...................... |
38 |
1.2.2. Производные высших порядков неявно заданной функции.................. |
41 |
1.2.3. Производные высших порядков функций, заданных параметрически. |
42 |
1.3. Дифференциал ............................................................................................ |
44 |
1.3.1. Геометрический и механический смысл дифференциала...................... |
48 |
1.3.2. Свойства дифференциала........................................................................ |
49 |
1.3.3. Дифференциал сложной функции........................................................... |
50 |
1.3.4. Дифференциалы высших порядков......................................................... |
51 |
2. Основы интегрального исчисления функции одной действительной |
|
переменной......................................................................................................... |
53 |
2.1. Неопределенный интеграл ......................................................................... |
54 |
2.2. Определенный интеграл............................................................................. |
60 |
2.2.1. Свойства определенного интеграла........................................................ |
61 |
2.2.2. Вычисление определенного интеграла................................................... |
62 |
2.3. Приложения определенного интеграла ..................................................... |
64 |
2.3.1. Физические приложения определенного интеграла............................... |
65 |
2.3.2. Геометрические приложения определенного интеграла........................ |
71 |
3. Дифференциальные уравнения .................................................................. |
80 |
3.1. Понятие дифференциального уравнения................................................... |
80 |
3.2. Дифференциальные уравнения первого порядка...................................... |
83 |
3.2.1. Дифференциальные уравнения с разделяющимися переменными ....... |
84 |
3.2.2. Линейные дифференциальные уравнения первого порядка.................. |
86 |
3.3. Дифференциальные уравнения высших порядков (линейные диффе- |
|
ренциальные уравнения высших порядков с постоянными коэффициента- |
|
ми) ...................................................................................................................... |
90 |
3.3.1. Линейные однородные дифференциальные уравнения n-го порядка с |
|
постоянными коэффициентами ........................................................................ |
91 |
3.3.2. Линейные неоднородные дифференциальные уравнения n-го поряд- |
|
ка с постоянными коэффициентами................................................................. |
94 |
4. Определение скорости и ускорения поршня с помощью |
|
производных...................................................................................................... |
103 |
4.1. Определение пути поршня......................................................................... |
104 |
106
4.2. Определение скорости поршня.................................................................. |
106 |
4.3. Определение ускорения поршня................................................................ |
108 |
4.4. Приближенные вычисления пути, скорости и ускорения поршня........... |
112 |
5. Расчетное и экспериментальное определение давления в цилиндре и |
|
диагностика двигателя по индикаторной диаграмме ................................. |
115 |
5.1. Основные термины и определения............................................................ |
115 |
5.2. Общее устройство и принцип работы двигателя внутреннего сгора- |
|
ния...................................................................................................................... |
116 |
5.2.1. Четырехтактный рабочий цикл............................................................... |
118 |
5.2.2. Индикаторная диаграмма двигателя....................................................... |
119 |
5.3. Методика построения индикаторной диаграммы и определение поло- |
|
жительной работы при помощи интегрирования............................................. |
120 |
5.4. Экспериментальное определение давления газов в цилиндре двигателя |
128 |
5.5. Диагностика двигателя по анализу индикаторной диаграммы ................ |
130 |
5.6. Расчет процесса сгорания топлива............................................................. |
131 |
6. Определение момента инерции элементов коленчатого вала................ |
135 |
6.1. Расчетно-экспериментальное определение момента инерции части ко- |
|
ленчатого вала ................................................................................................... |
136 |
6.2. Расчетное определение момента инерции элементов коленчатого вала.137 |
|
7. Определение момента инерции маховика................................................. |
141 |
7.1. Расчетно-экспериментальное определение момента инерции маховика.142 |
|
7.2. Расчетное определение момента инерции маховика ................................ |
143 |
8. Расчет маховика............................................................................................ |
145 |
8.1. Определение момента инерции маховика по результатам динамиче- |
|
ского расчета двигателя .................................................................................... |
145 |
8.2. Пример расчета маховика........................................................................... |
150 |
9. Расчет коленчатого вала двигателя на крутильные колебания............ |
152 |
9.1. Свободные крутильные колебания вала с одной массой.......................... |
152 |
9.2. Вынужденные крутильные колебания вала с одной массой .................... |
156 |
9.3. Последовательность расчета коленчатого вала на крутильные колебания... |
158 |
9.3.1. Приведение крутильной системы вала................................................... |
159 |
9.3.2. Определение частоты собственных крутильных колебаний приве- |
|
денной системы ................................................................................................. |
160 |
9.3.3. Определение резонансной критической частоты вращения.................. |
161 |
9.3.4. Выработка рекомендаций, устраняющих крутильные колебания......... |
163 |
10. Методика построения дифференциальной и интегральной характе- |
|
ристик подачи топлива.................................................................................... |
165 |
10.1. Расчет цикловой подачи топлива и выбор эффективного проходного |
|
сечения распылителя......................................................................................... |
165 |
10.2. Методика построения дифференциальной характеристики подачи то- |
|
плива................................................................................................................... |
167 |
10.3. Расчет при помощи современной вычислительной техники диффе- |
|
ренциальной характеристики впрыскивания................................................... |
172 |
10.4. Формы дифференциальной характеристики впрыскивания................... |
173 |
10.5. Построение интегральной характеристики впрыскивания..................... |
177 |
107
11. Расчет параметров струи дизельного топлива ....................................... |
179 |
11.1. Расчет мелкости распыливания жидкого топлива................................... |
179 |
11.2. Определение формы распыленного топливного факела при впрыске в |
|
неподвижную среду........................................................................................... |
186 |
12. Расчет центробежного компрессора и центростремительной |
|
турбины.............................................................................................................. |
190 |
12.1. Методика расчёта центробежного компрессора с радиальными ло- |
|
патками............................................................................................................... |
190 |
12.2. Расчёт радиально-осевой турбины........................................................... |
199 |
13. Основы расчета и выбора теплообменных аппаратов.......................... |
208 |
13.1. Основные формулы, используемые при расчете теплообменных ап- |
|
паратов............................................................................................................... |
208 |
13.2. Выбор основных параметров теплообменника типа «труба в трубе».... |
213 |
13.3. Пример расчета теплообменного аппарата типа «труба в трубе».......... |
217 |
14. Гидравлический расчет трубопроводов и насосной установки........... |
221 |
14.1. Основные расчетные формулы ................................................................ |
221 |
14.2. Насосная установка................................................................................... |
227 |
14.3. Совмещенная характеристика насоса и трубопровода........................... |
231 |
14.4. Регулирование режимов работы насоса................................................... |
232 |
14.5. Выбор основных параметров центробежного насоса ............................. |
234 |
14.6. Пример расчета колеса центробежного насоса....................................... |
239 |
15. Истечение жидкости................................................................................... |
244 |
15.1. Истечение жидкости через отверстия...................................................... |
244 |
15.2. Истечение жидкости через насадки......................................................... |
246 |
15.3. Истечение жидкости при переменном напоре......................................... |
247 |
15.4. Принцип работы простейшего карбюратора........................................... |
251 |
15.5. Расчет простейшего карбюратора............................................................ |
253 |
16. Устройство, принцип действия и основы расчета двигателя внеш- |
|
него сгорания..................................................................................................... |
257 |
16.1. Идеальный цикл Стирлинга..................................................................... |
257 |
16.2. Основные формулы, описывающие протекание процессов цикла дви- |
|
гателя Стирлинга............................................................................................... |
260 |
16.3. Принцип действия двигателя Стирлинга................................................. |
262 |
16.4. Схема работы двигателя Стирлинга с кривошипно-шатунным меха- |
|
низмом и его расчет........................................................................................... |
264 |
Приложения....................................................................................................... |
272 |
Библиографический список ............................................................................ |
281 |
108
ВВЕДЕНИЕ
Надежность, долговечность, экономичность и экологические показатели современных тепловых двигателей зависят от выбранной схемы кривошипно-шатунного механизма, равномерности хода, уравновешенности, величины крутильных колебаний, способа подачи топлива, управления процессом сгорания.
Современный двигатель не может быть создан без точных расчетов всех его систем, механизмов, узлов, деталей. Расчеты выполняются с использованием теоретических и практических знаний, полученных по многим специальным дисциплинам с применением матема-
тических методов.
Первые три главы пособия посвящены основным вопросам дифференциального и интегрального исчисления функции одной действительной переменной.
Дифференциальное исчисление раздел математики, в котором изучаются способы вычисления производных, дифференциалов и их применение к исследованию свойств функций.
Интегральное исчисление раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения (определения работы, площади, объемов). Именно с созданием дифференциального и интегрального исчисления связывают возникновение «высшей математики». С их появлением получен аппарат, позволяющий анализировать различные процессы, что важно для объяснения физических явлений и построения научной картины мира.
Без помощи производных и интегралов практически невозможно исследовать функции, характеризующие зависимость одних величин от других. Законы природы и техники можно описать с использованием производных и интегралов. Например, соотношения между пройденным расстоянием и скоростью движения, уравнением кривой и площадью под этой кривой представляют собой те конкретные вопросы, на основе которых сложились дифференциальное и интегральное исчисления. Понятия производной и интеграла применимы не только к перечисленным вопросам, но и к самым различным областям науки и техники. В качестве примера следует назвать исследование горения топлива в цилиндрах двигателей внутреннего сгорания, колебательные процессы в механических, гидравлических и электрических системах.
109
Производная, интеграл, теорема Ньютона − Лейбница связаны между собой и представляют определённый язык, приспособленный для описания различных законов природы и техники.
Важными для конструктора являются знания, приобретенные по физике, термодинамике, теории рабочих процессов, теоретической механике, материаловедению, сопротивлению материалов, динамике и другим дисциплинам.
Анализ процессов сгорания углеводородных топлив в цилиндре двигателя производится на основе термодинамики. Превращение химической энергии топлива в механическую происходит в результате осуществления рабочего цикла, представляющего собой законченную совокупность физических и химических процессов, периодически повторяющихся в цилиндрах двигателя.
Моделями первого теоретического приближения рабочих циклов двигателей являются циклы с изохорным, изобарным и смешанным подводом теплоты. Сгорание топлива в камерах необходимо для создания давления в цилиндре и происходит при высокой температуре (выше 2000 К), а это требует охлаждения двигателя и расчета теплообменных аппаратов.
Поступательное движение основных деталей двигателя (поршня, плунжера насоса высокого давления, впускных и выпускных клапанов) ограничены размерами кривошипа, шатуна, формой и размерами кулачка. При определении пути указанных деталей необходимо учитывать конструктивные особенности данных узлов.
Для преобразования поступательного движения поршня в цилиндре во вращательное движение коленчатого вала служит кривошипношатунный механизм (КШМ). Этот механизм является главным для двигателя.
Все процессы в работающем двигателе переменны. При движении поршня в цилиндре изменяется во времени его скорость и ускорение. Изменение скорости и ускорения поршня по времени определяются при помощи производных.
Динамика изучает движение деталей КШМ под действием давления газов и сил инерции. Динамический расчет двигателя позволяет определить силы и моменты в деталях КШМ, что необходимо при расчете их на прочность.
Важным для двигателя является его равномерность хода, плавное движение с места. Указанные параметры двигателя зависят от пра-
110
вильного расчета и выбора размеров, массы маховика. Методика расчета маховика и пример расчета приведены в данном учебном пособии.
По данным теплового расчета двигателя построена индикаторная диаграмма. Линии сжатия и расширения на ней определялись при использовании «текущей» величины сжатия и степени расширения. Расчет индикаторной работы цикла осуществлялся с использованием
определенного интеграла.
Качество процесса подачи топлива оценивалось дифференциальной и интегральной характеристиками. В работе приведена методика их построения и показан расчет на электронных вычислительных машинах (ЭВМ). Дан расчет мелкости распыливания топлива.
Для расчета коленчатого вала на крутильные колебания необходимо иметь значение моментов инерции вала и маховика. В учебном пособии дано их определение. Приведены дифференциальные уравнения свободных и вынужденных крутильных колебаний вала с одной массой, дано их решение.
Представлены гидравлические расчеты трубопроводов (каналов) систем двигателя, дана методика расчета центробежного насоса. При определении времени вытекания жидкости через отверстие из резервуара при переменном напоре использовалось интегральное исчис-
ление.
Двигатели внутреннего сгорания вырабатывают более 60 % энергии, используемой человеком (транспорт, сельское хозяйство, строительство, энергетика, добыча нефти, газа). Любая машина (транспортная, воздушная, морская, строительная, дорожная) в своем составе имеет двигатель. В данном учебном пособии предложена методика расчета систем и механизмов двигателей внутреннего сгорания при помощи математических методов. Пособие может быть полезно студентам любой технической специальности, которые изучают дисциплину «Высшая математика».
В учебном пособии приведены материалы по расчету систем и механизмов тепловых двигателей с использованием интегрального и дифференциального исчисления.
Целью учебного пособия является формирование знаний у студентов специальности 140501 «Двигатели внутреннего сгорания» по дисциплине «Высшая математика» и ее приложение при проектировании, расчете двигателей, его систем, механизмов.
111
1. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
1.1.Понятие производной функции
Впроцессе решения задач, возникающих в физике, химии, технике, достаточно часто приходится сталкиваться с зависимостями одних величин от других, с так называемыми функциональными зависимостями (функциями). Функциональная зависимость одной величины у от другой величины х означает, что каждому значению х соответствует определенное значение у. Величина х при этом называется
независимой переменной (аргументом), а у – зависимой перемен-
ной (функцией). В переводе с латинского функция означает «исполнение». Функция является одним из основных математических поня-
тий.
Обозначается функция следующим образом: y y x ; y f x .
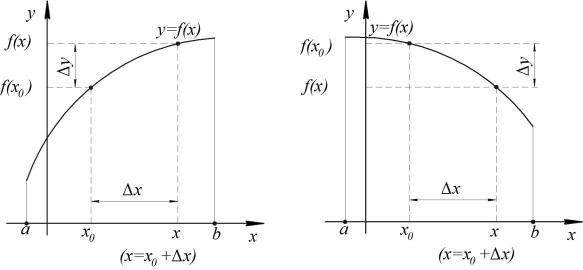
Пусть функция y f (x) определена в некотором интервале a;b (рис. 1.1, а, б). Возьмем произвольную точку x0 a;b . Для любого
x a;b |
разность x x0 называется приращением аргумента |
x в |
|
точке x0 |
и обозначается x (читается как «дельта икс») |
|
|
|
|
x x x0 . |
(1.1) |
Следовательно, |
x x0 x (см. рис. 1.1, а, б). Обозначение |
||
x0 a;b означает, |
что точка х0 принадлежит интервалу a;b . |
|
|
а) |
б) |
Рис. 1.1. Приращение аргумента и приращение функции
112
