
2471
.pdfтуры (не важно какой) до температуры Т. Очевидно, что Q зависит от Т: Q Q T . Тогда для нагревания 1 кг вещества от температуры T1 до температуры T2 понадобится Q T1,T2 Q T2 Q T1 − теплоты; для нагревания тела от температуры T до T T 0С ( T очень малое приращение температуры) понадобится
Q T T Q T Q − теплоты. |
|
|||||
Поэтому средняя теплоемкость |
cср на участке от |
T до |
||||
T T 0С определится как отношение |
|
|
|
|
|
|
сср |
Q T T Q T |
|
Q |
. |
(1.14) |
|
|
|
|||||
|
T |
|
|
T |
|
|
Мгновенная теплоемкость cмгн (прилагательное «мгновенная» в данном случае относится не к определенному моменту времени, а к фиксированной температуре T тела) определяется как значение сср, отвечающее очень маленькому приращению Т температуры, причем полученное таким путем значение теплоемкости cмгн будет тем точнее, чем меньшее Т мы берем. Заметим, что в подавляющем большинстве случаев уже значение Т 1 0С (1 К) будет достаточно мало для точного определения величины с с Т . Здесь выражение «достаточно мало» означает, что полученное таким путем значение теплоемкости с практически не будет отличаться от значения, к которому мы придем, выбрав меньший интервал Т изменения температуры.
Таким образом,
cмгн |
QT lim |
Q T T Q T |
|
lim |
Q |
. |
(1.15) |
|
|
||||||
|
T 0 |
T |
T 0 T |
|
|||
Проиллюстрируем сказанное выше на примере нагревания 1 кг стали от 0 до Т 0С. Количество теплоты Q Q T , необходимое для нагревания 1 кг стали от 0 до Т 0С, дается следующей эмпирически наблюдаемой зависимостью [11]:
Q T 440,857T 0,29725T2.
Тогда в соответствии с вышесказанным
123
сср |
|
Q |
|
Q T T Q T |
|
|
440,857 T T 0,29725 T T 2 |
|
||||
|
|
|
T |
|||||||||
|
|
T |
T |
|
|
|
|
|||||
|
|
|
440,857T 0,29725T2 |
|
||||||||
|
|
|
|
|
|
|
440,857 0,5945T 0,29725 T . |
|
||||
|
|
T |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|||||
|
|
|
cмгн |
lim |
Q |
lim 440,857 0,5945T 0,29725 T |
|
|||||
|
|
|
T |
|
||||||||
|
|
|
|
|
|
T 0 |
T 0 |
|
||||
|
|
|
|
|
|
|
|
440,857 0,5945T . |
|
|||
Аналогичный результат мы получим более коротким путем, про-
дифференцировав выражение Q T 440,857T 0,29725T2 по переменной Т, воспользовавшись таблицей производных (табл. П.1.1):
Q T 440,857T 0,29725T2 440,857 0,5945T .
Таким образом, с(0) 440,857 Дж/(кг∙град), а например,
с(100) 440,857 0,5945 100 500,307 Дж/(кг∙град). Обычно массо-
вую удельную теплоемкость с выражают в Дж/(кг∙К) (К − градус по шкале Кельвина).
Рассмотрим также вариант графического решения задач на нахождение производной функции на примере задачи 1.2 и примера 1.2 (нахождение скорости по графику функции перемещения).
Задача 1.2. Пусть материальная точка движется по закону
S t2 , где S=S(t) – функция зависимости пути от времени; t время. Найти графически изменение скорости движения материальной точки за промежуток времени от нуля до двух секунд.
Замечание. Как и в задаче 1.1, для соблюдения требований раз-
мерности считаем S k t2, где коэффициент k имеет размерность м / с2. В нашем случае считаем k 1 м/с2.
Решение. Построим график зависимости пути от времени. Пусть вертикальная ось соответствует перемещению S, а горизонтальная – времени t (рис. 1.5). По условию задачи t 0;2 . График представляет собой ветвь параболы на участке изменения t от 0 до 2.
124
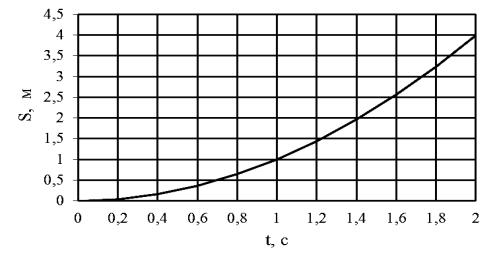
Рис. 1.5. График перемещения материальной точки
Разобьем отрезок [0;2] на 10 частичных отрезков [ti-1 ;ti] равной
длины |
ti = 0,2 |
(i |
принимает значения от 1 до 10). Найдем |
|
Si = S(ti) − S(ti-1) |
− |
изменение пути, соответствующее изменению |
||
времени |
ti на |
каждом участке. Например, на участке [0; 0,2] |
||
S1 = S(t1) − S(t0) = S(0,2) |
− S(0) =0,22 − 02 =0,04; на участке [0,2; 0,4] |
|||
S2 = S(t2) − S(t1) = S(0,4) |
− S(0,2) =0,42 − 0,22 =0,16 − 0,04=0,12. Ре- |
|||
зультаты заносим в табл. 1.1.
Таблица 1.1
Определение скорости движения материальной точки
ti , |
Si=S(ti ), |
Si , |
ср i= Si /Δ t, |
с |
м |
м |
м/с |
0 |
0 |
0 |
0 |
0,2 |
0,04 |
0,04 |
0,2 |
0,4 |
0,16 |
0,12 |
0,6 |
0,6 |
0,36 |
0,2 |
1 |
0,8 |
0,64 |
0,28 |
1,4 |
1 |
1 |
0,36 |
1,8 |
1,2 |
1,44 |
0,44 |
2,2 |
1,4 |
1,96 |
0,52 |
2,6 |
1,6 |
2,56 |
0,6 |
3 |
1,8 |
3,24 |
0,68 |
3,4 |
2 |
4 |
0,76 |
3,8 |
Далее на каждом интервале найдем отношение Si /Δ ti. Это отношение равно средней скорости движения материальной точки cp i на каждом участке изменения времени (см. п. 1.1). Результаты также заносим в табл. 1.1. Используя полученные данные (первый и четвер-
125
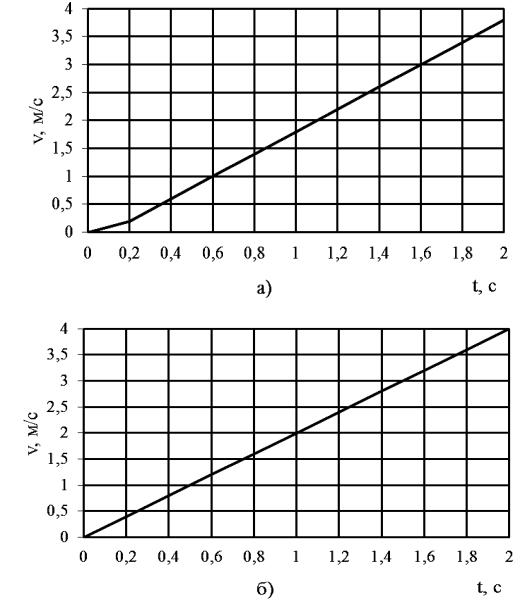
тый столбцы табл. 1.1), в координатах V – t обозначаем точки (ti; cp i) (рис. 1.6, а). Плавно соединив эти точки, строим график изменения средней скорости движения материальной точки c течением времени
(см. рис. 1.6, а).
Рис. 1.6. Скорость движения материальной точки
Получить график изменения скорости движения материальной точки за данный промежуток времени можно предварительно отыскав производную пути по времени. Согласно формуле (1.7) St , следо-
вательно, в нашем примере =S t t2 2t. То есть график изменения скорости движения материальной точки в координатах − t
126
представляет собой прямую линию (рис. 1.6, б). Сравнительный анализ рис. 1.6, а и 1.6, б показывает, что эти графики практически совпадают. Точный график скорости движения материальной точки изображен на рис. 1.6, б. С уменьшением ti график рис. 1.6, а будет в большей степени соответствовать графику, изображенному на
рис. 1.6, б, в связи с тем, что lim cp |
lim |
S |
[формула (1.3)]. |
|
t |
||||
t 0 |
t 0 |
|
Пример 1.2. Графическое решение задачи нахождения скорости поршня по его перемещению.
Рассмотрим движение поршня в кривошипно-шатунном механизме (КШМ) двигателя внутреннего сгорания. КШМ служит для преобразования возвратно-поступательного движения поршня во вращательное движение коленчатого вала (кривошипа).
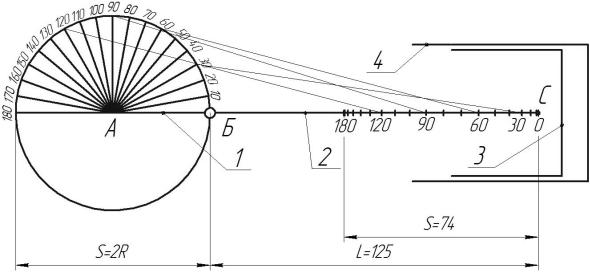
При вращении кривошипа 1 (рис. 1.7) длиной АБ и радиусом R точка Б описывает окружность. Разобьем половину окружности на 18 точек через 100. Кривошип перемещает шатун 2, который в точке С соединен при помощи пальца с поршнем 3. Поршень под действием давления газов совершает движение по оси цилиндра 4.
Рис. 1.7. Определение пройденного пути поршнем в зависимости от положения кривошипа (угла φ)
Выполним чертеж КШМ в определенном масштабе (например, 1:1). В нашем примере радиус кривошипа R=37 мм, а длина шатуна L=125 мм. Конструктивный параметр КШМ λ = R/L для автомобиль-
127
ных двигателей лежит в пределах 0,25 0,35. Частота вращения кривошипа 5600 мин-1 (двигатель типа ВАЗ).
За исходное примем положение, когда ось кривошипа 1 и шатуна 2 совмещены с осью цилиндра 4. Для анализа движения поршня важны три его функции путь, скорость, ускорение, зависящие от времени или угла поворота φ кривошипа.
Рассмотрим перемещение поршня 3 от точки С по оси цилиндра 4 при повороте кривошипа 1 на 10, 20 , 300 и т. д. до 1800. От 180 до 3600 движение поршня симметрично, и на данном участке измерения не производим. При повороте кривошипа, например, на 300 шатун следует за кривошипом и перемещает поршень (смотрите отметки на оси цилиндра). Приращение хода поршня (изменение функции) обозначим через S. Результаты измерений заносим в табл. 1.2, по данным которой строим график зависимости перемещения поршня S от угла поворота кривошипа φ (рис. 1.8).
Таблица 1.2
Изменение перемещения и скорости поршня в зависимости от угла поворота кривошипа
φ, |
Перемещение |
Приращение |
Скорость |
|
хода поршня |
поршня , |
|||
град |
поршня S, мм |
|||
(функции) S, м |
м/с |
|||
|
|
|||
0 |
0 |
0 |
0 |
|
10 |
0,72 |
0,72·10 -3 |
2,42 |
|
20 |
2,87 |
2,15·10 -3 |
7,16 |
|
30 |
6,33 |
3,46·10 -3 |
11,53 |
|
40 |
10,93 |
4,60·10 -3 |
15,33 |
|
50 |
16,47 |
5,54·10 -3 |
18,46 |
|
60 |
22,67 |
6,20·10 -3 |
20,66 |
|
70 |
29,27 |
6,60·10 -3 |
22,00 |
|
80 |
36,00 |
6,73·10 -3 |
22,43 |
|
90 |
42,60 |
6,6·10 -3 |
22,00 |
|
100 |
48,85 |
6,25·10 -3 |
20,83 |
|
110 |
54,58 |
5,73·10 -3 |
19,10 |
|
120 |
59,67 |
5,08·10 -3 |
16,93 |
|
130 |
64,00 |
4,37·10 -3 |
14,56 |
|
140 |
67,30 |
3,3·10 -3 |
11,00 |
|
150 |
70,00 |
2,70·10 -3 |
9,00 |
|
160 |
72,00 |
2·10 -3 |
6,60 |
|
170 |
73,98 |
1·10 -3 |
3,30 |
|
180 |
74,00 |
0 |
0 |
128
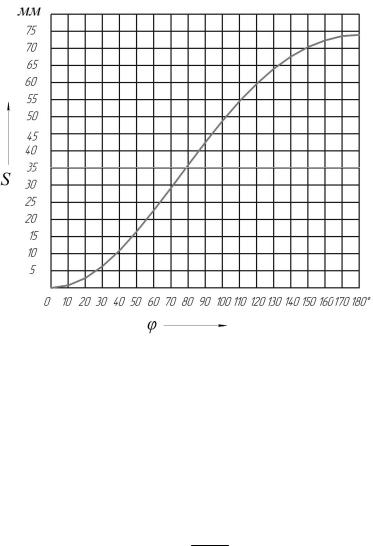
Рис.1.8. Зависимость перемещения поршня от угла поворота кривошипа
Функция S=S(φ) является исходной (начальной) и с ее помощью можно получить другие функции, например, скорости, ускорения поршня в зависимости от угла или времени поворота кривошипа. Заметим, что путь поршня можно определить и расчетным способом по формуле (см. гл. 4)
S R (1 cos ) R (1 cos2 ). 4
Для определения скорости и ускорения поршня необходимо знать время в секундах при повороте кривошипа на 100. Время в секундах, угол φ в градусах и частота вращения кривошипа n (мин-1) связаны выражением
t / 6 n 10/ 6 5600 3 10 4 c.
Для каждого участка в интервале 100 приращение аргумента равно 3·10–4 c. Чтобы определить скорость поршня при повороте кривошипа от 0 до 180 0 в интервале через 100, необходимо приращение пути S (м) на каждом участке разделить на приращение аргумента t = 3·10– 4 c. Получим значение средней скорости (м/с) на каждом участке и занесем в табл. 1.2. Для определения ускорения поршня
приращение скорости |
на каждом расчетном участке делим на |
приращение аргумента |
t = 3·10– 4 c. |
|
129 |
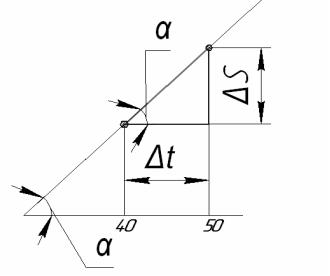
Например, рассмотрим рис. 1.8 на участке изменения пути, от 40 до 500. Выделим прямоугольный треугольник, один из катетов которого численно равен приращению пути S=5,54 мм (ΔS=16,47 – 10,93=5,54) (данные табл. 1.2), а другой − приращению времени t=3·10 – 4 c. В рассматриваемом прямоугольном треугольнике отношение S/ t численно равно тангенсу угла (рис. 1.9):
tg S / t 5,54 10 3 / 3 10 4 18,46. С другой стороны, это отношение равно средней скорости движения поршня на данном участке пути за данный промежуток времени. То есть при приращении пути поршня на данном участке, равном 5,54·10-3 м за время 3·10 – 4с, средняя скорость достигнет 18,46 м/с.
|
Таким образом, |
средняя |
|
||||
скорость поршня |
на каждом |
|
|||||
участке |
изменения |
времени |
|
||||
равна отношению |
|
прираще- |
|
||||
ния пути к приращению вре- |
|
||||||
мени. По полученным данным |
|
||||||
табл. 1.2 мы можем построить |
|
||||||
график |
изменения |
средней |
|
||||
скорости движения поршня в |
|
||||||
КШМ. Однако, как и в преды- |
|
||||||
дущей |
задаче 1.2, |
чем |
мень- |
|
|||
шие |
значения |
t |
мы |
будем |
|
||
брать (меньше шаг расчета), |
Рис. 1.9. Определение средней скорости |
||||||
тем точнее полученный гра- |
|||||||
фик |
будет |
соответствовать |
поршня |
||||
действительному графику скорости движения поршня. Такой подход к решению рассматриваемой задачи согласуется с определением производной функции как предела отношения приращения функции к приращению аргумента при стремлении последнего к нулю (малому значению) и иллюстрирует ее механический смысл. Напомним, что производная является скоростью изменения процесса, а в нашем примере скоростью движения поршня.
На рис. 1.10 представлен график изменения скорости движения поршня (первой производной пути по времени) в зависимости от угла поворота кривошипа φ или соответствующего времени.
130
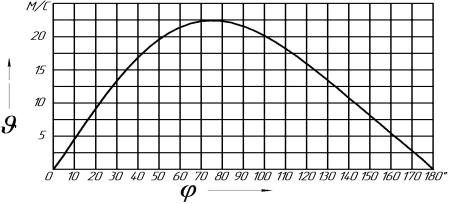
Рис. 1.10. Зависимость скорости поршня от угла поворота кривошипа
Следует отметить, что график пути поршня в зависимости от положения кривошипа существенно отличается от графика скорости поршня как по форме, так и по единицам величины (м и м/с). Ход поршня не зависит от частоты вращения кривошипа, а скорость зависит. Таким образом, используя понятие производной, расчетным путем из исходного графика пути поршня мы получили новый график зависимости скорости поршня от угла поворота кривошипа.
Зная приращение скорости на отдельных участках, можно обратным путем определить приращение пути. Например, при повороте кривошипа от 40 до 500 среднее значение скорости равнялось (15,33 + +18,46)/2 = 16,89 м/с. Умножим полученное значение скорости на время 3·10– 4 c, соответствующее 100 (шагу расчета), получим среднее приращение пути, равное 5,06·10-3 м. Полученный результат согласу-
ется с данными табл. 1.2 (4,6·10-3 + 5,5·10-3)/2 = 5,05·10-3 м).
Теорема 1.1. (Связь между непрерывностью и дифференцируемостью функции). Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Непрерывность функции в точке x0 означает, что функция имеет в этой точке предел, равный значению функции в этой точке: lim f x f x0 . Или, что то же самое, каждому бесконечно малому
приращению аргумента x [формула (1.1)] функции y f x соответствует бесконечно малое приращение функции y, определенное по формуле (1.2), то есть lim y 0. Графически непрерывность
функции в точке означает, что график функции в этой точке строится «не отрывая руки».
131
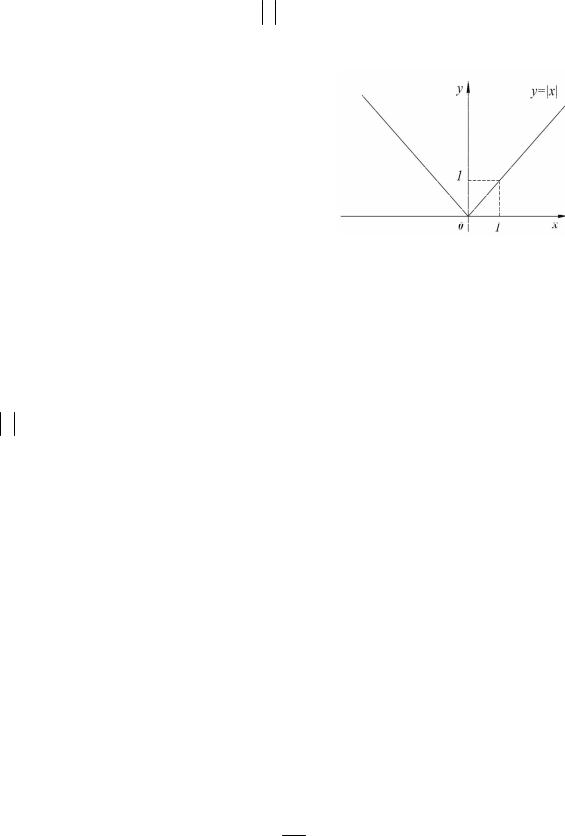
Заметим, что обратное утверждение неверно, так как непрерывная в данной точке функция может и не иметь в ней производной. Например, речь идет о функции y x . На рис. 1.11 представлен ее график.
Данная функция непрерывна в точке x0 0, однако производной в этой точке функция не имеет. Покажем почему. Для этого по определению производной посчитаем предел:
lim |
y |
|
lim |
y(x0 x) y(x0) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 0 x |
x 0 |
x |
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
|
y(0 x) y(0) |
lim |
|
|
x |
|
|
0 |
|
|||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|||||||||||||
x 0 |
x |
x 0 |
|
Рис. 1.11. График функции |
||||||||||||||||||
|
|
|
|
|
x |
|
|
|
1, x 0 |
|
|
|
|
|
|
|
|
|
y=|x| |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim |
|
|
|
|
|
|
|
. Следователь- |
||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
x 0 x |
1, x 0 |
|
|
|
|
y |
|
|
||||||||||||||
но, в точке x0 0 предел lim |
|
не существует, а значит, функция |
||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 0 x |
|
|||||||||
y x не имеет в этой точке производной.
Найдем по определению производные некоторых элементарных
функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1.3. Найти производную функции y x2. |
|
|
|
|
|
|||||||||||||||
Решение. Функция y x2 |
непрерывна в каждой точке действи- |
|||||||||||||||||||
тельной оси Ох. Найдем предел |
lim |
y |
. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x 0 x |
x x |
2 |
|
2 |
|
|
||||||
|
|
y |
|
|
y(x x) y(x) |
|
x |
|
|
|||||||||||
x2 |
lim |
lim |
lim |
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|||||||||||||
|
|
x 0 x |
x 0 |
|
x |
|
|
x 0 |
|
|
|
|
|
|
||||||
lim |
x2 |
2x x x 2 x2 |
lim |
2x x x 2 |
|
lim |
x 2x x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|||||||
x 0 |
|
|
|
x 0 |
|
|
x 0 |
|
|
x |
||||||||||
lim 2x x 2x.
x 0
Пример 1.4. Найти производную функции y x3.
Решение. Функция y x3 непрерывна в каждой точке действи-
тельной оси Ох. Найдем предел lim y.
x 0 x
132
