2471

также первым замечательным пределом lim sin 1 (в нашем случае

0

x).

Аналогично можно найти производную функции y sin x:

sin x cosx.

Обратим внимание на то, что функции y sin x и y cosx играют важную роль в расчетах двигателей внутреннего сгорания. С их помощью описывают движение поршня (гл. 4); свободные и вынужденные крутильные колебания вала (гл. 9), работу турбины двигателя

133

(гл. 12), движение жидкостей в трубопроводах и работу, совершаемую в насосных установках (гл. 14).

Графики периодических функций y sin x и y cosx представлены на рис. 1.12, а, б. Наименьший положительный период этих функций T 2 , при этом справедливы формулы sin x 2 k sin x; cos x 2 k cosx (k= 0; ±1; ±2; ±3; …).

Рис. 1.12. Графики функций: а) y=sin x; б) y=cos x

1.1.2. Основные правила дифференцирования

Пусть u u(x), (x) − дифференцируемые в некотором интервале a;b функции. Сформулируем для них правила дифференцирования.

1. Производная произведения функции на константу равна произведению константы на производную данной функции (константа выносится за знак производной).

Заметим, что данное правило распространяется на случай, когда число слагаемых 2.

3. Производная произведения двух функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй.

134

(x) 0) равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель равен квадрату знаменателя исходной дроби.

1.1.3. Производная сложной функции

Пусть y f (u) и u (x), тогда y f ( (x)) − сложная функция с промежуточным аргументом и и независимым аргументом х.

Тогда, если функция u (x) имеет производную ux в точке х, а

Таким образом, для нахождения производной сложной функции необходимо сделать следующее: производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

В том случае, когда функция содержит несколько промежуточных аргументов, это правило остается в силе (см. пример 1.7).

Пример 1.6. Найти производную функции y 3sin x 2.

Данная функция является сложной. Ее можно представить в виде

1

цепочки простых функций: y u 3 ,u sin x 2. Следовательно, воспользовавшись формулой (1.20), получим

1

cosx. 3 3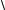 sin x 2 2

135

Пример 1.7. Найти производную функции y ctg3 ln 3x 1 .

Данная функция также является сложной. Как и в предыдущем примере, ее можно представить в виде цепочки простых функций: y u3, u ctg v, v lnq, q 3x 1.

Тогда yx yu uv vq qx 3u2 sin12 v 1q 3 3ctg2 ln 3x 1

sin2 ln13x 1 3x1 1 3 −9∙ctg2 ln 3x 1 sin2 ln13x 1 3x1 1.

1.1.4.Производная обратной функции

Пусть y f (x) и x (y) − взаимно-обратные функции. Тогда, если функция y f (x) строго монотонна на интервале

a;b и имеет неравную нулю производную fx в произвольной точке

Пример 1.8. Найти производную функции y arctgx.

Для решения задачи рассмотрим обратную функцию x tgy. По

формуле производной обратной функции (1.21): yx 1 . Следова- xy

В процессе преобразований мы воспользовались следующими тригонометрическими формулами:

Пример 1.9. Найти производную функции y 54x 5, используя формулу производной обратной функции.

По формуле (1.21) yx 1 . Следовательно, xy

136

Производные основных элементарных функций записаны в виде таблицы (см. табл. П.1.1). Заметим, вывод этих формул основан на определении производной и на приведенных выше правилах нахождения производной.

Пример 1.10. Найти производные следующих функций:

а) y cos7x 63x tg4 ln2x; б) y ctg 3x 8 arccos2 7x;

x 3 2

в) y ln3 5x 6 .

Решение

а) Для нахождения производной функции y cos7x 63x tg4ln2x необходимо воспользоваться правилом дифференцирования суммы двух и более функций [формула (1.17)], а также правилом дифференцирования сложной функции [формула (1.20)], поскольку функции cos7x,63x,ln2x − сложные.

б) Для нахождения производной функции y ctg3x 8 arccos27x необходимо воспользоваться правилом дифференцирования произведения двух функций [формула (1.18)], а также правилом дифференцирования сложной функции [формула (1.20)], поскольку функции ctg 3x 8 , arccos2 7x − сложные.

137

димо воспользоваться правилом дифференцирования частного двух функций [формула (1.19)], а также правилом дифференцирования сложной функции [формула (1.20)], поскольку функцииx 3 2,ln3 5x 6 − сложные.

y x2 4.

138

Под неявным заданием функции понимают ее задание в виде уравнения F x, y 0, не разрешенного относительно y. Например,

уравнение по x, рассматривая при этом y как функцию от x (y=y(x)), а затем полученное уравнение (если это необходимо) разрешить относительно y .

Решение. Согласно правилу дифференцирования неявно заданной функции, продифференцируем уравнение по x, рассматривая при этом y как функцию от x, то есть y y x .

y 21x 21y 2sin y y 21x 1 42yysin y

Пример 1.12. Найти производную функции y, заданной неявно

уравнением arcsin x yln x. y

Решение. Рассуждая аналогично, получаем:

139

на отрезке t1;t2 . Каждому значению t t1;t2 соответствуют определенные значения x, y, которые в свою очередь на координатной плоскости Oxy являются координатами некоторой точки P(x, y). Когда t изменится от t1 до t2, точка P на координатной плоскости Oxy опишет некоторую кривую.

Определение. Уравнения x x(t), y y(t) (t t1;t2 ) называют-

ся параметрическими уравнениями кривой, t параметром, а спо-

соб задания кривой параметрическими уравнениями − параметриче-

ским.

Заметим, что в математике параметр (от греч. «parametron» − «отмеривающий») − это величина, числовые значения которой позволяют выделить определенный элемент (например, кривую) из множества элементов (кривых) того же рода. В технике параметр − это величина, характеризующая какое-либо свойство процесса, явления или системы, машины, прибора (например, электрическое сопротивление, теплоемкость, масса, коэффициент трения).

Пусть x и y заданы как функции некоторого параметра t:

x x(t),

y y(t),

140

где x(t), y(t) − имеют необходимое число производных по переменной t в рассматриваемой области изменения этой переменной. Тогда производная функции y f x , определяемой параметрическими