
- •1. ПОНЯТИЕ НАУКИ. КЛАССИФИКАЦИЯ НАУК
- •5. ВИДЫ ИССЛЕДОВАНИЙ
- •7.1. Классификация методов, используемых в исследованиях
- •7.3. Общенаучные методы исследования
- •8. СУЩНОСТЬ ОЦЕНИВАНИЯ
- •Экспертные методы получения первичной информации
- •11. МЕТОДЫ АНАЛИЗА
- •11.1. Детерминированные и стохастические процессы
- •11.2. Классификация методов анализа, используемых в исследованиях
- •11.2.1. Вариационный анализ
- •11.2.2. Дискриминантный анализ
- •11.2.3. Корреляционно-регрессионный анализ
- •11.3.1. Древовидные графы
- •11.3.2. Диаграмма «рыбий скелет»
- •11.4. Математические методы исследования
- •12. ОБЪЕКТ ИССЛЕДОВАНИЯ И ЕГО СВОЙСТВА
- •13. МОДЕЛИ, ИХ КЛАССИФИКАЦИЯ
- •13.1. Построение моделей
- •13.2. Методы имитационного моделирования
- •13.3. Основные этапы имитационного моделирования
- •13.5. Формализация имитационной модели
- •15. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- •15.1. Классификация планов
- •15.2. Область определения, интервалы варьирования и уровни факторов. Кодирование факторов
- •15.4. Дробный факторный эксперимент
- •15.7. Экстремальный эксперимент
- •ЗАКЛЮЧЕНИЕ
- •Библиографический список
11.3.1. Древовидные графы
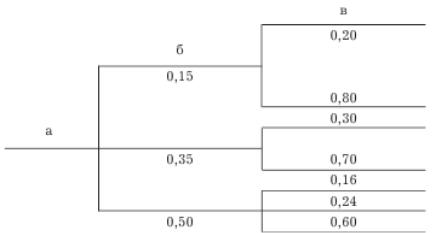
Общий вид древовидного графа – порфириана, приведен на рис. 9. Ориентация графа может быть различной: горизонтальная или вертикальная, прямая или обратная, в зависимости от удобства представления тех понятий, которые отражаются с его помощью. Так, известная в технологии машиностроения сборочная вилка Кнеппеля имеет в д зеркальный, приведенный на рис. 9 [4].
Древов дные графы чаще всего используются для декомпозиции |
||||
проблемы / цели / задачи на подпроблемы / подцели / подзадачи с це- |
||||
они |
в |
|||
лью упрощен я сложного, доведения его до элементарного. Иногда |
||||
Сиспользуются для агрегирования простых явлений, для свертки |
||||
частных показателей в о о щающий. Для решения, в частности, этой |
||||
задачи было предложено применять к ветвям дерева коэффициенты |
||||
бА |
||||
относительной важности, получаемые путем экспертного оценивания. |
||||
|
|
|
Д |
|
|
а |
|
||
|
|
|
||
|
|
|||
Рис. 9. Общий вид простого древовидного графа: |
||||
|
|
а – ствол; б – сук; в |
И |
|
|
|
– ветви; |
||
0,15 – значение коэффициента относительной важности ветви
Такой синтез двух разных методов (графического представления и экспертного оценивания) был впервые использован сотрудниками компании «Хониуэлл» (США) Эшем и Джестисем и был назван «Помощь планированию с использованием техники присвоения коэффициентов относительной важности». Пример графа с присвоенными коэффициентами важности приведен на рис. 9 [4].
При присвоении значений коэффициентов важности следует помнить, что сумма коэффициентов ветвей одного уровня всегда равна единице. При качественной структуризации проблемы и как следует оцененной весомости каждой ветви не составляет труда опреде-
50
лить вклад каждой из ветвей самого детализованного уровня (на рис. 9 справа) в проблему / цель / задачу, отраженную стволом
графа. Так, ветвь в графа, представленного на рис. 9, характеризуется |
|||
вкладом в 0,03, т.е. в 3%, (0,20 · 0,15) в общую проблему (ствол а), |
|||
порфириан может дополняться не только значениями весомости, но и |
|||
С |
|
||
значениями вероятностей наступления ветвей. |
|||
|
|
|
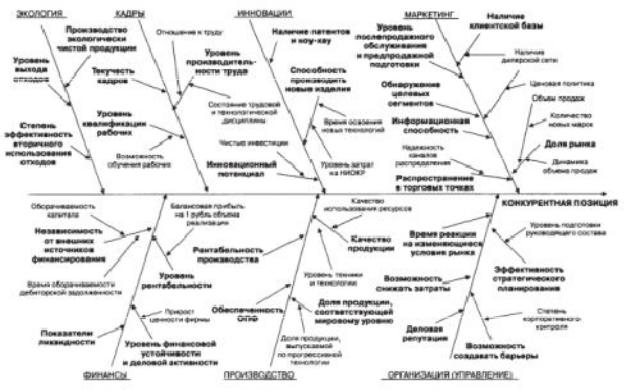
11.3.2. Диаграмма «рыбий скелет» |
Особую разнов дность порфириана, обусловленную формой |
|||
представлен я, |
составляет граф, предложенный японским профессо- |
||
ром Ис кава |
получ вший название – диаграмма «рыбий скелет». |
||
Общий в д графа пр веден на рис. 10 [4]. |
|||
Графы т па «ры й скелет», чаще всего используемые для уяс- |
|||
нения |
представлен я причинно-следственных связей между факто- |
||
( |
сточн ками, составными частями и т.д.) проблемы, также мо- |
||
рами |
|||
гут дополняться значениями коэффициентов весомости или вероят- |
|||
ности наступлен я факторов. Диаграмма может строиться по резуль- |
|||
татам, например, мозгового штурма проблемы [4]. |
|||
|
бА |
||
Д И
Рис. 10. Диаграмма «рыбий скелет»
51
