
1711
.pdf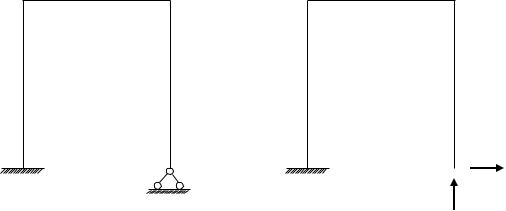
Заданная систeма |
Основная сис- |
|
тема метода сил |
Х1
Х2
Рис. 6.1
Из выражения (6.2) очевидно, что рама, изображённая на рис. 6.1, является дважды статически неопределимой системой.
Статически неопределимые системы обладают следующими свойствами:
1.В статически неопределимых системах, по сравнению со статически определимыми, при одной и той же нагрузке значения внутренних усилий получаются меньшими.
2.Статически неопределимые системы являются более жёсткими по сравнению со статически определимыми.
3.Разрушение «лишних» связей в статически неопределимых системах не ведёт к разрушению всей системы.
4.В статически неопределимых системах температурные воздействия и осадка опор вызывают появление дополнительных усилий в отличие от статически определимых систем.
6.2.Основная система метода сил
Вметоде сил основную систему выбирают из заданной, устраняя «лишние» связи. За «лишние» могут быть приняты как внешние, так и внутренние связи. Внешние связи являются опорными связями, а внутренними являются связи, препятствующие взаимному перемещению двух смежных сечений при мысленном рассечении стержня или удалении из него шарнира.
Для любой статически неопределимой системы существует несколько вариантов основной системы.
Рациональной основной системой является такая, для которой при её решении наиболее просто составляются уравнения статики.
Основная система метода сил должна быть желательно статически определимой и геометрически неизменяемой.
Для того чтобы основная система оставалась эквивалентна заданной,
70

вместо устранённых «лишних» связей ставят неизвестные усилия Х.
На рис. 6.2 приведены два варианта основной системы. В качестве «лишних» связей выбраны внешние.
Заданная система |
Основная система |
Основная система |
|
метода сил |
метода сил |
||
|
І |
ІІ |
вариант |
вариант |
Х1 |
Х1 |
Х2 |
Х2 |
Рис. 6.2
Наиболее простым представляется ІІ вариант основной системы.
На рис. 6.3 для заданной системы приведена основная система, где за «лишние» выбраны внутренние связи, полученные путём мысленного устранения внутреннего шарнира.
Основная система, принятая для расчёта и нагруженная внешней нагрузкой и усилиями Х, приложенными вместо устранённых связей, будет эквивалентна заданной в случае, если перемещения в этих системах равны между собой.
Если при расчёте удаляются внешние связи, то условием эквивалентности будет равенство нулю перемещений по направлению устранённых связей.
Если за «лишние» связи приняты внутренние, то условием эквивалентности будет равенство нулю взаимных перемещений смежных поперечных сечений в месте разреза системы.
Для заданных систем, имеющих n лишних связей, условие эквивалентности имеет вид
1 0; …; i 0; … ; n 0, (6.3)
где i перемещения по направлению удаленных связей.
Используя принцип независимости действия сил, условие (6.3) запишем в виде
71

i = i1+ i +…+ i +…+ iк +…+ iF = 0, |
(6.4) |
где iк перемещение по направлению i -й удалённой связи, вызванной действием k-й неизвестной силы; iF перемещение по направлению
i- й удалённой связи от действия нагрузки.
|
|
|
|
|
|
|
|
|
|
Х1 |
|
Х1 |
|
|
|
|
|
|
|
|
|
|
|
|
Х2 |
|
Х2 |
|
|
|
|
Заданная |
|
|
|
|
Основная |
|
||||||
|
|
система |
|
|
|
|
система |
|
||||||
|
|
|
|
|
|
|
|
|
|
метода сил |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.3
6.3. Канонические уравнения метода сил
Любое перемещение, вызванное какой-либо силой, для линейно дефомируемых систем можно выразить в виде произведения этой силы на перемещение от действия единичной силы:
ik k ik , |
(6.5) |
где Хk искомое усилие; ik перемещение по направлению |
i - й связи |
основной системы от действия силы Xk = 1.
Для статически неопределимой системы с n «лишними» связями система уравнений имеет вид
X1 11 ... |
Xi 1i ... |
Xn 1n 1F 0; |
|
|
|
|
|
|
|
................................................................. |
|
|||
|
|
Xi ii |
Xn in iF 0; |
(6.6) |
X1 i1 |
||||
................................................................ |
|
|||
|
|
|
|
|
|
|
Xi in |
Xn nn nF 0. |
|
X1 n1 |
|
|||
72

Система (6.6) называется системой канонических уравнений метода сил. В связи с тем, что заданная рассчитываемая статически неопределимая конструкция под действием внешних и внутренних сил находится в равновесии, каждое уравнение системы уравнений (6.6) отрицает наличие перемещений по направлению устранённых связей.
Коэффициенты с одинаковыми индексами называются главными и могут быть только положительными.
Коэффициенты с разными индексами называются побочными, они могут быть как положительными, так и отрицательными. Побочные коэффициенты обладают свойством взаимности, т.е. ij ji .
Коэффициенты iF называются грузовыми и представляют собой перемещения в основной системе в направлении i-й устранённой связи от заданной внешней нагрузки.
6.4. Определение коэффициентов канонических уравнений
Вычисление коэффициентов при неизвестных системы канонических уравнений метода сил и её грузовых членов, представляющих единичные и грузовые перемещения, проводится с помощью известных методов определения перемещений, изложенных в предыдущем разделе.
Обычно при расчёте систем с прямолинейными элементами применяется правило П.Верещагина, в соответствии с которым осуществляется перемножение эпюр. При этом, если рассматриваются так называемые изгибные конструкции (балки, рамы и арки), то определение перемещений ведётся с учётом только изгибающих моментов М, так как перемещения, учитывающие значения продольных N и поперечных Q сил оказываются несопоставимо малыми по сравнению с теми, которые имеют место от действия изгибающего момента М, и ими пренебрегают.
Для определения единичных коэффициентов используют формулу
ik |
Эп.Mi Эп.Mk |
|
i yk |
, |
(6.7) |
|
|
||||
|
EJ |
EJ |
|
||
где Эп.Mi эпюра изгибающих моментов, построенная в основной системе от действия неизвестной силы Хi 1, приложенной в точке устране-
ния i-й «лишней» связи; Эп.Mk эпюра изгибающих моментов, построенная в основной системе от действия неизвестной силы Хi 1, приложен-
ной в точке устранения k-й «лишней» связи; i площадь эпюры изги-
бающих моментов Mi ; yk координата на эпюре Mk , расположенная под
центром тяжести эпюры Mi .
73

Свободные члены системы канонических уравнений (6.6) метода сил определяют по формуле
|
Эп.М 0 Эп. |
|
|
|
|
|
y |
|
|
|
|
|
|
iF |
М |
i |
|
F |
i |
|
|
|
|
||||
|
F |
|
|
, |
|
|
(6.8) |
||||||
|
EJ |
|
|
EJ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
где Эп.MF0 эпюра изгибающих моментов (грузовая эпюра), построенная |
|||||||||||||
в основной системе от действия заданных внешних нагрузок; F |
пло- |
||||||||||||
щадь грузовой эпюры MF0 ; |
yi ордината на эпюре |
|
i , расположенная |
||||||||||
M |
|||||||||||||
под центром тяжести грузовой эпюры MF0 .
Для проверки правильности определения коэффициентов при неизвестных строят в соответствии с выражением (6.9) суммарную единичную
эпюру MS .
|
|
n |
|
||
Эп. |
|
S Эп. |
|
i . |
(6.9) |
M |
M |
||||
|
|
i 1 |
|
||
Правильность определения коэффициентов ik (единичных перемещений) при неизвестных в системе канонических уравнений метода сил в соответствии с универсальной проверкой осуществляется выражением (6.10),
согласно которому квадрат суммарной единичной эпюры МS равен сумме всех коэффициентов при неизвестных:
|
|
2 |
n n |
|
|
|
|
||||
Эп.МS |
ik . |
(6.10) |
|||
EJ |
|||||
i 1k 1 |
|
||||
В случае неудовлетворения равенства (6.10) осуществляют согласно выражению (6.11) построчную проверку, когда произведение суммарной
единичной эпюры MS на любую единичную эпюру должно дать сумму единичных перемещений того уравнения, на единичную эпюру которой осуществлялось перемножение:
|
|
|
|
|
n |
|
|
Эп.МS Эп.Мk |
|
||||||
ik . |
(6.11) |
||||||
|
|||||||
|
|
EJ |
|
|
k 1 |
|
|
Правильность определения свободных членов системы канонических уравнений метода сил осуществляется в соответствии с выражением (6.12). В соответствии с (6.12) суммарную единичную эпюру MS умножают на
74
грузовую эпюру MF0 . Результат этого умножения должен быть равен сумме свободных членов системы канонических уравнений:
Эп. |
|
|
Эп.М0 |
|
|
М |
S |
|
|||
|
|
F |
iF . |
(6.12) |
|
|
|
|
|
||
|
|
EJ |
|
||
После контроля правильности определения параметров системы канонических уравнений их подставляют в эту систему и тем или иным известным из линейной алгебры методом решают. В результате решения находят значения «лишних» неизвестных Хi .
6.5.Построение итоговых эпюр внутренних усилий
взаданной системе
Основная система, в которой определены значения всех «лишних» неизвестных, представляет собой статически определимую систему с действующими на неё заданной внешней нагрузкой и усилиями Хi .
Для построения эпюр внутренних усилий M, N, Q составляются аналитические выражения этих внутренних усилий для характерных участков рассчитываемой конструкции.
Кроме того, для построения эпюр внутренних усилий может быть использован также приём, основанный на принципе независимости действия сил. На основании этого принципа для заданной n раз статически неопределимой системы усилия определяются в соответствии с выражением
Эп.Митог Эп.МF0 Эп. |
|
i Xi . |
(6.13) |
M |
По полученным ординатам (6.13) строят эпюру Mитог .
Поперечные силы в заданной системе определяются по известной из теории изгиба дифференциальной зависимости
|
dM |
|
Mправ |
Млев |
|
|
|
Qх |
|
tg Qx0 |
|
|
|
, |
(6.14) |
|
|
|
|||||
|
d |
|
|
|
|
||
где угол между эпюрой M и осью стержня рамы; Qx0 балочное значение поперечной силы.
Продольные силы N в заданной системе определяют путём вырезания узлов на эпюре Qх . Составляют уравнения равновесия для этих узлов, проецируя силы на оси стержней, из которых и находят искомые значения
75
усилий N.
По эпюрам Mитог , Q, N определяют реактивные усилия в опорах рассчитываемой рамы и проводят две проверки правильности построения итоговых эпюр внутренних усилий.
Узловая проверка. Вырезая узлы на эпюре Mитог , составляют уравнения равновесия статики М , равенство нолю которых свидетельствуют о правильности построенной эпюры Mитог .
Статическая проверка. Для осуществления статической проверки показывают заданную схему рамы с действующей на неё заданной внешней нагрузкой и с отброшенными опорными связями, вместо которых поставлены усилия, снятые с эпюр Q и N. Рассматривая равновесие такой схемы рамы, составляют уравнения, представляющие собой суммы проекций всех сил на две взаимно-перпендикулярные оси. Равенство нолю этих уравнений свидетельствует о правильности построенных эпюр Q и N.
6.6.Расчёт статически неопределимых рам методом сил на температурные воздействия
Действие на конструкцию температуры является также действием внешнего силового фактора. При этом предполагается, что элементы конструкции работают в пределах упругих деформаций и поэтому действителен принцип независимости действия сил, что позволяет проводить расчёт отдельно как от действия обычных внешних нагрузок, так и от действия температур. В соответствии с этим канонические уравнения метода сил при расчёте на температурные воздействия имеют вид
X1 11 ... |
Xi 1i ... |
Xn 1n 1t 0; |
|
|
|
|
|
|
|
................................................................. |
|
|||
|
|
Xi ii |
Xn in it 0; |
(6.15) |
X1 i1 |
||||
................................................................ |
|
|||
|
|
|
|
|
|
|
Xi in |
Xn nn nt 0. |
|
X1 n1 |
|
|||
В системе уравнений коэффициенты при неизвестных (единичные перемещения) определяются так же, как при обычном расчёте, свободные члены it представляют собой перемещение в основной системе по направлению устранённой i-й связи от действия температуры. В результате решения системы уравнений (6.15) находят значения неизвестных усилий Хit. Тогда итоговая эпюра Mитогt может быть построена в соответствии с выражением
76

n |
|
Mитогt Mi Xit . |
(6.16) |
i 1
В основной системе от действия температуры возникают только перемещения, а внутренние усилия при этом равны нолю. В заданной системе возникают как перемещения, так и внутренние усилия.
Рассмотрим пример расчёта статически неопределимой рамы (рис. 6.4) в качестве внешней нагрузки на которую рассматривается действие изменения температуры.
Исходные данные для расчёта: =10м; α-коэффициент температур-
ного расширения; t1 температура наружных волокон рамы; t2 темпера-
тура внутренних волокон; t1 > t2 ; h = 0,125 высота поперечного сечения рамы (рис. 6.5).
t1 |
|
|
|
EJ |
|
t1 |
|
Заданная сис- |
h |
x |
|
ℓ |
|||
|
|||
t1 |
|
||
2EJ |
|
||
t2 |
|
t2 |
|
|
|
||
ℓ |
|
Рис. |
Рис. 6.4
Степень статической неопределимости заданной системы определится из выражения
n = 3К Ш = 3 2 4 = 2. |
(6.17) |
Из (6.17) очевидно, что заданная система является дважды статически неопределимой.
Основная система (рис. 6.6) выбрана из заданной путём устранения двух простых кинематических связей, составляющих шарнирно-неподвиж- ную опору. Для того чтобы основная система была эквивалентна заданной, вместо устранённых связей поставлены искомые усилия Х1t и Х2t.
В связи с тем, что при определении перемещений от действия температуры учитывается влияние и изгибающих моментов M, и продольных сил N, единичные эпюры построены для этих силовых факторов. На рис. 6.7 и 6.8 представлены эпюры от действия соответственно Х1 = 1 и Х2 = 1.
77

|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Эп. М1 |
|
|
|
|
|
|
Эп. N1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
ℓ |
. 6.7 |
|
1 |
|
|
вид |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис |
|
|
|
|
|
|
|||||||||
Система канонических уравнений для |
данной задачи принимает |
|
|||||||||||||||||||||||||
выражения |
|
|
Х |
|
|
|
X |
|
|
0; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
(6.18) |
||||||||||||||||||
|
|
|
|
|
|
11 |
|
1t |
|
12 |
|
|
|
2t |
|
|
|
1t |
0. |
||||||||
|
|
|
|
|
21 X1t |
22 X |
2t 2t |
|
|
|
|
||||||||||||||||
|
Х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основная система |
|
|
|
|
|
ℓ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
метода сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
х1=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2=1
_
Эп. М2
ℓ
-1 |
-1 |
|
_ |
Эп. N2 |
|
Рис. 6.8
78
Определим коэффициенты канонических уравнений:
|
|
Эп. |
|
|
|
|
Эп. |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
5 3 |
|
|||||||||||
11 |
М |
1 |
М |
1 |
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
6EJ |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
2EJ |
3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Эп. |
|
|
|
Эп. |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
М |
1 |
М |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
12 |
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
(6.19) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EJ |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4EJ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
Эп. |
|
|
|
Эп. |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
1 |
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||
|
|
22 |
|
М |
2 |
М |
2 |
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
6EJ |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЕJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EJ |
|
|
|
|
|
|
|
|||||||||||||||
Свободные члены системы уравнений (6.19) определим по формулам предыдущего раздела:
|
|
|
|
|
it |
t |
|
|
tср |
|
, |
(6.20) |
||||||||
|
|
|
|
|
|
M |
N |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||
где t t1 |
t2 |
изменение температур; h высота поперечного сечения |
||||||||||||||||||
элемента; |
|
8; t 300 |
С; t |
2 |
200 С; |
|
площадь эпюры моментов |
|||||||||||||
|
М |
|||||||||||||||||||
|
|
|
h |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
площадь эпюры продольных сил |
|
|
|
||||||||||
|
М |
i в основной системе; |
|
|
|
N |
i в ос- |
|||||||||||||
|
N |
|||||||||||||||||||
новной системе.
Знаки в (6.20) определяют, сравнивая деформации от температуры и от единичного воздействия. Если кривизна от силы и температуры и от одного знака, то знак в десятом слагаемом берётся плюс.
Если деформации от силы и от температуры одного знака, то второе слагаемое будет положительное.
|
t |
|
|
|
t 1 |
|
|
|
|
|
|
|
t |
|
(1 3 |
|
); |
|||||
1t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
2 |
|
h |
|||||||||||||||||
|
|
|
|
|
h 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2t |
t |
|
t |
|
1 |
|
t |
( |
|
1). |
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
h |
2 |
|
|
|
2 |
|
|
h |
|
|
|||
Подставляя найденные значения перемещений (6.19) и (6.20) в систему уравнений (6.18), получают систему уравнений
5 |
|
|
3 |
|
X |
|
|
|
3 |
|
X |
||
|
|
|
|
|
|
1t |
|
|
|
||||
6 |
EJ |
|
|
||||||||||
|
|
|
|
|
|
|
4EJ |
||||||
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
X |
1t |
|
|
|
X |
||
|
|
|
4EJ |
|
|
|
|
||||||
|
|
|
|
|
|
|
6EJ |
||||||
2t
2t
|
t |
|
|
|
|
|
|
0; |
|
|
|
|
1 3 |
|
|
|
|||
2 |
h |
||||||||
|
|
|
|
|
(6.21) |
||||
|
t |
|
|
|
|
||||
|
|
0. |
|||||||
|
|
|
1 |
|
|
|
|||
2 |
|
|
|
||||||
|
|
|
h |
|
|
||||
79
