
1711
.pdf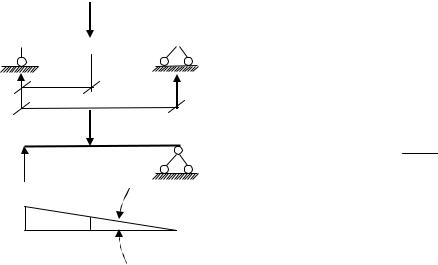
дых тел, связанная между собой идеальными связями, находится в равновесии, то сумма работ всех заданных сил на любых сколь угодно малых возможных перемещениях равна нулю.
Идеальными считаются такие связи, в которых отсутствуют трение, обмятия узлов и другие аналогичные явления. Возможными считаются такие перемещения, какие допускают идеальные связи.
В соответствии с этим методом каждая линия влияния представляет собой эпюру перемещений. Рассмотрим построение линии влияния опорной реакции (рис. 2.15) для однопролётной балки АВ. Поместив подвижную единичную силу F в произвольную точку, отбрасывают опорную связь в точке А.
Под действием силы F =1 балка АВ, ставшая механизмом, повернётся вокруг опоры В на угол , а перемещение точки под силой F=1 составит величину у.
В соответствии с принципом Лагранжа можно записать следующее выражение:
F у RA = 0. |
(2.9) |
Работа силы взята со знаком минус, так как сила RA противоположна направлению перемещения точки А. Учитывая то, что F =1, из (2.9) найдём RA = 1 у .
_
F=1
А 
 В
В
|
х |
|
RА |
ℓ |
RВ |
|
_ |
|
АF=
RА |
|
В |
|
|
|
||
y |
|
Л.в. RА |
|
|
|||
|
|
Если ординаты возможных перемещений выразить как функцию угловой скорости возможного вращения вокруг шарнира В, то выражение величины опорной реакции получит такой же вид, как и выражение (2.1),
т. е. RA = F x . Исходя из это-
го, когда подвижная сила F =1 будет находиться над опорой А, станет соблюдаться равенство
у= .
Рис. 2.15
При построении линии влияния момента для превращения балки АВ в механизм (рис. 2.16) в сечение, для которого требуется построить эту линию влияния, вводят условный шарнир. Высвободившееся усилие обозначают символом M. Введение шарнира даёт балке возможность провиснуть, и эпюра возможных перемещений такой балки охарактеризуется двумя
20

прямыми, взаимно пересекающимися на вертикали под шарниром. Восстановление равновесия может быть достигнуто приложением в рассматриваемом сечении двух равных взаимно противоположных моментов М.
Выражение возможной работы в этом случае примет следующий вид:
М М F y . |
(2.10) |
|
Учитывая то, что F=1, из (2.10) найдём М = |
1 у |
. |
|
||
Величины угловых смещений и по их малости могут быть заменены тангенсами, а именно к а, тогда последнее выражение примет вид:
М = |
у |
|
у |
а |
х |
. |
(2.11) |
|
|
|
|||||
|
|
к |
|
|
|||
К_
F=1
А |
В |
|
а |
М |
М |
|
|
|
|
|
|
|
α |
К |
y |
|
|
|
|
α |
|
|
|
Рис. 2.16
По выражению (2.11) можно найти ординаты линии влияния М. При построении линии влияния поперечной силы Q для превраще-
ния балки АВ в механизм (рис. 2.17) в сечение, в котором требуется построить эту линию влияния, вводят условное устройство, допускающее только взаимный сдвиг звеньев балки между собой.
|
|
_ |
|
А |
К |
F=1 |
В |
|
|||
|
|
|
|
|
|
|
|
а
21
ℓ
_
F=1
Выражение возможной работы в этом случае примет вид
Q c Q c′ + F y = 0.
Откуда с учётом того, что с +с′ = , находят
Q = |
у |
|
х |
. (2.12) |
|
|
|||
|
|
|||
2.8.Определение расчётного положения подвижной системы нагрузок
Расчётное положение подвижной системы сосредоточенных сил над линией влияния усилия S соответствует max или min искомой величины этого усилия. В общем случае искомое усилие S может иметь несколько экстремальных (max или min) значений.
Втех случаях, когда искомое усилие S=f(x), представляет собой функцию положения системы сил на балке, и её первая производная, являющаяся непрерывной функцией, из условия dS/dx = 0 можно найти положение подвижной системы сосредоточенных сил, при которых S=f(x) достигает экстремального значения.
Рассмотрим определение экстремального значения усилия S при загружении треугольных линий влияния.
Для случая, когда вершина треугольника линии влияния находится в начале или в конце линии влияния (рис. 2.18), экстремальным положение подвижной системы сосредоточенных нагрузок будет тогда, когда вся наибольшая нагрузка находится над вершиной линии влияния или вся система нагрузок находится над всей линией влияния, начиная с её вершины.
То или иное расположение нагрузки зависит от количественных значений каждой из нагрузок, составляющих данную подвижную систему.
Вслучае, когда подвижная нагрузка представляет собой равномерно распределённую нагрузку, экстремальным будет такое (рис. 2.19) расположение этой нагрузки, когда ординаты этой линии влияния, находящиеся
вначале и конце действия распределённой нагрузки ун и ук, будут равны
22

между собой.
F F F F |
q |
||
|
|||
|
|
|
|
|
|
|
|
Л.в. S
Л.в. S
yн yк
Рис. 2.18 Рис. 2.19
При загружении треугольной линии влияния системой сосредоточенных подвижных сил (рис. 2.20), когда вершина линии влияния находится на некотором расстоянии а от её начала, любое усилие можно найти исходя из выражения
n |
|
S Fi yi . |
(2.13) |
i 1 |
|
Если предположить, что вся система нагрузок сдвинулась вправо или влево, значение усилия получит приращение dS. В правой части равенства (2.13) ординаты изменятся на величину dx tg k. Тогда
|
n |
|
|
|
|
|
dS Fi |
tg idx. |
(2.14) |
||
|
i 1 |
|
|
|
|
F1 F2 |
Fi |
Fn |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
y2 |
yi |
α2 |
α1 |
|
|
a
Рис. 2.20
Сумма, стоящая в правой части равенства (2.14), представляет собой значение первой производной от величины S . Известно, что функция достигает своего экстремального значения, когда её первая производная равна
23
нолю. В соответствии с этим
dS |
n |
|
|
|
Fi tg i = 0. |
(2.15) |
|
dx |
|||
i 1 |
|
Но так как углы наклона 1, 2, …, k, …, n линии влияния остаются без изменения, выражение (2.15) может обратиться в ноль при условии, если изменяются величины некоторых сил F. Последнее условие возможно только при переходе какой-либо силы, называемой Fкр, через вершину линии влияния. Исходя из этого получены условия (2.16), определяющие экстремальное положение над треугольной линией влияния системы сосредоточенных подвижных нагрузок:
Fлев |
Fкр |
|
Fправ |
; |
||
|
|
|
|
|
||
a |
|
|
b |
|||
|
|
|
|
(2.16) |
||
Fлев |
|
Fправ Fкр |
|
|||
|
|
|
|
|
|
. |
a |
|
|
b |
|||
|
|
|
|
|
||
В практике расчёта конструкций транспортных сооружений часто используют так называемую эквивалентную нагрузку. Эквивалентной назы-
вается такая равномерно распределённая нагрузка интенсивностью qэ, которая создаёт в рассматриваемом сечении такое же усилие, какое вызывает система из сосредоточенных нагрузок, установленная в экстремальном положении.
При загружении линии влияния любого усилия системой сосредоточенных нагрузок усилие может быть найдено по выражению (2.6)
n
SF Fi yi . По данному определению эквивалентной нагрузки усилие в
i 1
соответствии с (2.7) может быть найдено по выражению S qэ . Приравнивая оба значения S, найдём
|
n |
|
|
|
|
Fi |
yi |
|
|
qэ |
i 1 |
|
. |
(2.17) |
|
|
|||
|
|
|
|
|
Очевидно, что величина эквивалентной нагрузки зависит от вида и очертания линии влияния. Однако для подобных между собой линий влияния, которые могут быть построены одна из другой изменением всех ординат в одном и том же соотношении, эквивалентные нагрузки имеют одинаковую интенсивность
2.9. Узловая передача нагрузки
24

В конструкциях транспортных сооружений внешняя, в частности под- |
|||||||||
вижная, нагрузка на несущие элементы передаётся через вспомогательные |
|||||||||
элементы. Имеет место так называемая узловая передача нагрузки. В этом |
|||||||||
случае обобщение закона о линиях влияния требует, чтобы последние в |
|||||||||
характере своего изменения удовлетворяли, с одной стороны, основному |
|||||||||
свойству линии влияния, по которому (рис. 2.21) усилие определяют по |
|||||||||
формуле SF F y; |
с другой стороны, чтобы эта величина удовлетворяла |
||||||||
условию |
передаточного |
действия |
нагрузки, |
по |
которому |
||||
S Fn yn Fn 1yn 1. |
|
|
|
|
|
_ |
|
||
|
|
|
|
|
|
|
|
|
|
По правилу рычага нагрузку F |
|
|
F=1 |
|
|||||
|
|
|
|
||||||
раскладывают |
на нагрузки |
Fn |
и |
n |
|
n+1 |
|
||
Fn+1, являющимися узловыми на- |
|
|
|||||||
Fn |
d |
Fn+1 |
|
||||||
грузками |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
F F d x; F |
F x . |
(2.18) |
|
|
|
|
|||
n |
d |
n 1 |
d |
|
|
yn |
y |
yn+1 |
Л.в. S |
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
Рис. 2.21 |
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
F=1 |
|
|
|
|
А |
|
а |
|
к |
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
ℓ - а |
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Левая прямая |
Правая прямая |
|
|
|
|||
|
1 |
|
|
|
Правая прямая |
|
|
|
|
|
|
|
|
|
-1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Левая прямая |
|
|
|
|
|
||
|
|
|
|
Рис. 2.22 |
|
|
|
|
|
Отсюда следует, что при узловой передаче нагрузки линия влияния из- |
|||||||||
25

меняется между узлами по закону прямой. На рис. 2.22 показаны примеры построения линий влияния при узловой передаче нагрузки.
2.10. Определение усилий в матричной форме
При решении многих задач строительной механики удобным оказывается использование матричного аппарата линейной алгебры.
На основании принципа суперпозиций запишем аналитические выражения для определения любых внутренних усилий S в различных сечениях стержня, подверженного действию системы сосредоточенных сил.
S1 s11 F1 ... |
s1i Fi ... |
s1k Fk ; |
|
||||||
.......... |
.......... |
.......... |
|
.......... |
.......... |
|
|
...... |
|
|
si1 F1 |
|
sii Fi |
sik Fk ; |
(2.19) |
||||
Si |
|||||||||
.......... |
.......... |
.......... |
|
.......... |
.......... |
|
|
........ |
|
|
sn1 F1 |
sni Fi |
|
snk Fk . |
|
||||
Sn |
|
|
|||||||
В выражении (2.19) |
sij i |
|
; j |
|
усилие в i-м сечении от дейст- |
||||
1,n |
1,k |
||||||||
вия силы Fj 1. В матричной форме эта система уравнений может быть записана в виде
|
|
|
|
|
|
S Ls |
F . |
(2.20) |
||
В |
выражении |
(2.20) |
вектор |
искомых усилий S S1...Si...Sn ; |
||||||
F F ...F |
j |
...F Т транспонированный вектор внешних нагрузок. |
|
|||||||
1 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
s11 . |
s1i . |
s1k |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
. . . . . |
|
|
|
|
||
|
Ls |
|
si1 . |
sii . |
sik |
|
|
матрица влияния усилия. |
(2.21) |
|
|
|
|
|
. . . . . |
|
|
|
|
||
|
|
|
|
sn1 . |
sni . |
snk |
|
|
|
|
Из выражения (2.21) видно, что элементами матрицы влияния являются ординаты линий влияния того усилия, матрица влияния которого строится.
При определении усилий в матричной форме любая задача решается шире, чем это имеет место при определении усилия с помощью линии влияния. В этом случае охватывается сразу несколько сечений рассматриваемой конструкции. Размер матрицы влияния Ls зависит от числа участков, на которые разбивают рассчитываемую конструкцию.
26

Рассмотрим, например, построение матрицы влияния Lm моментов. Для |
||||||||||||||
этого возьмём двухопорную шарнирно опёртую с обеих сторон балку (рис. |
||||||||||||||
2.23), разделённую на пять (n) равных по длине участков. Длина каждого |
||||||||||||||
участка d= |
. Если в точках 1,2,3,4 приложены какие-то сосредоточенные |
|||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы F, то изгибающий момент М в каждом из этих сечений определится в |
||||||||||||||
соответствии с (2.19) из выражений (2.21) |
|
|
|
|
|
|||||||||
M1 F1 m11 F2 m12 F3 m13 F4 m14; |
|
|
||||||||||||
M2 F1 m21 F2 m22 F3 m23 F4 m24; |
(2.22) |
|||||||||||||
M |
3 |
F m |
31 |
F m |
32 |
F m |
33 |
F m |
34 |
; |
||||
M |
1 |
|
2 |
|
3 |
4 |
. |
|
||||||
4 |
F m |
41 |
F m |
42 |
F m |
43 |
F m |
44 |
|
|||||
|
|
1 |
|
2 |
|
3 |
4 |
|
|
|||||
А |
|
|
1 |
|
|
2 |
|
|
3 |
|
4 |
|
|
В |
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
d |
|
|
d |
|
|
d |
|
d |
|
d |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
m11 |
|
m12 |
|
m13 |
|
m14 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Л.в. М1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m21 |
|
m22 |
|
m23 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
m24 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Л.в. М2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m31 |
|
m32 |
|
m33 |
|
m34 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Л.в. М3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m41 |
|
m42 |
|
m43 |
|
m44 |
|
|||
|
|
|
|
|
|
|
|
|
|
Л.в. М4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.23 |
|
|
|
|
|
||
В матричной форме выражения (2.22) примут вид M Lm F , где М |
||||||||||||||
вектор-столбец искомых моментов; |
F вектор-столбец внешних нагрузок. |
|||||||||||||
Из рис. 2.23 и выражений (2.22) ясно, что элементами матрицы влия- |
||||||||||||||
ния Lm являются ординаты линий влияния моментов М для каждого сече- |
||||||||||||||
27
ния соответственно. Для данного примера эта матрица примет следующий вид:
|
|
m11 |
m12 |
|
|
m13 |
|
m14 |
|
|
|
|
|
|
|
|
||||||||||||||||||
L |
|
m21 |
m22 |
|
|
m23 |
|
m24 |
|
|
матрица влияния моментов. |
|||||||||||||||||||||||
m |
|
m |
m |
|
|
m |
|
m |
34 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
31 |
|
|
32 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
m41 |
m42 |
|
|
m43 |
|
m44 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
4d |
3d |
|
|
2d |
1d |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
n |
|
|
|
n |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
4 |
3 |
2 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3d |
6d |
|
|
4d |
2d |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
d |
|
3 |
6 |
4 |
2 |
|
|
||||||||||||||||||||
L |
|
n |
|
|
|
n |
|
|
|
|
n |
|
|
n |
|
|
|
|
|
. |
(2.23) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
m |
|
2d 4d 6d 3d |
|
|
|
|
n |
2 4 6 |
3 |
|
|
|||||||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
||||||||||
|
|
1d |
2d |
|
|
3d |
4d |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из анализа структуры матрицы влияния Lm наблюдается закономерность в определении элементов матрицы влияния моментов. Исходя из этого любой элемент матрицы влияния моментов может быть определён по формулам.
При i j mij=(d/n) (n j); при i j mij=(d/h) (n i).
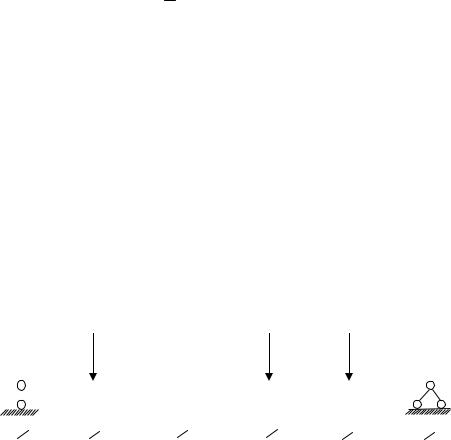
Рассмотрим пример построения эпюры М для балки (рис. 2.24), нагруженной системой сосредоточенных сил F.
Пролёт балки =10 м разделён на пять частей, т.е. n=5. Тогда длина
одной части составит d . F1 = 5кН; F2 = 15кН; F3 = 5кН. n
Построение эпюры М будем осуществлять в соответствии с выражением (2.19), которое в матричной форме имеет вид
M Lm F . |
(2.24) |
При этом вектор-столбец искомых моментов M , вектор-столбец F и матрица влияния моментов Lm приобретают следующий вид:
|
|
|
|
|
М1 |
|
|
F1 |
|
|
|
|
|
|
|
4 |
3 |
2 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
3 6 |
4 |
2 |
|
||||||
|
|
|
|
М |
M2 |
; |
F |
0 |
; |
|
|
L |
|
. |
|||||||||||
n |
6 |
||||||||||||||||||||||||
|
|
|
|
|
M3 |
|
|
F2 |
|
|
|
m |
|
2 |
4 |
3 |
|
||||||||
|
|
|
|
|
M4 |
|
|
F3 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
А |
|
F1 |
|
|
|
|
F2 |
|
|
|
F3 |
|
|
В |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
2 |
|
328 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
d |
|
|
d |
d |
|
|
|
d |
|
|
|
|
d |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя полученные матрицы в выражение (2.24) и совершая операцию перемножения матриц, получаем вектор-столбец искомых усилий изгибающих моментов М.
|
M1 |
|
4 |
3 |
2 |
1 |
|
5 |
|
22 |
|
|||
|
|
|
|
|
|
|
||||||||
|
2 |
3 |
6 |
4 |
2 |
|
|
|
||||||
M |
|
|
0 |
|
34 |
|
||||||||
M |
|
2 |
|
|
|
2 |
4 |
6 |
3 |
|
15 |
|
46 |
. |
|
|
|||||||||||||
|
M3 |
5 |
|
|
|
|||||||||
|
M4 |
|
|
|
1 |
2 |
3 |
4 |
|
5 |
|
28 |
|
|
|
|
|
|
|
|
|
|
|
||||||
По полученному вектору искомых изгибающих моментов построена эпюра М (см. рис. 2.24).
Матрицы влияния моментов для консольных балок имеют следующий вид:
|
|
|
0 |
1 |
2 . |
n |
|
|
|
|
|
|
0 |
0 |
1 . |
n 1 |
|
||
Защемление слева |
|
Lm d |
. . |
. . |
. |
|
. |
||
|
|
|
0 |
0 |
0 . |
1 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
. |
0 |
|
|
|
|
|
|
|||||
|
|
|
|
1 |
. |
0 |
0 |
0 |
|
Защемление справа |
|
Lm d |
|
. |
. . |
. . |
. |
||
|
|
|
n 1 |
. 1 0 |
0 |
|
|||
|
|
|
|
n |
. |
2 |
1 |
0 |
|
3. РАСЧЁТ РАСПОРНЫХ СИСТЕМ
29
