
1711
.pdf
3.1. Общие сведения
Распорной называется такая система, в результате действия на которую вертикальных внешних нагрузок в ней возникают наклонные опор-
ные реакции. На рис. 3.1 показаны два типа распорных систем.
F |
|
|
VА |
VА |
|
|
|
|
|
С |
HА |
|
|
HВ |
VА |
VВ |
А |
С |
В |
HА |
|
|||
|
|
|
|
|
А |
В |
|
F |
|
а |
|
|
б |
|
|
|
|
||
|
Рис. 3.1 |
|
|
|
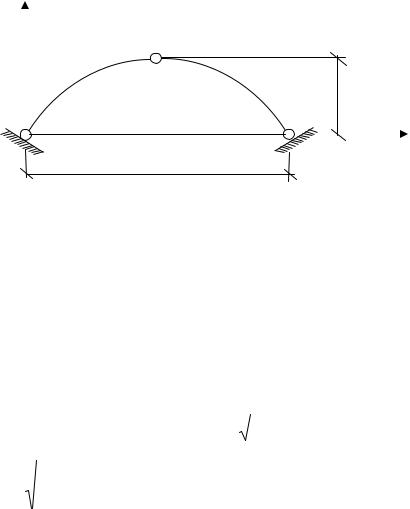
При расчёте распорных систем наклонную опорную реакцию R разлагают на две составляющие вертикальную V и горизонтальную Н. Горизонтальная составляющая опорной реакции Н называется распором. Если горизонтальная составляющая Н направлена вовнутрь конструкции, то такую конструкцию называют арочной системой (рис. 3.1, а), если наружу
висячей системой (рис. 3.1, б).
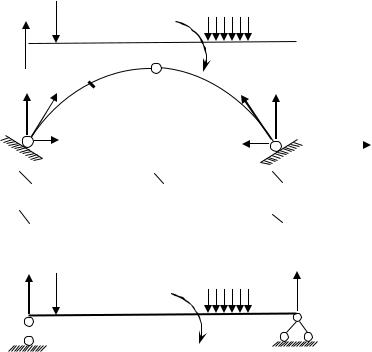
В настоящем курсе рассматривается только арочная система (арка). По степени статической определимости различают арки: трёхшарнир-
ные (рис. 3.2, а), двухшарнирные (рис. 3.2, б) и бесшарнирные (рис. 3.2, в).
а |
б |
в |
|
||
|
|
Рис. 3.2
Арки могут быть как сплошными, так и решётчатыми. Опоры арки могут располагаться как в одном уровне, так и в разных уровнях.
Конструктивные элементы арки показаны на рис. 3.3: пролёт арки; f стрела подъёма арки; шарниры А и В называются пятовыми, а шарнир Сзамковым. Элемент арки между шарнирами А и С называется левой полуаркой, а между шарнирами В и С правой полуаркой.
По отношению стрелы подъёма арки к её длине различают следующие
30
типы арок:
f |
|
1 |
подъёмистая арка; |
f |
|
1 |
пологая арка. |
|
|
|
|
||||
5 |
|
5 |
|
||||
y
С
f
А |
В |
х |
ℓ
Рис. 3.3
Ось арки может быть очерчена различными кривыми. Наиболее часто в практике транспортного строительства используется парабола, описанная выражением (3.1), и дуга окружности, описанная выражением (3.2).
|
|
|
|
|
|
y |
4 f |
x x парабола. |
(3.1) |
||||||
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тригонометрические функции, соответствующие параболе, имеют сле- |
|||||||||||||||
дующий вид: tg = |
4 f |
2x ; |
cos = |
|
1 |
|
; sin = cos tg . |
|
|||||||
2 |
|
|
|
|
|
||||||||||
|
1 tg2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
у R2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
|
R f |
|
дуга окружности. |
(3.2) |
|||||||
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Тригонометрические функции, соответствующие дуге окружности имеют
следующий вид: R |
f |
|
2 |
; |
sin |
2x |
; |
cos |
y R f |
. |
|
8f |
|
|
|||||||
2 |
|
|
|
2R |
|
R |
||||
В последних формулах R радиус окружности.
3.2. Расчёт трёхшарнирной арки на статическую нагрузку
Как и любой расчёт, расчёт трёхшарнирной арки начинают с определения опорных реакций. На рис. 3.4 изображена арка с пятами на одном уровне, находящаяся под воздействием системы внешних нагрузок.
Вертикальные составляющие Va и Vb опорных реакций Ra и Rb находят из рассмотрения пролёта арки, как пролёта балки. Тогда из МВ = 0 нахо-
31
дят:
VA |
MB0 |
|
|
|
|
|
|
M A0 |
|
|
|
|
, а из МА = 0 VB |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
q |
||
|
|
|
F |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
y |
|
|
|
|
|
|
|
|
||
|
|
|
К |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
RА |
|
|
RВ |
||||||
|
|
|
|
|
С |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
VВ |
|
|
|
VА |
|
|
|
|
|
|
||||
|
|
|
HА |
|
|
|
HВ |
|
|
x |
||
|
|
|
|
|
|
|
|
|
||||
|
А |
|
|
|
ℓ1 |
|
|
ℓ2 |
|
|
В |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
М |
q |
||||
|
|
|
|
|
VВ |
||||
VА |
К |
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.4
Здесь М А0 В представляет собой так называемый балочный момент,
т.е. момент, создаваемый вертикальными силами.
Для определения горизонтальных Нa и Нb составляющих опорных реакций Ra и Rb рассмотрим равновесие арки в целом, составив уравнение статики суммы проекции всех сил, действующих на арку, на горизонтальную ось х. х=Нa Нb = 0 Нa = Нb = Н. Далее, составляя уравнение моментов относительно замкового шарнира С, рассматривая при этом равновесие либо левой, либо правой полуарок, можно записать
Мсправ Мс0 прав Н f 0;
Мслев Мс0 лев Н f 0. |
|
(3.3) |
||||
|
|
|||||
Исходя из (3.3) находят Н |
Мс0 прав |
|
Mc0 лев |
. |
(3.4) |
|
f |
f |
|||||
|
|
|
|
|||
Для определения в произвольном сечении арки внутренних усилий
32

мысленно в этом сечении проводят плоскость, нормальную к оси арки (рис. 3.5). Положение плоскости определяется координатами её центра тяжести хк, ук и к.
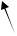 v
v
|
|
|
|
|
Nах |
|
|
|
Qах |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
φах |
|
К |
Мах |
||
y
yх
VА  HА
HА
Ах
Рис. 3.5
Отделяемая этим сечением любая из частей арки находится в равновесии под действием приложенных к рассматриваемой части арки внешних сил и равнодействующей R внутренних сил, приложенной к плоскости сечения. С отнесением равнодействующей R в центр тяжести сечения внутренние усилия в сечении арки будут определяться изгибающим моментом Мх, поперечной силой Qx и продольной силой Nx. Рассматривая равновесие оставшейся части арки (см. рис. 3.5), составляют уравнение моментов относительно сечения к и уравнения проекций всех сил на нормаль и касательную к оси арки в точке к соответственно. Исходя из этого получены выражения
M xa Mx0 |
H yx ; |
|
(3.5) |
Qxa Qx0 cos k |
H sin k ; |
|
(3.6) |
Nxa Qx0 sin k + H cos k |
|
(3.7) |
|
По приведённым формулам строят эпюры внутренних усилий, предва-
33
рительно определив геометрические параметры каждого рассматриваемого сечения трёхшарнирной арки.
3.3. Расчёт трёхшарнирной арки на подвижную нагрузку
Расчёт на подвижную нагрузку предполагает построение линий влияния всех искомых параметров, определяющих напряжённо-деформирован- ное состояние рассчитываемой конструкции.
Как обычно, расчёт начинают с построения линий влияния опорных реакций. Линии влияния вертикальных Va и Vb составляющих опорных реакций (рис. 3.6) строят в точности так же, как строят линии влияния опорных реакций в двухопорной без консолей балке. При этом пролёт арки рассматривается как пролёт балки с длиной пролёта, равной расстоянию между пятовыми шарнирами А и В.
Линия влияния горизонтальной (распора Н) составляющей опорной реакции может быть построена в соответствии с выражением (3.4), согласно которому
Л.в. Н |
Л.в.М0 |
|
|
с |
. |
(3.8) |
|
|
|||
|
f |
|
|
Из (3.8) видно, что линия влияния распора имеет в точности такой же вид, что и линия влияния изгибающего момента для сечения С, построенного из рассмотрения пролёта арки как пролёта простой двухопорной балки (см. рис. 3.5). В соответствии с этим все ординаты данной линии влияния поделены на постоянную f , равную стреле подъёма арки.
Линия влияния изгибающего момента Мка в произвольном сечении к арки, находящемся на расстоянии х от левой опоры, может быть построена исходя из формулы (3.5):
Л.в. Мка Л.в. Мк0 Л.в. |
Н ук . |
(3.9) |
В соответствии с этим выражением л.в. Мка представляет собой ал-
гебраическую сумму двух линий влияния линии влияния балочного момента и линии влияния распора Н, ординаты которой умножают на постоянную величину ук. На рис. 3.7, а показано построение Мка путём геометрического (метода наложений) сложения указанных линий влияния. На рис. 3.7, б показано построение л.в. Мка на базовой линии как результат алгебраического сложения двух разнозначных линий влияния.
Построение линии влияния поперечной силы Q основывается на фор-
34

муле (3.6) и соответствует выражению |
|
|
|
|
|
|
||
Л.в. Qa Л.в. Q0 |
cos |
k |
Л.в. Н sin |
k |
. |
(3.10) |
||
k |
k |
|
|
|
|
|
||
|
|
_ |
|
|
|
|
|
|
|
|
F=1 |
|
|
|
|
|
|
VА |
|
С |
|
|
VВ |
f |
||
|
|
|
|
|
||||
HА |
|
|
|
HВ |
|
|
|
|
А |
|
|
|
|
В |
|
|
|
ℓ1 |
|
|
|
ℓ2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
_ |
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
F=1 |
|
|
|
В |
|
||
|
|
|
|
|
||||
VА |
|
|
|
VВ |
|
|
|
|
1 |
|
|
|
|
|
|
Л.в. VА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л.в. VВ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Л.в. Н |
|
ℓ1 ℓ2 |
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
Рис. 3.6 |
|
|
|
|
|
||
Согласно (3.10) л.в. Qka |
представляет собой геометрическую сумму |
|||||||
двух линий влияния балочной линии влияния Q0 |
, построенной для сече- |
|||||||
|
|
|
|
k |
|
|
|
|
ния к из рассмотрения пролёта арки как пролёта балки, и линии влияния |
||||||||
35

распора Н , умноженных соответственно на значения cos k и sin k ,
имеющих место в сечении к. На рис. 3.8 показано построение л.в. Qka так называемым методом наложения. Как и в предыдущем случае, на базовой линии (рис. 3.8, б) показано сложение двух линий влияния.
Построение линии влияния продольной силы Nka , согласно формуле (3.7), можно осуществить по выражению
Л.в. Na |
|
Л.в. Q0 |
sin |
k |
Л.в. H cos |
. |
(3.11) |
k |
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
На рис. 3.9 показано построение этой линии влияния.
RВ |
_ |
RА |
|
F= |
|||
|
|||
К |
С |
f |
|
А |
|||
|
|
||
а |
ℓ1 |
ℓ2 |
|
|
|||
um |
|
ℓ- um |
|
|
|
ℓ |
|
|
Л.в. М0к |
|
|
а |
|
Л.в. Н-yк |
|
|
|
||
б |
|
|
|
|
|
Л.в. Мак |
|
|
Рис. 3.7 |
|
Анализ всех трёх линий влияния показывает, что на каждой из них есть
36

такая точка, при положении над которой единичной подвижной силы ис- |
|||||||
комое усилие равно нулю. Эта точка называется нулевой и может быть ис- |
|||||||
пользована для геометрического построения указанных линий влияния. |
|||||||
При использовании геометрического метода нулевых точек для получения |
|||||||
аналитических значений ординат этих линий влияния необходимо знать |
|||||||
расстояния UM, UQ и UN соответственно. Эти расстояния можно найти из |
|||||||
рассмотрения подобия соответствующих треугольников, получившихся в |
|||||||
процессе построения линий влияния. |
|
|
|
|
|
|
|
На рис. 3.6, 3.7 и 3.8 показаны эти треугольники, из подобия которых |
|||||||
получены следующие формулы: |
|
|
|
f |
|
|
|
Для л.в. Мка |
|
UM |
|
. |
(3.12) |
||
|
|
|
|
||||
|
|
|
|
f |
|
|
|
|
|
2 |
yk |
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
RВ |
_ |
RА |
|
|
|
|
|
F=1 |
|
|
|
|
|||
К |
С |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
А |
φк |
|
|
|
|
|
|
|
|
|
|
|
|
||
а |
ℓ1 |
ℓ2 |
|
|
В |
|
|
|
|
|
|
|
|
||
|
uQ |
ℓ- uQ |
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
а |
Л.в. Q0к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos φк |
|
Л.в. Н-yк |
|
|
|
||
б |
|
|
|
|
|
|
|
cos φк |
|
|
|
|
Л.в. Qак |
|
|
|
|
|
|
|
|
||
|
Рис. 3.8 |
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|

Для л.в. Qka |
UQ |
tg |
|
; |
tg |
f . |
(3.13) |
||
|
|
tg k |
tg |
|
|
2 |
|
||
D |
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
F=1 |
|
|
|
|
|
|
|
|
|
RА |
К |
|
|
|
|
|
|
RВ |
|
|
|
|
|
С |
|
f |
|||
|
|
φк |
|
|
|
||||
|
|
|
|
|
|
|
|
||
А |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
||
uN |
|
ℓ1 |
|
|
|
|
ℓ2 |
|
|
|
|
|
|
|
|
|
|||
|
|
ℓ |
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
Л.в. Q0к sin |
|
|
sin φк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л.в. Н cos φк |
|
|
sin φк |
|
|
|
|
|
|
|
Л.в. Nак |
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.9 |
|
|
|
||||
Для л.в. Nka |
|
UN |
|
|
tg . |
(3.14) |
|||
|
|
|
|
ctg k tg |
|
|
|||
В случае расположения сечения к на правой полуарке формулы (3.12), (3.13) и (3.14) можно использовать с учётом того, что эти расстоя-
38

ния необходимо отмерять от правой пятовой опоры В. |
||||
|
к1 |
|
|
|
А |
RА |
|
RВ |
f |
|
|
|||
φк |
_ |
|
В |
|
|
|
F=1 |
|
|
cos φк |
|
|
|
|
|
|
|
|
Л.в. Qак |
|
uQ |
|
|
|
|
Рис. 3.10 |
|
|
|
|
|
_ |
|
|
|
RВ |
F=1 |
|
|
|
RА |
|
|
|
|
|
|
|
|
|
к1 |
|
|
|
|
φк |
|
|
f |
|
|
|
|
|
cos φк |
|
|
|
|
Л.в. Qак
uQ
Рис. 3.11
Рассмотрим два частных случая построения л.в. Qka , показанных на
39
