
- •Введение
- •Раздел 1. ОПРЕДЕЛЕНИЕ ЭКОНОМЕТРИКИ
- •1.1. Предмет эконометрики
- •1.2. Особенности эконометрического метода
- •1.3. Виды измерений
- •Раздел 2. ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
- •2.1. Спецификация модели
- •2.2. Линейная регрессия и корреляция
- •2.4. Интервальный прогноз на основе линейного уравнения регрессии
- •2.5. Нелинейная регрессия
- •2.6. Подбор линеаризующего преобразования
- •2.7. Корреляция для нелинейной регрессии
- •2.8. Средняя ошибка аппроксимации
- •Раздел 3. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
- •3.4. Оценка параметров уравнения множественной регрессии
- •3.5. Частные уравнения регрессии
- •3.7. Частная корреляция
- •3.8. Оценка надежности результатов множественной регрессии и корреляции
- •3.9. Фиктивные переменные во множественной регрессии
- •3.10. Предпосылки метода наименьших квадратов
- •3.11. Обобщенный метод наименьших квадратов
- •РАЗДЕЛ 4. ГЕТЕРОСКЕДАСТИЧНОСТЬ
- •РАЗДЕЛ 5. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- •5.1. Общие понятия о системах уравнений
- •5.2. Структурная и приведенная форма модели
- •6.1. Основные элементы временного ряда
- •6.2. Автокорреляция уровней временного ряда и выявление его структуры
- •6.3. Моделирование тенденций временного ряда
- •6.4. Моделирование сезонных и циклических колебаний
- •Перечень вопросов для подготовки к экзамену (зачету)
- •Библиографический список
Раздел 2. ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
2.1. Спецификация модели (презентация 2)
Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующих связей СибАДИмежду переменными. Рассматривая зависимости между признаками, необходимо выдел ть прежде всего две категории зависимости: функциональные и
корреляц онные.
Функц ональные связи характеризуются полным соответствием между изменен ем факторного признака и изменением результативной величины, и каждому значен ю пр знака-фактора соответствуют вполне определенные значения результат вного признака. Функциональная зависимость может связывать результат вный признак с одним или несколькими факторными признаками.
В корреляц онных связях между изменением факторного и результативного пр знака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.
Регрессией в теории вероятностей и математической статистике принято называть зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин (х). В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) множественную регрессию.
Парной регрессией называется модель, выражающая зависимость среднего значения зависимой переменной y от одной независимой переменной х:
|
|
|
; |
(1) |
где у – зависимая |
переменная (результативный признак); |
|
||
|
= |
( ) |
|
|
х – независимая, объясняющая переменная (признак-фактор). |
|
|||
Практически в каждом отдельном случае величина y складывается из |
||||
двух слагаемых: |
= |
+ или |
= + ∙ + , |
|
|
(2) |
|||
13
где y |
– фактическое значение результативного признака; |
|
|
|
||||||||||||
|
– теоретическое |
значение |
|
результативного |
признака, |
найденное |
||||||||||
исходя |
из уравнения регрессии; |
|
|
|
|
|
|
|
|
|||||||
|
– случайная величина, характеризующая отклонения реального значе- |
|||||||||||||||
ния |
результативного |
признака |
от теоретического, найденного |
по |
||||||||||||
уравнению регрессии. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Парная регрессия применяется, если имеется доминирующий фактор, |
|||||||||||||||
СибАДИ |
||||||||||||||||
обуславливающий большую долю изменения изучаемой объясняемой пере- |
||||||||||||||||
менной, |
который |
спользуется в качестве объясняющей переменной. Уравне- |
||||||||||||||
ние простой регресс |
|
характеризует связь между двумя переменными, |
кото- |
|||||||||||||
рая проявляется |
|
как |
некоторая закономерность |
лишь в среднем по совокуп- |
||||||||||||
ности наблюден й [1]. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
лучайная вел ч на |
включает влияние не учтенных в модели факто- |
||||||||||||||
ров, случайных ош |
ок |
осо енностей измерения. Её присутствие в модели |
||||||||||||||
порождено тремя |
сточн ками: спецификацией модели, выборочным характе- |
|||||||||||||||
ром исходных данных, осо енностями измерения переменных. |
|
|
|
|||||||||||||
|
От прав льно вы ранной спецификации модели зависит величина |
|||||||||||||||
случайных ош бок: они тем меньше, чем в большей мере теоретические |
||||||||||||||||
значения результативного признака |
, подходят к фактическим данным y. |
|
||||||||||||||
|
К ошибкам спецификации относятся неправильный выбор той или |
|||||||||||||||
иной |
математической функции для |
|
недоучет в уравнении регрессии ка- |
|||||||||||||
кого-либо существенного фактора, т.е. использование парной регрессии |
||||||||||||||||
вместо множественной. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Наряду с ошибками спецификации могут иметь место ошибки выборки, |
|||||||||||||||
которые |
имеют |
место |
в силу |
неоднородности |
данных |
в |
исходной |
|||||||||
статистической |
|
совокупности, |
что, |
как |
правило, |
бывает |
при |
изучении |
||||||||
экономических процессов. Если совокупность неоднородна, то уравнение |
||||||||||||||||
регрессии не |
имеет |
практического |
смысла. |
ля получения |
хорошего |
|||||||||||
результата обычно исключают из совокупности единицы с аномальными |
||||||||||||||||
значениями исследуемых признаков. |
|
|
|
|
|
|
|
|||||||||
|
Наибольшую |
|
опасность |
в |
практическом |
использовании |
мето- |
|||||||||
дов регрессии представляют ошибки измерения. Если ошибки специфика- |
||||||||||||||||
ции можно уменьшить, изменяя форму модели (вид математической форму- |
||||||||||||||||
лы), а ошибки |
выборки, |
– увеличивая |
объем |
исходных |
данных, то |
|||||||||||
ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.
14
По виду аналитической зависимости различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением
=+ ∙ + .
Примеры наиболее часто используемых уравнений нелинейной регрес-
сии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полиномы разных степеней |
|
|
|
|
|
|
|
|
|||||
СибАДИ∙ ∙ ̅ (4) |
||||||||||||||
|
равносторонняя гипербола |
|
= |
+ |
|
+ |
,+ |
+ |
+ , |
|||||
|
степенная |
|
[4]. |
|
|
|
= |
+ |
|
|
|
|
||
|
Для выбора =в да аналитической зависимости можно использовать сле- |
|||||||||||||
дующие методы: |
|
|
|
|
|
|
|
|
|
|
|
|
||
граф ческ й – в д зависимости определяется на основе анализа поля |
||||||||||||||
корреляц й; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анал т ческ й – на основе качественного анализа изучаемой взаимосвязи; |
|||||||||||||
|
экспер ментальный – построение нескольких моделей различного вида с |
|||||||||||||
выбором на лучшей согласно применяемому критерию качества [1]. |
||||||||||||||
|
|
|
|
2.2. Линейная регрессия и корреляция |
|
|||||||||
|
Линейная регрессия сводится к нахождению уравнения вида: |
|||||||||||||
|
|
|
|
= |
+ |
|
|
или |
|
|
|
|
||
|
Уравнение вида |
|
позволяет по заданным значениям факто- |
|||||||||||
|
|
∙ |
|
|
= + |
∙ + . |
|
|||||||
ра х находить |
теоретические значения результативного признака, подставляя в |
|||||||||||||
|
|
= |
+ |
∙ |
|
|
|
|
|
|
|
|||
него фактическое значение фактора х. |
|
|
|
|
|
|
||||||||
|
Классическим |
подходом для оценки параметров является метод наи- |
||||||||||||
меньших квадратов: |
a= |
|
− |
|
; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(3) |
|||
|
Параметр b |
называется коэффициентом корреляции, его величина показы- |
||||||||||||
|
|
= |
|
|
|
̅. |
|
|
|
|
||||
вает среднее изменение результата с изменением фактора х на одну единицу. Значение a – значение y при х=0.
15
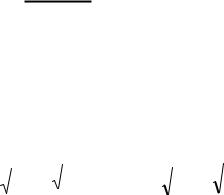
Тесноту связи изучаемых явлений оценивает линейный коэффициент корреляции:
|
|
|
|
|
|
|
= |
|
∙ |
∙ |
∙ |
̅ |
|
|
|
|
|
|
|
|
|
|
(5) |
||||
где |
|
x |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
– среднее значение переменной x (выборочное среднее); |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДИ |
||||||||||
|
y – среднее значение переменной y (выборочное среднее); |
|
|
||||||||||||||||||||||||
|
|
x y |
– среднее значение произведений; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
х |
|
y – выборочные средние квадратичные отклонения переменных х и y: |
||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
x2 |
|
|
x2 |
- |
x |
2 ; y |
y2 |
|
|
y2 |
- |
y |
2 . |
|
|
(6) |
|||
Коэффиц ент корреляц |
зменяется в диапазоне от |
|
|
|
|
|
|
. Чем ближе |
|||||||||||||||||||
абсолютное значен е |
к единице, |
тем сильнее |
линейная связь между фак- |
||||||||||||||||||||||||
|
−1 ≤ |
≤ 1 |
|
|
|||||||||||||||||||||||
торами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Для оценки качества под ора линейного уравнения регрессии исполь- |
||||||||||||||||||||||||||
зуют коэфф ц ент детерм нации |
( |
2 |
) |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||
|
Коэффициент |
детерминации характеризует долю дисперсии результа- |
|||||||||||||||||||||||||
|
= ( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
тивного признака, объясненную с помощью уравнения регрессии. Значение |
|||||||||||||||||||||||||||
коэффициента изменяются от нуля до единицы: в пределах |
|
|
. [1,4]. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корреляции |
||
2.3. Оценка значимости параметров линейной регрессии0и≤ |
≤ 1 |
|
|||||||||||||||||||||||||
|
Проверка значимости уравнения линейной регрессии предполагает |
||||||||||||||||||||||||||
оценку значимости как уравнения в целом, так |
отдельных его параметров. |
||||||||||||||||||||||||||
|
Оценка значимости |
уравнения регрессии в целом осуществляется с по- |
|||||||||||||||||||||||||
мощью F- критерия Фишера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
F- критерий Фишера рассчитывается по формуле: |
|
|
|
|||||||||||||||||||||||
СибАфакт |
|
|
|
|
|
|
|
|
(8) |
||||||||||||||||||
где F-критерий для проверки=нулевойост , |
гипотезы |
факт = ост; |
|
|
|
||||||||||||||||||||||
|
факт – факторная дисперсия |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
16
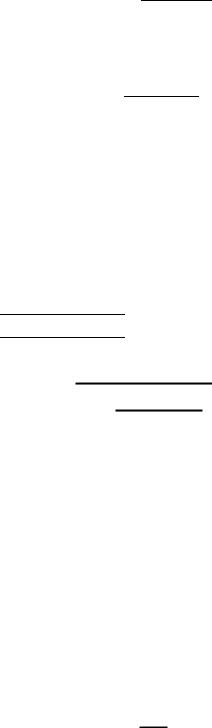
ост |
– остаточная дисперсияфакт = |
∑( |
) |
; |
(9) |
||
ост |
∑( |
) |
. |
|
(10) |
||
|
|
||||||
СибА= . ДИ(16) |
||||||||||||||||||||
|
|
Рассчитанное |
значение |
F- отношений признается достоверным, если |
||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
||||||||||
оно больше табличного, |
т. е связь между признаками существенна: |
|
||||||||||||||||||
|
. Если |
|
|
|
|
, то уравнение регрессии считается |
статистически не- |
|||||||||||||
табл |
|
|
|
факт |
< |
|
табл |
|
|
|
|
|
|
|
|
|
|
|
|
|
значимым. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Для оценки знач мости |
параметров уравнения регрессии, а также ко- |
|||||||||||||||||
эффициента корреляц |
|
рассчитывается стандартная ошибка по каждому па- |
||||||||||||||||||
раметру: |
|
|
∑( |
|
) /( |
) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
= |
|
|
∑( |
|
̅) |
|
|
= |
∑( |
|
̅) ; |
|
|
|||
|
|
|
|
|
|
|
= |
|
|
∙ |
∙∑∑( |
̅) |
; |
|
|
(12) |
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где S |
– остаточная |
дисперсия на одну степень свободы. |
ля оценки сущест- |
|||||||||||||||||
|
|
= |
|
|
|
|
, |
|
|
|
|
|
|
|||||||
венности коэффициента регрессии рассчитывается t-критерий Стьюдента: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
; |
|
|
|
(14) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
; |
|
|
|
(15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Фактическое значение критерия Стьюдента сравнивается с табличным при определенном уровне надежности α и числе степеней свободы df = n-2. Если фактическое значение критерия Стьюдента больше табличного, гипотеза о несущественности связи отвергается, что свидетельствует о существенности уравнения регрессии в целом [1,7].
17
