Белозеров В.И., Жук М.М., Кузина Ю.А., Терновых М.Ю. Физика и эксплуатационные режимы реактора ВВЭР-1000

Вследствие испускания α-частицы заряд ядра уменьшается на две единицы, а массовое число – на четыре единицы. Пример α- распада:

Учитывая в уравнении (1.12.1), что та = mα и Z – Z1 = 2, получится энергетическое условие α-распада. Заменив ma + 2me величи-

Так как энергия Wр > 0, то α-распад возможен в том случае, когда масса материнского ядра больше суммы масс дочернего ядра и

ядра гелия 42 He. В последнем примере масса 238U превышает сум-

марную массу 23490 Th и 42 He на М = 0,0045 а.е.м.

Процесс α-распада имеет две особенности, которые были найдены на основе экспериментального изучения α-распада.

1. Постоянная распада λ и энергия α-частиц Еа связаны законом

Для всех семейств постоянная В1 одна и та же, а постоянная B2 изменяется от семейства к семейству. Закон Гейгера–Неттола показывает, что чем короче время жизни α-излучателя, тем больше энергия α-частицы.

Энергия α-частиц, покидающих ядра различных α-излучателей, меняется в пределах 4÷9 МэВ. Она значительно меньше энергии, которую α-частицы должны бы получить после α-распада при ускорении в электрическом поле ядра. Например, в α-распаде:

23892 U → 23490Th

потенциальная энергия отталкивания α-частицы на границе ядра тория составляет около 30 МэВ. Следовательно, α-частица после преодоления потенциального барьера должна ускориться не менее чем до 30 МэВ. Однако экспериментально наблюдаются только α- частицы с энергией 4,2 МэВ.

Как объяснить закон Гейгера–Неттола? Почему энергия испускаемых α-частиц сравнительно невысока? Ответы на эти вопросы

41

дает квантовая механика. Перед началом α-распада во многих ядрах уже существует по одной α-частице. Она движется с энергией Eα′ . Если бы не было потенциального барьера, α-частица выходила

бы из ядра с энергией Eα = Eα′ −V0 (рис. 1.10), где V0 – глубина по-

тенциальной ямы. Как раз такая энергия α-частиц и наблюдается экспериментально. Покидая ядро, α-частица как бы не замечает существование потенциального барьера.

Согласно законам квантовой механики α-частицам присущи волновые свойства. Поэтому при попадании на стенку потенциального барьера они отражаются от нее, как волны. Однако от стенки отражаются не все α- частицы. Часть их проникает сквозь стенку и уходит из радиоактивных ядер с энергией Eα. Эффект просачивания α-частиц через потенциальный барьер при энергиях ниже его высоты называют туннельным эффектом. Им объясняется причина низких энергий α-частиц в α-распаде.

С ростом энергии Eα′ уменьшается ширина потенциального барьера (см. рис. 1.10). Чем уже потенциальный барьер, тем больше вероятность выхода α-частицы из ядра. Таково физическое объяснение закона Гейгера–Неттола.

Долю столкновений α-частиц с потенциальным барьером, приводящих к α-распаду, называют коэффициентом прозрачности D. С увеличением энергии α-частицы коэффициент прозрачности растет и становится равным единице при энергиях Eα, больших высоты потенциального барьера V k.

При внешнем облучении ядра α-частицами или другими заряженными частицами с энергиями Eα < V k коэффициент прозрачности показывает долю частиц, проникающих в ядро через потенциальный барьер. Эти частицы вступают во взаимодействие с ядром, вызывая ядерные превращения.

42

Энергия α-частиц зависит от энергетического состояния дочернего ядра после α-распада. Если дочернее ядро образуется только в основном состоянии, то испускаются моноэнергетические α- частицы. Если же дочернее ядро образуется как в основном, так и в возбужденных состояниях, то испускаются несколько энергетических групп α-частиц и γ-кванты. Следовательно, спектр α-частиц

дискретный. В α-распаде 23592 U наблюдается три группы α-частиц с энергиями 4,559; 4,370 и 4,170 МэВ.

Дочерние ядра 23190 Th образуются в основном состоянии и на двух возбужденных уровнях. Дальнейший переход тория из возбужденного состояния в основное сопровождается излучением γ- квантов.

1.13.Бета-распад

Вβ-распаде происходит превращение одних изобаров в другие. Одна из особенностей β-распада – это сплошной энергетический

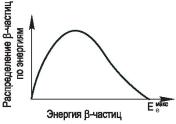
спектр β-частиц f(Ее) (рис. 1.11). Энергия β-частиц изменяется от нуля до энергии распада, которую называют максимальной (гра-

ничной) энергией Eeмакс . Кроме пози-

трона (электрона), в β-распаде испускается нейтрино ν (антинейтрино ν ). Оно характеризуется спином h/2, движется, как и γ-квант, со скоростью света, не имеет массы покоя и заряда. Нейтрино обладает огромной прони-

кающей способностью, поэтому заре- Рис. 1.11. Энергетический спектр гистрировать его очень трудно.

Энергия β-частицы Ee = Eeмакс − Eν . Она зависит от энергии Eν, уносимой нейтрино, что и является причиной сплошного спектра β-частиц. В среднем с β-частицами освобождается 1/3 Eeмакс , которая измеряется в эксперименте. Такое кажущееся нарушение закона сохранения энергии в β-распаде вызвало в свое время сомнения в применимости этого закона для микромира. В 1933 г. швейцар-

43

ский физик Паули теоретически обосновал испускание нейтрино и закон сохранения энергии в β-распаде.

По современной теории испускание β-частиц и нейтрино (антинейтрино) в β-распаде связано с превращением нуклонов в ядре. Электроны и позитроны возникают в процессе превращения нейтрона в протон или протона в нейтрон.

Если ядро содержит избыток нейтронов по сравнению со стабильным ядром с тем же порядковым номером Z, то происходит β- распад, в котором нейтрон в ядре заменяется протоном:

Порядковый номер ядра увеличивается на единицу, а массовое число остается постоянным. Энергия β–-распада находится из уравнения

Энергия распада Wp – положительная величина. Поэтому β- распад возможен только тогда, когда масса материнского атома М(Z,А) больше массы дочернего атома М(Z + 1,А).

Если ядро содержит избыток протонов, то его состав изменяется

Такое превращение протона в нейтрон может происходить только в ядре. В свободном состоянии протон – стабильная частица. Массовое число при β+-распаде не изменяется, а заряд ядра уменьшается на единицу. Энергетическое условие β+-распада отличается по записи от β–-распада [1]:

Wp = M(Z,A) – M(Z – 1,A) – 2me. (1.13.4)

Позитронный распад наблюдается в тех случаях, когда масса материнского атома больше массы дочернего атома не менее, чем на две электронные массы.

Последний, третий тип β-распада называют электронным захватом. Материнское ядро с избытком протонов захватывает орбитальный электрон из атомных оболочек. После захвата электрона, как и в позитронном распаде, один протон в ядре превращается в нейтрон:

Электронный захват обозначают так же, как и оболочку. Так, захват электрона с K-оболочки называют K-захватом, с L-оболочки

– L-захватом и т.д., а электроны, участвующие в этих процессах,

обозначают eK и eL и т. д.

В электронном захвате порядковый номер уменьшается на единицу (Z – Z1 = +1), а один электрон исчезает, поэтому энергия распада по уравнению (1.13.5):

где индекс n = K, L и т. д. – обозначение атомных оболочек. Следовательно, электронный захват может наблюдаться у материнского атома, масса которого больше массы дочернего атома. Уравнение электронного захвата

Над стрелкой, указывающей радиоактивный распад, записывают обозначение оболочки, с которой захватывается электрон. Пример K-захвата:

Энергия K-захвата WpK = 0,864 МэВ.

1.14. Пробег тяжелых заряженных частиц в веществе

Заряженная частица проходит в веществе некоторое расстояние, прежде чем потеряет всю кинетическую энергию. Полный путь заряженной частицы в веществе до остановки называют ее линейным пробегом R. Линейный пробег определяется удельными потерями энергии. Чем больше плотность атомных электронов и заряд частицы, тем выше эти потери и тем меньше пробег частицы в веществе. Тяжелые заряженные частицы, взаимодействующие в основном с атомными электронами, мало отклоняются от направления своего первоначального движения. Поэтому пробег тяжелой частицы измеряют расстоянием по прямой от источника частиц до точки ее остановки.

Хорошей иллюстрацией торможения α-частиц в воздухе служит кривая (рис. 1.12), которую получил в 1905 г. английский физик Брэгг для моноэнергетических α-частиц с начальной энергией 7,68 МэВ. С удалением частиц от источника удельная ионизация

45

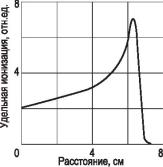
сначала медленно растет, а затем резко увеличивается и так же резко падает. Характер хода кривой объясняется изменением скорости α-частиц. Сначала α-частицы движутся с большой скоростью, поэтому удельная ионизация сравнительно небольшая. В результате ионизационных потерь движение α- частиц замедляется. Они проводят больше времени около электронов, и удельная ионизация растет. В конце своего движения α-частицы особенно интенсивно теряют энергию на иониза-

цию. Однако, медленно двигаясь, они захватывают сначала один орбитальный электрон, а затем второй и последовательно превращаются в однократно заряженные ионы гелия и атомы гелия. Поэтому ионизационные потери резко уменьшаются.

Плотность потока α-частиц практически не изменяется на расстоянии их пробега от источника, а интенсивность α-частиц уменьшается с увеличением расстояния от источника вследствие потерь энергии на ионизацию.

Взаимодействие α-частиц с электронами имеет вероятностный характер. Поэтому пробеги α-частиц в веществе имеют некоторый разброс. Незначительная часть α-частиц проникает дальше других от источника. Средний пробег Rα моноэнергетических α-частиц рассчитывают по эмпирическим формулам.

В воздухе при нормальных условиях:

где Rα – пробег, см; Eαn – кинетическая энергия α-частиц, МэВ; а – константа.

Для α-частиц, испускаемых естественными α-излучателями (4 < Eα < 9 МэВ), а = 0,318, n = 1. Для α-частиц с более высокими энергиями (Eα < 200 МэВ) а = 0,148, n = 1. Так, α-частицы с энергией Eα = 5 МэВ пробегают в воздухе расстояние 3,1 см, а с энергией Еα = 30 МэВ – 68 см.

46

Отношение линейных пробегов двух видов частиц, начинающих движение в воздухе с одинаковыми скоростями, пропорционально отношению удельных потерь энергии частиц:

где m1 и m2 – массы частиц; q1 и q2 – заряды частиц.

1.15. Взаимодействие бета-частиц с веществом

Потери энергии движущимися электронами в веществе подразделяют на ионизационные и радиационные. Энергетическая зависимость удельных ионизационных потерь для электронов имеет такой же вид, как и для тяжелых заряженных частиц (см. рис.12).

Кривая потерь резко падает с увеличением скорости до кинетических энергий, равных удвоенной энергии покоя электрона, а затем медленно поднимается. Радиационные потери наблюдаются при ускоренном движении свободной заряженной частицы в электрическом поле ядра. Пролетая вблизи ядра, заряженная частица отклоняется от своего первоначального направления движения под действием кулоновской силы:

Эта сила связана с массой частицы m и её ускорением а вторым законом Ньютона F = та. Свободный заряд, движущийся с ускорением а, излучает электромагнитные волны, энергия которых пропорциональна квадрату ускорения: а2 = F2/m2. Так как а2 ≈ 1/m2, то радиационные потери тяжелых заряженных частиц значительно меньше радиационных потерь легких заряженных частиц (электронов и позитронов). Например, радиационные потери электронов в (тр/те)2 = 3,5 106 раз больше, чем протонов. Радиационные потери тяжелых частиц по сравнению с ионизационными потерями незначительны до весьма высоких энергий, и их обычно не учитывают. Однако при движении легких частиц радиационные потери могут быть весьма существенными, особенно в веществах с большим порядковым номером Z.

47

Радиационные потери преобразуются в излучение, называемое тормозным. Это излучение появляется как следствие торможения заряженных частиц в электрическом поле ядра. Тормозное излучение возникает также при движении электронов по круговым орбитам в ускорителях электронов – бетатроне и синхротроне. Эти излучения называют бетатронным и синхротронным.

Удельные радиационные потери Ер пропорциональны энергии

Ионизационные потери у электронов преобладают в области сравнительно небольших энергий. По мере увеличения кинетической энергии вклад ионизационных потерь в общие потери энергии уменьшается. Так как Еи ~ Z, отношение удельных радиационных и ионизационных потерь энергии k пропорционально ZEе : k = = 1,25 10-3 ZEе. Энергию электронов, при которой величины Еи и Ер равны (k = 1), называют критической. Критическая энергия для железа (Z = 26) равна 31 МэВ, а для свинца (Z = 82) – примерно 9,8 МэВ. Выше критической энергии радиационные потери преобладают над ионизационными. Так, в железе радиационные потери у электронов с энергией 100 МэВ в 3,25 раза, а в свинце в 10,2 раза больше ионизационных.

Тормозное излучение электронов с частотами в интервале рентгеновского излучения получают в специальных рентгеновских трубках с высоким вакуумом и тяжелым антикатодом. Его используют в медицине для диагностики болезней. Электроны в рентгеновских трубках ускоряются до 30–100 кэВ (1 кэВ = 103 эВ), а затем тормозятся в тяжелом антикатоде. При торможении электронов испускается рентгеновское излучение, характеризуемое сплошным спектром.

Масса электронов значительно меньше массы тяжелых частиц. Это и определяет характер их движения в веществе. При столкновении с атомными электронами и ядрами электроны сильно отклоняются от своего первоначального движения. Их движение происходит не по прямой линии, как у тяжелых заряженных частиц, а по извилистой траектории. Полный путь электронов в веществе значительно превосходит пробеги тяжелых заряженных частиц.

48

Однако практический интерес представляет эффективный пробег электронов. Он равен толщине вещества, которое поглощает электроны. Эффективный массовый пробег Rme электронов в алю-

где Rme измеряют в кг/м2; Ее – максимальная энергия β-частиц или

энергия моноэнергетических электронов, МэВ.

Формулы (1.15.2) с погрешностью примерно 10 % можно использовать для оценки величины Rme в воздухе и железе.

Быстрые позитроны, как и электроны, расходуют энергию в веществе на ионизацию и тормозное излучение. Замедленные позитроны, движущиеся в веществе с малой скоростью, вырывают из атома внешние электроны, которые слабее связаны с ядром, чем внутренние. Пара позитрон–электрон образует самый легкий водородоподобный атом – позитроний. В этом атоме электрон и позитрон движутся вокруг общего центра тяжести. Время жизни позитрония исчисляется миллиардными долями секунды, после чего позитрон и электрон аннигилируют (исчезают) и вместо них образуются два или три γ-кванта. Суммарная энергия γ-квантов 1,02 МэВ равна удвоенной энергии покоя электрона. Аннигиляция электрона и позитрона может происходить и без образования позитрония.

1.16.Взаимодействие электромагнитного излучения

свеществом

Рентгеновское, бетатронное, синхротронное и γ-излучения относятся к электромагнитному излучению, свойства которого зависят от частоты. Они не различаются, если их частоты совпадают. Можно рассмотреть особенности взаимодействия γ-излучения с веществом. Такие же особенности свойственны и другим излучениям в соответствующем частотном интервале γ-излучения.

γ-Излучение относится к сильнопроникающему в веществе излучению. Проходя сквозь вещество, γ-кванты взаимодействуют с

49

атомами, электронами и ядрами, в результате чего их интенсивность уменьшается. Первичными частицами называют такие частицы, которые не испытали взаимодействия с электронами, ядрами и атомами при движении в веществе.

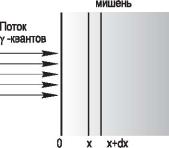
Пусть на поверхность плоской мишени перпендикулярно к ней падает поток γ-квантов (рис. 1.13). Первичный пучок в веществе ослабляется за

счет поглощения и рассеяния γ-квантов. Рассеиваясь на электроне, γ-квант теряет часть своей энергии и меняет направление своего движения. На расстоянии х от внешней поверхности плотность потока первичных γ-квантов ослабляется до величины Ф(х). В тонком слое мишени толщиной dx плотность потока уменьшается на dФ γ- квантов. Величина dФ пропорциональна величине Ф(х) на поверх-

Коэффициент пропорциональности ц называют полным линейным коэффициентом ослабления. Он имеет размерность м-1 и численно равен доле моноэнергетических γ-квантов, выбывающих из параллельного пучка на единице пути излучения в веществе. Величина μ зависит от плотности и порядкового номера вещества, а также от энергии γ-квантов:

Обозначив Ф0 плотность потока γ-квантов на поверхности мишени, можно записать закон ослабления параллельного моноэнергетического пучка первичных γ-квантов в веществе:

Ф(х) = Ф0е-μх. (1.16.3)

Величина μ равна обратной толщине вещества 1/d, где d – толщина вещества, ослабляющая плотность потока γ-квантов в е = 2,72 раза. Более удобной величиной для практического применения является слой половинного ослабления d1/2. Он равен слою вещества, ослабляющему плотность потока Ф в два раза. Величины μ и d1/2 связаны так же, как период полураспада с постоянной распада:

50