
Физика_лек_pdf / Модуль 3. Молекулярная физика. Кинематика и динамика жидкостей и газов
.pdf
Следует обратить внимание на то, что вязкость жидкостей с увеличением температуры резко снижается, а вязкость газов — возрастает.
Диффузия
Явление диффузии имеет место при контакте двух и более любых веществ — газов, жидкостей и твердых тел. Однако в газах диффузия протекает с наибольшей скоростью вследствие большей подвижности молекул газа. Обусловлено явление хаотическим движением и самопроизвольным проникновением и смешиванием однородных и разнородных газов. Следовательно, диффузия представляет собой самостоятельное перемешивание молекул при их тепловом движении. В случае перемешивания молекул одного вида принято говорить о самодиффузии. Возникает и развивается диффузия при наличии градиента плотности др /дп , кг/м4 . Градиент плотности является движущей силой явления. Диффузия сводится к обмену массой между диффундирующими компонентами. Массу вещества, которая переносится при этом через поверхность s , м2 , вдоль нормали п к этой поверхности за время t , с, определяют из закона Ф. Фика:
где D — коэффициент диффузии, который численно равен массе, переносимой через 1 м2 поверхности за 1 с при qrad ρ = д ρ/дп = 1 кг/м4 , м2 /с. Знак «минус» указывает на перенос массы в направлении убывания плотности.
Диффузионные процессы играют большую роль в природе и технике. Иллюстраций, подтверждающих это утверждение, бесконечное множество. Например, диффузия кислорода из внешней среды внутрь организма при дыхании. У растений этот процесс происходит через листья. Поэтому растительность имеет поверхность соприкосновения с окружающей средой, пропорциональную необходимому количеству кислорода. Диффузия обеспечивает также поступление других веществ в растения через корневую систему. Что же касается бесполезных и вредных для растения веществ, то они не перерабатываются растением и поэтому их концентрация внутри и у поверхности корней быстро уравнивается с концентрацией этих веществ в почве. Таким образом, диффузия помогает растению произвести отбор необходимых веществ. Диффузионные процессы обеспечивают также деятельность пищеварительной системы животных и человека. Пища, как известно, в желудке и кишечнике переходит в растворенное состояние, и нужные организму вещества диффундируют через стенки пищеварительного тракта. Интересен и следующий пример из общественной жизни муравьев. Они узнают и помнят друг друга только из своего сообщества по запаху кожи, выделяющей специфический углерод. Если после трехмесячной совместной жизни насекомых разделяют на 2 группы, то этот запах сохраняется до 18 месяцев.
В технике явление диффузии положено в основу процессов экстракции — извлечения отдельных компонентов из сложных по составу систем: производство красителей, дубильных и других веществ в химическом производстве, сахара из свеклы. Диффузия как явление имеет место и в твердых телах. Коэффициент диффузии в твердых металлах в ≈ 106 раз меньше, чем в жидкостях. Тем не менее диффузия широко используется в процессах обработки металлов, так как существенно влияет на свойства металлов. При накаливании, например, железа с углем последний диффундирует в железо. Происходит науглероживание железных изделий. В обработке металлов этот процесс называют цементацией. Цементацию производят нагреванием изделий совместно с сажей, древесным углем, коксом или в газообразной среде окиси углерода при температуре от
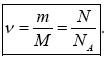
600 до 1000 °С. Цементация способствует поверхностной закалке изделий с образованием твердого наружного слоя и сохранением вязкой сердцевины.
Из теоретических рассуждений следуют зависимости между коэффициентами переноса λ, η и D : η = ρD , Па · с, и λ = ηс v Вт/(м · К), где ρ и с v — соответственно плотность и массовая изохорная теплоемкость вещества, кг/м3 и Дж/(кг · К). Коэффициенты теплопроводности, диффузии и динамической вязкости при проведении практических расчетов процессов переноса берут из справочной литературы в зависимости от температуры и давления конкретного газа.
Цит . по: Физика: учебник / Демидченко В .И . — Ростов н/Д: Феникс , 2006 . — С . 91–98 .
Основные понятия, модели, положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории:
1.Все вещества состоят из огромного количества частиц. Наименьшая частица
вещества, сохраняющая его химические свойства, называется молекулой. Размеры молекул малы 10-8 –10-9 см. Количество огромно: в 1 см3 газа при н.у. содержится приблизительно 3·1019 молекул. Явления, подтверждающие это положение — испарение, растворение, сжатие.
2.Все молекулы непрерывно и хаотично движутся. Хаотичность проявляется в том, что в газе любое направление движения молекул равновероятно. Явления, подтверждающие это положение — диффузия, броуновское движение.
3.Молекулы взаимодействуют между собой. Это происходит посредством молекулярных сил. На далеких расстояниях это силы притяжения, убывающие с увеличением расстояния; на близких — силы отталкивания, быстро возрастающие при сближении молекул. Доказательство этого положения — твердые тела сохраняют свою форму и объем.
Основные понятия молекулярно-кинетической теории:
1)Относительная атомная масса химического элемента Аr — отношение массы атома этого элемента к 1/12 массы атома изотопа углерода 12 С. Находится из таблицы химических элементов Менделеева. Например, Аr (16 О8 ) = 16. Относительная
молекулярная масса вещества Mr — отношение массы молекулы этого вещества к 1/12 массы атома изотопа углерода 12 С.
2)Моль — количество вещества, в котором содержится количество частиц равное числу атомов в 12 г изотопа углерода 12 С.
3)Постоянная Авогадро — число частиц в одном моле вещества NA = 6,02·1023
моль-1 .
4)Молярная масса — масса одного моля вещества 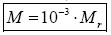 (кг/моль).
(кг/моль).
5)Число молей вещества:
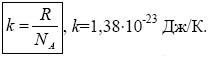
6)Газовая постоянная R = 8,31 Дж/(моль·К)
7)Постоянная Больцмана — доля газовой постоянной, приходящейся на 1 молекулу:
9)Нормальные условия (н.у.): температура 273 К = 0°С; давление: 1 атм = 10-5 Па.
10)Объем одного моля любого газа при н.у. по закону Авогадро равен 22,4 л.
11)Идеальный газ — газ, взаимодействием между молекулами которого можно пренебречь.
Цит . по: Конспект лекций по дисциплине «Физика» для студентов технических специальностей заочной формы обучения . Ч . 1 / Сост . В .А . Сарафанова / — Тольятти: ТГУ , 2008 . — С . 32–33 .
Тема 3. Явления переноса в газах
Средняя длина свободного пробега
1. Средняя скорость теплового движения газовых молекул определяется формулой (73.6). Уже при комнатной температуре она порядка скорости ружейной пули. Например,
при 0 °С для молекул водорода, азота и кислорода  равна соответственно 1700 м/с, 455 м/с и 425 м/с. На ранней стадии развития кинетической теории газов столь большие значения скоростей молекул некоторым физикам казались невозможными. Если скорости молекул действительно так велики — говорили они, — то запах пахучего вещества должен был бы распространяться от одного конца комнаты к другому практически мгновенно. На самом деле при отсутствии конвективных потоков воздуха время распространения запаха на такие расстояния может составлять многие минуты и даже часы. Распространение запаха осуществляется посредством медленного процесса диффузии .
равна соответственно 1700 м/с, 455 м/с и 425 м/с. На ранней стадии развития кинетической теории газов столь большие значения скоростей молекул некоторым физикам казались невозможными. Если скорости молекул действительно так велики — говорили они, — то запах пахучего вещества должен был бы распространяться от одного конца комнаты к другому практически мгновенно. На самом деле при отсутствии конвективных потоков воздуха время распространения запаха на такие расстояния может составлять многие минуты и даже часы. Распространение запаха осуществляется посредством медленного процесса диффузии .
Для демонстрации медленности диффузии газов можно взять стеклянный цилиндр высоты примерно 30 см, закрытый сверху проволочной сеткой. Вдоль оси цилиндра пропущена тонкая стеклянная палочка или трубка, к которой на равных расстояниях прикреплено около 10 полосок фильтровальной бумаги, смоченных в фенолфталеине. На сетку сверху кладется вата, смоченная нашатырным спиртом. Выделяющийся аммиак диффундирует вниз. Диффузия наблюдается по покраснению полосок фильтрованной бумаги. Через 1–2 минуты начинается покраснение верхней полоски. Нижняя полоска начинает краснеть минут через 20. Аммиак легче воздуха, поэтому его проникновение вниз происходит только в результате диффузии. Стеклянный цилиндр служит для предотвращения возникновения потоков воздуха.
Значительно медленнее происходит диффузия в жидкостях, хотя скорости теплового движения здесь такие же, что и в газах и в твердых телах. Если узкий и высокий стеклянный цилиндр наполнить дистиллированной водой, а затем на дно с помощью специальной трубки осторожно опустить кристаллы медного купороса, то последние растворяться, и начнется диффузия. Чтобы ее заметить на глаз, нужны сутки или
несколько суток. А для того чтобы получился однородный раствор по всей высоте цилиндра, требуется несколько месяцев. В твердых телах диффузия происходит еще медленнее, и требуются специальные методы, чтобы ее обнаружить.
Так же медленно происходит выравнивание температур между различными частями неравномерно нагретого газа посредством теплопроводности или выравнивание скоростей макроскопического движения газа посредством сил вязкости.
2. Медленность диффузии и аналогичных ей явлений Клаузиус объяснил столкновениями молекул . Молекула газа не все время движется свободно, а время от времени испытывает столкновения с другими молекулами. Свободно она пролетает короткое расстояние от одного столкновения до следующего. В момент столкновения скорость молекулы испытывает резкое изменение как по модулю, так и по направлению. В результате траектория молекулы получается не прямой, а ломаной линией с большим количеством звеньев. Молекула беспорядочно мечется туда и сюда, и ее общее продвижение вперед происходит сравнительно медленно. Для количественного описания явления Клаузиус ввел понятие средней длины свободного пробега , т.е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего.
Для вычисления средней длины свободного пробега будем пользоваться моделью твердых шаров . Между столкновениями молекулы шары движутся по инерции прямолинейно и равномерно. В моменты столкновений между молекулами развиваются очень большие силы отталкивания, изменяющие их скорости по величине и направлению. Разумеется, такая грубая модель передает далеко не все черты явлений, которые происходят при столкновениях. Молекулы могут распадаться и соединяться. Атомы могут ионизоваться, переходить в возбужденные состояния и т.д. Все это оставим сейчас без внимания. Модель твердых шаров может приблизительно правильно описать только процессы рассеяния , молекул, в которых происходят изменения скорости и направления движения этих частиц в результате столкновений их между собой и со стенками сосуда, в котором заключен газ.
Для упрощения расчета предположим, что движется только одна молекула с постоянной скоростью v , а все остальные молекулы неподвижны. Будем называть движущуюся молекулу молекулой А . Вообразим, что с молекулой А жестко связана концентрическая с ней твердая сфера S вдвое большего диаметра. Назовем эту сферу сферой ограждения , молекулы А . В момент столкновения расстояние между центрами сталкивающихся молекул равно диаметру молекулы d . Следовательно, в этот момент центр неподвижной молекулы, с которой столкнулась молекула А , окажется на поверхности сферы ограждения последней. Очевидно, он не может проникнуть внутрь этой сферы. Между двумя последовательными столкновениями молекулы А ее сфера ограждения описывает цилиндр, длина которого и есть свободный пробег молекулы А . Из таких цилиндров складывается поверхность, описываемая с течением времени сферой ограждения (рис. 75). Для краткости будем называть эту поверхность ломаным цилиндром. Если центр другой молекулы лежит внутри или на боковой поверхности этого цилиндра, то она столкнется с молекулой А . В противном случае столкновения не произойдет. Пусть V — объем ломаного цилиндра, описываемого сферой S в единицу времени. Среднее число z столкновений движущейся молекулы с остальными молекулами в единицу времени равно среднему числу последних в объеме V , т. е. z = Vn , где п — число молекул в единице объема. Мы предполагаем, что средняя длина свободного пробега λ очень велика по сравнению с диаметром сферы ограждения 2 d . Тогда можно пренебречь теми частями объема V , которые приходятся на изломы цилиндра, т. е. при вычислении V цилиндр можно считать прямым, а его высоту равной скорости молекулы v

. В этом приближении V = ζ v , где ζ = π d 2 — площадь поперечного сечения цилиндра. Следовательно,
z = n ζ v . (86.1)
Рис . 75
Путь, пройденный молекулой А за единицу времени, равен v . Разделив его на среднее число столкновений z , найдем среднюю длину свободного пробега молекулы:
λ = 1 /п ζ. (86.2)
Из вывода следует, что при получении формул (86.1) и (86.2) можно рассуждать так, как если бы все молекулы, с которыми сталкивается молекула А , были точечными, а радиус молекулы А увеличен вдвое, т.е. молекула А заменена ее сферой ограждения. Такая замена может рассматриваться как вычисленный прием для учета конечных размеров молекул, сталкивающихся с молекулой А . Этот прием будет использован в следующем параграфе при введении понятия эффективного сечения.
Конечно, формулы (86.1) и (86.2) не точны, поскольку в основу их вывода, положено предположение, что движется только одна молекула, а все остальные неподвижны. Математически строгий расчет был дан Максвеллом с учетом максвелловского распределения молекул по скоростям. Но в физике уточнение Максвелла мало существенно, так как его расчет выполнен не для реальных молекул, а для модели твердых упругих шаров. Максвелл получил:
Выражения (86.3) и (86.4) отличаются от приближенных формул (86.1) и (86.2) только числовыми коэффициентами, близкими к единице. Это несущественно во всех расчетах, которые сами проводятся с точностью до числовых коэффициентов. Такое положение имеет место в излагаемой ниже теории явлений переноса — диффузии , внутреннего трения и теплопроводности . Ввиду сложности точной теории этих явлений приходится довольствоваться приближенными расчетами, часто довольно грубыми. В
таких расчетах несущественно сохранять числовые множители  и
и  , что обычно и делается. Упрощенные формулы (86.1) и (86.2) дают не только правильные порядки величин, но, что особенно важно, приводят к верной зависимости числа столкновений и длины свободного пробега от концентрации и размеров молекул.
, что обычно и делается. Упрощенные формулы (86.1) и (86.2) дают не только правильные порядки величин, но, что особенно важно, приводят к верной зависимости числа столкновений и длины свободного пробега от концентрации и размеров молекул.

3. Сам Максвелл получил выражения (86.3) и (86.4) в результате довольно кропотливых и сложных вычислений. Между тем их можно получить из формул (86.1) и (86.2) путем весьма простых рассуждений почти без вычислений. Появление множителя
 становится при этом особенно ясным. Приведем соответствующий вывод.
становится при этом особенно ясным. Приведем соответствующий вывод.
При рассмотрении процесса столкновения играет роль не абсолютная скорость выделенной молекулы А , а ее скорость относительно молекулы , с которой она ,
сталкивается . Выделим мысленно группу молекул, которые движутся относительно молекулы А с одной и той же относительной скоростью v i отн. Пусть ni — число таких молекул в единице объема. Число столкновений zi молекулы А с молекулами выделенной группы в единицу времени можно найти по формуле (86.1), которая даст zi = ni , ζ v i отн. . Полное число столкновений молекулы А со всеми остальными молекулами найдется суммированием этого выражения по всем скоростным группам, т. е. по всем возможным значениям индекса i :
Введя среднюю относительную скорость
получим
 (86.5)
(86.5)
и, следовательно,
(86.6) |
|
Задача свелась к вычислению средней относительной скорости |
какой-либо молекулы |
относительно всех остальных молекул газа. |
|
4. Для решения этой задачи дадим другую интерпретацию максвелловского закона распределения скоростей. В прежней интерпретации закон Максвелла , давал распределение скоростей всех молекул газа , в один и тот , же момент , времени . Но па него можно смотреть как па закон распре деления скоростей одной и той же молекулы
(например, молекулы А ), которые она последовательно принимает в различные моменты времени. Воспользуемся следующей интерпретацией. Пусть v 1 , v 2 ,..., v N — скорости, принимаемые молекулой А непосредственно после первого, второго и последующих столкновений. Если число N стремится к бесконечности, то эти скорости распределятся по закону Максвелла. Это непосредственно следует из равноправия всех молекул и хаотичности молекулярного теплового движения. В моменты столкновений на молекулу А действуют беспорядочно меняющиеся силы F 1 , F 2 , … Они-то и приводят к установлению максвелловского распределения скоростей молекул А в рассматриваемые моменты времени. Под v 1 , v 2 ,..., v N мы понимаем скорости относительно системы отсчета, в которой газ как целое покоится. Введем теперь скорости молекулы А

относительно остальных молекул, которыми она обладала в промежутках между последовательными столкновениями. Пусть v означает скорость молекулы А после первого столкновения относительно молекулы , с которой произошло это столкновение , v — скорость после второго столкновения относительно молекулы , с которой произошло это второе столкновение , и т.д. Как известно из механики, при рассмотрении относительного движения двух частиц одну из них можно считать неподвижной. Относительное движение второй частицы (например, частицы А ) формально описывается уравнением Ньютона, как в неподвижной системе. При этом силы F 1 , F 2 , … остаются прежними, но масса частицы А должна быть заменена приведенной массой. Если молекулы одинаковы ( m 1 = m 2 = т ), то приведенная масса равна m 1 m 2 /( m 1 + m 2 ) = т /2. Таким образом, при относительном движении все происходит так, как если бы масса молекулы уменьшилась в два раза. Так как силы F 1 , F 2 , … и моменты времени их действия остались прежними, то в эти моменты относительные ускорения молекулы А будут вдвое превосходить ее же ускорение в неподвижной системе отсчета. Отсюда непосредственно следует, что распределение относительных скоростей молекулы будет максвелловским . А так как эффективная масса молекулы в относительном движении вдвое меньше т , то все средние относительные скорости окажутся больше
соответствующих абсолютных скоростей в |
раз. |
В частности, |
, и |
формулы (86.5) и (86.6) переходят в (86.3) и (86.4). |
|
|
|
5. Рассмотрим теперь более важный случай, когда сталкивающиеся молекулы |
|||
различны. Пусть одна молекула сорта 1 с массой m 1 |
и радиусом r 1 |
движется в среде |
|
молекул сорта 2 с массами т 2 , радиусами r 2 |
и концентрацией п 2 . Если бы молекулы |
||
сорта 2 были неподвижны, то остались бы справедливыми прежние формулы (86.1) и
(86.2). В них надо было бы только заменить z на 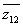 , п — на n 2 , v — на
, п — на n 2 , v — на  , ζ на ζ12 = π( r 1 + r 2 )2 . Сферой ограждения молекулы 1 теперь является концентрическая с ней сфера
, ζ на ζ12 = π( r 1 + r 2 )2 . Сферой ограждения молекулы 1 теперь является концентрическая с ней сфера
радиуса d = r 1 + r 2 . Учтем теперь максвелловское распределение скоростей, используя формулы (86.5) и (86.6). На основании изложенного выше средняя относительная
скорость  и средняя скорость молекулы
и средняя скорость молекулы  обратно пропорциональны квадратным корням
обратно пропорциональны квадратным корням  и
и  , т. е.
, т. е.
С учетом соотношения  этот результат можно представить в более симметричной форме:
этот результат можно представить в более симметричной форме:
(86.7)
Для среднего числа столкновений  , претерпеваемых молекулой сорта 1 с молекулами сорта 2 в единицу времени, получаем
, претерпеваемых молекулой сорта 1 с молекулами сорта 2 в единицу времени, получаем
 (86.8)
(86.8)

а для средней длины свободного пробега молекулы сорта 1
(86.9)
При m 1 = m 2 эти выражения переходят в максвслловские формулы (86.3) и (86.4).
6. Наконец, рассмотрим случай смеси двух различных газов. Пусть r 1 и r 2 означают радиусы молекул этих газов, а n 1 и n 2 — их концентрации. Теперь движущаяся молекула может сталкиваться не только с молекулами, себе подобными, но и с молекулами другого типа. В соответствии с этим с ней следует связать две сферы ограждения в зависимости от того, с молекулами какого типа она сталкивается. Введем четыре величины
Для чисел столкновений в единицу времени молекулы первого и молекулы второго газов получаем соответственно (без учета максвелловского распределения скоростей)
(86.10)
а для средних длин свободного пробега.
(86.11)
Эффективное сечение
1. Площадь сечения сферы ограждения молекулы по большому кругу называется эффективным сечением молекулы , точнее , газокинетическим эффективным сечением молекулы при рассеянии ее на других молекулах . Если рассеяние происходит на таких же молекулах, то эффективное сечение ζ = π d 2 , где d — диаметр молекулы. Если же
молекула радиуса r 1 рассеивается на молекулах с радиусом r 2 , то эффективное сечение будет ζ = ζ 12 = π( r 1 + r 2 )2 .
Понятие эффективного сечения широко используется при рассмотрении различных явлений, возникающих при столкновении частиц. При столкновении частица, может изменить направление своего движения, т. е. рассеяться. Она может поглотиться, диссоциировать молекулу или ионизовать атом, с которыми она сталкивается, и т. д. В
соответствии с этим говорят об эффективных сечениях рассеяния , поглощения ,
диссоциации , ионизации и пр. Во всех таких случаях при вычислении среднего числа столкновений, приводящих к требуемому результату, можно для наглядности представить, что рассматриваемая частица (будем продолжать называть ее частицей А ) окружена, некоторой непроницаемой «сферой ограждения», а частицы, с которыми она сталкивается, являются точечными. Если частица. A движется, а прочие частицы неподвижны, то они называются полевыми частицами , а частица А — пробной частицей . Среднее число столкновений пробной частицы с полевыми определяется формулой (86.1), где п — концентрация полевых частиц, а v — скорость пробной частицы относительно полевых. На формулу (86.1) следует смотреть как на определение понятия эффективного сечения ζ соответствующего процесса.
В экспериментах по столкновениям ядерных и элементарных частиц более удобна, другая интерпретация формулы (86.1) и эффективного сечения. Здесь обычно бывает неподвижна частица А , а прочие частицы налетают и бомбардируют ее. В связи с этим эти частицы, если они движутся параллельно, называются пучком , а частица. А — мишенью , которую они бомбардируют. Величина I = n v есть интенсивность пучка , т.е. число частиц, проходящих через единичную площадку, перпендикулярную к пучку, в единицу времени. Применительно к рассматриваемому случаю формулу (86.1) следует переписать в виде
 (87.1)
(87.1)
Величина N = z означает среднее число частиц, выбывших из пучка в единицу времени в результате столкновений с частицей-мишенью А . Таким образом, можно дать следующее определение эффективного сечения частицы по отношению к какому-либо процессу. Эффективным сечением ζ называется отношение среднего числа частиц , выбывших из пучка в единицу времени при столкновениях , приводящих к требуемому результату (рассеянию пучка, поглощению, ионизации, прилипанию и пр.), к интенсивности самого пучка . Преимущество такой интерпретации эффективного сечения состоит в том, что она не связана ни с какими модельными представлениями.
2.Эффективное сечение тех или иных процессов, вообще говоря, сильно зависит от относительной скорости сталкивающихся частиц. Рассмотрим, например, ионизацию
атомов при столкновениях. Если кинетическая энергия εотн относительного движения сталкивающихся атомов меньше энергии ионизации атома, то последняя невозможна.
Эффективное сечение ионизации равно в этом случае нулю. Когда εотн равна энергии ионизации или превосходит ее, ионизация становится невозможной. Ясно поэтому, что
эффективное сечение ионизации должно зависеть от относительной скорости v отн сталкивающихся атомов. Сильная зависимость эффективного сечение от v отн имеет место для таких процессов, как поглощение нейтронов атомными ядрами, деление тяжелых атомных ядер под действием нейтронов, химические и термоядерные реакции и пр. Расчет эффективных сечений подобных процессов производится с помощью законов и вычислительных методов квантовой механики. В настоящей теме речь будет идти только
опроцессах упругого рассеяния молекул и атомов на других молекулах и атомах. В этих случаях внутреннее состояние сталкивающихся частиц не изменяется. Эффективное же сечение таких процессов очень слабо зависит от относительной скорости частиц. Вот почему для их изучения можно пользоваться моделью твердых шариков, в которой поперечное сечение ζ совсем не зависит от относительной скорости.
3.В действительности наблюдается некоторое уменьшение эффективно го сечения рассеяния молекул с увеличением относительной скорости. Объяснение этому было дано Сѐзерлендом (1859–1912) в 1893 г. Он использовал модель твердых упругих шаров, но учел силы притяжения, с которыми молекулы действуют друг на друга в промежутках между столкновениями. Силы притяжения несколько сближают молекулы, пролетающие мимо друг друга, и делают возможными некоторые столкновения, которые при отсутствии этих сил не могли бы произойти. Это ведет к увеличению эффективного сечения рассеяния ζ.
Исследуем вопрос с количественной стороны. Рассматривая относительное движение, молекулу А будем считать неподвижной, а молекулу В — движущейся (рис. 77). Относительную скорость молекулы В на бесконечности обозначим через v 0 . Пусть b
прицельное расстояние между молекулами , т. е. длина перпендикуляра, опущенного из

центра молекулы А на направление прямой, вдоль которой направлен вектор v 0 . Если молекулы не взаимодействуют и b > d , то столкновение между ними невозможно. При наличии же сил притяжения столкновение может произойти и в этом случае, как это видно из рис. 77 б . Если b максимальное значение прицельного расстояния, при котором столкновение еще произойдет, то эффективное сечение будет ζ = π b 2 . Эффективное сечение при отсутствии сил притяжения ζ0 = π d 2 . Так как силы — центральные, то по закону площадей v 0 b = v d , где v — скорость молекулы В в момент максимального сближения с А . Возведя в квадрат, получим ζ v 0 2 = ζ 0 v 2 . Скорость v найдется из уравнения энергии (1/2)μ v 2 = (1/2)/μ v 0 2 + А , где А — работа центральных сил притяжения при перемещении молекулы В из «бесконечности» в положение максимального сближения с молекулой A , a μ приведенная масса. Введем кинетическую энергию относительного движения εотн = (1/2)/ μ v 0 2 . Тогда
или
Рис . 77
Эта формула, как ясно из ее вывода, применима в тех случаях, когда имеется всего одна пара взаимодействующих молекул А и В . Применять ее к молекулам газа можно только при условии, когда взаимодействия в газе могут рассматриваться как парные . В этом приближении учитываются силы притяжения, действующие на молекулу только со стороны одной молекулы, достаточно сблизившейся с рассматриваемой. Действия всех остальных молекул не учитываются. Так можно поступать, когда газ достаточно разряжен, а молекулярные силы притяжения убывают с увеличением расстояния между взаимодействующими молекулами достаточно быстро. Случаи, когда в разряженном газе сближаются и начинают взаимодействовать три и больше молекулы, маловероятны и по этой причине не принимаются во внимание.
В случае газа εотн может принимать всевозможные значения при переходе от одной пары взаимодействующих молекул к другим. Поэтому целесообразно ввести некоторое
среднее эффективное сечение молекулы , усреднив 1/εотн по всем относительным скоростям. Выполнив это и обозначая усредненное эффективное сечение прежней буквой ζ, очевидно, придем к формуле вида
 (87.2)
(87.2)
