Абрамов А.И., Пустынский Л.Н., Романцов В.П. Лабораторный практикум по курсу Ядерная и нейтронная физика

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ОБНИНСКИЙ ИНСТИТУТ АТОМНОЙ ЭНЕРГЕТИКИ

Физико-энергетический факультет

А.И.Абрамов, Л.Н.Пустынский, В.П.Романцов

Лабораторный практикум по курсу

"Ядерная и нейтронная физика" Часть 1

ОБНИНСК 1997

Абрамов А.И., Пустынский Л.Н., Романцов В.П. Лабораторный! практикум по курсу "Ядерная и нейтронная физика". Часть 1. -Обнинск: | ОИАТЭ,1997,-132с.

]

Предлагаемое пособие является первой частью лабораторного! практикума по курсу "Ядерная и нейтронная физика" для i специальностей 013100 (ЭКЛ), 070500 (Р), 070500Ф(Ф), 330300 (РБ), 101000 <ФХП), 101002 (Э), 101000 (МН). Авторы решили включить в пособие теоретические вопросы в объеме, необходимом для подготовки и сдачи лабораторных работ без обращения к другим источникам.' Практические руководства для работы с конкретными приборами находятся на столах в лаборатории и называются "Инструкции".

А.И.Абрамов написал работу №6 и дополнительное задание к работе №7. Л.Н.Пустынским написаны работы №2, №3, №4 (совместно

сВ.П.Романцовым), №5, №7. Работа № 1 написана В.П.Романцовым.

Впостановке лабораторных работ в различные годы принимали участие Ю.И.Каширцев, А.В.Лебедев и И.М.Новиков. Авторы выражают свою признательность и благодарность И.В.Романцовой за большой труд по подготовке данного издания к выходу в свет.

Илл. 42, табл. 13, библ. назв. 9

Темплан 1997, поз. 36

Работа 1. Изучение статистических распределений

Цель работы. Экспериментальное изучение биномиального и пуассоновского распределений и аппроксимации пуассоновского распределения нормальным. Построение приближений к генеральным распределениям по оценкам средних из больших выборок и сравнение с непосредственно выборочными распределениями. Анализ расхождений.

Введение

Результат любого физического измерения по своей сути случаен и никогда не отображает действительную картину физического явления или процесса. Если объект измерений макроскопический, т.е. представляет собой ансамбль из очень большого числа частиц, отклонение результата измерений от действительного значения измеряемой величины будет обусловлено точностью прибора, влиянием неконтролируемых воздействий на элементы прибора, методикой и моделью измерений. Неопределенность самой физической величины, связанная с ограниченностью ансамбля, при макроскопических измерениях пренебрежимо мала. Если же объект измерений микроскопический • молекулы, атомы, ядра, элементарные частицы, - то отклонение результата отдельного измерения от результатов любых повторных измерений обусловлено характером самого физического явления. Действительное значение здесь может пониматься только в статистическом смысле как результат некоторого усреднения по большому количеству одинаковых повторений конкретного явления. Изучение относительных разбросов результатов, т.е. статистический анализ, является основным инструментом исследования микроскопических процессов; с помощью статистического анализа из экспериментальных результатов извлекается информация о природе физических явлений.

Для макроскопических измерений отклонение результата от действительного значения можно назвать "погрешностью" или "ошибкой" измерения, но для микроскопических - эти термины уже употреблять нельзя. Здесь лучше пользоваться терминами "разброс", "флуктуация", "отклонение". Само же физическое явление должно рассматриваться как случайное событие.

3

1. Случайные события, случайные величины и способы их описания

Случайным событием будем называть событие, факт наблюдения которого зависит от случайных причин. Важнейшая характеристика случайного события - вероятность его появления. Под вероятностью будем понимать среднюю частоту появления данного события при многократной (в пределе бесконечной) реализации условий его наблюдения. Это положительное число, не превосходящее единицу; достоверное событие имеет вероятность, равную единице, а невозможное - нулю. Вероятность события А будем обозначать p A .

Если факт появления одного события не влияет на возможность появления другого, то такие события называются независимыми. Например, радиоактивный распад одного ядра в источнике не влияет на возможность распада других, генетически не связанных с ним ядер. В противном случае, когда появление одного случайного события оказывает влияние на появление другого, то события будут зависимыми. Например, при распаде ядра продукт распада может оказаться в возбужденном состоянии, возбуждение снимается испусканием гамма-квантов или каких-либо частиц; таким образом, от события-распада зависит возможность появления других событий - испускания гамма-квантов или частиц.

Понятие случайного события широко используется при исследовании случайных величин. Например, случайным событием может быть факт непревышения некоторым измеренным значением (случайной величиной) заданного порогового значения или факт нахождения измеренного значения в заданном интервале, или факт описания физического явления некоторой математической формулой (моделью) и т.п.

Случайной величиной будем называть величину, наблюденное значение которой зависит от случайных причин. Полный набор из всех возможных значений, которые может принимать случайная величина

X, будем называть генеральной совокупностью Q ,при этом p x Q 1, т.е. принадлежность x генеральной совокупности есть

достоверное событие. Генеральная совокупность может быть и набором (конечным или бесконечным) дискретных значений, и непрерывным

4

континуумом (ограниченным или неограниченным). Случайная величина характеризуется полностью, когда известны все вероятности принимать те или иные значения из генеральной совокупности. Если эти вероятности можно представить в виде математических функций, где аргументом является значение случайной величины, то такие функ-

ции называют функциями распределения случайной величины. Когда в качестве случайной величины выбран результат измерения, то обычно используется функция плотности распределения вероятностей появления тех или иных значений случайной величины. У дискретной случайной

величины каждому ее значению из генеральной совокупности xi . приписывается вероятность появления этого значения p(xi ) . Если случайная величина непрерывна, то ее функцией плотности распределения вероятностей f(x) будет вероятность появления величины x в

интервале dx, отнесенная к этому интервалу dx при dx —>0. Очевидно,

Строго говоря, функция распределения плотности вероятностей может применяться лишь как характеристика непрерывной случайной величины. Однако, используя понятие дельта-функции Дирака*, можно записать функцию плотности распределения дискретной случайной величины и ее интеграл по генеральной совокупности:

f (x) p(xi ) (x xi );

Здесь не должен вызывать удивления факт, что f(x) становится

---------------------------------------------------------------------------------

* Дельта-функция (x t) 0 всюду, кроме x t , где функция ста-

новится бесконечной и притом такой, что (x t)dt 1

Из специальных свойств дельта-функции нам необходимо

одно: f (t) (x t)dt f (x)

5

xi

совокупности - конечная величина.

Плотность распределения вероятностей f(x) полностью описывает все свойства случайной величины х. Однако при физических измерениях точное знание f(x) требуется далеко не всегда, часто достаточно знать некоторые характеристики f(x), чтобы составить представление об измеряемой величине и о возможной ее флуктуации при измерении. К таким характеристикам относятся математическое ожидание x случайной величины х и ее дисперсия Dx.

Математическим ожиданием x случайной величины называют

ее среднее значение, для непрерывной случайной величины вычисляемое как интеграл по генеральной совокупности:

а для дискретной - как сумма по всем значениям из генеральной совокупности

Дисперсия случайной величины характеризует меру ее разброса вокруг математического ожидания и представляет собой математическое ожидание квадрата отклонения случайной величины от ее среднего.

Для непрерывных случайных величин

При макроскопических измерениях, когда f(x) 'характеризует распределение приборных и методических погрешностей, значение x характеризует само измеряемое значение, a Dx - возможную случайную

6

ошибку измерений. Для микроскопических величин x и Dx являются

характеристиками распределений самих измеряемых величин и помогают'понять сущность физического явления, но не описывают это явление полностью.

Раскрывая в (1.4а) и (1.4) скобки под интегралом и суммой, можно получить формулы, зачастую более удобные при вычислениях дисперсии:

т.е. дисперсия есть разность между средним квадратом случайной величины и квадратом ее среднего.

Положительное значение корня квадратного из дисперсии имеет размерность самой физической случайной величины и называется сред-

неквадратичный или стандартным отклонением для распределения случайной величины (среднеквадратичной погрешностью можно на звать только в случае макроскопических измерений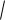!), x Dx

причем для обозначения дисперсии вместо Dx иногда используют x2 Если неизвестно, какова функция плотности распределения f(x) случайной величины, но известны ее математическое ожидание x и

дисперсия x2 или их хорошие оценки (понятие "хорошие" обусловлено приводимыми ниже неравенствами), то для вероятностных оценок разброса экспериментальных значений, независимо от вида f(x), полезно воспользоваться неравенством Чебышева

купности удалено от математического ожидания больше, чем на n x никогда не превысит величины1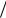n2 где п > 1 - наперед

заданное число. Если же нам известно, что f(x) имеет один максимум (одномодальна) и симметрична относительно x , но сам вид функции

7

f(x) по-прежнему неизвестен, неравенство Чебышева может быть усилено более, чем вдвое:

Большинство физических экспериментов базируется на измерении одной или нескольких случайных величин, а конечным результатом является некоторая функция, составленная из этих случайных величин. Чтобы оценить математическое ожидание и разброс конечного результата, полезно знать следующие теоремы.

1.Для постоянной величины матожидание равно самой величине, а дисперсия равна нулю.

2.Среднее значение отклонений случайной величины от ее математического ожидания равно нулю:

3. Постоянный множитель можно выносить как коэффициент перед математическим ожиданием линейной функции от случайной величины вида ах:

С

4.Постоянный множитель можно выносить за знак дисперсии при ее вычислении для функции вида ах, возведя его в квадрат:

5. Среднее значение линейной комбинации нескольких случайных величин, зависимых или независимых*, равно сумме средних значений всех слагаемых, т.е. если

'Случайные величины x1 , х2,... ,хк называются независимыми в совокупности или просто независимыми, если функция распределения случайного вектора х —( x1 ,x2,..., хк) представима в виде произве-

дения f (x1 ) f (x2 ) .... f (xk ) .

8

6. Среднее значение произведения независимых (и только!) случайных величин равно произведению их математических ожиданий, т.е. если

9. Дисперсию функции y (x) от случайной величины х можно оценить по формуле

dy 2

Dy Dx (1.15)

dx

где значение производной вычисляется в какой-либо точке вблизи математического ожидания x .

10. Дисперсию функции y (x1 , x2 ,....., xk ) от нескольких независимых (!) случайных величин можно оценить по формуле