6. 7.2.2.7. Целевые функции с учетом граничных условий повреждения

Здесь применим критерий . Рассмотрим запись этого критерия для различных замыканий.

1. Однофазное замыканиеРассмотрим прямой критерий. Воспользовавшись целевой функцией (1*) получим

Корень этого уравнения не изменится, если заменить в нем ток любым другим комплексом с той же фазой. Тогда с учетом граничных условий дляпрямой целевой функции будут сопутствовать косвенные, представляющие собой взаимные реактивные мощности: напряжения в месте предполагаемого повреждения и некоторых токов

Рассмотрим свойства целевых функций на модели.

Передающая система представлена ЭДС и эквивалентным сопротивлениемПредшествующему режиму (рис.а) соответствует верхний годограф на векторной диаграмме (рис.г). Источником коммутационных токов служит предшествующее напряжение(рис. б). Реакция на него – ток повреждения: он сам, его слагаемыеи, а, следовательно, и токи линии, со слагаемымиотстают от векторана угол, не превышающий. В режиме КЗ (рис.в) расчетный годограф напряжений смещается относительно предшествующего положения на величины падений напряжений в схеме по рис.б, причем новый годограф и векторпересекутся в единственной точке. Векторыисовпадут, расчетные же векторы точекопережают токтак что

и целевая функция , а для точекотстают от него, так что

Рис. а. Предшествующий докоммутационный режим

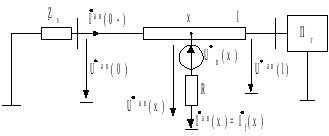
Рис. б. Коммутационный режим

Рис. в. Послекоммутационный режим

2. Двухфазное замыканиеПрямой целевой функции

отвечают косвенные

3. Двухфазное замыкание на землю Прямая целевая функция в данном случае имеет вид

(К4*)

а косвенная, в предположении

Здесь возможны и другие варианты.

и вместо (К4*) можно ввести упрощенную (пока еще прямую) функцию

а затем уже – косвенную функцию

Возможен и иной подход:

приводящий сначала к прямой целевой функции

а затем в соответствии

к косвенной

4. Трехфазное замыкание Прямой целевой функции будет соответствовать косвенная

7. 7.2.2.8. Дистанционные способы на основе косвенных критериев

Вне зависимости от вида КЗ повреждение на ЛЭП идентифицируется по условию

Формула

выведена для ЛЭП с односторонним питанием. По аналогии выражение для ЛЭП межсистемной связи запишется

которое дает наглядное представление о поведении функции вдоль линии.

Метод дистанционных критериев позволяет сформулировать подход к алгоритму ДЗ. Если КЗ в зоне, когда зависимостьпо концам зоны имеет разные знаки

Если же КЗ вне зоны, когда , то

и, наконец, при замыкании «за спиной», когда ток

предполагаемого повреждения в любой точке реально неповрежденной линии, определяемый

будет иметь нулевой уровень. Последнее и служит свидетельством того, что участки ЛЭП правее места установки защиты не повреждены.

В соответствии с выражением

при подлежат определению знаки

Входящие в эти выражения величины иизмеряются непосредственно, либо поступают (вычисляются) с выходов соответствующих фильтров. Что же касается величины , то она измерению недоступна и определяется в предположении, что линия не повреждена во всей контролируемой зоне, или, иначе говоря, повреждение может иметь место только на границе зоны.

Без учета распределенной емкости

а с учетом этой емкости

где - удельные сопротивления прямой и нулевой последовательностей.

- коэффициенты распространения прямой и нулевой последовательности,

- характеристические сопротивления.

Напряжение , определяемое путем преобразований (*5), (*6), является прогнозируемой величиной и, как правило, не имеет ничего общего с реальным, недоступным измерению напряжением в конце зоны.

Пусть речь идет о защите магистральной ЛЭП. Угол сдвига

по условиям устойчивости не может превышать по абсолютной величине практическиИное дело угол междуи предсказываемой величиной

Когда линия не повреждена, предсказанная величина совпадает с истиной иНо для поврежденной линии преобразования (*5) дадут формальный, хотя и несущий в себе полезную информацию результат, и поскольку при этом, то вполне вероятно, чтопревысита сам угол не поддается предварительной оценке. Так, приотстает от напряженийпочти наи, следовательно, преобразованиедает результат, вообще находящийся в противофазе с величиной. Подобное явление встречается и при иных видах замыканий. Существенно, что взаимное расположение векторовтем не менее не произвольно, а например векторнаходится примежду векторамипричем опережающим может быть как вектортак и

Значения целевой функции для выражения по концам защищаемой для междуфазного КЗ фаз ВС зоны будут равны

где

По аналогии с этими формулами можно записать значения целевой функции по концам зоны идентификации возможного повреждения в защищаемой зоне при .