Лекции по ТБА v3

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

1

Введение

Основными направлениями использования методов ЦО являются циф-

ровая фильтрация и спектральный анализ. Спектральный анализ можно проводить путем вычисления спектров сигналов с помощью дискретного преобразования Фурье (ДПФ) или путем вычисления спектров с примене-

нием статистических методов. На практике при спектральном анализе, как правило, используются быстрое преобразование Фурье (БПФ) и основанная на нем методика вычисления быстрой свертки.

Создание одного за другим нескольких поколений сигнальных процес-

соров Digital Signal Proccessing (DSP) привело к повышению качества вычис-

лительных алгоритмов за счет использования гарвардской архитектуры, кон-

вейеризации процессов, сокращения командного цикла, аппаратной реализа-

ции умножения и т.д. Однако использование в DSP традиционной позицион-

ной арифметики, во-первых, требует увеличения разрядности операндов, что не уменьшает аппаратной затраты и не улучшает отказоустойчивость, во-

вторых, делает желательным наличие режима с плавающей запятой, что по-

тенциально уменьшает быстродействие и требует введения лишних циклов для преобразования целых чисел с плавающей запятой и наоборот; в-третьих,

не снижает стоимости изделий. Наконец, даже в наиболее мощных сигналь-

ных процессорах форматы операндов обеспечивают требуемую точность да-

леко не для всех практических применений.

По-прежнему остро стоят проблемы обеспечения высокой вычисли-

тельной эффективности: уменьшение аппаратных затрат, увеличение быст-

родействия, точности и отказоустойчивости устройств ЦОС. Поэтому в на-

стоящее время актуальны вопросы применения алгоритмических методов улучшения качества вычислительных процедур и, в первую очередь, – теоре-

тико-числовых алгоритмов (ТЧА). Основная идея, заложенная в ТЧА – пере-

индексация чисел во временной последовательности, переход к многомер-

ным процедурам на укороченных выборках данных. Но этот сложный путь не всегда оправдан и часто уступает простым (таким, как БПФ). Поэтому ва-

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

2

жен и актуален второй путь повышения качества ЦОС – непозиционное ко-

дирование сигналов на выходе АЦП. Между непозиционными устройствами кодирования по числам Фибоначчи, в системе остаточных классов (СОК) и

т.п. нет принципиальных отличий. Выводы, которые вытекают из исследова-

ния одой из непозиционных систем (в частности – СОК) распространены на другие. Суть машинной арифметики в системе остаточных классов (СОК) со-

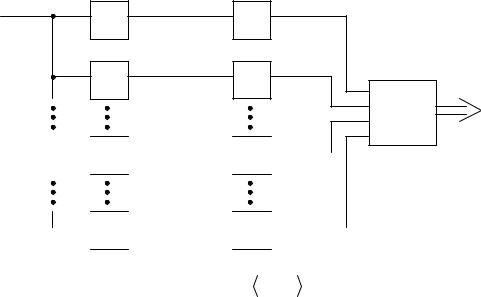
стоит в использовании совокупности неотрицательных вычетов по группе взаимнопростых оснований. Основными узлами непозиционных устройств ЦОС в общем виде являются:

1) Шифраторы Шs, кодирующие входной сигнал x(kT ) числами в

СОК.

2) Спецпроцессоры СПs, обеспечивающие заданный алгоритм обра-

ботки.

3) Дешифратор DS, перекодирующий результат в позиционный код.

Схема цифровой обработки сигналов в СОК

Шs СПs

Шy СПy

Пример. Найти вычет числа 100 по модулю 3.

… – округление в сторону меньшего.

2) rs (kT ) f xs (kT ) , где f – алгоритм ЦОС.

s1

Всовременных устройствах спектрального анализа наибольшее рас-

пространение получили следующие варианты реконфигурации данных для вычисления N-точечных ДПФ, приводящие к синтезу быстрых алгоритмов преобразования:

1. N pt где p 2k, t – целое число, k = 0,1,2. 2. N pt где p 2k 1.

3. N Ns .

s1

Впервом случае чаще других применяется БПФ. Во втором случае для

реализации ДПФ используется алгоритм Рейдера. В третьем случае

N Ns наиболее распространен алгоритм Гуда, преобразующий одно-

s 1

мерный массив в многомерный в соответствии с китайской теоремой об ос-

татках. Алгоритм Гуда уступает БПФ, если вычисляются короткие ДПФ пря-

мым методом. Поэтому используются его разновидности, наиболее эффек-

тивными из которых являются:

1.Алгоритм простых множителей (АПМ), объединяющий алгоритм Гуда и Рейдера.

2.Алгоритм Винограда для ДПФ (АВПФ).

3.Алгоритм поразрядного ДПФ (ПДПФ).

Наименьшую память для хранения программ и данных требует БПФ,

наибольшую АВПФ. В АПМ и АВПФ уменьшено число умножений, но воз-

растает число пересылок. Оценка временных затрат для АПМ, АВПФЫ и БПФ проводилась на моделях микропроцессоров с различными способами выполнения различных операций. При программной реализации операции умножения эффективнее других оказался АВПФ. При аппаратном выполне-

нии умножения БПФ не проигрывает АПМ и АВПФ. Известно, что время пе-

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

4

ресылки данных влияет на производительность не менее, чем умножение.

Поэтому необходимо сделать вывод о том, что БПФ по-прежнему остается одним из самых высокоэффективных вычислительных алгоритмов и на прак-

тике не проигрывает АПМ и АВПФ. В этой связи представляют интерес по-

разрядные алгоритмы ДПФ, число пересылок данных в которых не выше,

чем в БПФ, но большинство сложных операций могут выполняться на этапе проектирования.

Сигналы. Спектральная характеристика.

Периодические сигналы и их представления в виде ряда Фурье.

Условие Дирихле. Спектр периодической функции

При изучении радиотехнических электронных устройств приходится иметь дело с электрическими сигналами, которые связаны с передаваемым общением принятым способом кодирования. Во время передачи по радиоли-

нии сигнал подвергается различным преобразованиям. Одним из наиболее типичных преобразований является модулирование, получаемое в результате модуляции. Высокочастотные колебания, несущие в себе передаваемые со-

общения, называют радиосигналом, а модулирующий сигнал называют управляющим сигналом. Требования к радиотехническому тракту с доста-

точной полнотой могут быть выявлены с помощью двух характеристик управляющего сигнала:

1.спектральная характеристика,

2.распределение уровней.

Спектральная характеристика определяет частотное распределение сигнала. Для детерминированного сигнала спектральная характеристика в общем случае является комплексной функцией частоты. Модули этой спек-

тральной характеристики определяют амплитуды, аргументы – фазы отдель-

ных гармонических составляющих сложного сигнала. Из этого следует, что знание спектральной характеристики сигнала позволяет полосе пропускания

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

5

цепи, а также к равномерности амплитудной и линейной фазовой характери-

стики этой цепи полосе пропускания. Для сигнала, имеющего характер слу-

чайного процесса, спектральная характеристика дает лишь распределение средней мощности по частотам.

Периодическим сигналом является гармоническое колебание, опреде-

ляемое законом:

А

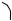t

T

где А – амплитуда, t = ( ; ),

Т– период,

– угловая частота, которая равна 2 или 2 f ,

лера.

Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов, действующих при t ; .

Это представление осуществляется с помощью ряда Фурье (ДПФ).

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

6

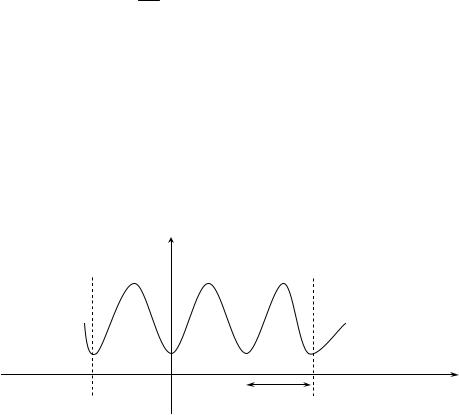
Пусть заданная в интервале t1 t t2 функция S(t) периодически по-

вторяется с частотой 1 2 , где Т – период повторения, причем выполня-

T

ется условие Дирихле:

1. В любом конечном интервале функция S(t) должна быть непре-

рывна или должна иметь конечное число разрыва первого рода, т.е. функция

S(t) и справа и слева должна иметь конечные пределы.

2. В пределах одного периода функция S(t) должна иметь конечное число максимумов и минимумов.

Рис. 2.2.

Подобная функция может быть представлена рядом Фурье, который может быть записан в тригонометрической или комплексной формах:

1.В тригонометрической форме:

2.В комплексной форме:

косинусоидальной и синусоидальной членов разложения S(t). Эти величины определяются по следующим формулам:

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

7

Амплитуда (модуль) и фаза (аргумент) n-ой гармоники выражаются через an и bn следующим образом:

творяют все физически осуществимые сигналы, поэтому для представления периодического сигнала в виде рядов Фурье эти условия на практике не при-

ходится специально оговаривать.

Частные случаи:

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

8

1) В тех случаях, когда сигнал представляет собой функцию четную относительно времени, т.е. S(t) = S(-t). В тригонометрической записи остают-

ся только косинусоидальные члены разложения, т.к. bn 0 в соответствии с формулой (2.6).

2) Функция нечетная относительно времени, то в 0 обращаются ко-

синусоидальные члены разложения.

Структура частотного спектра периодического сигнала полностью оп-

ределяется двумя характеристиками: амплитудной и фазовой, т.е. модулем и аргументом комплексной амплитуды (2.7 и 2.8).

Наглядное представление о ширине спектра и относительной величине его составляющих (гармоник) дает графическое представление спектра пе-

риодического сигнала.

A

2 = 2 1 ,

3 = 3 1 .

По оси ординат – модули амплитуд An . По оси абсцисс – частоты гар-

моник для исчерпывающей характеристики спектра, подобное изображе-

ние должно быть дополнено заданием фаз отдельных гармоник.

Спектр периодической функции состоит из отдельных линий, соответ-

ствующим дискретным частотам: 0, 1, 2 2 1, 3 3 1 и т.д. отсюда и

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

9

название спектра периодического сигнала линейчатый или дискретный

спектр.

Непериодические сигналы

1.Спектральная плотность.

2.Прямое и обратное преобразование Фурье и его свойства.

Пусть задан сигнал в виде функции времени, удовлетворяющей усло-

виям Дирихле, во всяком конечном интервале и абсолютно интегрируемой.

Для проведения гармонического анализа непериодической функции посту-

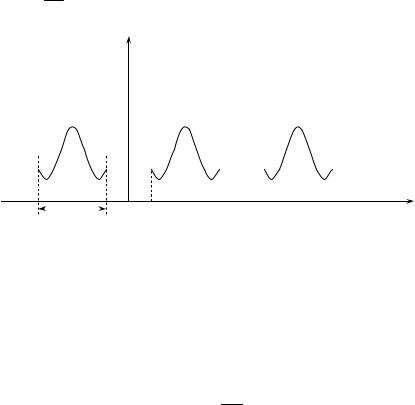
пим следующим образом: превратим заданную функцию в периодическую путем повторения ее с произвольным периодом T t2 t1 . Тогда для этой но-

вой функции применим разложение в ряд Фурье. Причем чем больше T, тем

меньше значение a0 , an, bn , в соответствии с формулами (2.4) и (2.6).

2

S(t)

плитуды гармонических составляющих, сумма которых изображает исход-

ную непериодическую функцию S(t) заданную в интервалах от t1 до t2 . Ко-

личество гармоник входящих в ряд Фурье будет при этом бесконечно боль-

шим, т.к. T основная частота 1 2 0 .

T

Расстояние между отдельными спектральными линиями равно основ-

ной частоте 1 становится бесконечно малым, а спектр, следовательно,

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

10

сплошным. Отсюда следует вывод: при гармоническом анализе непериоди-

ческой функции получается сплошной спектр, состоящий из бесконечно большого количества гармоник, с бесконечно малыми амплитудами. Дока-

жем это математически.

Подставив формулы (2.5) и (2.6) в формулу (2.9) и получим:

Воспользуемся комплексной формой ряда Фурье (2.3) и поставим вме-

сто An в выражение (3.0), получим:

ция суммирования превращается в операцию интегрирования и в результате получаем двойной интеграл Фурье:

; это так называемая спектральная плотность и спектральная характери-

S( )

стика функции S(t). В общем случае, когда неизвестны пределы интегриро-

После подстановки (3.2) в (3.1) получим: