Лекции по ТБА v3

Выражение (3.2) и (3.3) называются прямыми и обратными преобразо-

ваниями Фурье.

Выражение (3.3) представляет непериодическую функцию в виде сум-

мы гармонических колебаний с бесконечно малыми амплитудами.

Поясним смысл спектральной плотности и сравним выражение

S( )

(3.3) с выражением ряда Фурье (2.3). Видно, что амплитуды этих составляю-

щих в случае непериодического сигнала равны: 1

S( )d .

Сравнение выражения (3.2) с выражением (2.11) для комплексной ам-

плитуды составляющей гармоники периодической функции позволяет в

An

наглядной форме пояснить смысл спектральной плотности . Выделив

S( )

какую-либо дискретную частоту n n 1 соответствующее в случае перио-

дической функции n-ой гармоники получим для амплитуды этой гармоники следующее выражение:

В случае непериодической функции совпадающей с соответствующей ей периодической функцией S(t) t1 t t2 получим для спектральной плот-

ности соответствующей той же частоте n следует выражение:

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

спектра, т.е. имеет смысл плотности амплитуд и имеет размерность

амплитуда .

Герц

Из выражения (3.4) вытекает следующее важное положение: огибаю-

щая сплошного спектра непериодической функции (модуль спектральной плотности) и огибающая линейчатого спектра периодической функции сов-

падают по форме и отличаются только масштабом, то

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

13

Очевидно, что модуль и фаза спектральной плотности определяется следующими выражениями:

Как и в случае ряда Фурье модуль S( ) – функция четная, а фаза ( )

– нечетна относительно частоты .

На основании формулы (3.7) нетрудно привести интегральное преобра-

зование (3.3) в тригонометрической форме.

Из упомянутых выше свойств модуля и фазы следует, что подынте-

гральное выражение в первом интеграле является функцией четной, а во вто-

ром интеграле – нечетной.

Следовательно, второй интеграл равен нулю и остается следующее:

Вывод: что, как видно из формулы (3.112) при переходе от комплекс-

ной формы в тригонометрическую, отпадает необходимость интегрирования в области отрицательных значений . Отметим, что интегральные преобра-

зования (3.2)и (3.3) очень удобны для исследования прохождения непериоди-

ческих сигналов через линейные цепи. Прикладное значение этих преобразо-

ваний, позволяющих осуществить гармонический анализ непериодических сигналов еще более велико, чем значение радов Фурье, т.к. непериодические сигналы встречаются на практике чаще чем периодические.

Свойства преобразования Фурье

Из рассмотрения прямого и обратного преобразования Фурье можно сделать некоторые общие заключения о характере, спектральной плотности

S( ) при заданной функции S(t) и наоборот. Если в обратном преобразова-

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Это означает, что если всем составляющим спектра функции S(t) дать

фазовый сдвиг t0 , линейно связанной с частотой , то функция S(t)

сдвигается во времени на t0 . Очевидно и обратное положение. Сдвиг во времени функции S(t) на величину t0 означает изменение фазовой харак-

теристики спектральной плотности S( ) на величину t0 .

Из указанных свойств Фурье, вытекают следующие требования к ли-

нейным системам, выполнение которых необходимо для неискаженной пере-

дачи сигналов.

Требования:

1)АЧХ системы должно быть равномерно;

2)ФЧХ линейна в пределах всего спектра сигнала.

Обратимся теперь к рассмотрению S( ) для различия функций:

1. пусть S(t) – функция четная относительно t . Переписав выраже-

ние (3.1) в виде:

и убеждаемся, что при четной S(t) второй интеграл равен нулю. следова-

тельно делаем вывод, что в этом случае функция S( ) – функция вещест-

венная и четная относительно .

2. Пусть S(t) – нечетная функция относительно t . То первый инте-

грал равен нулю. И получим:

S( ) i S(t)sin tdt

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

15

Следовательно, в этом случае S( ) – нечетная и чисто мнимая функция.

3. Если S(t) – функция является ни четной, ни нечетной. То тогда

S(t) можно разложить на две функции S1(t) – четная и S2 (t) – нечетная.

Вывод: функция S( ) представляет собой комплексную функцию .

Из первого случая вытекает, что в случае четной функции S(t) выра-

жение (3.1) можно произвольно изменять знак перед .

Следовательно, в этом случае интегралы выражения (3.1)и (3.2) совер-

шенно подобны. И переменные и t взаимно заменимы. Из этого следует,

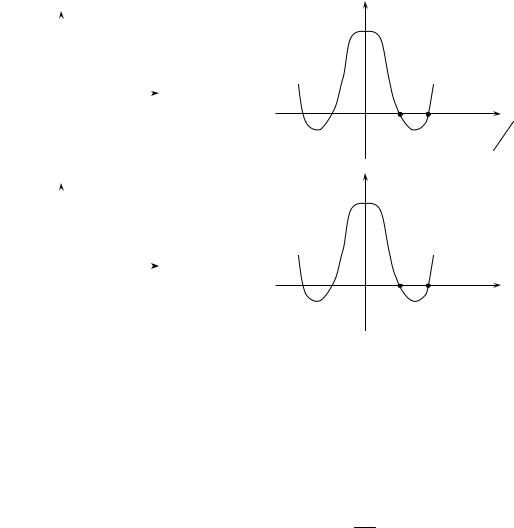
что если прямоугольному импульсу S(t) рис. а соответствует спектр пока-

S( ) можно считать почти неизмененным, то (рис. г) непосредственно ха-

рактеризует искажения, претерпеваемые прямоугольным импульсом при от-

брасывании всех частот вне полосы 0 1 (при 2 ).

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

16

Дискретные сигналы. Дискретное преобразование Фурье (ДПФ).

Алгоритм БПФ с основанием 2

В случае непрерывных сообщений теория информации строится на за-

мене этих сообщений эквивалентной им по информационному содержанию совокупностью дискретных сигналов.

Операция такой замены, которую будем называть дискретизацией не-

прерывного сигнала, основывается на теореме отсчетов (Котельникова).

Теорема Котельникова: если функция S(t) не содержит частот свыше

Fm гц., то она полностью определяется последовательностью своих значений

в моменты, отстоящих друг от другу на 1 сек.

2Fm

Итак, непрерывный сигнал S(t) полностью определяется дискретной последовательностью своих значений, отсчитанных через интервалы време-

ни, равные 1 . Эти значения функции называют выборками сигнала.

2Fm

Дискретные сигналы определяются лишь для дискретных значений не-

зависимой переменной – времени. Обычно время квантуется равномерно, т.е. t nT , где T – интервал между отсчетами. Математически дискретные сиг-

налы представляются в виде непрерывной последовательности чисел. Для описания последовательностей может быть использовано одно из следующих обозначений:

a){ x(n) }, N1 n N2

b){ x(nT) }, N1 n N2

c)x(n), N1 n N2

d)x(nT), N1 n N2

а) и с) используются при неравномерном расположении отсчета, b) и d)

– при равномерном.

Обычно для получения последовательностей методом дискретизации непрерывных колебаний используют АЦП.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

17

На приведенных ниже рисунках изображены некоторые важные после-

довательности, часто используемые при ЦОС.

Особенно важной последовательностью является комплексная экспо-

нента e j n cos( n) jsin( n) . Поскольку эта последовательность является комплексной, то для изображения необходимо два рисунка: действительной и мнимой части.

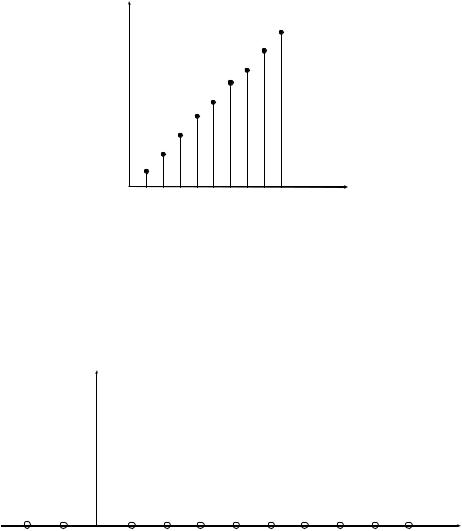
а) x(n) = n, 0 n N-1

x(n)

б) Цифровой единичный импульс.

1, n 0

x0 (n)

0, n 0

(аналогично s(t) в аналоговой системе).

x0(n)

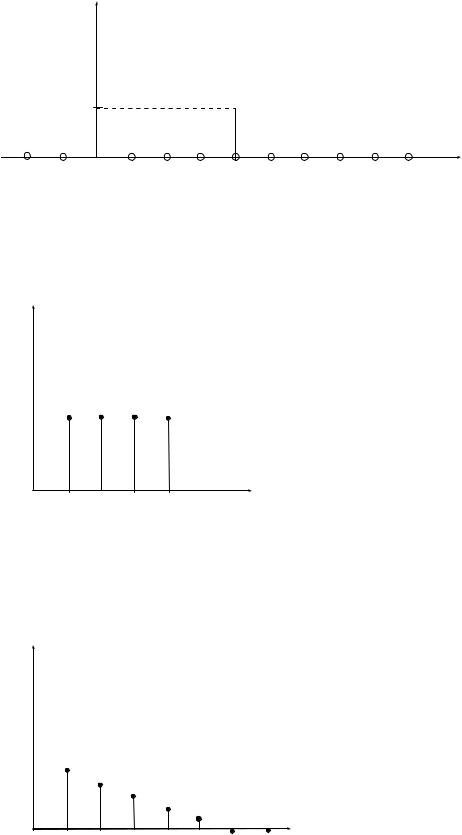
в) Единичный импульс, задержанный на n0 отсчетов.

1, n n0 x0 (n n0 )

0, n n0

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

18

x0(n-n0)

1

г) Единичный скачек

1, n 0

x 1 (n)

0, n 0

x-1(n)

д) Убывающая экспонента

xn , n 0

g(n) x 0,70, n 0

x-1(n)

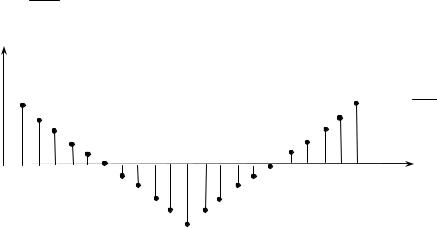
е) Косинусоида

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

19

h(n) cos(2 n) n0

cos( 0n)

( 0 2 ) 16

0 1 2

Дискретное преобразование Фурье

В тех случаях, когда последовательность периодична, ее можно пред-

ставить рядом Фурье. Итак, рассмотрим периодическую последовательность

X p (n) с периодом в N отсчетов.

гут принимать только значения k 2kл / N , где k ( ; ) , так как перио-

ды других частот некратны N.

В равенстве (4.2) коэффициенты X p (k) представляют амплитуды си-

нусоид с частотами k . Запись (4.2) избыточна вследствие периодичности функции e j . Исходя из этого, после ряда математических преобразований можно записать формулу (4.2) в виде (4.3):

n 0

Соотношение (4.4) носит название ДПФ, а (4.3) – ОДПФ (обратного дискретного преобразования Фурье).

Формулу (4.4) можно записать в более удобной форме:

Generated by Foxit PDF Creator © Foxit Software

где X (k) – k-ая гармоника спектра для чисел x(n); W – весовая функция

W e j(2 / N )kn .

Свойства ДПФ

1. Линейность.

Если xp (n) и yp (n) периодические последовательности с периодом в N

отсчетов каждое, а X p (k) и Yp (k) их ДПФ, то ДПФ последовательности

xp (n) + yp (n) = X p (k)+Yp (k). Это положение справедливо для последова-

тельности конечной длины.

2. Сдвиг.

Если последовательность xp (n) периодическая с периодом в N отсче-

тов, а ее ДПФ равно X p (k), то ДПФ периодической последовательности ви-

Таким образом, с точки зрения ДПФ последовательность xp (n n0 ) по-

лучается путем кругового сдвига элементов последовательности xp (n) на n0

отсчетов.

3. Свойство симметрии.

Если периодическая последовательность xp (n) с периодом в N отсче-

тов является действительной, то ее ДПФ X p (k) удовлетворяет следующим условия симметрии:

Re X p (k) Re X p (N k)

Im X p (k) Im X p (N k)

X p (k) X p (N k)

arg X p (k) arg X p (N k)