
Лекции по ТБА v3
.pdfGenerated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
21
Последовательность x(nT ) или x(n) получается путем дискретизации непрерывного колебания x(t) с периодом T. Пара преобразований Фурье для непрерывного колебания имеет вид функции (3.2) и (3.3).
Аналогичные соотношения для дискретизированного колебания с пе-
риодом в N отсчетов, т.е. T 2 / N . В этом случае формулы (4.3) и (4.4).
Быстрое преобразование Фурье (БПФ)
При обработке сигнала во многих случаях приходится измерять спек-
тры. Например: в задачах распознавания речи, гидроакустических системах,
в радиолокационных системах.
Набор алгоритмов называемых алгоритмами БПФ включает разнооб-
разные методы уменьшения времени вычисления ДПФ. Поскольку вычисле-
ние ДПФ является основной операцией в большинстве задач спектрального анализа, то использование БПФ в некоторых встречающихся на практике случаях, позволяющее увеличивать скорость вычисления ДПФ в 100 и более раз, по сравнению с методом прямого вычисления ДПФ, имеет чрезвычайно важной значение и должно рассматриваться как неотъемлемая часть приме-
нения методов ЦОС для спектрального анализа. Поэтому вначале рассмот-
рим теорию БПФ, включающую хорошо известные алгоритмы с основанием
2 и прореживанием по времени и по частоте. Далее покажем, каким образом можно представить БПФ в виде единого алгоритма, имеющего много различ-
ных вариантов. Тот факт, что одномерный массив чисел можно выразить че-
рез двумерный массив более чем одним способом, объясняет многообразие алгоритмов БПФ. Отсюда следует, что математическая операция перехода из одномерного пространства в двумерное является основой для всех алгорит-
мов БПФ.
Алгоритмы БПФ с основанием 2
Известно, что ДПФ конечной последовательности x(n) , 0 n N 1
определяется по формуле (4.4'):
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
22
N 1
X (k) x(n)W nk , где W e j(2 / N )kn .
n 0
Легко показать, что W nk является периодической последовательностью с периодом N. Часто периодичность W nk подчеркивают тем, что вместо W
записывают WN .
Из соотношения (4.4') следует, что прямом вычислении ДПФ на N точек нужно выполнить (N 1)2 комплексных умножений, и N(N-1) сложений. Та-
ким образом, для достаточно больших N (1000 и более) прямое вычисление ДПФ требует чрезмерного количества вычислительных операций. Основная идея БПФ состоит в том, чтобы разбить исходную N – точечную последова-
тельность на две более короткие последовательности, ДПФ которых может быть скомбинирован таким образом, чтобы в итоге получить ДПФ исходной
N-точечной последовательности. Например, если N – четное, а исходная N –
точечная последовательность разбита на 2 N/2 точечные последовательности,
то для вычисления искомого N-точечного ДПФ потребуется N / 22 2 N 2 / 2
комплексных умножений, т.е. в 2 раза меньше по сравнению с прямым вы-
числением. Здесь множитель (N / 2)2 даст число умножений, необходимых для прямого вычисления для прямого вычисления (N / 2) точечного ДПФ, а
множитель 2 соответствует двум ДПФ, которые были вычислены. Эту опера-
цию можно повторить вычисляя вместо (N / 2) - точечного ДПФ два (N / 4) -
точечных ДПФ. Предполагая, что (N / 2) – четное число и сокращая таким образом объем вычислений еще в 2 раза. Выигрыш в 2 раза является прибли-
женным, т.к. не учитывается, каким образом, из ДПФ меньшего размера об-
разуется искомое N –точечное ДПФ.
Проиллюстрируем описанную методику для N – точечной последова-
тельности x(n) , считая, что N равно степени.
Введем две (N / 2) – точечные последовательности x1(n) и x2 (n) из четных и нечетных членов x(n) соответственно, т.е.:

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
|
|
|
23 |
|
|
|
|
|
x1 |
(n) x(2n), |
n 0,1..., |
N |
1 |
|
|||
|
|
|||||||
|
|
|
2 |
|
N |
(4.5) |
||
|
|
|
|
|
|
|||
x 2 |
(2) x(2n 1), |
n 0,1,..., |
1 |
|||||
|
||||||||
|
|
|
|
|
2 |
|
||
N – точечное ДПФ последовательности x(n) можно записать следую-
щим образом:
|
|
|
|
|
N 1 |
|
|
|
|
|
N 1 |
|
|
|
|
X (k) x(n) WNnk x(n) WNnk |
|||||||||||||||
|
|
|
|
|
n 0 |
|
|
|
|
|
n 0 |
|
|
|
|
|
N |
2 |
1 |
|
|
|
|
|
N |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x(2n) WN2nk |
|
x(2n 1) WN(2n 1)k |
||||||||||||
|
n 0 |
|
|
|
|
|
|
n 0 |
|
|
|
||||
С учетом того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
j(2 |
|
) |
j |
|
|
|
|||
W |
|
e |
N |
e |
|
|
(N |
) |
W |
|
|||||
N |
|
|
|
|
|
2 |
|
N |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
перепишем выражение (4.7) в виде:
(4.6)
(4.7)
(4.8)
|
|
|
|
|
|
N |
1 |
|
N |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
X (k) x1(n) WNnk WNk |
x2 (n) WNnk |
(4.9) |
|
|||||
|
|
|
|
|
|
n 0 |
2 |
n 0 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
X (k) X1(k) WNk X 2 (k) |
|
|
|
(4.10) |
|
|||
где |
X |
(k) |
и |
X |
2 |
(k) равны |
|
N |
-точечным ДПФ последовательностей |
x (n) |
и |
|||
|
|
|||||||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 (n) . Из формулы (4.10) |
следует, что N-точечное ДПФ X (k) может быть |
|||||||||||||
разложено на два N -точечных ДПФ, результаты которых объединяются со-
2
гласно (4.10). Если бы N -точечные ДПФ вычислялось бы обычным спосо-
2
бом, то для вычисления N-точечного ДПФ потребовалось бы, очевидно,
N 2 2 N комплексных умножений. При больших N (когда N 2 2 N ) это позволяет сократить время вычисления на 50%.

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
24
Формулу (4.10) нужно доопределять для k N 2 . Это определение дос-
таточно очевидно (из-за периодичности ДПФ) и может быть записано сле-
дующим образом:
X |
(k) W k X |
2 |
(k), |
|
0 k N |
2 |
1 |
|
|||
|
1 |
N |
|
|
|
|
|
|
|||
X (k) |
|
(k N |
) W k X |
|
(k N |
), |
|
N |
k N 1 |
||
X |
2 |
|
|||||||||
|
1 |
2 |
|
|
N |
2 |
|
|
2 |
|
|
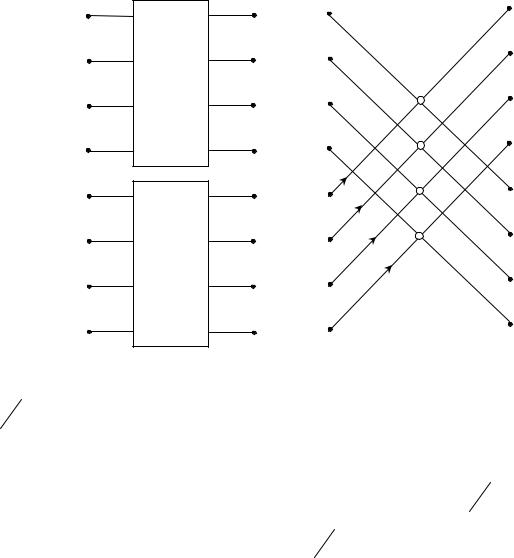
На рис. 4.2 с помощью направленного графа представлена последова-
тельность операций при выполнении восьмиточечного ДПФ с использовани-
ем двух четырехточечных преобразований. Входная последов x(n) сначала разбивается на две последовательности x1(n) и x2 (n) из четных и нечетных членов x(n) , после чего рассчитываются их преобразования X1(k) и X 2 (k).
Затем в соответствии с формулой (4.11) получают X (k) . Не закрашенные кружки в правой части рис. 4.2 обозначает операцию сложения (вычитания),
причем верхний выход соответствует сумме, а нижний – разности.
a a+b
сложение, вычитание
b |
a-b |
а W k |
а W k умножение |
На рис. 4.2 с помощью направленного графа представлена последова-
тельность операций при выполнении 8-точечного ДПФ (N = 8) с использова-
нием двух четырехточечных преобразований.
Входная последовательность x(n) сначала разбивается на две последо-
вательности x1(n) и x2 (n) из четных и нечетных членов последовательности x(n) , после чего рассчитываются их преобразования ДПФ – X1(k) и X 2 (k), а
затем в соответствии с формулой (4.11) получим ДПФ – X k входной по-
следовательности x(n) .
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
25
x (0) x(0) |
X |
1(0) |
X (0) |
|
|||
1 |
|
|
|
x (1) x(2) |
4-х |
X1(1) |
X (1) |
|
|||
1 |
точечное |
|
|
|
|
|
x (2) x(4) |
ДПФ |
X1(2) |
|
|
|
X (2) |
||
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
x (3) x(6) |
|
X1(3) |
|
|
|
X (3) |
||
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
x2 (0) x(1) |
|
X 2 (0) |
W |
0 |
|
X (4) |
||
|
W 1 |
|
|
|||||
x |
|
(1) x(3) |
4-х |
X 2 (1) |
|
|
X (5) |
|
2 |
|
W 2 |
|
|
||||
|
|
точечное |
|
|
|
X (6) |
||
x2 (2) x(5) |
ДПФ |
X 2 (2) |
|
W |
3 |
|||
|
|
|
|
|||||
x2 (3) x(7) |
|
X 2 (3) |
|
|
|
X (7) |
||
|
|
|
|
|
||||
Рассматриваемая схема вычислений может быть использована для рас-
чета N 2 -точечного ДПФ в соответствии с формулами (4.10) и (4.11). Любая
из последовательностей x1(n) и x2 (n) разбивается на две последовательно-
сти, состоящие из четных и нечетных членов. Аналогично N |
2 |
-точечные |
|||||||
|
|
|
|
|
|
|
|
|
|
ДПФ могут быть записаны как комбинации N |
-точечных ДПФ, т.е. |
||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
X1(k) A(k) WNk B k |
|
|
(4.12) |
||||
|
2 |
|
|
|
|
|
|
||
|
|
X1(k) A(k) WN2k B(k) |
|
|
(4.13) |
||||
где k 0,1,..., |
N |
1, а A(k) и B(k) – |
N |
-точечные ДПФ соответственно |
|||||
|
2 |
||||||||
2 |
|
|
|
|
|
|
|
||
четных и нечетных членов x1(n) .
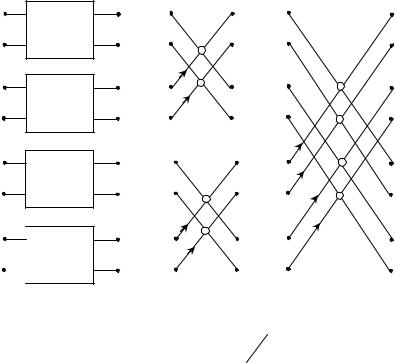
На рис. 4.3 показан результирующий направленный граф, в котором 4-
точечные ДПФ из рис. 4.2 засчитываются согласно формуле (4.13).
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
26
a(0) x1(0) |
x(0) |
2-х |
A(0) |
|
|
|
X1(0) |
|
X (0) |
a(1) x1(2) |
x(4) |
точечное |
A(1) |
|
|
|
X1(1) |
|
X (1) |
ДПФ |
|
|
|
|
|||||
b(0) x1(1) x(2) |
2-х |
B(0) |
W |
0 |
X1(2) |
|
X (2) |
||
точечное |
|
2 |
|
||||||
b(1) x2 (3) |
x(1) |
B(1) |
W |
X1(3) |
|
X (3) |
|||
ДПФ |
|
|
|
|
|||||
c(0) x2 (0) x(1) |
2-х |
C(0) |
|
|
|
X 2 (0) W 0 |
|
X (4) |
|
c(1) x2 (2) |
x(5) |
точечное |
C(1) |
|
|
|
X 2 (1) W 1 |
|
X (5) |
ДПФ |
|
|
|
2 |
|||||
|
|
|
|
|
|
|
W |
|
|
d (0) x2 (1) |
x(3) |
2-х |
||
d (1) x2 (3) |
x(7) |
|
|
точечное |
|
|
ДПФ |
||
|
||||
D(0) W 0 |
X 2 (2) W 3 |
X (6) |
|
D(1) |
W |
2 |
X (7) |
|
X 2 (3) |
||
Рис. 4.3
Процесс уменьшения размера ДПФ от L до L 2 , где L = степени 2, мо-
жет быть продолжен до тех пор, пока не останутся только 2-х точечные ДПФ. 2-х точечное ДПФ F(k), k 0,1, может быть рассчитано без использования операции умножения по формуле (4.14).
F(0) |
f (0) f (1) W 0 |
|
|
|
|
8 |
(4.14) |
|
|
4 |
|
|
|
|
|
F(1) |
f (0) f (1) W8 |
|
|
В этой формуле f (n), n 0,1 |
преобразуемая 2-х точечная последова- |
||
тельность. Поскольку W 0 1 и |
W 4 |
1, то для формулы (4.14) действитель- |
|
8 |
8 |
|
|
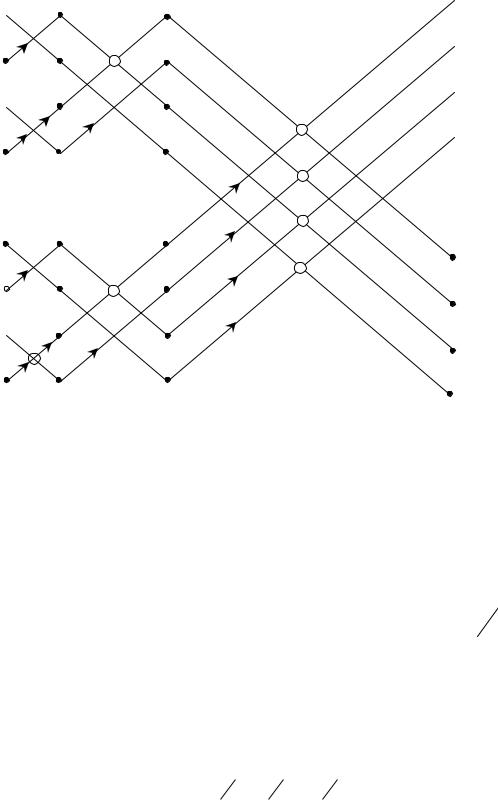
но не нужны операции умножения, таким образом 8-точечное ДПФ в итоге сводится в алгоритму, описываемому направленным графом, представлен-
ным на рис. 4.4.
Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.
27
x(0) 
W0
x(4)
x(2)  W0
W0
W0
x(6)
a |
b
c W2 
 d
d
 X(0)
X(0)
A
 X(1)
X(1)
B
 X(2)
X(2)
C
 X(3)
X(3)
D
W0
x(1)
e
W0
x(5) 
f
x(3)  W0 g W2
W0 g W2 
W0 
x(7)
h
W1
E |
X(4) |
|
|
||
F |
W2 |
|
X(5) |
||
|
||
G |
W3 |
|
X(6) |
||
|
||
H |
X(7) |
|
|
Рис. 4.4. 8-точечное ДПФ полученное последовательным
прореживанием в 2 раза
Свойства алгоритма БПФ с основанием 2
и прореживанием по времени
Анализ графа на рис. 4.4 и процедуры последовательного сокращения вдвое размеров преобразований показывает, что на каждом этапе БПФ (т.е.
при каждом сокращении размеров ДПФ) необходимо выполнить |
N |
ком- |
|||||
|
|
|
|
|
|
2 |
|
плексных умножений. Так как общее количество этапов log2 N , |
то число |
||||||
комплексных умножений необходимое для нахождения N -точечного ДПФ |
|||||||
примерно равно |
N |
log2 N . |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
N |
N |
3N |
|
|
|
Так как умножения на WN0 ,WN |
2 ,WN |
4 ,WN |
4 в действительности сво- |
||||
дится к сложению и вычитанию комплексных чисел.
Например, на рис. 4.4 первый этап БПФ содержит только операции сложения и вычитания. На втором этапе тоже используется только сложение
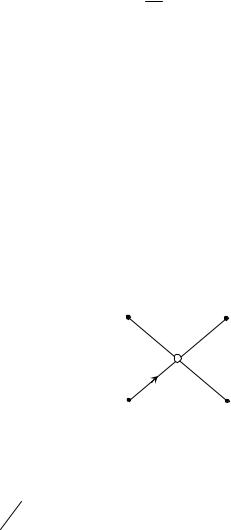
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
28
и вычитание. Фактически, как следует из рис. 4.4 вместо ожидаемых 12 ум-
ножений достаточно выполнить только 2 умножения.
Однако, для большинства значений N фактическое число умножений
апроксимируется формулой N log2 N . Описанный алгоритм называется ал-
2
горитмом с прореживанием по времени.
Поскольку на каждом этапе входная (т.е. временная) последователь-
ность разделяется на 2 обрабатываемые последовательности меньшей длины,
т.е. входная последовательность прореживается на каждом этапе. Базовая операция с прореживанием по времени имеет вид:
|
|
k |
B |
|
X |
A WN |
|
|
|
k |
(4.15) |
|
|
B |
|
|
Y |
A WN |
|
называется «бабочка». |
|
|
|
А |
|
|
k |
|
|
X A B WN |
|
В |
WNk |
Y A B WNk |
|
«Бабочка» – базовая операция алгоритма БПФ.
Рассмотрение графа на рис. 4.4 показывает, что каждый из этих этапов
содержит |
N |
базовых операций. В случае, когда множитель W k |
нетриви- |
|
2 |
N |
|
альный, для каждой базовой операции необходимо выполнить только одно умножение, так как величину B WNk можно вычислить и запомнить. Таким образом структура базовых операций такова, что для выполнения БПФ N -
точечной последовательности, размещенной в памяти необходимо иметь лишь одну дополнительную ячейку памяти. Результаты всех промежуточных этапов БПФ можно размещать в те же самые ячейки памяти, где находилась исходная последовательность x(t) . Поэтому для хранения и входной и вы-
ходной последовательности можно использовать один и тот же массив ячеек памяти. Алгоритм, в котором для размещения входных и выходных последо-
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
29
вательностей используются одни и те же ячейки памяти, называется алго-
ритмом БПФ с замещением.
Из рис. 4.4 следует, что N -точечная БПФ содержит log2 N этапов,
причем все операции умножения используются только при объединении ре-
зультатов ДПФ. Поскольку эти умножения используются во всех алгоритмах БПФ, соответствующие множители получили специальное название повора-
чивающих множителей.
Еще одной особенностью алгоритма с прореживание по времени явля-
ется необходимость такой перестановки элементов входной последователь-
ности, чтобы входная последовательность X (k) имела естественный (пря-
мой) порядок расположения, т.е. k 0,1...N 1. ( В примере на рис. 4.4 для
этого требуется следующий порядок размещения входной последовательно-
сти x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7) ).
Характер перестановки элементов входной последовательности может быть описан сравнительно просто. В том случае, когда N является степенью
2, входная последовательность должна быть расположена в памяти в двоич-
но-инверсном порядке, для того, чтобы выходная последовательность полу-
чалась в прямом порядке.
Если записать порядковые номера элементов входной последователь-
ности в двоичном коде используя L двоичных разрядов, причем N 2L , а
затем инвертировать порядок следования разрядов, то получаемые при этом числа и будут номерами элементов входной последовательности после их пе-
рестановки.
Номер |
Двоичное |
Двоичная |
Двоично-инверсный |
|
представление |
инверсия |
номер |
||
|
||||
|
|
|
|
|
0 |
000 |
000 |
0 |
|
1 |
001 |
100 |
4 |
|
2 |
010 |
010 |
2 |
|
3 |
011 |
110 |
6 |
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
||
|
|
http://www.foxitsoftware.com |
For evaluation only. |
|
|
|
30 |
|
|
|
|
|
|
|
4 |
100 |
001 |
|
1 |
5 |
101 |
101 |
|
5 |
6 |
110 |
011 |
|
3 |
7 |
111 |
111 |
|
7 |
|
|
|
|
|
Еще одна особенность алгоритма БПФ заключается в том, что на всех этапах преобразования используются коэффициенты WNk , k 0,1...N 1.
Существует несколько способов получения этих коэффициентов. Са-
мый простой способ: составление таблицы, к которой можно обращаться в процессе счета. Недостаток: дополнительная память, что при больших N
становится проблематично.
Второй способ заключается в непосредственном вычитании коэффици-
ентов WNk .
W k |
|
|
2 |
|
|
|
2 |
|
|
||
cos |
|
|
k |
|
jsin |
|
|
k |
|
. |
|
|
|
||||||||||
N |
|
|
N |
|
|
N |
|
||||
|
|
|
|
|
|
|
|
||||
С использованием каждый раз стандартных подпрограмм расчета сину-
са и косинуса. Этот способ требует много времени.
Третий способ основан на применении простой рекуррентной формулы:
W k |
W k L W k |
…… |
..(4.16) |
|
N |
N |
N |
|
|
L – число двоичных разрядов. |
|
|
|
|
С начальным условием, что WN0 1, |
т.к. степени |
N на каждом этапе |
||
БПФ меняется с постоянным шагом. Например, на рис. 4.4 на первом этапе используются коэффициенты: W 0 ,W 4 ; на втором: W 0 ,W 2 ,W 4, W 6 ; и на третьем шаге: W k , k 0,1...7.
Поэтому, чтобы иметь возможность на каждом из этих этапов исполь-
зовать формулу 4.16 достаточно запомнить или вычислить только множители
W 4 ,W 2 ,W 0 .
Приведем таблицу сравнений числа операций при прямом вычислении ДПФ и при использовании алгоритма БПФ при N от 2 до 2048.
