3. 7.2.2.4 Прямые целевые функции

Целевая функция безразлична к составу пассивного многополюсника повреждения. В этом есть определенное удобство, однако здесь не удается использовать дополнительную информацию, имеющуюся при однофазном и двухфазном повреждениях.

При неполнофазных повреждениях общие целевые функции упрощаются (см. табл. 2 и 3).

Критерий реактивной мощности представляет наибольший интерес, так как он инвариантен к видам замыкания. Важен лишь тот факт, что само повреждение резистивно и его реактивная мощность равна нулю.

Таблица 2.

	Целевая функция
	Прямая	Косвенная
К(1)
К(2)
К(1,1)
К(3)

Таблица 3.

Замыкание	Приближенные соотношения
К(1)
К(2)
К(1,1)
К(3)

При в точкевыполняются следующие соотношения:

каждое из которых может служить критерием определения координаты

Целевые функции, дающие правильные, т.е. свободные от методической погрешности, результаты при различном повреждении фаз называют прямыми. Так при выявлении повреждения в фазе А целевая функция запишется в виде

Если же при этом используется трехфазный параметр , то в точкедействия всех критериев объединяются, и следует ожидать при этом более точного результата ОМП.

Расчет функций требует определения поперечных токов, что предопределяет знание параметров, но если известен вид замыкания, то при записи критерия можно учесть соотношения между симметричными составляющими, хотя очевидно, что привлечение дополнительных признаков замыкания снижает крутизну функциивблизи точки

Все приведенные целевые функции названы в таблице прямыми по той причине, что они предполагают определение токов предполагаемого повреждения как функций . Но этого нельзя сделать при неопределенных параметрахДанное обстоятельство побуждает обратиться к косвенным целевым функциям, обходящимися легко определяемыми токами

4. 7.2.2.5. Косвенные целевые функции

Алгоритмы, базирующиеся на косвенных целевых функциях, не свободны от методической погрешности и не могут обойтись без предварительного определения вида КЗ. Эта группа алгоритмов подразделяется на две группы:

- использующие информацию о предшествующем режиме. Они более эффективны, но и более сложны. Алгоритмы этой группы используют аварийные токи;

- более простые, но и менее точные алгоритмы обходятся только после коммутационными величинами.

Косвенные целевые функции основаны на фазовых соотношениях между токами повреждения и симметричными или безнулевыми составляющими токовТоки нулевой и обратной последовательностей растекаются из места повреждения по левой и правой частям с относительно слабым изменением фазы. Если предположить, что влияние активных сопротивлений неощутимо, а в предшествующем режиме нулевой и обратной последовательностей не было, то

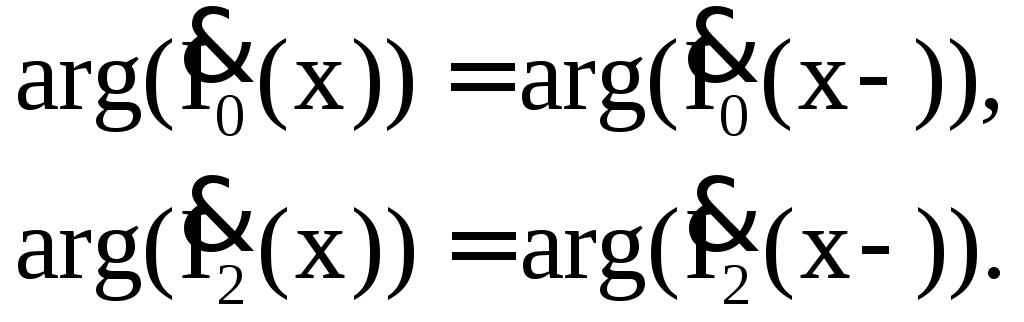(2*)

К указанным соотношениям добавим уравнения для безнулевых токов

5. 7.2.2.6. Граничные условия в месте повреждения

Как уже отмечалось, косвенные критерии опираются на предварительное определение поврежденных фаз и вида повреждения. Рассмотрим фазовые соотношения для различных видов повреждения.

1. Граничные условия при

Рисунок. а) Модель и б) векторная диаграмма однофазного КЗ на землю.

В месте повреждения

т.е. или,

тогда из (2*) следует

или

Аналогично для безнулевой слагаемой

и

2. Граничные условия при

Взаимосвязь между токами прямой и обратной последовательности в самом повреждении

приводит к выражению

а совместно с (2*)

Рисунок. а) Модель и б) ВД междуфазного КЗ

К тому же при этом виде КЗ

и

3. Граничные условия при

Из разных модификаций данного вида КЗ остановимся на более общей модели с тремя резисторами. Здесь соотношение

совместно с (2*) дает

В той же схеме и

Рисунок. Модель двухфазного КЗ на землю.

4. Граничные условия при

Здесь можно рассчитывать только на привлечение данных о предшествующем режиме, те.

Модель трехфазного КЗ на землю:

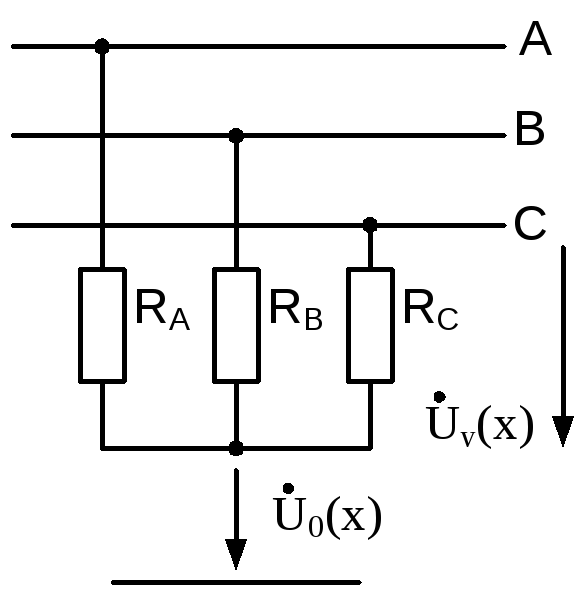
Рисунок. Модель трехфазного КЗ на землю