2. Целевые функции и критерии

   1. 7.2.2.1 Классификация целевых функций

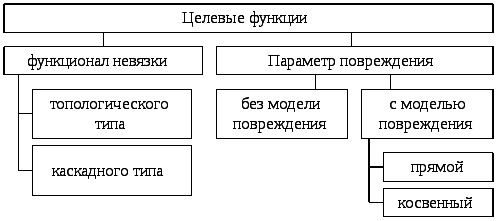
АДП по определению предполагает решение оптимизационной задачи, в ходе которого используются целевые функции. Систематизация модификаций оптимизационного алгоритма выявило два класса целевых функций: типа функционала невязки и типа параметра повреждения.

Информация о трехфазной цепи, включающей в свой состав симметричную линию более многообразна. К информационным факторам могут быть отнесены симметричные составляющие напряжений и токов, учитывая при этом, что, за исключением отдельных случаев, в переходных величинах невозможно разграничить прямую и обратную последовательность.

Величины, остающиеся после удаления нулевой последовательности названы безнулевыми. В системе нулевой и безнулевых составляющих могут быть построены комплексные схемы замещения, каждая из которых отвечает граничным условиям, присущим конкретным КЗ. Т.о. получается, что информацию о состоянии ЛЭП несут в первую очередь нулевая и три безнулевые составляющие токов и напряжений, а затем уже спектральные компоненты каждой из них.

Первый пригоден для любой схемной модели и любой модели повреждения, в том числе и нелинейной, но при условии, что структура повреждения задана. В зависимости от того, какой метод применяется для расчета схемной модели, различают алгоритмы на основе топологического или каскадного анализа. В первом случае целевая функция имеет вид

где - рассчитанные отсчеты входного напряжения и тока, полученные из схемной модели при подаче на нее наблюдаемых токов. Критерием же определения места повреждения служит условие достижения целевой функцией глобального минимума на множестве варьируемых параметров.

Во втором случае целевая функция имеет вид

где - напряжения, определенные по формуле каскадного соединения,

- оператор приемной системы

что для комплексов означает

7.2.2.2. Целевые функции типа параметра повреждения

Целевые функции типа параметра повреждения основываются на резистивной природе повреждения. Соответственно внутри этого класса целевых функций выделено два подкласса: общий, не связанный с моделью повреждения, и частный, предполагающий ее введение. В роли целевых функций, так или иначе, выступают некоторые реактивные параметры, принимающие нулевое значение в месте повреждения.

Эта закономерность наводит на мысль о целевой функции илина базе реактивной мощности повреждения, предполагаемого в произвольной точкеx. На основной гармонике целевая функция выглядит

U, I – напряжение и ток поперечной ветви.

2. 7.2.2.3. Целевая функция для определения зоны и места повреждения лэп

Общий критерий идентификации повреждения в ЛЭП заключается в требовании

а конкретнее

или можно воспользоваться более простым критерием

Поведение функций представляет в этом плане особый интерес. Функции типа реактивного параметра повреждения с увеличениемх обладают свойством: переходя через точку повреждения, они изменяют знак с положительного на отрицательный :

или наоборот.

Свойство целевой функции иметь разные знаки по концам защищаемой зоны создает предпосылки для реализации дистанционных принципов защиты. Соответствующий подход к построению ДЗ получил название метода дистанционных критериев.

Докажем, что функция переходит через ноль в единственной точке. Поясним сказанное простейшим примером КЗ в двухпроводной ненагруженной линии с односторонним питанием.

Рассмотрим линию на ХХ:

ИМО для нее:

Для этой линии

При КЗ вне зоны условие (*) в линии не выполняется:

Если же КЗ произошло «за спиной» (), то в данном случаеИз данного простейшего примера можно сделать предварительный вывод о том, что анализ целевой функции и, в частности, законовпредотвращает неселективное поведение алгоритма. Заметим, что свойствопри КЗ «за спиной» органически присуще этому алгоритму. Дело в том, что уравнения схемной модели, привлекаемые для определения токов повреждения, адекватно отображают состояние неповрежденной линии при замыкании слева от точки наблюдения и, поэтому дадут расчетные токи, откуда следует, что при всехх токи будут нулевого уровня.