
- •Розділ 1. Теорія множин.
- •1. Основні означення теорії множин.
- •2. Дії над множинами.
- •3. Алгебра множин.
- •Розділ 2. Вектори, відношення, відображення.
- •1. Вектори і прямий добуток множин.
- •2. Відношення.
- •Відображення.
- •4. Функції.
- •5. Перетворення.
- •6. Сукупність підстановок множини м: s(м).
- •7. Алгебраїчні операції та системи.
- •Розділ 3. Алгебра логіки.
- •1. Висловлення.
- •2. Основні логічні операції.
- •3. Основні закони алгебри логіки.
- •4. Логічна функція.
- •5. Бульові функції.
- •Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми.
- •1. Диз’юнктивні нормальні форми.
- •1) Елементарний добуток
- •2) Диз`юнкція різних елементарних добутків відносно
- •3) Тотожна хибність.
- •2. Досконала диз’юнктивна нормальна форма. (дднф)
- •3. Скорочена днф.
- •1. Імпліканта.
- •2. Скорочена днф.
- •4. Мінімізація логічних функцій методом Квайна.
- •5. Кон’юнктивні нормальні форми.
- •6. Мінімізація логічних функцій за допомогою таблиць Вейча.
- •7. Мінімізація неповністю визначених логічних функцій.
- •Розділ 5. Теорія графів.
- •1. Основні поняття.
- •2. Способи задання графів.
- •3. Маршрути, ланцюги, цикли.
- •4. Ейлерів граф.
- •5. Дерево.
- •Чотирикутники
- •6. Транспортні мережі.
- •1. Поняття алгоритму.
- •2.Основні вимоги до алгоритмів.
- •3. Властивості алгоритмів.
- •4. Машина Тьюринга.
2. Основні логічні операції.
Означення логічних функцій дає можливість встановити істинність складного висловлення за значенням істинності його компонентів (складових).
Логічні операції застосовують для об’єднання простих висловлень у складні.
Основні логічні операції над висловленнями:
1) Операція „Константа – нуль ” – передає висловлення, яке завжди хибне: „F=0”.
Приклад:
А![]() „15
„15![]() 2”
– хибне завжди.
2”
– хибне завжди.
2) Операція „Константа – одиниця ” – передає висловлення, яке є завжди істинним: „F=1”.
Приклад:
В![]() „5<6” – істинне.
„5<6” – істинне.
3) Логічна операція: “Змінна А” - складне висловлення , яке істинне тоді, коли А - істинне і хибне, коли А – хибне.
4) Логічна операція „ Не” (заперечення) – це висловлення яке позначається „F=Ā”
і визначається таблицею істинності:
-
А
Ā
1
0
0
1
F = Ā – істинне тоді, коли А – хибне і навпаки.
Приклад:
а)
А
![]() ”5
”5![]() 3”
3”
![]() А=0
А=0
Ā
– означає: неправильно що 5![]() 3,
або „5
не ділиться на 3”,
тоді Ā=1
3,
або „5
не ділиться на 3”,
тоді Ā=1
б)
В![]() ”7
-
просте число ” В
”7
-
просте число ” В![]() 1,
тоді
1,
тоді
![]()
![]() 0
означає „неправильно, що 7
-
просте число”, або „7
–
непросте число”.
0
означає „неправильно, що 7
-
просте число”, або „7
–
непросте число”.
З
операцією заперечення зв’язана
тотожність:
![]()
![]() - закон подвійного заперечення.
- закон подвійного заперечення.
Тепер перейдемо до бінарних логічних операцій (операцій, які застосовуються до пари висловлень)
5)
Логічна операція «Кон’юнкція»(добуток,
логічне множення)- називається складне
висловлення F=А![]() В,
яке
істинне тоді і тільки тоді, коли
істинні обидва висловлення і А
і В.
В,
яке
істинне тоді і тільки тоді, коли
істинні обидва висловлення і А
і В.
-
А
В
А
 В
В0
0
1
1
0
1
0
1
0
0
0
1
Кон’юнкція відповідає союзу „і” і має конструкцію „… і ***”.
Кон’юнкція має слідуючи властивості:
-
 -
комутативний закон.
-
комутативний закон. -
 -
закон ідемпотентності.
-
закон ідемпотентності. -
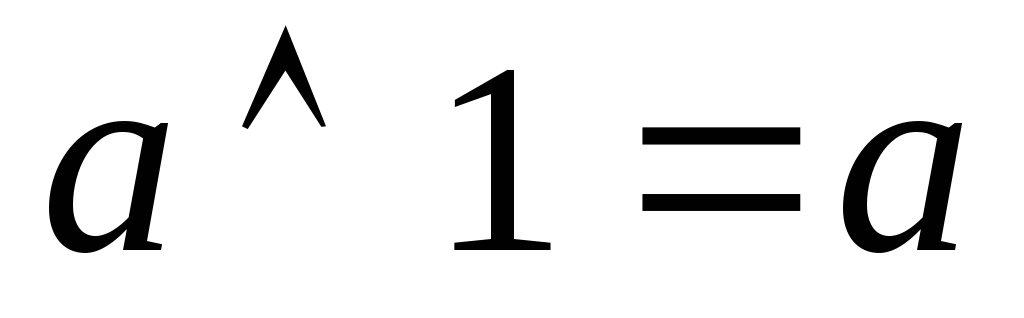
-
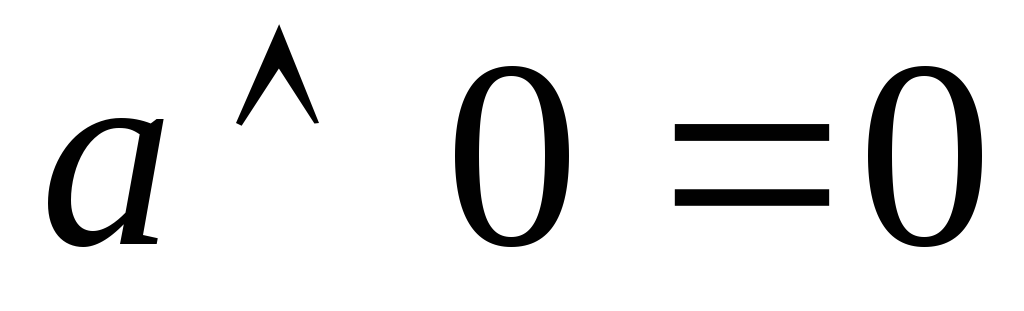
6)
Логічна операція «Диз’юнкція»
(логічна сума) –
називається
складне висловлення „![]() ”,
яке істинне тоді і тільки тоді коли
істинне хоча б одне із висловлень А
і В.
”,
яке істинне тоді і тільки тоді коли
істинне хоча б одне із висловлень А
і В.
Диз’юнкція відповідає сполучнику „або” і має конструкцію „… або ***”.
-
А
В

0
0
1
1
0
1
0
1
0
1
1
1
Властивості диз’юнкції.
-
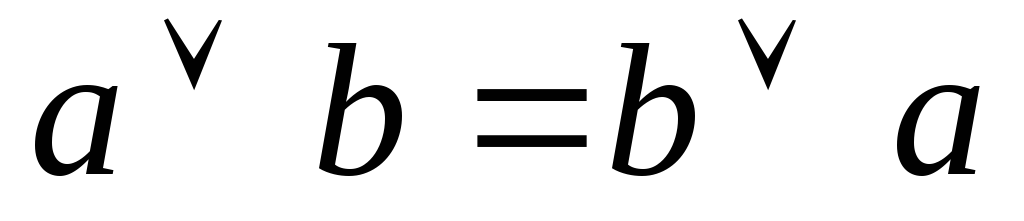 -
комутативний закон
-
комутативний закон -
 -
закон ідемпотентності
-
закон ідемпотентності -
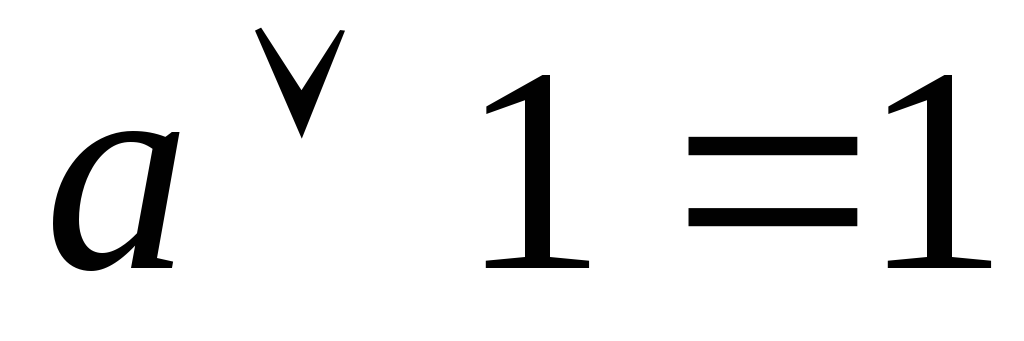
-
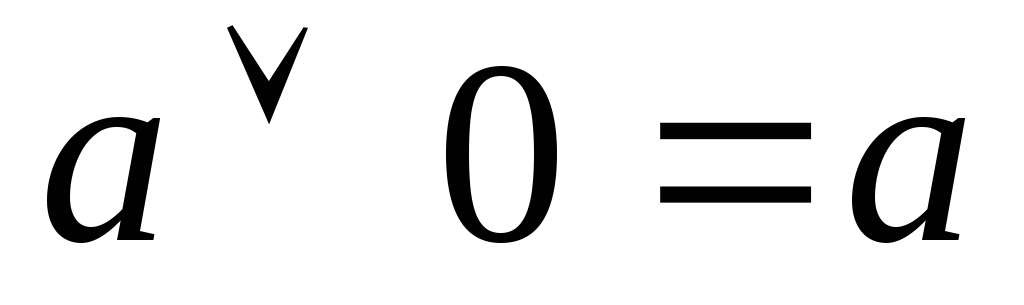
7)
Логічна операція „Імплікація”,
(„якщо-то”)
– називається складне висловлення
„![]() ”,
яке є хибним тоді і тільки тоді, коли А
– істинне, В
– хибне.
”,
яке є хибним тоді і тільки тоді, коли А
– істинне, В
– хибне.
Читається: „якщо А, то В” або „з А слідує В”.
А – називається умовою імплікації, В – наслідком
-
А
В

0
0
1
1
0
1
0
1
1
1
0
1
Приклад:
А![]() „36
„36![]() 24”
А = 0
24”
А = 0
В![]() „36
„36![]() 6”
В = 1
6”
В = 1
А
![]() В
В
![]() „Якщо 36
„Якщо 36![]() 24,
то 36
24,
то 36![]() 6”
6”
![]() 1
1
В
![]() А
А
![]() „Якщо 36
„Якщо 36![]() 6,
то 36
6,
то 36![]() 24”
24”
![]() 0
0
Для імплікації мають місце властивості:
1)(
а
![]() в)
в)
![]() (
в
(
в
![]() а)
4) 1
а)
4) 1
![]() а
а
![]() а
а
2)
а
![]() а
а
![]() 1
5) а
1
5) а
![]() 1
1
![]() 1
1
3)
0
![]() а
а
![]() 1
6) а
1
6) а
![]() 0
0
![]()
![]()
8)
Логічна операція: „Заборона
по В”
(заперечення імплікації А![]() В)
- називається складне висловлення „
В)
- називається складне висловлення „![]() ”,
яке є істинним тоді і тільки тоді, коли
А
– істинне, а В
– хибне
”,
яке є істинним тоді і тільки тоді, коли
А
– істинне, а В
– хибне
-
А
В
А Δ В
0
0
1
1
0
1
0
1
0
0
1
0
Читається: „Невірно, що якщо А то В»
9)
Логічна операція: „Заборона
по А”
(заперечення імплікації В![]() А)
називається складне висловлення „
А)
називається складне висловлення „![]() ”,
яке є істинним тоді і тільки тоді, коли
В
- істинне, а А
– хибне.
”,
яке є істинним тоді і тільки тоді, коли
В
- істинне, а А
– хибне.
-
В
А
ВΔА
0
0
1
1
0
1
0
1
0
0
1
0
10)
Логічна
операція:
“Еквівалентність”
(рівнозначність) - називається
складне
висловлення
„![]() ”,
(„
”,
(„![]() ”)
істинне тоді і тільки тоді, коли А=В=1
або А=В=0.
”)
істинне тоді і тільки тоді, коли А=В=1
або А=В=0.
-
А
В
А ~ В
0
0
1
1
0
1
0
1
1
0
0
1
Еквівалентність відповідає конструкції: „...рівносильно...” або „...тоді і тільки тоді, коли...”.
Властивості еквівалентності:
-
а ~ в
 в ~ а
–комутативний закон.
в ~ а
–комутативний закон. -
а ~ в
 ~
~
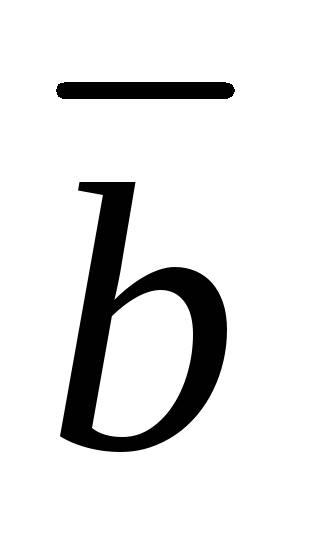
-
а ~ 1
 а
а -
а ~ 0

11)
Логічна
операція:
“Нерівнозначність”
-
складне
висловлення
F
=А![]() В
(А
В
(А![]() В),
яке істинне тоді і тільки тоді, коли
одне істинне, а друге хибне.
В),
яке істинне тоді і тільки тоді, коли
одне істинне, а друге хибне.
Читається: „А нерівнозначне до В”.
-
А
В
А
 В
В0
0
1
1
0
1
0
1
0
1
1
0
12)
Логічна операція: “Стрілка
Пірса” (функція
Вебба)
-
складне
висловлення,
яке істинне тоді і тільки тоді, коли
обидва висловлення А
і В
хибні: F=![]() =А
=А![]() В.
В.
Читається: „ні А ні В”.
-
А
В
А
 В
В0
0
1
1
0
1
0
1
1
0
0
0
13)
Логічна операція: “Штрих
Шефера” -
складне
висловлення
F=А│В=![]() ,
яке хибне тоді і тільки тоді, коли обидва
висловлення істинні.
,
яке хибне тоді і тільки тоді, коли обидва
висловлення істинні.
Читається: „невірно, що А і В”.
-
А
В
А│В
0
0
1
1
0
1
0
1
1
1
1
0
