
- •Розділ 1. Теорія множин.
- •1. Основні означення теорії множин.
- •2. Дії над множинами.
- •3. Алгебра множин.
- •Розділ 2. Вектори, відношення, відображення.
- •1. Вектори і прямий добуток множин.
- •2. Відношення.
- •Відображення.
- •4. Функції.
- •5. Перетворення.
- •6. Сукупність підстановок множини м: s(м).
- •7. Алгебраїчні операції та системи.
- •Розділ 3. Алгебра логіки.
- •1. Висловлення.
- •2. Основні логічні операції.
- •3. Основні закони алгебри логіки.
- •4. Логічна функція.
- •5. Бульові функції.
- •Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми.
- •1. Диз’юнктивні нормальні форми.
- •1) Елементарний добуток
- •2) Диз`юнкція різних елементарних добутків відносно
- •3) Тотожна хибність.
- •2. Досконала диз’юнктивна нормальна форма. (дднф)
- •3. Скорочена днф.
- •1. Імпліканта.
- •2. Скорочена днф.
- •4. Мінімізація логічних функцій методом Квайна.
- •5. Кон’юнктивні нормальні форми.
- •6. Мінімізація логічних функцій за допомогою таблиць Вейча.
- •7. Мінімізація неповністю визначених логічних функцій.
- •Розділ 5. Теорія графів.
- •1. Основні поняття.
- •2. Способи задання графів.
- •3. Маршрути, ланцюги, цикли.
- •4. Ейлерів граф.
- •5. Дерево.
- •Чотирикутники
- •6. Транспортні мережі.
- •1. Поняття алгоритму.
- •2.Основні вимоги до алгоритмів.
- •3. Властивості алгоритмів.
- •4. Машина Тьюринга.
6. Сукупність підстановок множини м: s(м).
Розглянемо
множину
![]() .
Підстановками на множині М будуть
.
Підстановками на множині М будуть
![]()
![]()
![]()
![]()
![]()
![]()
Підстановки
![]() і
і
![]() - рівні, бо в них область визначення
(елементи 1,2,3)
одна і та ж, і кожний елемент з області
визначення ці підстановки переводить
в одні і ті ж елементи: 1→1,
2→3, 3→2.
- рівні, бо в них область визначення
(елементи 1,2,3)
одна і та ж, і кожний елемент з області
визначення ці підстановки переводить
в одні і ті ж елементи: 1→1,
2→3, 3→2.
Цю властивість: переводити елементи з області визначення в одні і ті ж елементи, використовують при послідовному виконанні перетворень, яке називається композицією або добутком підстановок.
-
Покажемо, що добуток підстановок належить сукупності підстановок
![]()
Отже,
якщо
![]() і
і
![]() ,
то
,
то
![]()
-
Перевіримо чи виконується асоціативний закон для множення підстановок
![]() ?
?
![]()
![]()
![]()
![]() Отже,
асоціативний закон виконується.
Отже,
асоціативний закон виконується.
-
Перевіримо що буде, якщо
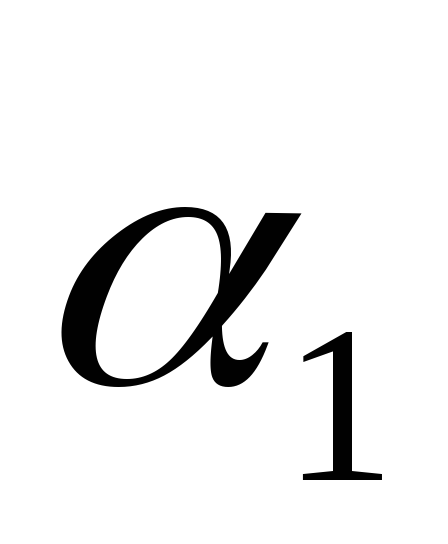 множити на будь-яку підстановку з
множини М.
множити на будь-яку підстановку з
множини М.
![]()
![]()
Висновок:
![]() - виступає одиничним елементом в
сукупності підстановок множини
- виступає одиничним елементом в
сукупності підстановок множини
![]() .
.
![]()
-
Знайдемо добуток:

![]()
![]()
Отже
![]()
7. Алгебраїчні операції та системи.
Операцією на множині М називається відповідність, при якій з кожною парою елементів з множини М зіставлений певний елемент цієї ж множини.
Означена таким способом операція може бути множенням або додаванням і записують. а ·b= c, а + b = c.
Приклад: Дія додавання ставить у відповідність парі чисел 2 і 3 число 5.
( 2; 3) → 5
Операція називається асоціативною для множення і додавання, якщо для будь-яких а, b, c є М виконується співвідношення.
![]()
![]()
Якщо
операція довільна і парі
![]() елементів з М
вона ставить у відповідність елемент
с,
то коротко це записують так:
елементів з М
вона ставить у відповідність елемент
с,
то коротко це записують так:
![]() .
Елемент с
називають композицією.
.
Елемент с
називають композицією.
Напівгрупа.
Множина М із заданою на ній дією ◦ називається напівгрупою, якщо
-
для кожних
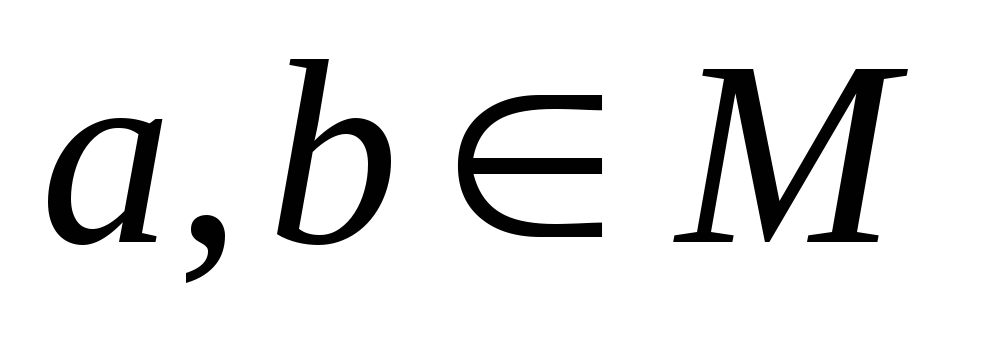 ,
композиція
,
композиція
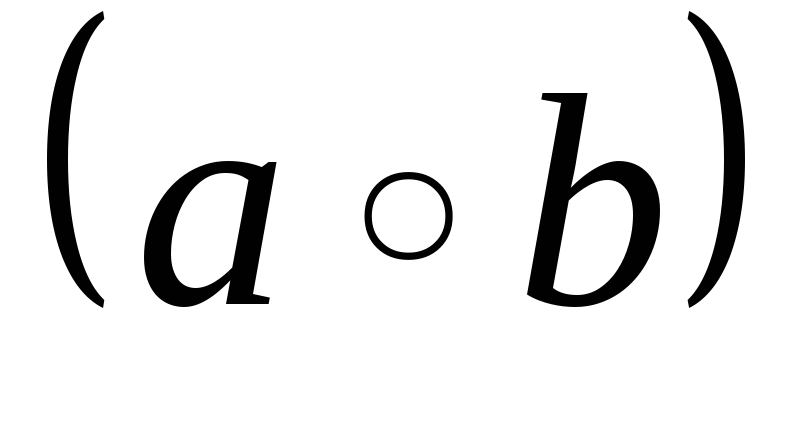 теж належить М;
теж належить М; -
дія ◦, задана на М, асоціативна: тобто для кожних елементів
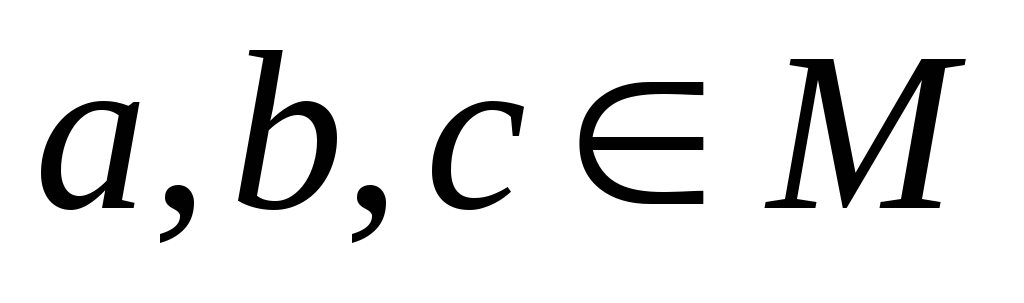 виконується рівність
виконується рівність
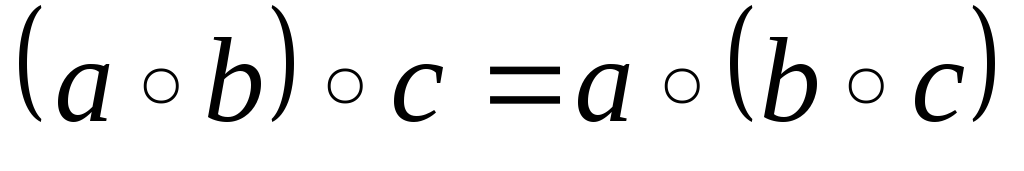 ;
; -
існує такий елемент
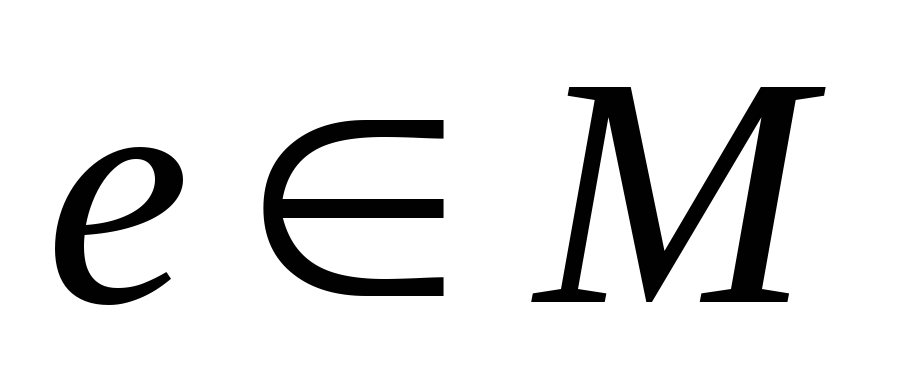 ,
що для кожного
,
що для кожного
 маємо
маємо
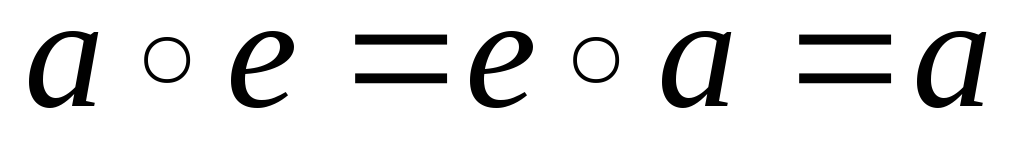
Елемент e – називається нейтральним для дії ◦; для „+” е – називається нульовим; для „·” – е називається одиничним елементом.
Приклади.
-
Множина Z – цілих чисел, відносно дії „+” – напівтрупа.
-
Множина Z цілих чисел, відносно дії множення є напівтрупа.
-
Сукупність підстановок множини М: S(M) – є напівгрупою відносно множення.
-
Множина Z+ додатних цілих чисел із заданою операцією
 не є напівгрупою.
не є напівгрупою.
Група.
Множина М із заданою на ній операцією називається групою, якщо
-
для будь-яких
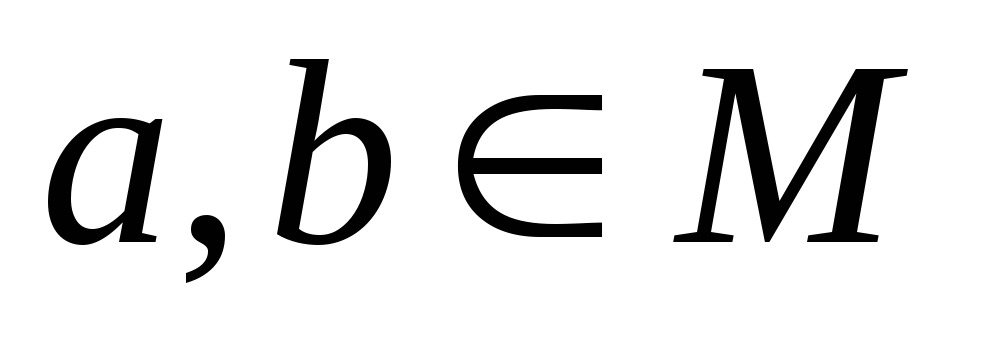 ,
композиція
,
композиція
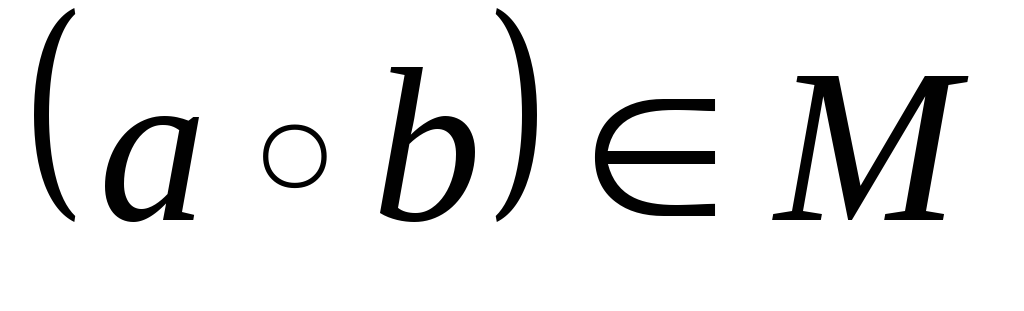
-
дія ◦ задана на М – асоціативна:
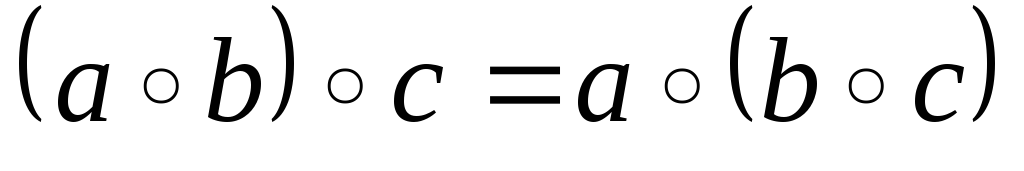
-
існує нейтральний елемент е:
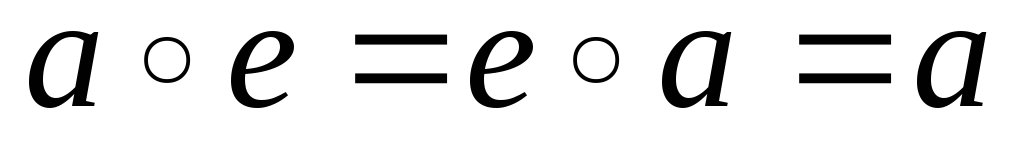
-
для кожного
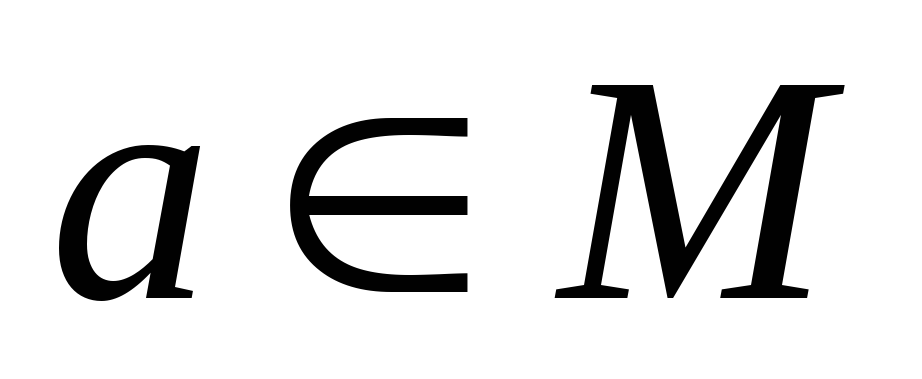 існує такий елемент
існує такий елемент
 ,
що
,
що
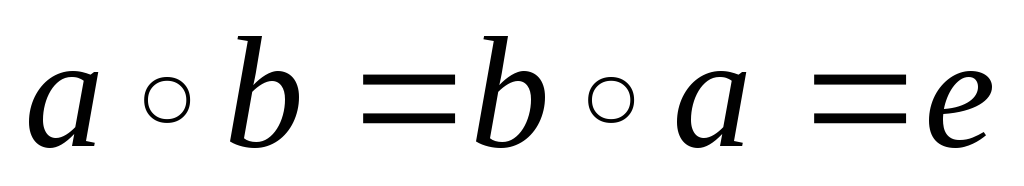
Зауваження:
-
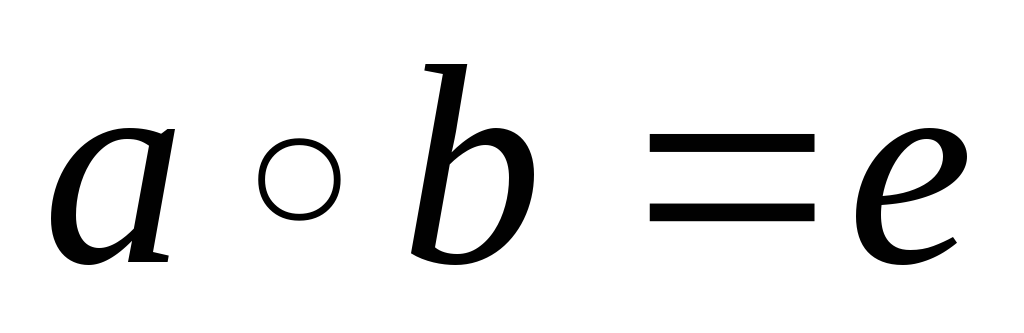 ,
то для дії „+” -
b
називається протилежним: а
і –а
(бо
а+(-а)=0
),
бо їх сума дорівнює нейтральному
елементу – 0.
,
то для дії „+” -
b
називається протилежним: а
і –а
(бо
а+(-а)=0
),
бо їх сума дорівнює нейтральному
елементу – 0.
-
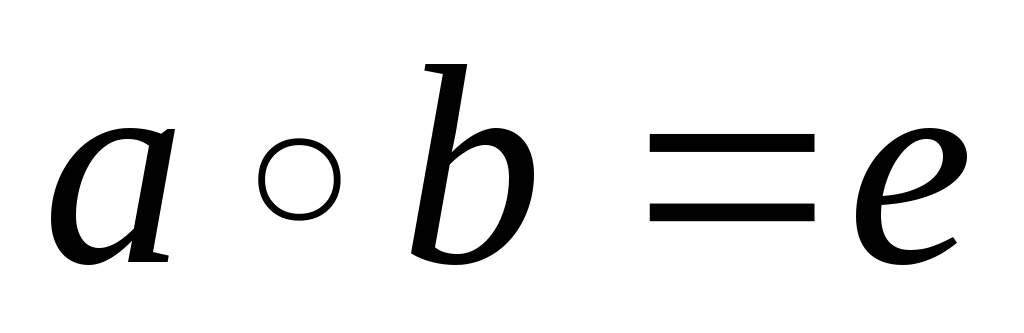 для
дії „·”
b
називається оберненим елементом
для
дії „·”
b
називається оберненим елементом
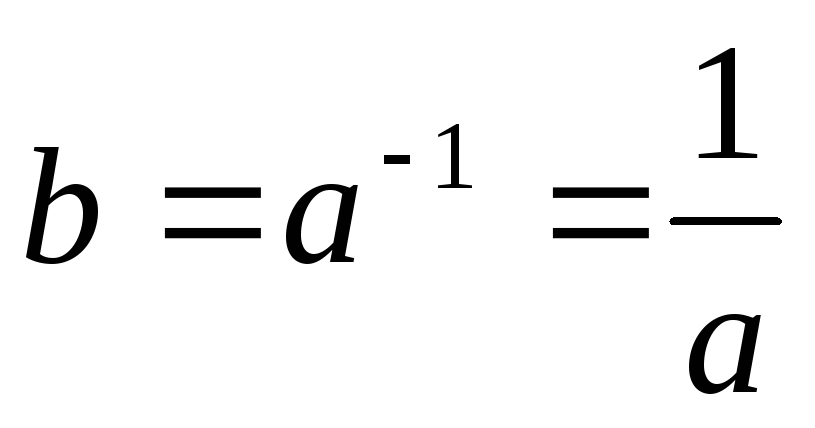 ,
бо
,
бо
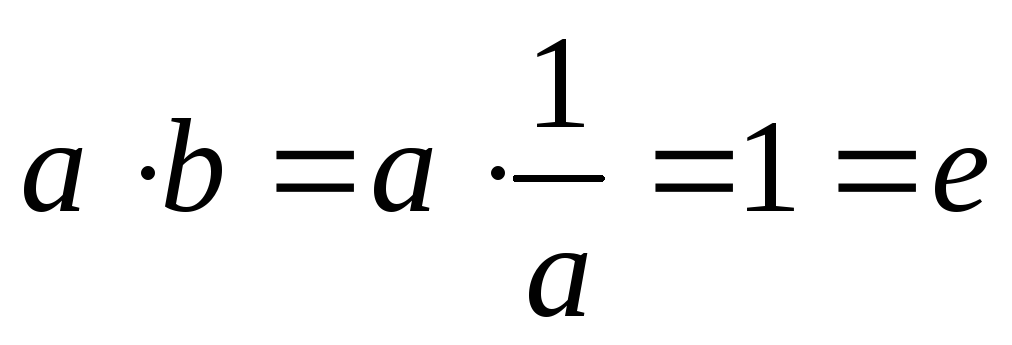 - одиничному елементу.
- одиничному елементу.
Приклади:
-
Множина Z усіх цілих чисел є група.
-
Множина R+ додатних дійсних чисел відносно множення є група.
-
S(M) – сукупність підстановок множини М є група.
-
Числа -1 і 1 утворюють групу з операцією множення.
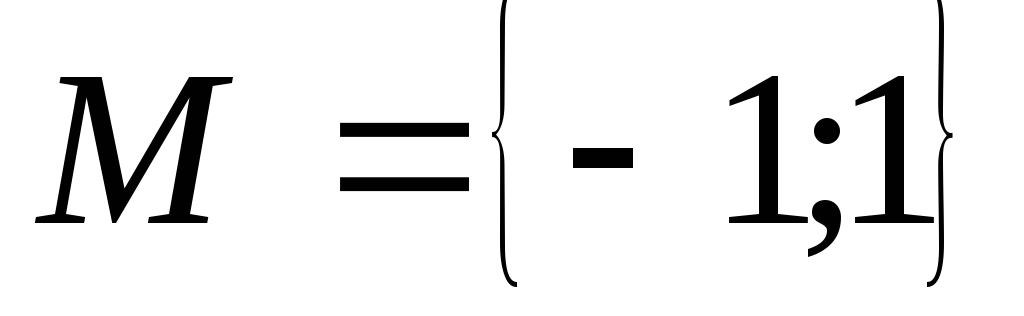
Кожна група є напівгрупою, але не навпаки.
Дії „+” і „·” чисел мають властивості комутативності. Але вимога комутативності не входить до означення групи і напівгрупи. Це пояснюється тим, що дія множення перетворень не комутативна, а історичне поняття групи виникло саме на основі вивчення властивості дії множення підстановок.
Група, для якої виконується умова комутативності називається абелевою.
Якщо,
між елементами двох груп встановлена
взаємно-однозначна відповідність, при
якій для будь-яких
![]() і відповідних їм елементів
і відповідних їм елементів
![]() елементу
елементу
![]() відповідає елемент
відповідає елемент
![]() ,
то такі групи називаються ізоморфними.
,
то такі групи називаються ізоморфними.
Ізоморфні групи можуть відрізнятися одна від одної лише природою своїх елементів, але всі властивості ізоморфних груп однакові.
Множина М називається кільцем, якщо на ній визначені одразу дві операції „+” і „·”, причому
-
операція „+” - комутативна
-
операції „+” і „◦” зв’язані дистрибутивними законами:
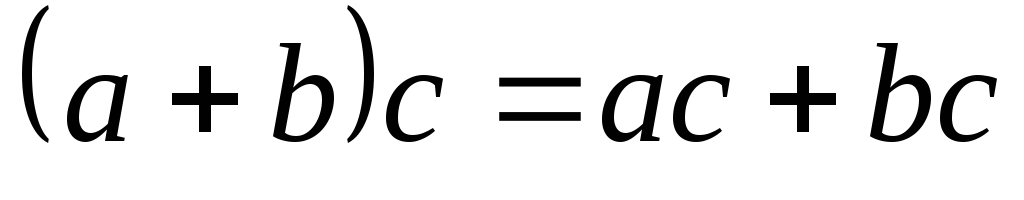 ,
,
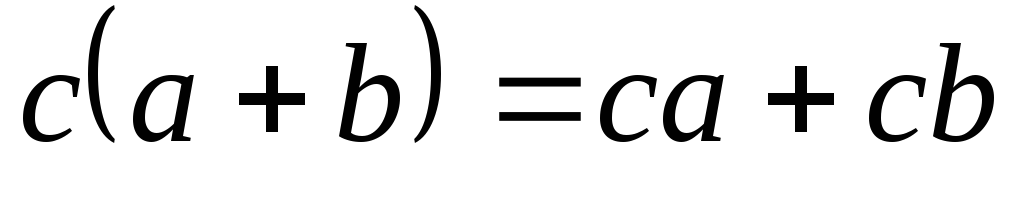
У кільці може не бути одиниці і обернених елементів.
Приклади:
-
Множина Z цілих чисел кільце відносно „+” і „·”
-
Множина раціональних чисел Q – кільце відносно „+” і „·”.
Якщо
в кільці для будь-якого
![]() і будь-якого
і будь-якого
![]() існує рівно один елемент
існує рівно один елемент
![]() такий, що
такий, що
![]() ,
то таке кільце називається полем,
а елемент
,
то таке кільце називається полем,
а елемент
![]() називається часткою від ділення
називається часткою від ділення
![]() на
на
![]() і позначається
і позначається
![]() .
.
Кільця
раціональних чисел Q та дійсних чисел
R
є полями, бо для будь-якого
![]() і будь-якого
і будь-якого
![]() знайдеться таке число
знайдеться таке число
![]() ,
що
,
що
![]() .
.
![]()
![]() ,
тоді
,
тоді
![]()
Перейдемо до більш широкого розкриття змісту поняття групи, бо група є одним з найбільш важливих об’єктів дискретної математики.
В загальній теорії група визначається як множина елементів G із заданою на ній двомісною (бінарною) операцією f, що задовольняє певним умовам.
Ця
операція називається груповою
операцією (або груповим
законом) (операція f
відображає будь-яку пару елементів
![]() в елемент цієї ж множини).
в елемент цієї ж множини).
Групова операція – це функція, що перетворює будь-яку пару елементів множини G у деякий елемент тієї самої множини.
При цьому обов’язково зазначають який елемент перший, а який другий. групову операцію позначають +, · або ◦.
Групою називається пара < G;f >, яка складається з множини елементів G і двомісної операції f над ними, якщо ця операція задовольняє умовам:
-
операція f асоціативна:
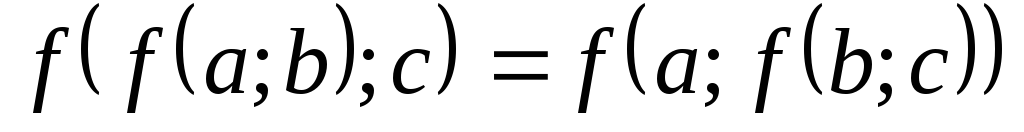
-
існує нейтральний елемент (елемент е множини G, що для будь-яких
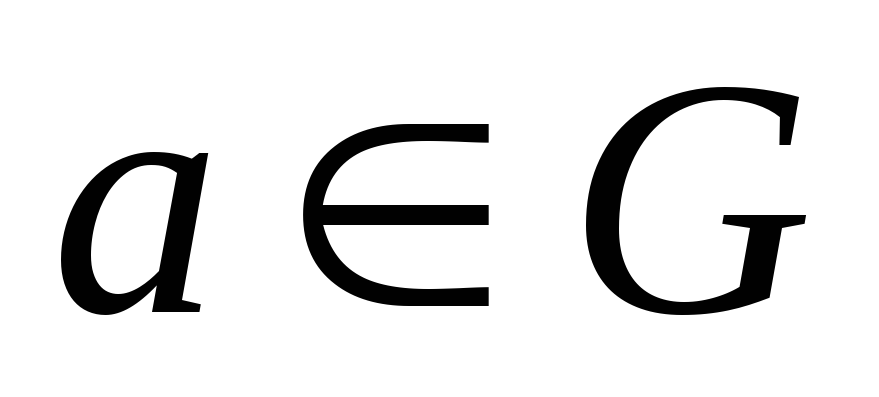 :
:
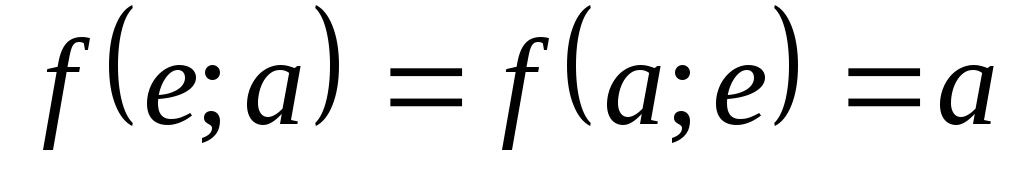 )
) -
існує зворотній елемент (тобто для будь-яких
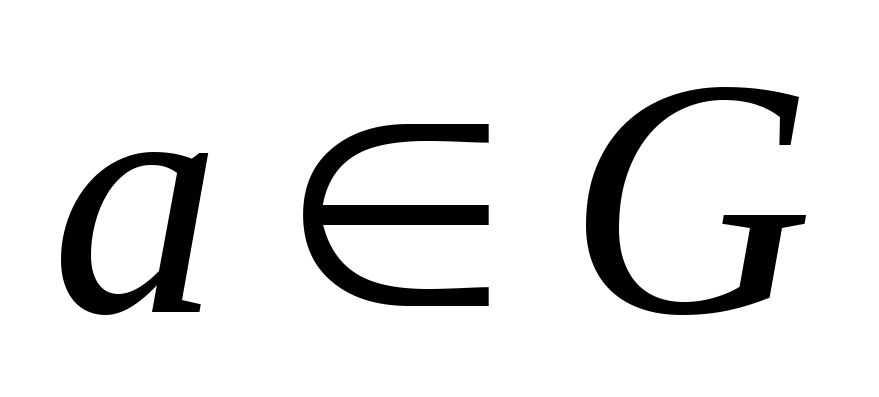 можна знайти свій
можна знайти свій
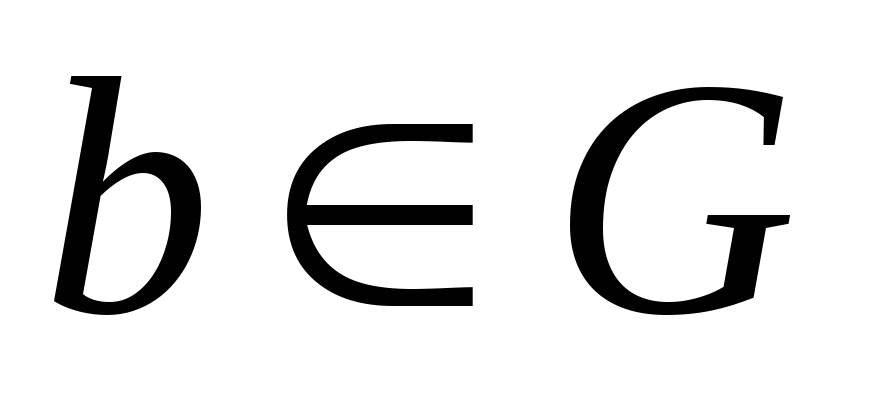 такий, що
такий, що
 )
)
Елементи множини G називаються елементами групи.
Умови 1, 2, 3 – називаються аксіомами (первинними істинами).
Якщо у групі визначена групова операція „·”, то вона називається мультиплікативною.
Якщо у групі визначена групова операція „+”, то така група називається адитивною.
Група називається скінченною, якщо у ній скінченна кількість елементів.
Група називається нескінченною, якщо у ній нескінченна кількість елементів.
Кількість елементів скінченної групи називається порядком.
Аксіома асоціативності встановлює порядок перемноження трьох співмножників a, b, c, який може здійснюватись або зліва направо, але за раз заданим порядком. Співмножники, що стоять поряд перемножуються в першу чергу. Потім здійснюється перемноження одержаного результату із співмножником, що залишився. При цьому треба дотримуватись встановленого порядку перемноження, бо результати множення зліва направо і справа наліво можуть відрізнятись.
Приклади груп:
-
число 0 утворює групу за множенням і додаванням: G = {0; +; ·}
-
число 1 утворює групу за множенням G = {1; ·}
Контрольні запитання.
-
Що таке кортеж?.
-
Що називається довжиною кортежу?
-
Який кортеж називається порожнім?
-
Що називається прямим добутком множин?
-
Що таке відношення?
-
Які є способи задання відношень? (*)
-
Яке відношення називається оберненим?
-
Сформулювати властивості відношень. (*)
-
Що називається відображенням множини А в множину В?
-
Способи задання відображень.(*)
-
Які є види відображень? Їх особливості. (**)
-
Яке відображення називається функцією?
-
Способи задання функції?
-
Що називається перетворенням?
-
Які є види перетворень?
-
Що називається напівгрупою? Наведіть приклади. (**)
-
Що називається групою? Наведіть приклади. (**)
-
Які групи називаються ізоморфними?
-
Яка множина називається кільцем?
-
Що називається полем?
Література:
О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 5 - 9
Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.12 – 1.13, розділ 5. п.5.1 - 5.2, 5.5
