3. Маршрути, ланцюги, цикли.

Нехай G - неорієнтований граф.

Маршрутом у графі називається скінченна або нескінченна послідовність ребер () така, що кожні два сусідні ребра мають спільну інцидентну вершину.

Одне і теж ребро може зустрічатись в маршруті декілька разів.

Якщо маршрут скінчений, то в ньому є початкове і кінцеве ребро .

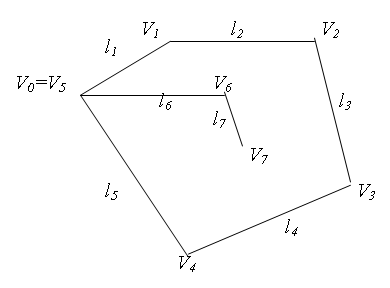
Вершина – інцидентна ребру і не інцидентна ребру називається початком маршруту. Вершини маршруту, які не є початком і кінцем називаються внутрішніми вершинами.

Якщо ребра і кратні, то необхідна спеціальна вказівка, яку з двох інцидент них їм вершин вважати початком маршруту. Так як різні ребра маршруту можуть бути інцидентними одній і тій же вершині ( інцидентні вершині ), то початок або кінець маршруту можуть одноразово виявитись внутрішньою вершиною.

Нехай маршрут має початок у вершині і кінець у вершині , тоді М називають маршрутом, з’єднуючим вершини і .

Кількість ребер маршруту називають його довжиною.

Якщо початок і кінець маршруту співпадають, то маршрут називається циклічним.

Відрізок скінченого або нескінченного маршруту називається ділянкою маршруту.

Якщо в маршруті кожне ребро зустрічається не більше одного разу, то такий маршрут називається ланцюгом.

Якщо кожна вершина графа інцидентна не більш ніж двом ребрам графа, то такий маршрут називається простим ланцюгом.

Циклічний маршрут називається циклом, якщо він є ланцюгом.

Маршрут, який є простим ланцюгом називається простим циклом.

Цикл, який містить всі ребра графа називається обходом графа.

Обхід, при якому кожне ребро графа проходиться рівно один раз називається правильним.

4. Ейлерів граф.

Граф, який допускає правильний обхід називається Ейлеровим.

Народженням теорії графів ми зобов’язані постановці та розв’язанню задачі Леонардом Ейлером про розташування мостів у місті Кенігсберзі в часи його життя.

Задача, яку він розв’язував формулюється так:

якщо вийти з деякої частини міста, то чи можна пройти кожен міст один раз і повернутися в початкову частину міста.

Можна побудувати граф задачі, в якому кожній частині міста відповідає вершина, а кожному мосту відповідає ребро, інцидентне вершинам, що стосуються тих частин міста, які з’єднуються цим мостом.

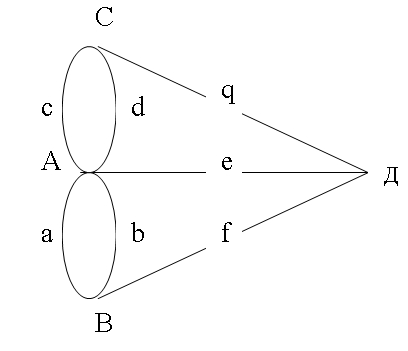
Обходу мостів відповідає послідовність ребер графа задачі, в якій два сусідні ребра мають спільну вершину, тобто маршрут. Так як в кінці обходу треба повернутися в початкову вершину міста і на кожному мості побувати один раз, то цей маршрут є циклом, що містить усі ребра графа.

Можна сказати, що Ейлерові графи це такі графи, які можна зобразити одним розчерком пера, при чому процес його зображення починається і закінчується в тій самій точці. Леонард Ейлер розв’язав цю задачу.

Теорема Ейлера: скінчений неорієнтований граф є Ейлеровим тоді і тільки тоді, коли він зв’язний і степені всіх його вершин парні.

Граф називається зв’язним, якщо будь – які дві вершини з’єднані маршрутом.

Будь – який не зв’язний граф складається з кількох частин, кожна з яких є зв’язним графом. Ці частини називаються компонентами зв’язності графа.

Дві вершини називаються зв’язними, якщо існує маршрут з кінцями в цих вершинах.

У даній задачі вершини А, В, С, Д мають непарні степені, тому розв’язання задачі неможливе.