
- •Розділ 1. Теорія множин.
- •1. Основні означення теорії множин.
- •2. Дії над множинами.
- •3. Алгебра множин.
- •Розділ 2. Вектори, відношення, відображення.
- •1. Вектори і прямий добуток множин.
- •2. Відношення.
- •Відображення.
- •4. Функції.
- •5. Перетворення.
- •6. Сукупність підстановок множини м: s(м).
- •7. Алгебраїчні операції та системи.
- •Розділ 3. Алгебра логіки.
- •1. Висловлення.
- •2. Основні логічні операції.
- •3. Основні закони алгебри логіки.
- •4. Логічна функція.
- •5. Бульові функції.
- •Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми.
- •1. Диз’юнктивні нормальні форми.
- •1) Елементарний добуток
- •2) Диз`юнкція різних елементарних добутків відносно
- •3) Тотожна хибність.
- •2. Досконала диз’юнктивна нормальна форма. (дднф)
- •3. Скорочена днф.
- •1. Імпліканта.
- •2. Скорочена днф.
- •4. Мінімізація логічних функцій методом Квайна.
- •5. Кон’юнктивні нормальні форми.
- •6. Мінімізація логічних функцій за допомогою таблиць Вейча.
- •7. Мінімізація неповністю визначених логічних функцій.
- •Розділ 5. Теорія графів.
- •1. Основні поняття.
- •2. Способи задання графів.
- •3. Маршрути, ланцюги, цикли.
- •4. Ейлерів граф.
- •5. Дерево.
- •Чотирикутники
- •6. Транспортні мережі.
- •1. Поняття алгоритму.
- •2.Основні вимоги до алгоритмів.
- •3. Властивості алгоритмів.
- •4. Машина Тьюринга.
Розділ 3. Алгебра логіки.
План.
-
Висловлення.
-
Основні логічні операції. (*)
-
Основні закони алгебри логіки. (**)
-
Логічні функції. (***)
-
Бульові функції. (***)
1. Висловлення.
Математична логіка – це алгебра висловлень, яка дає простий логічний апарат і відповідну символіку.
Свої судження і висновки в повсякденному житті люди передають за допомогою речень. Особливу роль відіграють речення стверджувальні і розповідні, які несуть інформацію і відносно яких можна поставити питання істинне воно чи хибне.
Приклади: 1) числа 9 і 37 взаємно-прості;
2) Архімед – англійський математик
Можна стверджувати, що приклад 1 є істинним висловленням, а приклад 2 – хибне.
Терміни „висловлення”, „істинне висловлення”, „хибне висловлення” належать до неозначуваних понять.
Висловлення вивчають тільки з точки зору того, істинні вони чи хибні, зовсім не цікавлячись їхнім конкретним змістом.
Висловлювання вважають своєрідною величиною, яке може мати тільки одне значення: „істинне” або „хибне”.
Висловлення – зв’язне розповідне речення, про яке модна сказати „істинне” воно або „хибне”.
Будь-яке твердження, що може бути істинним або хибним називається висловленням.
Приклади:
-
„2×2=4”
-
„2<3”
-
Річка Дон в 1998 році нашої ери впадає в Каспійське море.
-
„
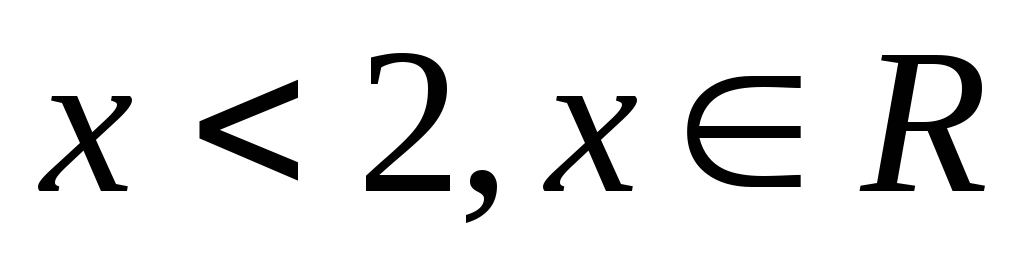 ”
,
„Дійсне число, менше 2”
”
,
„Дійсне число, менше 2” -
„Площа відрізка менша довжини куба”
-
Чи є х=3 коренем рівняння
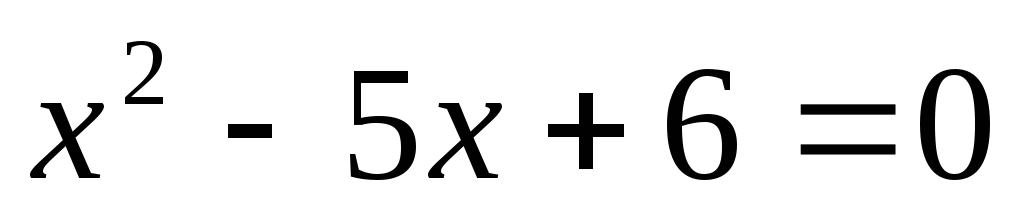 ?
? -
Менше один в являється два.
-
Слава російським студентам!
-
„
 ”
”
Висловленнями є приклади 1, 2, 3, 9. при чому 1 і 2 – істинні, а 3 і 9 – хибні.
Приклад 5 – не є висловленням, бо про нього не можна сказати істинне воно або хибне (за відсутністю змісту).
Приклад 4 – не є висловленням, бо в ньому є змінна, і через неї це речення має властивість перетворюватись в висловлення при фіксації змінної, якщо х= -1, то висловлення 4 – істинне висловлення, якщо х=3, то висловлення 4 – хибне висловлення. Такі приклади є узагальненими прикладами.
Приклади 6, 8 –не висловленнями, бо не є розповідними реченнями.
Приклад 5 – не висловлення, бо відсутній зміст розповідного речення.
Отже, висловлення можуть бути утворені за допомогою слів або символів, але далеко не кожний набір слів або символів є висловленням.
Висловлення позначають буквами латинського алфавіту: А,В,С...
![]() ,
,
![]() .
.
Знак
![]() заміняє слова „є висловленням”.
заміняє слова „є висловленням”.
Висловлення ділять на прості та складні.
Висловлення:
А
![]() „Вісім – парне число”
„Вісім – парне число”
В
![]() „Одинадцять ділиться на 3”
„Одинадцять ділиться на 3”
С
![]() „Київ – столиця України”
„Київ – столиця України”
Висловлення
А,
С
– істинні, їм приписується значення 1,
А![]() 1,
С
1,
С![]() 1.
1.
Висловлення
В
– хибне; В![]() 0,
приписують значення рівне 0.
0,
приписують значення рівне 0.
З простих висловлень при допомозі так званих логічних зв’язок (союзів „і”, „або”, слів: „якщо..., то...”, „тоді і тільки тоді, коли...”) можна утворювати нові висловлювання які називаються складними:
Приклад:
Висловлення
![]() ;
і В
;
і В![]() „число 6 – просте ” – прості.
„число 6 – просте ” – прості.
З висловів А і В можна утворювати слідуючи складні висловлення:
С
![]() „6<7
або
6
– просте число”;
„6<7
або
6
– просте число”;
D
![]() „6<7
і
число 6
–
просте ”;
„6<7
і
число 6
–
просте ”;
Е
![]() „6<7
тоді і тільки тоді, коли число 6
просте”;
„6<7
тоді і тільки тоді, коли число 6
просте”;
F
![]() „якщо
6<7,
то число 6
- просте ”.
„якщо
6<7,
то число 6
- просте ”.
Зауваження: нові висловлення можна утворювати з таких висловлень, які між собою ніяк не зв’язані по смислу.
Наприклад:
М![]() „Якщо слон – комаха, то Антарктида
покрита тропічними лісами”.
„Якщо слон – комаха, то Антарктида
покрита тропічними лісами”.
(висловлення М – складене за допомогою логічної зв’язки – „якщо..., то...” з двох висловлень, які між собою аж ніяк не зв’язані).
В математичній логіці істинність складного висловлення установлюється незалежно від істинності чи хибності простих висловлень з яких вони складені, а на основі зв’язок за допомогою яких вони складені.
