4. Функції.

Функцією називається відображення, що ставить у відповідність кожному елементу з області визначення єдиний елемент з області значень .

Елемент називається аргументом, - значенням функції на .

Функції і називаються рівними, якщо їх область визначення є одна і та сама множина .

Якщо область визначення функції складається з одного елемента, то функція називається функцією-константою.

Символ функції використовується у двох розуміннях:

1) - це множина, елементами якої є пари , які беруть участь у відношенні між множинами та .

2) - це означення для , що відповідає .

Формальне означення функції: .

Способи задання функції:

1) перерахуванням всіх пар у вигляді таблиці

х
у

2) у вигляді формули, що містить перелік математичних операцій, які мають бути виконані над , щоб отримати .

Якщо і , то .

Вираз, що містить функціональні знаки і символи аргументів називають формулою.

Якщо у виразі , , то будемо мати функцію від двох змінних і , яка позначається , де

Якщо і - дві функції: , , то оберненими до них є функції ,

Функція типу називається n-місною. Така функція має n аргументів і позначається , де , .

Композиція функцій і : о: , для кожного визначає

Більш загальним поняттям, ніж функція є поняття функціоналу.

Функціонал встановлює залежність між деякою множиною чисел і деякою множиною функцій (залежність числа від функції).

Наприклад: означений інтеграл , - функціонал – це число, що залежить від функції , яка обирається з деякої множини функцій.

Оператор – це більш загальне поняття. Він встановлює залежність між двома множинами функцій так, що кожній функції з однієї множини відповідає певна функція з другої множини.

Приклад: Р – оператор диференціювання, тоді зв’язок між похідною: і функцією може бути записаний у вигляді операторного співвідношення .

5. Перетворення.

Перетворення – це відображення множини самої на себе.

Табличний вигляд перетворення має вигляд 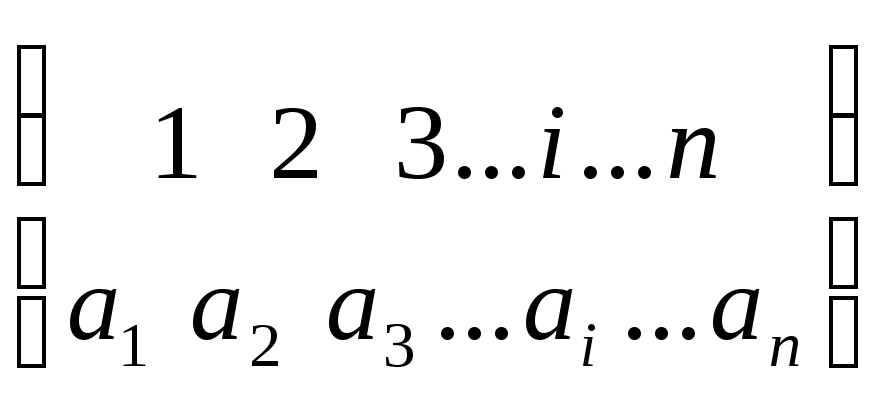де .

Приклад. Нехай задана множина

Для множини М можуть бути такі перетворення

а) б) в) та інші.

Деякі перетворення множини М мають спеціальну назву.

1. Тотожне перетворення – це перетворення множини М, при якому всі елементи з М залишаються на місці .

2. Постійне перетворення – це перетворення, при якому кожному елементу з множини М ставиться у відповідність деякий фіксований елемент цієї множини: .

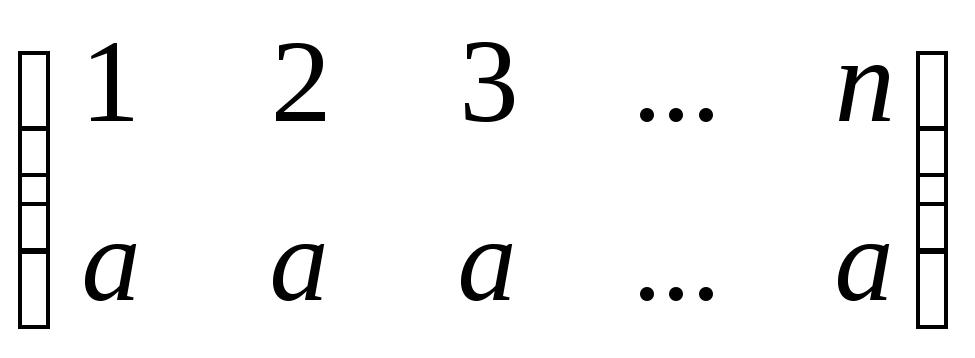
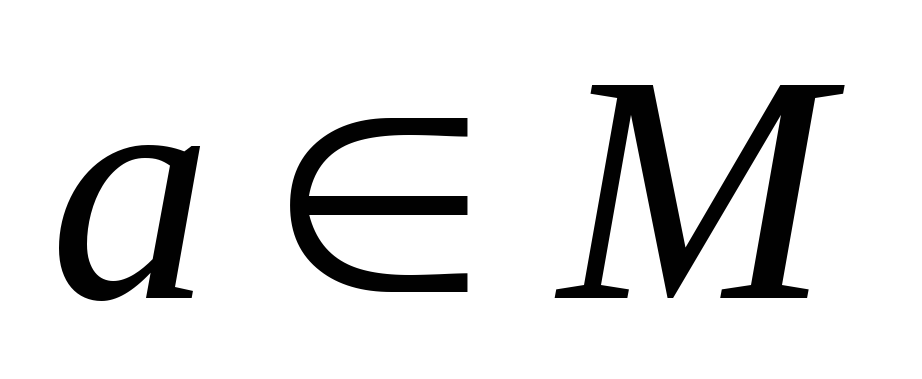3. Підстановка – це бієкція множини М на себе. 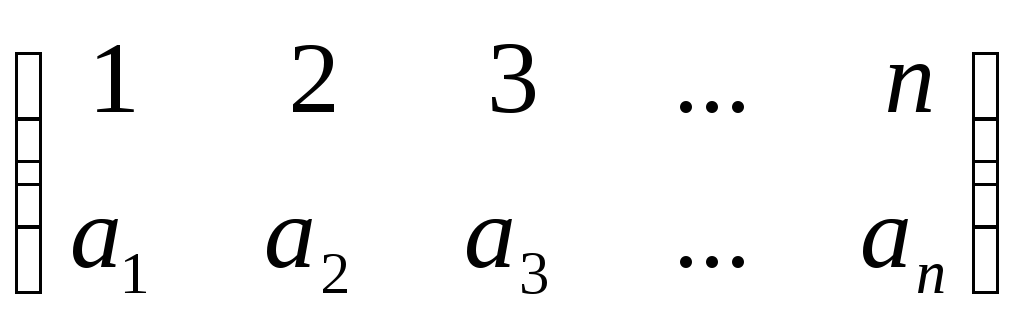, де , ,

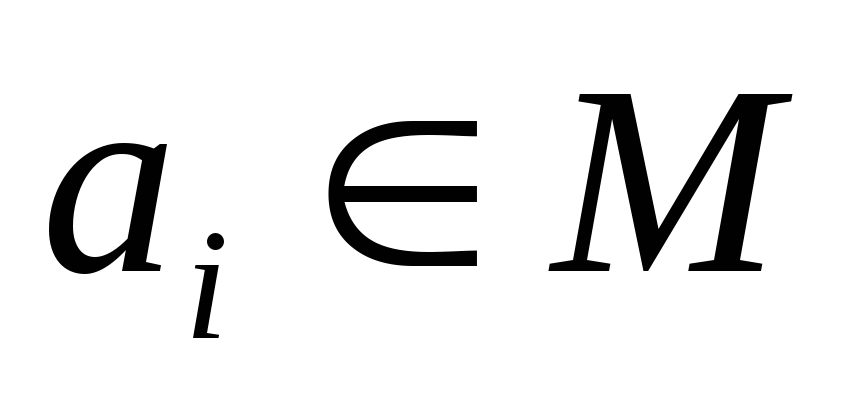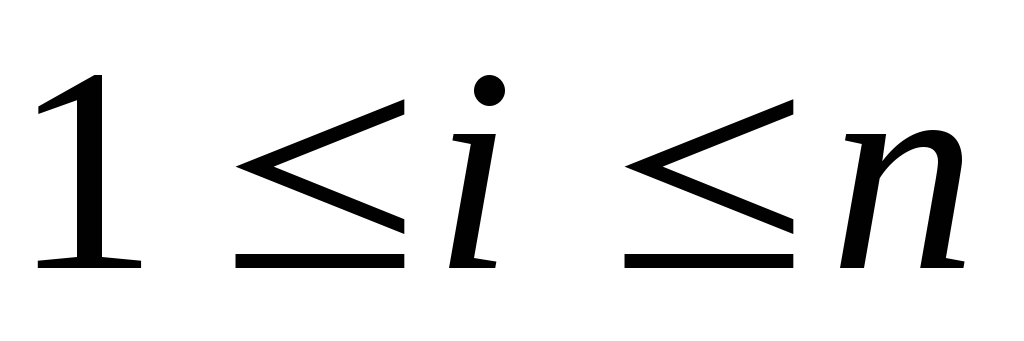
Композицією перетворень φ і ψ називається таке перетворення ω, який кожний елемент перетворює в образ , а потім в : :

Приклад. Нехай φ: х→х+3 – перетворення множини дійсних чисел R, яке числу х ставить у відповідність число х+3, а ψ: х → х+2, тоді перетворення ώ є композиція , яка кожне число х переводить у х+5: х → х+5.

φ: х → х+3

ψ: х → х+2

ω: φ ◦ ψ: x → x+5

Якщо х=3, то φ ◦ ψ: 3 → 8